python初心者がkaggleのHousePriceコンペに参加してみた

#はじめに
kaggleというコンペサイトの「HousePrice」というコンペに参加してみました。機械学習の勉強を初めて約１ヶ月なので至らないところばかりですが、結果から言うと
精度はtrainデータで93.8％、testデータで**92.4%**でした。
順位は 1302位/4146人
でした。
このコンペの概要を簡単に記しておくと、アメリカの不動産価格を予想する機械学習モデルを組み立てるというものです。変数名などはすべて英語です。
コードはgithubに載せておきます。

#分析の流れ
具体的な説明に入る前に、全体像を記します。

1.データの概要、外れ値の削除
2.前処理（欠損値処理と変数変換）
3.目的変数の分布の確認、処理
4.特徴量の選択
5.4つの学習インスタンスをグリッドサーチで作成
6.アンサンブル学習として、4つの結果の平均を取り、コンペに提出
7.結果まとめ

これを軸にしてQiitaの記事を書いていこうと思います。

1.データの確認

• まずデータを読み込んでshapeを確認します。

df_train=pd.read_csv('train.csv')
df_test=pd.read_csv('test.csv')
print(df_train.shape,df_test.shape)

(1456, 80) (1459, 79)

columnsから今回の特徴量は79個です。割と多いですね。

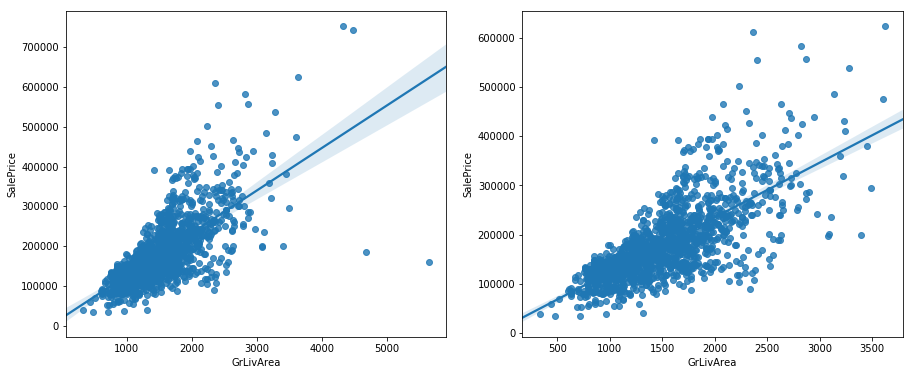
• 次に、欠損値処理を行います。これはコンペサイトの'Acknowlegement'のページに飛ぶと、このデータの提供元の論文で、「'GrLivArea'という特徴量が4000を超えるデータはおかしなデータなので分析する際には取り除いた方が良い。」とあるので、今回はそれに乗っ取り外れ値を削除します。

plt.subplot(1,2,1)
sns.regplot(x=df_train['GrLivArea'],y=df_train['SalePrice'])
plt.subplot(1,2,2)
df_train=df_train.drop(df_train[(df_train['GrLivArea']>4000)].index)
sns.regplot(x=df_train['GrLivArea'],y=df_train['SalePrice'])

左が処理前で右が処理後です。データのまとまりが良くなりました。

2.前処理

##2-0. 前処理で工夫したところ

• コンペサイトをよく読んで、外れ値削除の記述を見つけ、実行したこと(1へ)
• 変数の型ごとに欠損値補完を施したこと
• for文をうまく用いてmappingを行ったこと
• カテゴリデータの欠損値を0で洗わせたこと
• 目的変数SalePriceの分布を見て、log(x)を適用し、正規型にしたこと(3へ)

最初に目的変数'SalePrice'を分離しておきます。

#前処理のため目的変数priceをとりあえず分離
df_price=df['SalePrice']
df=df.drop('SalePrice',axis=1)

これから先の操作はtrainデータを用いて記しますが、後にtestデータでも同様の操作を行います。

2-1.欠損値の数、分布の確認

df_train.isnull().sum()[df_train.isnull().sum()>0].sort_values(ascending=False)

PoolQC 1451

MiscFeature     1402
Alley           1365
Fence           1176
FireplaceQu      690
LotFrontage      259
GarageYrBlt       81
GarageType        81
GarageFinish      81
GarageQual        81
GarageCond        81
BsmtFinType2      38
BsmtExposure      38
BsmtFinType1      37
BsmtCond          37
BsmtQual          37
MasVnrArea         8
MasVnrType         8
Electrical         1
dtype: int64

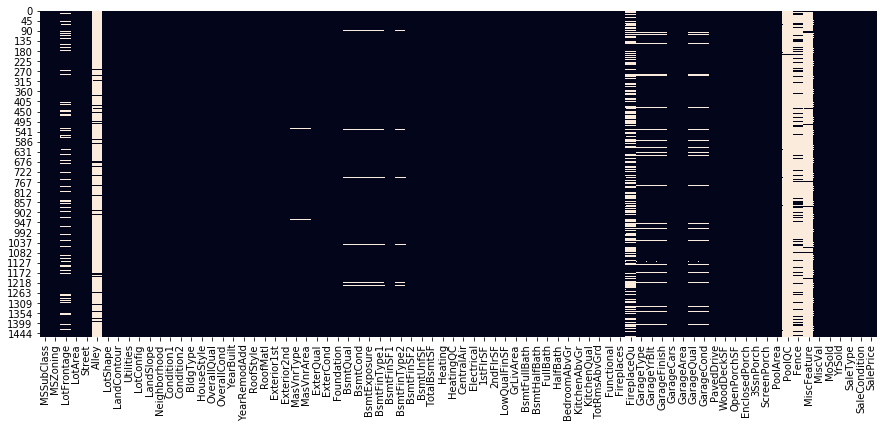
plt.figure(figsize=(15,6))
sns.heatmap(df_train.isnull(),cbar=False)

• 以上から、欠損の多すぎる特徴量があること、欠損の分布にも一定の相関があることがわかりました。

2-2. 欠損の多すぎる特徴量の削除

　'Alley'や'PoolQC'などの特徴量を削除します。
今回は基準として、欠損が2割未満のものだけ残します。(2割という数字は先の「特徴量ごとの欠損値の数」から導きました。)

##trainデータ前処理開始
df=df_train.copy()
#欠損値処理
a=0.2
b=len(df)*a
index=df.isnull().sum()<b
index_dict=dict(index)
columns_list=list(df.columns)
for i in range(len(columns_list)):
    if index_dict[columns_list[i]]==False:
        df=df.drop(columns_list[i],axis=1)

2-3. カテゴリデータの扱い

今回は回帰問題なので、すべての特徴量を数値のみで表現することを目標にしました。
これでもまだ欠損値は残っているので、それらを何らかの値で補完したいのですが、その前にカテゴリデータに対して、ダミー変数化とマッピングを施そうと思います。

• まず、特徴量を型ごとに分類します。
• そして、ダミー変数化・マッピングをするためのリストを作ります。
• マッピングのためにも辞書を作ります。

#変数を型ごとに分ける
df_int=df.select_dtypes(include='int')
df_float=df.select_dtypes(include='float')
df_object=df.select_dtypes(include='object')

#カテゴリー変数を抽出
categorial_feature_names=['MSZoning', 'Street', 'LotShape', 'LandContour', 'Utilities',
       'LotConfig', 'LandSlope', 'Neighborhood', 'Condition1', 'Condition2',
       'BldgType', 'HouseStyle', 'RoofStyle', 'RoofMatl', 'Exterior1st',
       'Exterior2nd', 'MasVnrType', 'ExterQual', 'ExterCond', 'Foundation',
       'BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2',
       'Heating', 'HeatingQC', 'CentralAir', 'Electrical', 'KitchenQual',
       'Functional', 'GarageType', 'GarageFinish', 'GarageQual', 'GarageCond',
       'PavedDrive', 'SaleType', 'SaleCondition']
#その中でmappingする変数を抽出
mapping_feature_names=['Utilities', 'ExterQual', 'ExterCond', 
       'BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2',
        'HeatingQC',  'KitchenQual',
       'Functional', 'GarageFinish', 'GarageQual', 'GarageCond',
       'PavedDrive']
#ダミー変数化
df_before_dummy=df_object.drop(mapping_feature_names,axis=1)
df_dummy=pd.get_dummies(df_before_dummy)
#mapping辞書作成（nanの辞書を入れているのはtestデータ用）
feature_values=[['AllPub','NoSewr','NoSeWa','ELO'],['Ex','Gd','TA','Fa','Po'],['Ex','Gd','TA','Fa','Po'],
                ['Ex','Gd','TA','Fa','Po','NA'],['Ex','Gd','TA','Fa','Po','NA'],['Gd','Av','Mn','No','NA'],['GLQ','ALQ','BLQ','Rec','LwQ','Unf','NA'],
               ['GLQ','ALQ','BLQ','Rec','LwQ','Unf','NA'],['Ex','Gd','TA','Fa','Po'],['Ex','Gd','TA','Fa','Po'],
               ['Typ','Min1','Min2','Mod','Maj1','Maj2','Sev','Sal'],['Fin','RFn','Unf','NA'],
               ['Ex','Gd','TA','Fa','Po','NA'],['Ex','Gd','TA','Fa','Po','NA'],['Y','P','N']]
mapping_list=[]
dic_nan={np.nan:0}
for i in range(len(feature_values)):
    keys=feature_values[i]
    values=reversed(range(1,len(feature_values[i])+1))
    dic=dict(zip(keys,values))
    dic.update(dic_nan)
    mapping_list.append(dic)

    
#mapping実行
df_mapping=df_object.loc[:,mapping_feature_names]
for i in range(len(mapping_feature_names)):
    df_mapping[mapping_feat]

これで無事、すべてのデータが数値型になりました。

##2-4. 欠損値補完
型ごとに欠損値を補完します。

#int型の欠損値を0で補う
df_int=df_int.fillna(0)
#float型も欠損値を平均値で補う
df_float=df_float.fillna(df_float.mean())
#数値型として結合
df_number=pd.concat([df_int,df_float],axis=1).astype(float)

そして新しくデータフレームを作成します。

#説明変数用のデータフレーム
df_x=pd.concat([df_number,df_dummy,df_mapping],axis=1)
#priceも合わせたデータフレーム
df_clean=pd.concat([df_x,df_price],axis=1)

##2-5. shapeの確認
2-1から2-4と同じ作業をtestデータに対しても行います。
ここでそれぞれのデータのshapeを確認します。

print(df_train.shape,df_test.shape)
print(df_x.shape,df_x_val.shape)

(1456, 80) (1459, 79)
(1456, 217) (1459, 204)

• データ数 : 外れ値の削除より1460→1456に減少(trainデータ)
• columns : trainデータとtestデータで異なっている。

columns の数に違いが生じているのは、ダミー変数化が原因です。
これを簡単な例を用いて下に示します。
例）

train=pd.DataFrame({'Alphabet':['A','B','C','C']})
test=pd.DataFrame({'Alphabet':['A','B','D','E']})
train=pd.get_dummies(train)
test=pd.get_dummies(test)

trainデータからは
A B C
1 0 0
0 1 0
0 0 1
0 0 1

が得られ、

testデータからは
A B D E
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

が得られる。

これではcolumnsが異なったままなのでtrainデータから作成したモデルにtestデータを入力するとエラーが出てしまうので、上のような操作を行う必要があるのです。

##2-6. columnsの調整
お互いに足りないcolumnがあるのでそれを補完し、その値はすべて0とします。

#columnsを揃える
missing_columns=set(df_x.columns)-set(df_x_val.columns)
for column in missing_columns:
    df_x_val[column]=0

missing_columns_sub=set(df_x_val.columns)-set(df_x.columns)
for column in missing_columns_sub:
    df_x[column]=0

print(df_train.shape,df_test.shape)
print(df_x.shape,df_x_val.shape)
print(set(df_x.columns)==set(df_x_val.columns))

(1456, 80) (1459, 79)
(1456, 217) (1459, 217)
True

これで説明変数の前処理は終了です。

#3. 'SalePrice'の確認
回帰問題なので、目的変数Yに関してはきちんと調べておくべきです。

基本統計量を表示します。

print(df_price.describe())

count      1456.000000
mean     180151.233516
std       76696.592530
min       34900.000000
25%      129900.000000
50%      163000.000000
75%      214000.000000
max      625000.000000

機械学習のアルゴリズムは変数が正規型に近い方が精度の良いモデルを構築することができます。
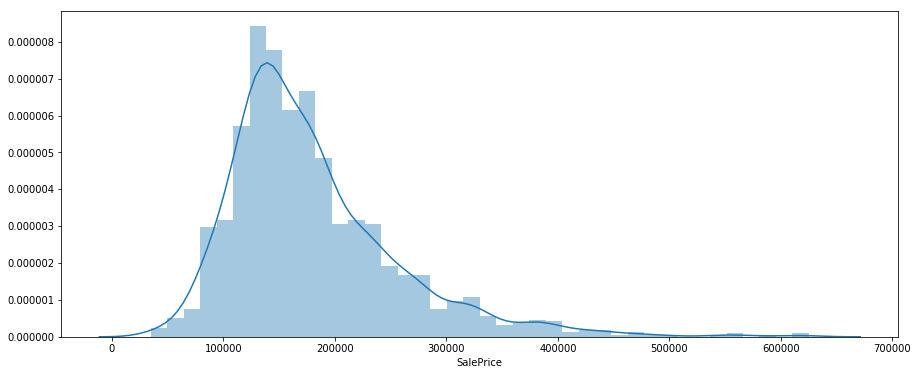
今回は'SalePrice'の分布を出力すると左側に歪みが生じていたので、y=log(x)を用いて正規分布に近い形になるようにしました。よって、目的変数としてlog(SalePrice)を用いることにするので、結果を提出する際にはy=exp(x)を適用することを忘れないようにします。

• SalePriceの分布

plt.figure(figsize=(15,6))
sns.distplot(df_price)

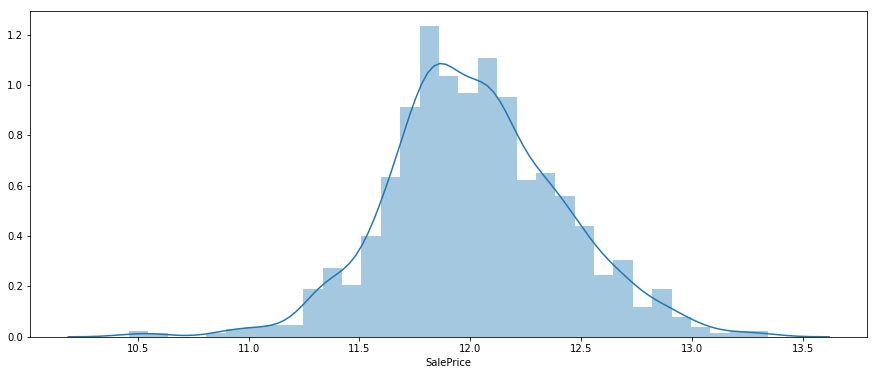
• log(SalePrice)の分布

plt.figure(figsize=(15,6))
sns.distplot(df_log_price)

見ての通り、かなり正規型い近づきました！
これを目的変数として分析をしていきます。

#4. 特徴量の選択

##4-1.相関係数の確認
とりあえず、相関係数の高い20個の特徴量を表示します。

corr_with_price=pd.DataFrame(df_clean.corr().iloc[:,-1])
corr_with_price.columns=['相関係数']
corr_with_price['絶対値']=abs(corr_with_price['相関係数'])
corr_with_price=corr_with_price.drop('SalePrice')
corr_with_price.sort_values('絶対値',ascending=False).head(20)

	              相関係数	  絶対値
OverallQual	      0.800858	0.800858
GrLivArea	      0.720516	0.720516
ExterQual	      0.694628	0.694628
KitchenQual	      0.666217	0.666217
GarageCars	      0.649256	0.649256
TotalBsmtSF	      0.646584	0.646584
GarageArea	      0.636964	0.636964
1stFlrSF	      0.625235	0.625235
FullBath	      0.559048	0.559048
BsmtQual	      0.551670	0.551670
GarageFinish	      0.541968	0.541968
TotRmsAbvGrd	      0.537462	0.537462
YearBuilt	      0.535279	0.535279
YearRemodAdd	      0.521428	0.521428
Foundation_PConc      0.505863	0.505863
GarageYrBlt	      0.481640	0.481640
MasVnrArea	      0.476413	0.476413
Fireplaces	      0.466765	0.466765
HeatingQC	      0.435081	0.435081
Neighborhood_NridgHt  0.419524	0.419524

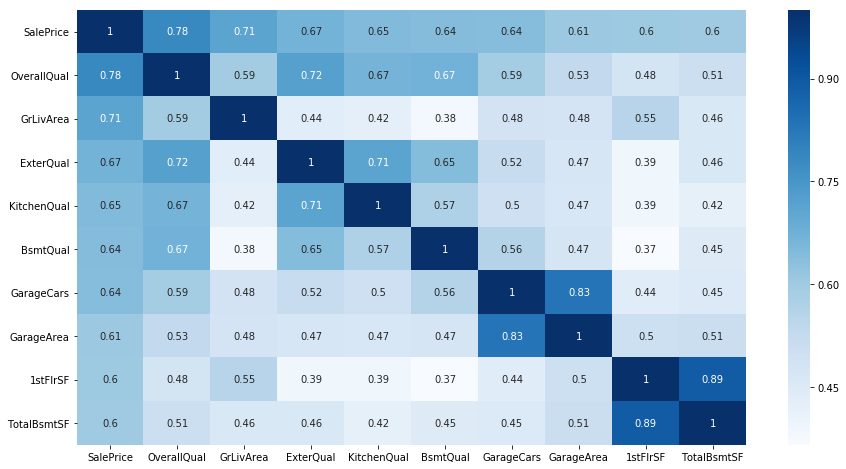
相関の強いtop15に関してheatmapを作成しました。

sns.heatmap(df_pickup.corr(),cmap='Blues',annot=True)

そして、相関係数の高い特徴量についてSalePriceとの関係を可視化します。

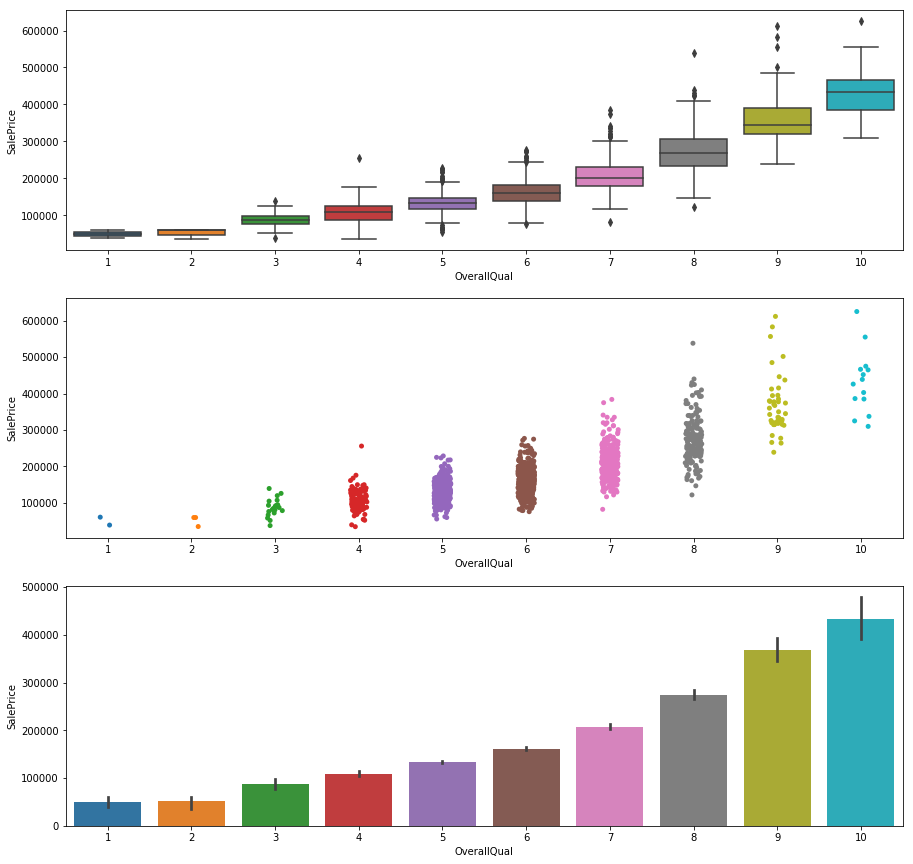
• OverallQual

plt.figure(figsize=(15,15))
plt.subplot(3, 1, 1)
sns.boxplot(x="OverallQual", y="SalePrice", data=df_train)
plt.subplot(3, 1, 2)
sns.stripplot(x="OverallQual", y="SalePrice", data=df_train, size = 5, jitter = True);
plt.subplot(3, 1, 3)
sns.barplot(x="OverallQual", y="SalePrice", data=df_train)

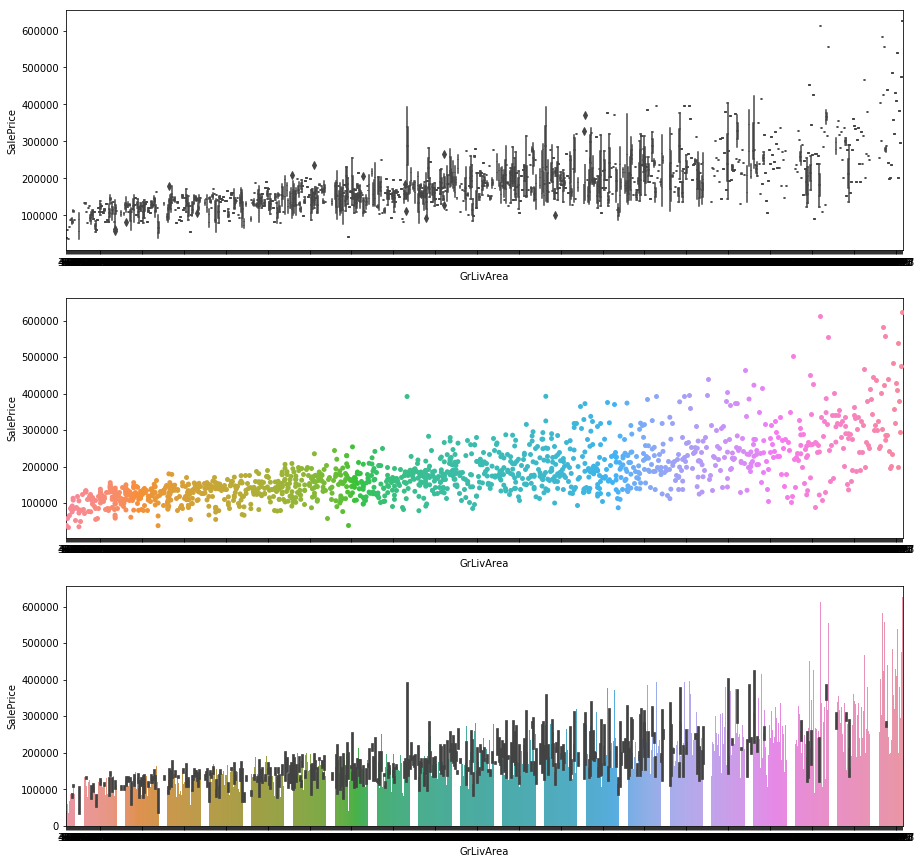
• GrLivArea

plt.figure(figsize=(15,15))
plt.subplot(3, 1, 1)
sns.boxplot(x="GrLivArea", y="SalePrice", data=df_train)
plt.subplot(3, 1, 2)
sns.stripplot(x="GrLivArea", y="SalePrice", data=df_train, size = 5, jitter = True);
plt.subplot(3, 1, 3)
sns.barplot(x="GrLivArea", y="SalePrice", data=df_train)

##4-2. 特徴量選択
今回は、機械学習モデルとして、['GradientBoostingRegressor','RandomForestRegressor','Ridge','ElasticNet','Lasso']を用いるので、特徴量が多くても問題はないので、
priceと相関の高い特徴量を175個取り出して、説明変数とします。

#変数を減らす
#相関の絶対値top175
pickup_features=corr_with_price.sort_values('絶対値',ascending=False).head(175).index
df_pickup=df_x[pickup_features]
df_pickup_val=df_x_val[pickup_features]

##4-3. 標準化してデータ準備

#データ準備
#説明変数は標準化
#目的変数はlogを取って正規分布に近い形にする
ss=StandardScaler()
x=df_pickup.values
x_std=ss.fit_transform(x)
y=df_price.apply(np.log).values
x_train,x_test,y_train,y_test=train_test_split(x_std,y,random_state=2,test_size=0.3)
#testdataも
ss_val=StandardScaler()
x_val=ss_val.fit_transform(df_pickup_val.values)

そしてこれから、モデルを構築し、パラメータ調整をしていきます。

#5. 機械学習モデル構築
今回は['GradientBoostingRegressor','RandomForestRegressor','Ridge','ElasticNet','Lasso']を用います。
パラメータ調整はグリッドサーチ法で探索します。
結果を下に記します。
今回のコンペはRMSEで評価されるのでこれも合わせて出力します。

##5-1. GradientBoostingRegressor

#gradientboostingregrsoor
params_grad={'n_estimators':[50,60],'max_depth':[3,4,5],'learning_rate':[0.1,0.05,0.2]}
kf=KFold(n_splits=10,random_state=0,shuffle=True)
gs_grad=GridSearchCV(GradientBoostingRegressor(),params_grad,cv=kf)
gs_grad.fit(x_train,y_train)
print(gs_grad.score(x_train,y_train))
print(gs_grad.score(x_test,y_test))
print(gs_grad.best_params_)
print(rmse(gs_grad,x_test,y_test))

0.9697823386182204
0.9033132054244156
{'learning_rate': 0.2, 'max_depth': 3, 'n_estimators': 60}
0.12233638041421158

確認のため、残差プロットもしておきます。

def res_plot(y_train,y_train_pred,y_test,y_test_pred):
    y_train_res=y_train-y_train_pred
    y_test_res=y_test-y_test_pred
    
    plt.figure(figsize=(8,8))
    plt.scatter(y_train_pred,y_train_res,color='blue',marker='o',label='train')
    plt.scatter(y_test_pred,y_test_res,color='green',marker='o',label='test')
    plt.xlabel('y_pred')
    plt.ylabel('y_res')
    plt.legend()
    plt.hlines(y=0,color='red',xmin=10,xmax=14)
        
res_plot(y_train,gs_grad.predict(x_train),y_test,gs_grad.predict(x_test))

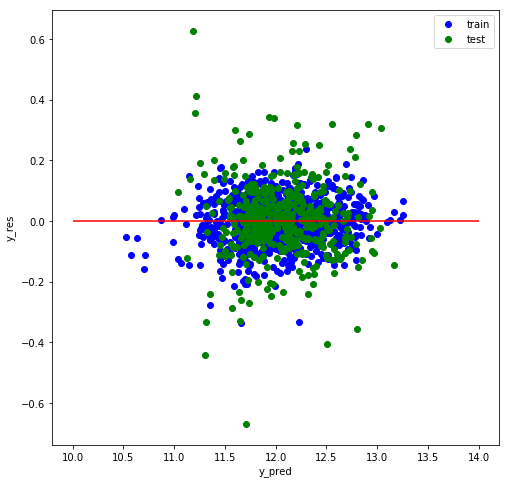
これから、残差は正規型に近く、線型性も見られないのでとりあえずオッケーにしました。

##5-2. Ridge回帰

#ridge回帰
params_ridge={'alpha':[100,150,200]}

gs_ridge=GridSearchCV(Ridge(),params_ridge,cv=kf)
gs_ridge.fit(x_train,y_train)
print(gs_ridge.score(x_train,y_train))
print(gs_ridge.score(x_test,y_test))
print(gs_ridge.best_params_)
print(rmse(gs_ridge,x_test,y_test))

0.9381824820312565
0.9249581813596081
{'alpha': 150}
0.10777641189162118

##5-3. ElasticNet

#ElasticNet
params_net={'alpha':[0.055,0.01,0.05,0.08],'l1_ratio':[0.1,0.06,0.05]}
gs_net=GridSearchCV(ElasticNet(),params_net,cv=kf)
gs_net.fit(x_train,y_train)
print(gs_net.score(x_train,y_train))
print(gs_net.score(x_test,y_test))
print(gs_net.best_params_)
print(rmse(gs_net,x_test,y_test))

0.9353791278282626
0.9273181800859842
{'alpha': 0.05, 'l1_ratio': 0.06}
0.10606813732517212

##5-4. Lasso回帰

#Lasso回帰
params_lasso={'alpha':[0.01,0.005,0.001,0.1]}
gs_lasso=GridSearchCV(Lasso(),params_lasso,cv=kf)
gs_lasso.fit(x_train,y_train)
print(gs_lasso.score(x_train,y_train))
print(gs_lasso.score(x_test,y_test))
print(gs_lasso.best_params_)
print(rmse(gs_lasso,x_test,y_test))

0.9320411350154312
0.9272945479607099
{'alpha': 0.005}
0.10608537968228171

#6. アンサンブル学習
後は、これら4つのモデルにvalididationデータを入力し、その結果の平均をとって'SalePrice'とし、kaggleに提出しました。
train.csvからのデータではsplitしたtrainデータ,testデータともに精度92%でRMSEのスコアも0.11ほどでしたが、提出したtest.csvからのRMSEスコアは0.124と少し低くなってしまいました。過学習が起こっていた可能性がありますね。

#結果まとめ

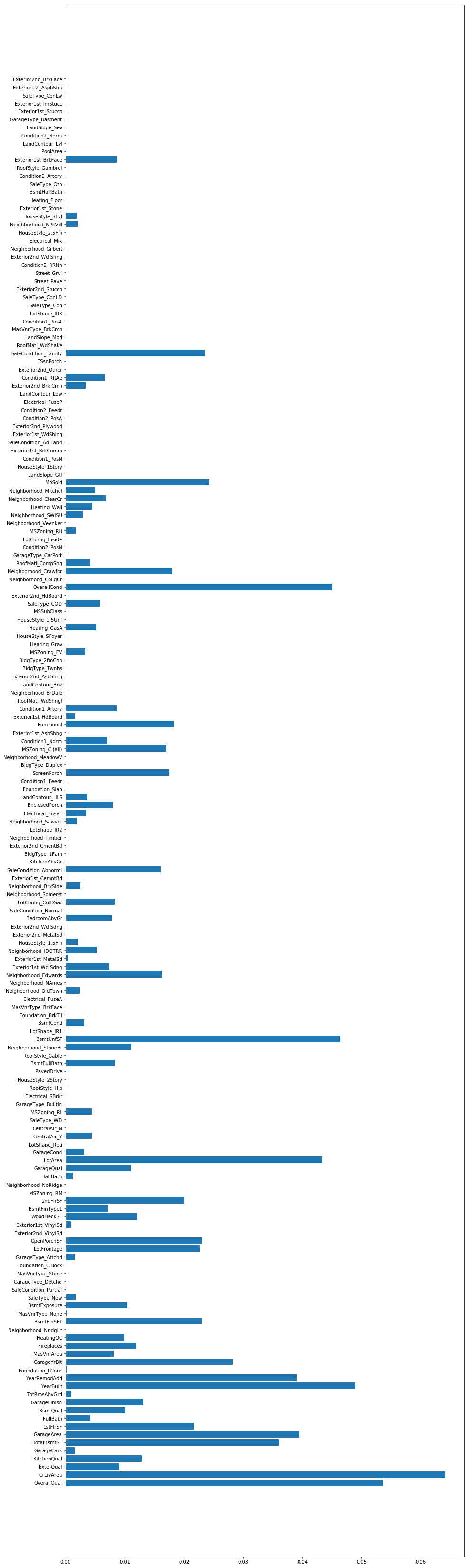
先ほどパラメータ調整したGradeintBoostingRegressorで重要な特徴量を可視化してみます。

#重要な特徴量

gs_grad2=GradientBoostingRegressor(n_estimators=60,learning_rate=0.2,max_depth=3)
gs_grad2.fit(x_train,y_train)
important=gs_grad2.feature_importances_
n_features=len(important)
plt.figure(figsize=(15,60))
plt.barh(range(n_features),important,align='center')
plt.yticks(np.arange(n_features),df_pickup.columns)
plt.show()

これを見ると、'GrLivArea'、'OverallQual'、'Yearbuilt'の特徴量がtop3に入ってくることがわかります。
よって、購買者はまずこれらの条件を元に家の購入を考えている可能性が高いです。特に'OverallQual'というのは、客観的な数値では無く、不動産会社が査定した上で決めている数値なので、この値の決定に関しては少し慎重に決めるべきではないでしょうか。
他の数値の高い特徴量を見ても'SF'や'Qual'といったものが目立ちます。やはり、家の面積や質そのものといったものに大きな価値を見出していることもわかります。

#振り返り

• 特徴量として、priceと相関の強いものを175個選んだわけだが、これを50,100,150,200などと変化させた上で最も精度がよかったのが今回の記事です。やはり、モデル云々の前に前処理、並びに特徴量選択が重要だなと感じました。
• 4つのモデルの中で最も精度のよかったElasticNetを採用するより、平均をとって提出した方がスコアはよかったです。
• stackingという手法を用いて最終結果を出力する方法も試したましたが、スコアは平均とった時の方がよかったです。

（参考：stacking）

#stackingのためのデータフレーム作成

predict_grad=gs_grad.predict(x_test)
predict_net=gs_net.predict(x_test)
predict_lasso=gs_lasso.predict(x_test)

df_final=pd.concat([pd.DataFrame(predict_grad),pd.DataFrame(predict_ridge),
                    pd.DataFrame(predict_net),pd.DataFrame(predict_lasso),
                    pd.DataFrame(y_test)],
                   axis=1)
df_final.columns=['GradientBoostingRegressor','Ridge','ElasticNet','Lasso','y_test']
#stackingのモデル生成
#Lasso回帰を用いるのでlassoの結果は外す
x_final=df_final.drop('y_test',axis=1).drop('Lasso',axis=1).values
y_final=df_final['y_test'].values

ss_final=StandardScaler()
x_std_final=ss_final.fit_transform(x_final)

reg_params={'alpha':[0.1,0.01,0.005,0.002]}
reg=GridSearchCV(Lasso(),reg_params,cv=kf)
reg.fit(x_std_final,y_final)
print(reg.best_params_)
print(reg.score(x_std_final,y_final))
print(rmse(reg,x_std_final,y_final))

{'alpha': 0.005}
0.9299047050915786
0.10416371946180343

#次に向けて
##①前処理

• 地域ごとに分類して欠損補完して見る
• quality,area,regionなどと言った新しい特徴量を作成する
• 特徴量の2乗、3乗や指数関数と言った変数を作成する（例えばSalePriceとOverallQualには指数関数的な関係が見られた）

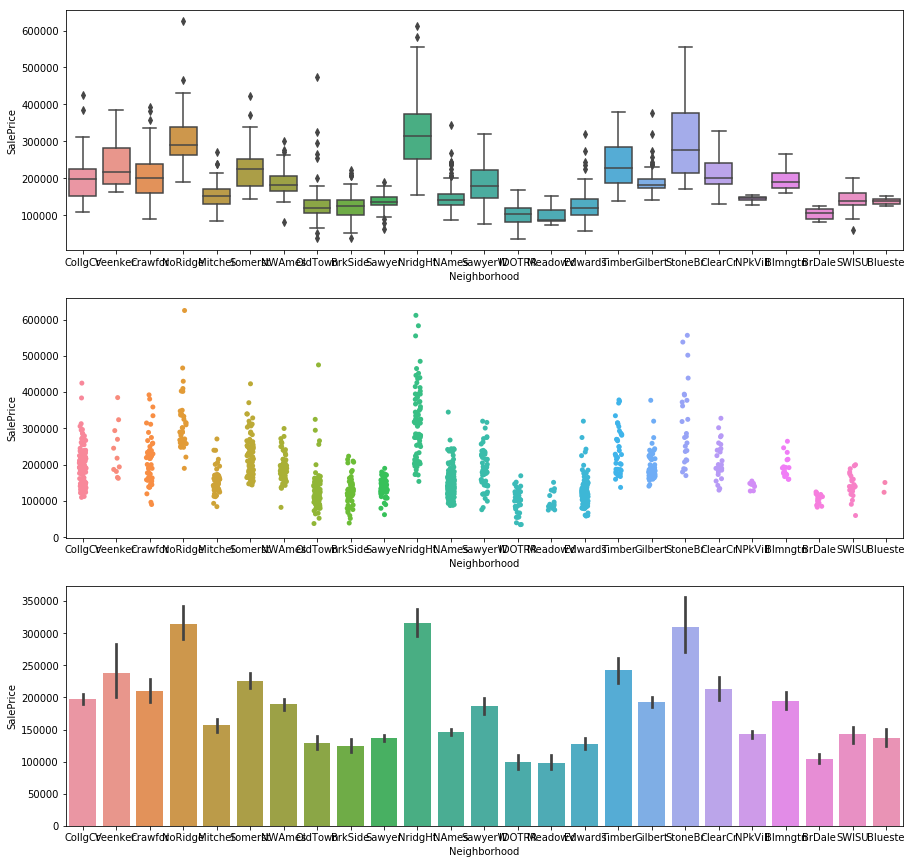
plt.figure(figsize=(15,15))
plt.subplot(3, 1, 1)
sns.boxplot(x="Neighborhood", y="SalePrice", data=df_train)
plt.subplot(3, 1, 2)
sns.stripplot(x="Neighborhood", y="SalePrice", data=df_train, size = 5, jitter = True);
plt.subplot(3, 1, 3)
sns.barplot(x="Neighborhood", y="SalePrice", data=df_train)

##②特徴量選択

• RGboostを用いた特徴量選択をやってみる（今回はメモリ不足でエラー発生、そして時間が無く勉強できなかった）
• 今回は相関係数の高いものを選んだが、相関が高いからと言って重要な特徴量だということではない、ということに注意したい

##③アルゴリズム選択

• もっと多くの機械学習モデルを作ってアンサンブル学習をさせる
• 先に述べたようにstackingという手法をマスターして使えるようにする

これらのことを意識してこれからもデータ分析をしていこうと思います。今後ともよろしくお願い致します。