主成分分析とEigenface

はじめに

前回の投稿では参考書籍を元に特異値分解の基礎についてを備忘を記した。
今回はその特異値分解と主成分分析の関係、およびYale databaseを用いた実演を行う。

概要

前記事の通り、主成分分析(Principal Component Analysis；PCA)は特異値分解の応用のひとつである。
その恩恵というは、高次元データを表すための階層座標系の解釈を統計的に与えてくれることだ。
このあたりの概要は20世紀初頭から擦られまくっているのでこれ以上は言及しない。

計算方法

まずは標本平均を$0$にする処理を行う。
データセット$\boldsymbol{X}$の列平均$\bar{\boldsymbol{x}_j}$は次のように与えられる。

\bar{\boldsymbol{x}_j}=\frac{1}{n}\sum_{i=1}^n\boldsymbol{X}_{ij} \tag{1}\label{a}

そして、平均行列$\bar{\boldsymbol{X}}$は

\bar{\boldsymbol{X}}=
\begin{bmatrix}
1 \\
\vdots \\
1 \\
\end{bmatrix}\bar{\boldsymbol{x}}\tag{2}\label{b}

となる。
ここで行列$\boldsymbol{B}$を行列$\boldsymbol{X}$から$\bar{\boldsymbol{X}}$を引いたものとして、共分散行列$\boldsymbol{C}$は以下の式で表せられる。

\begin{align}
\boldsymbol{B}&=\boldsymbol{X}-\bar{\boldsymbol{X}}\tag{3}\label{c}\\
\Rightarrow \boldsymbol{C}&=\frac{1}{n-1}\boldsymbol{B}^*\boldsymbol{B}\tag{4}\label{d}
\end{align}

右辺の係数部分の分子が$n$ではなく$n-1$としているのは、Bessel補正と呼ばれる母集団の統計量推定を図ったものである。
主成分とはまさにこの共分散行列$\boldsymbol{C}$の固有ベクトルなのだが、これは$\boldsymbol{C}$が対角行列となる座標変化を表現する。

\boldsymbol{C}\boldsymbol{D}=\boldsymbol{V}\boldsymbol{D}
\Rightarrow\boldsymbol{C}=\boldsymbol{V}\boldsymbol{D}\boldsymbol{V}^*
\Rightarrow\boldsymbol{D}=\boldsymbol{V}^*\boldsymbol{C}\boldsymbol{V}\tag{5}\label{e}

固有行列$\boldsymbol{V}$の列ベクトルが主成分であり、対角行列$\boldsymbol{D}$の要素が各固有ベクトルの方向に沿ったデータの分散を表す。$\boldsymbol{C}$はエルミートであり、$\boldsymbol{V}$の列ベクトルは互いに直交することから、上式の等式は常に存在することが保証される。

さて、固有行列$\boldsymbol{V}$は$\boldsymbol{B}$の右特異ベクトルでもあるので、(この証明は下記プルダウンをクリック)

証明

\begin{align}
\boldsymbol{X}^*\boldsymbol{X}&=\boldsymbol{V}
\begin{bmatrix}
\hat{\boldsymbol{\Sigma}} & \boldsymbol{0}
\end{bmatrix}
\boldsymbol{U}^*
\boldsymbol{U}
\begin{bmatrix}
\hat{\boldsymbol{\Sigma}} \\
\boldsymbol{0}
\end{bmatrix}
\boldsymbol{V}^*\\
\Rightarrow\boldsymbol{X}^*\boldsymbol{X}\boldsymbol{V}&=\boldsymbol{V}\hat{\boldsymbol{\Sigma}}^2
\end{align}

\begin{align}
\boldsymbol{C}&=\frac{1}{n-1}\boldsymbol{B}^* \boldsymbol{B} \tag{6}\label{f}\\
&=\frac{1}{n-1}\boldsymbol{V}\boldsymbol{\Sigma}^2 \boldsymbol{V}^*\tag{7}\label{g}\\
\Rightarrow \boldsymbol{D}&=\frac{1}{n-1}\boldsymbol{\Sigma}^2\tag{8}\label{h}
\end{align}

これらの座標における分散は$\boldsymbol{D}$の対角要素$\lambda_k$で与えられ、次のように特異値に関係する。

\lambda_k =\frac{\sigma_k^2}{n-1}\tag{8}\label{i}

このようにSVDはPCAを計算するに際して数値計算的に頑健な手段となっている。

Eigenfacesデータセットによる固有顔の計算

本章ではExtended Yale Face Database Bを用いたデモを行う。
このデータセットは38人のトリミング済顔写真が9つの姿勢と64パターンの光量から構成されたものである。また、画像は192×168=32,256pixelと縦長になっており、生データでは列ベクトルに平板化されて格納されている。

では、実際にデータを読み込んで先頭36人の顔を表示してみよう。

### import libraries
from matplotlib.image import imread
import matplotlib.pyplot as plt
import numpy as np
import scipy

### read data
contents = scipy.io.loadmat('../data/allFaces.mat')
faces = contents['faces']
nfaces = np.ndarray.flatten(contents['nfaces'])
m = int(contents['m'][0,0])
n = int(contents['n'][0,0])

### display several faces
persons = np.zeros((6*n, 6*m))
count = 0
for i in range(6):
    for j in range(6):
        persons[i*n:(i+1)*n, j*m:(j+1)*m] = np.reshape(faces[:, np.sum(nfaces[:count])], (m, n)).T
        count += 1
image = plt.imshow(persons)

ここまで実行すると、下記のような画像が表示される。
[出力結果]

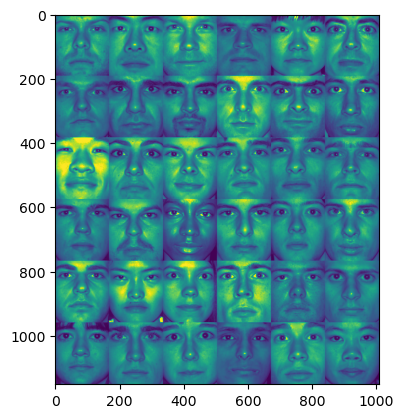
因みに変数nfacesは同一人物で異なる光量、姿勢のデータ数を表している。
実際に、出力してみると

print(nfaces)
fig, (ax1, ax2, ax3) = plt.subplots(1, 3)
pattern_1 = ax1.imshow(np.reshape(faces[:,0], (m, n)).T)
pattern_2 = ax2.imshow(np.reshape(faces[:,63], (m, n)).T)
pattern_3 = ax3.imshow(np.reshape(faces[:,64], (m, n)).T)
plt.show()

[出力結果]
[64 62 64 64 62 64 64 64 64 64 60 59 60 63 62 63 63 64 64 64 64 64 64 64 64 64 64 64 64 64 64 64 64 64 64 64 64 64]

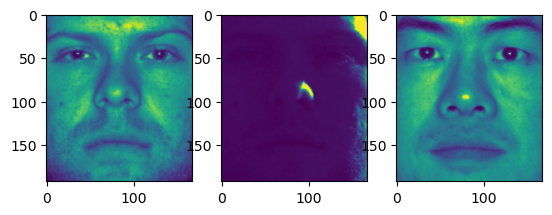
一人目の人物は添字で言う0~63までであり、64からは二人目となっていることが分かった。
次に、この36人の平均顔を計算してみる。式$\ref{b}$を元に

### Using the first 36 people for training data
training_faces = faces[:, :np.sum(nfaces[:36])]
average_face = np.mean(training_faces, axis=1)
plt.imshow(np.reshape(average_face, (m, n)).T)

[出力結果]

余談であるが、人間を含む哺乳類(というか有性生殖を行う動物全て)は突然変異が起こらないので、つがいを成しお互いの遺伝子を交換することで生物としての多様性を生み出すことで環境変化に対応できる生存戦略を取っている。平均顔が美男美女になる、と耳にしたことがあるかも知れないが、これは当たり障りない(=平均化された)顔が本能的に環境変化に対応しやすい遺伝子だと認識されているため、という一説があるらしい。

さて、ここで漸く本題である固有顔の計算に入る。
式$\ref{c}$を参考として、行列$\boldsymbol{X}\in\mathbb{C}^{32,356\times 2,282}$として標本平均を0に変換し、SVDを適用する。($c.f.\text{式}\ref{c}$)
例として左特異行列の1列目を抽出して表示してみる。

### Compute eigenfaces on mean-subtracted training data
X = training_faces-np.tile(average_face, (training_faces.shape[1], 1)).T
U, S, Vh = np.linalg.svd(X, full_matrices=False)
plt.imshow(np.reshape(U[:, 0], (m, n)).T)

このデータセットにはのべ38人の個人の顔が使用されているが、37,38番目の人間を固有顔計算に入れずに検証用として置いてあるのであった。
では、この36人の顔で作られた固有空間で37人目、38人目が再現できるのか試してみる。
左特異行列$\boldsymbol{U}$を階数$r$で切ったものを$\tilde{\boldsymbol{U}}$として

\tilde{\boldsymbol{x}}_\text{test}=\tilde{\boldsymbol{U}}\tilde{\boldsymbol{U}}^*\boldsymbol{x}_\text{test}

### Approximate test image omitted from training data
def display(ax, idx, img, title):
    ax[idx[0], idx[1]].imshow(np.reshape(img, (m, n)).T)
    ax[idx[0], idx[1]].set_title(title)
    ax[idx[0], idx[1]].get_xaxis().set_visible(False)
    ax[idx[0], idx[1]].get_yaxis().set_visible(False)
    return ax

test_face = faces[:,np.sum(nfaces[:36])]
Xt = test_face-average_face
r_list = [25, 50, 100, 200, 400, 800, 1600]
fig, ax = plt.subplots(2, 4, tight_layout=True)
ax = display(ax, (0, 0), test_face, 'original')
for i, r in enumerate(r_list):
    recon_face = average_face+U[:,:r]@U[:,:r].T@Xt
    ax = display(ax, ((i+1)//4, (i+1)%4), recon_face, f'r={r}')
plt.show()

[出力結果]

興味深いことにこの固有空間は人間の顔以外も表現することができる。
実際に前回の投稿で用いた画像をテストデータに、上と同様の処理をするとこのような結果となる。

まとめ

前回記事では、特異値分解を用いて信号圧縮についてまとめた。画像を圧縮する方法には2つあり、1つ目は画像そのもののSVDを取って、主成分である$\boldsymbol{U}$と$\boldsymbol{V}$の列を保持する方法、2つ目は本記事で述べた、画像を固有画像の線形結合として表現する方法である。前者の方法はあまり効率的でないが、後者は一度計算して保存した特定の基底$\boldsymbol{U}$を使用することで、人間の顔などの特定のクラスの画像を圧縮できる。この特定の基底は、学習に役立つ相関特徴として解釈できるという追加の利点もある。