ぶぅちゃんズ Advent Calendar 2019担当2日目。
今回は、AutoEncoderをPCAの負荷量ベクトルでパラメータ初期化してファインチューニングする。ただそれだけ。
AutoEncoder(自己符号化器)
情報工学を専攻している人間なら一度は聞いたことがあるだろう。まして機械学習を専攻してる人間は必ずといって講義や研究、論文に出てくると思う。ここでは筆者の確認程度に解説を行う。
AutoEncoderは対称のニューラルネットアーキテクチャに入力データと出力データに同じデータを学習させるものである。
例として、入力・出力ユニット数=5、中間ユニット数=3のAutoEncoderを考えてみる。

画像左側から5次元のデータが入力され、一度3次元になったのち、元のデータが出力されるように学習が行われる。すなわち、学習済みのニューラルネットワーク左半分(下画像で実線部分、Encoderと呼ばれる。)だけを取り出すと、データの次元圧縮が行われていることがわかる。(図テキトーでごめんなさい。)

ここで、入力データを$\boldsymbol{x}\in\boldsymbol{R}^d$、出力データを$\boldsymbol{l}\in\boldsymbol{R}^d$、Encoderのパラメータ(重み行列)を$\boldsymbol{W}_{enc}\in\boldsymbol{R}^{h\times d}$、Decoderのそれを$\boldsymbol{W}_{dec}\in\boldsymbol{R}^{d\times h}$、活性化関数$\boldsymbol{\sigma}$、損失関数を二乗誤差、学習アルゴリズムは誤差逆伝播法とする。ただし、$0<h<d$。すると、単層AutoEncoderの順伝播は以下の通り。
\boldsymbol{l}=\boldsymbol{\sigma}(\boldsymbol{W}_{dec}\boldsymbol{\sigma}(\boldsymbol{W}_{enc}\boldsymbol{x}))
二乗誤差$J$は
J=\frac{1}{2}\|\boldsymbol{l}-\boldsymbol{x}\|^2
ここで、活性化関数$\boldsymbol{\sigma}$が恒等写像とすれば
\begin{align}
J&=\frac{1}{2}\|(\boldsymbol{W}_{dec}\boldsymbol{W}_{enc}-\boldsymbol{E})\boldsymbol{x}\|^2\\
&=\frac{1}{2}\|\boldsymbol{W}_{dec}\boldsymbol{W}_{enc}-\boldsymbol{E}\|^2\boldsymbol{x}^\mathsf{T}\boldsymbol{x}\\
\Rightarrow\ &\boldsymbol{W}_{dec}\boldsymbol{W}_{enc}-\boldsymbol{E}\rightarrow 0\ i.e.\ J\rightarrow 0
\end{align}
すなわち、行列積$\boldsymbol{W}_{dec}\boldsymbol{W}_{enc}$が単位行列$E\in\boldsymbol{R}^{d\times d}$に近づけば、誤差の少ない次元圧縮ができる。
PCA(主成分分析)
PCAも単層AutoEncoder同様にデータの線形次元圧縮を行う手法である。どう違うか、と聞かれると解答に困る。異なる点は教師なし学習-半教師あり学習くらしか思いつかない。(?)
とりあえずアルゴリズムの概要は以下の通り。
標準化
書いてあるまま。データの各列要素の標本平均を0に標準化する。
負荷量ベクトルの計算
負荷量ベクトルとは分かりやすく言うと、データ$\boldsymbol{x}_i\in\boldsymbol{R}^d$を$N$個並べたデータ行列$\boldsymbol{X}\in\boldsymbol{R}^{N\times d}$に負荷量ベクトル$\boldsymbol{W}\in\boldsymbol{R}^{d\times h}$を掛けて次元圧縮されたデータ$\boldsymbol{t}_i\in\boldsymbol{R}^h$のデータ行列$\boldsymbol{T}\in\boldsymbol{R}^{N\times h}$を得るときの行列$\boldsymbol{W}$である。(説明下手でゴメン。)
このとき、$\boldsymbol{W}=(\boldsymbol{w}_1,\ \boldsymbol{w}_2,...,\boldsymbol{w}_h),\ \boldsymbol{w}_i\in\boldsymbol{R}^d$とすれば、負荷量ベクトルは$\boldsymbol{w}_1$(第一負荷量ベクトル)から順に求める。これはデータの各列の要素のうち、最も分散が大きいものを抽出すれば良い。即ち、固有値を最大化する固有ベクトルを求めれば良いので
\begin{align}
&\begin{cases}
\Lambda=\max_\lambda \{\lambda\mid\boldsymbol{Xw}=\lambda\boldsymbol{w}\}\\\\
\boldsymbol{Xw}_1=\Lambda\boldsymbol{w}_1
\end{cases}
\\
\Rightarrow&\boldsymbol{w}_1=\max_\boldsymbol{w}\{\boldsymbol{w}\neq\boldsymbol{0}\mid\cfrac{\|\boldsymbol{Xw}\|^2}{\|\boldsymbol{w}\|^2}\}
\end{align}
第$k$負荷量ベクトルは第$k-1$番目までの要素を元のデータ行列$\boldsymbol{X}$から除去し、上と同様の操作を行うことで得られる。
とは書くものの、行列$\boldsymbol{X}^\mathsf{T}\boldsymbol{X}$の固有値が大きい順に固有ベクトルを圧縮次元数だけ求めて並べれば負荷量ベクトル$\boldsymbol{W}$が得られる。操作だけなら中学生でも出来る。
ところで、AutoEncoderは$\boldsymbol{W}_{enc}\boldsymbol{x}$で次元圧縮し、PCAは$\boldsymbol{Wx}$でデータの次元圧縮を行う。結論から言うと、この$\boldsymbol{W}_{enc}$とPCAの負荷量ベクトル$\boldsymbol{W}$は理論的には等しくなる。それでは、AutoEncoderのパラメータ初期値をPCAで求めた負荷量ベクトルにすると精度がよくなるのか?(良くなるらしい)というのが本稿の本題である。
すなわち、Encoderに関しては$\boldsymbol{W}_{enc}\leftarrow\boldsymbol{W}$、Decoderは前述より$\boldsymbol{W}_{dec}\boldsymbol{W}_{enc}-\boldsymbol{E}\rightarrow 0$であるから$\boldsymbol{W}_{end}\rightarrow \boldsymbol{W}_{enc}^+$に収束するものとして、$\boldsymbol{W}_{dec}\leftarrow\boldsymbol{W}^+$と初期値設定する。
ただし、行列$\boldsymbol{A}$に関して$\boldsymbol{A}^+$は擬似逆行列を表す。
実験
PCAで求めた負荷量ベクトルをAutoEncoderの初期パラメータに設定し、finetuningして誤差の推移と二次元プロット図を観察する。
データセットはMNIST、フレームワークは今は遺産となったChainerを用いる。
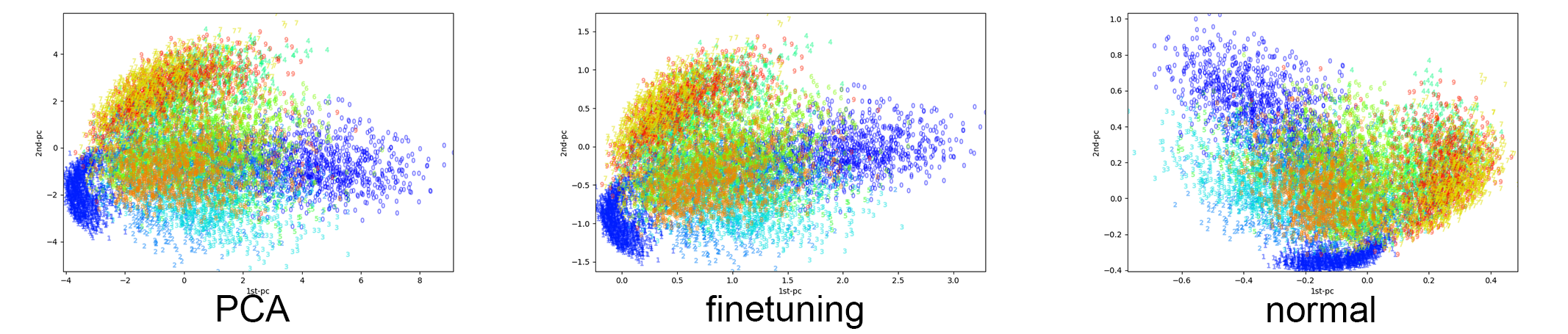
PCA、負荷量ベクトルでパラ初期化したAutoEncoder(finetuning)、初期値ランダムのAutoEncode(normal)それぞれのモデルで$28\times 28$次元のデータを$2$次元まで落とし込み、平面座標にプロットした。AutoEncoderはバッチサイズ=16、エポック数=10で行った。
この図をみると、PCAとfintuningしたAutoEncoderのプロット図は分布が似ているが、初期値がランダムのnormalのAutoEncoderによる次元圧縮プロット図はこの二つとかなり異なった結果になっていることがわかる。
さらに、$28\times 28\rightarrow 16\times16\rightarrow 2$と次元圧縮した2層DeepAutoEncoder(dae)を実装し、初期値ランダムで一層ずつ積層学習を行い最後にfinetuningで学習を行った。それによる平面プロット図は以下の通り。
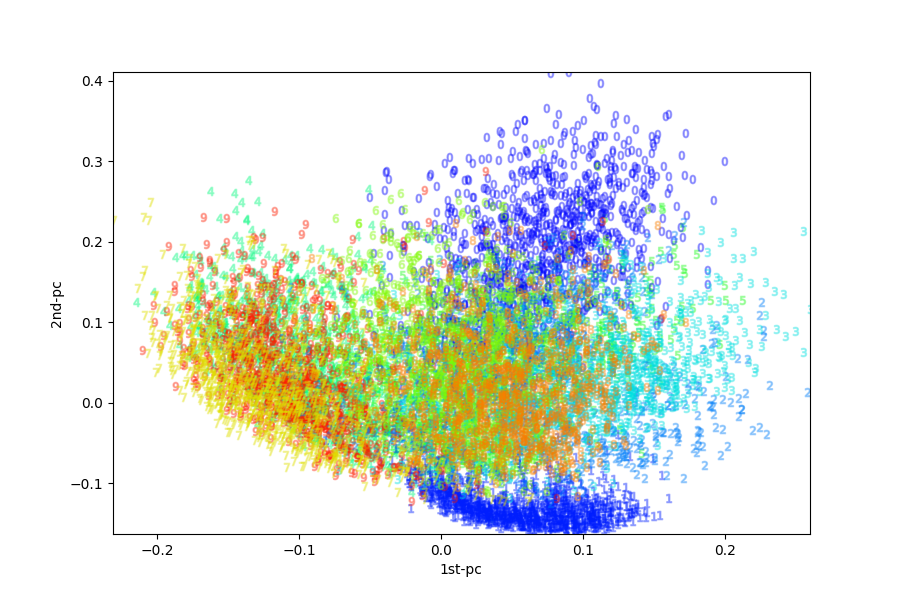
これもまたPCAやfinetuningした単層AutoEncoder、初期値ランダムの単層AutoEncoderとは異なるプロット結果となっている。当然ではあるが、初期値によって次元圧縮の射影結果が異なってくることが見て取れる。
では、次に損失グラフを見てみよう。(※それぞれ一回しか実行していません。)
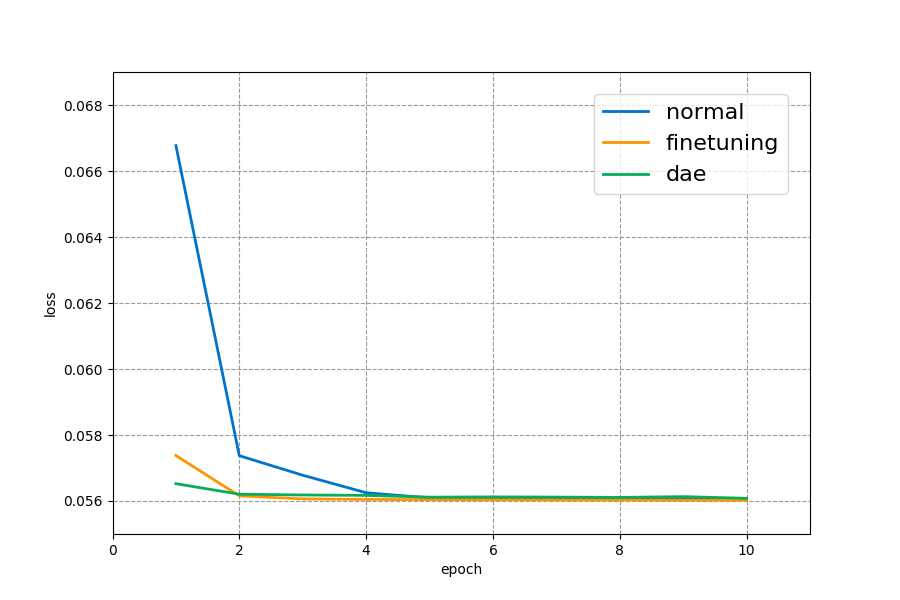
初期値ランダムの単層AutoEncoder(normal)に比較して、負荷量ベクトルで初期化したAutoEncoder(finetuning)やDeepAutoEncoder(dae)は収束速度が早いことが解る。しかしながら、負荷量ベクトルで初期化しているだけあって(finetuning)の方が(dae)より良い収束値を示している。
さて、ここまで来ると最後にはDeepAutoEncoderをPCAで初期化てきないのか?ということを考える。勿論、可能である。
始めに、$28×28\rightarrow 16\times 16$のPCAを実行してその負荷量ベクトルで第一層$\boldsymbol{W}_{enc1}$を初期化し、次に$16\times16\rightarrow 2$のPCAを実行し第二層$\boldsymbol{W}_{enc2}$を初期化する。第三層$\boldsymbol{W}_{dec1}\leftarrow\boldsymbol{W}_{enc2}^+$、第四層$\boldsymbol{W}_{dec2}\leftarrow\boldsymbol{W}_{enc1}^+$とすれば良い。平面プロット図と損失グラフは以下のとおり。
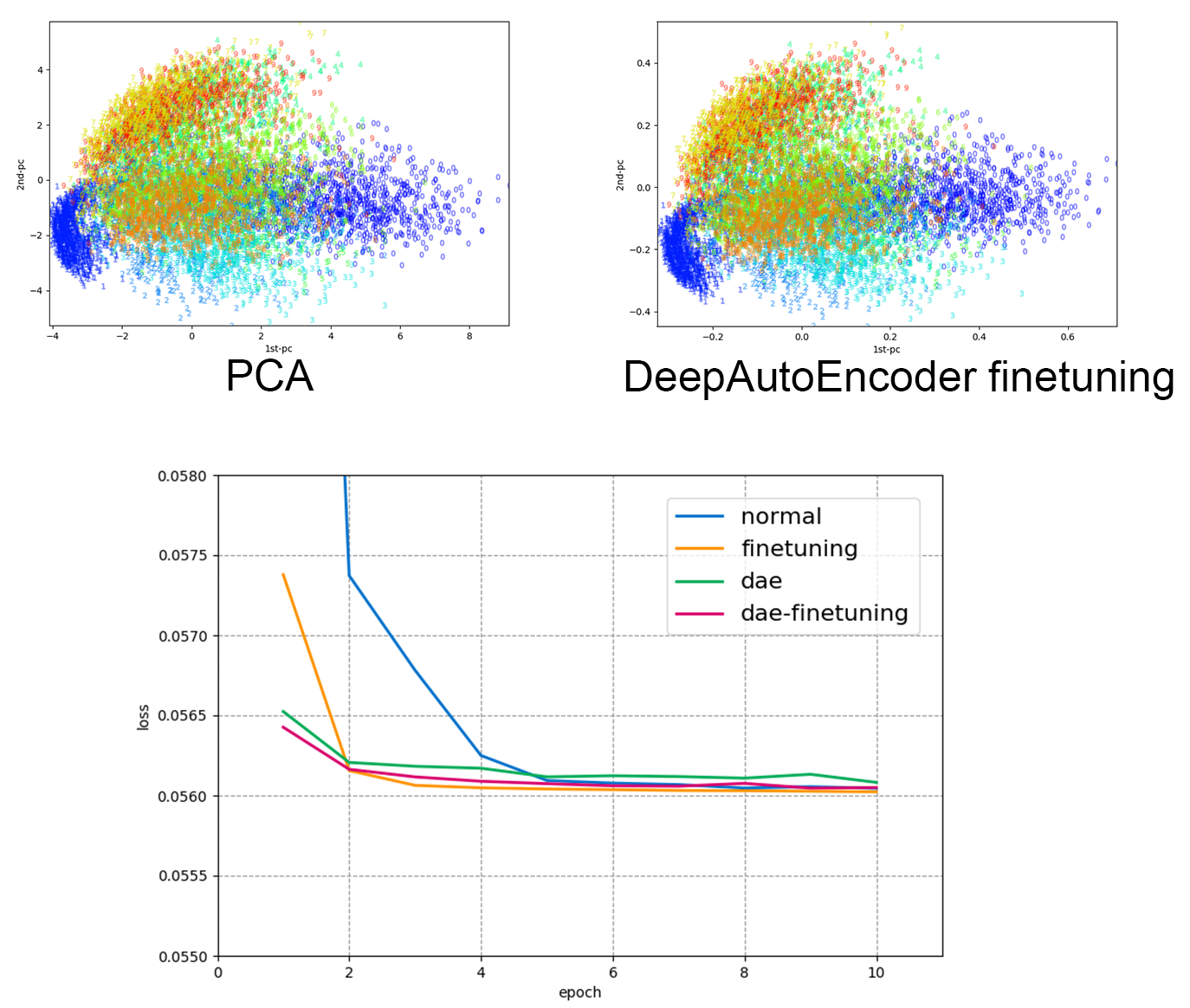
あ、あれ...?
単層AutoEncoderのfintuningの方が精度いいぞ...?(※1回しか実行していません。)
感想
かなりアライさんな検証だけど研究じゃないからいいの。