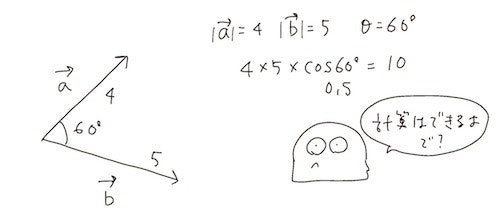プロローグ
ん?どういうこと?ベクトルの内積ナニソレ?
ベクトルの内積?
ベクトルとは?
「え、ぼへちゃんベクトルはわかるよね?」
「矢印みたいなんでしょ」
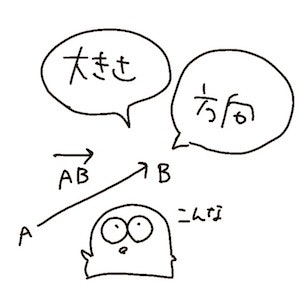
「・・・・・・・ベクトルとは、大きさと向きを兼ね備えた量を表すんだよ。」
「??????うん?」
「一個の数字だけで表現できるものだけじゃないよね。複数の数字でないと表現できないものはたくさんあるよね。」
「例えば、気象の予報とか(気温と気圧)、風の向きとか(風速と風向)、海流の流れとか(温度と速度)。
そういうのを一種のベトルデータとして考えてみることができるんだよ。」
「ほー」
「ここでは、複数の数字のセットで表されるものと考えてみようか」
ベクトルの内積といえば
高校の教科書に出ていたであろう公式です。
\vec{a}・\vec{b} = |\vec{a}||\vec{b}| cosθ \\
思い出しました?
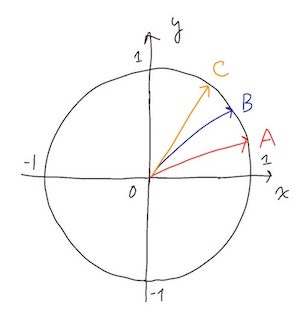
例えば、以下の図のような場合、内積を求めなさいと言う問題の答えを出すには、上記の公式を当てはめて、答えを導き出すことができます。
ここで、ベクトルを成分表示します。ベクトル$\vec{a}$と$\vec{b}$がそれぞれn次元のベクトルだとしたら、以下のようになります
\vec{a} =
\left(
\begin{matrix}
a_{1} \\
a_{2} \\
a_{3} \\
\vdots \\
a_{n} \\
\end{matrix}
\right)
\vec{b} =
\left(
\begin{matrix}
b_{1} \\
b_{2} \\
b_{3} \\
\vdots \\
b_{n} \\
\end{matrix}
\right)
さて内積の最初の式から、$cosθ$を求めていきましょう。
\vec{a}・\vec{b} = |\vec{a}||\vec{b}| cosθ \\
\\
cosθ = \frac{\vec{a}・\vec{b}}{|\vec{a}||\vec{b}|}\\
\\
cosθ = \frac{a_{1}b_{1} + a_{2}b_{2}+ a_{3}b_{3} \cdots a_{n}b_{n}}{\sqrt{a_{1}^2+a_{2}^2 \cdots a_{n}^2} \sqrt{b_{1}^2+b_{2}^2 \cdots b_{n}^2} }
ここで、ベクトル$\vec{a}$と$\vec{b}$の長さがそれぞれ1だったら
cosθ = \frac{a_{1}b_{1} + a_{2}b_{2}+ a_{3}b_{3} \cdots a_{n}b_{n}}{1\times1}\\
\\
cosθ = a_{1}b_{1} + a_{2}b_{2}+ a_{3}b_{3} \cdots a_{n}b_{n}
となります。
ここで、話を単純にするために、$\vec{a}$と$\vec{b}$を二次元ベクトルで考えていきましょう。
長さが$1$の二次元ベクトルは、単位円で考えることができます
単位円
単位円は、「中心が原点$(0,0)$にある半径$1$の円」のことを言います。
このとき円周上の座標は、($cosθ$,$sinθ$)です。
ここで、単位円の円周上の点を幾つかとります。仮に$A,B,C$としてみましょう。
$A,B,C$の$x$と$y$の値は以下の通りとなります。
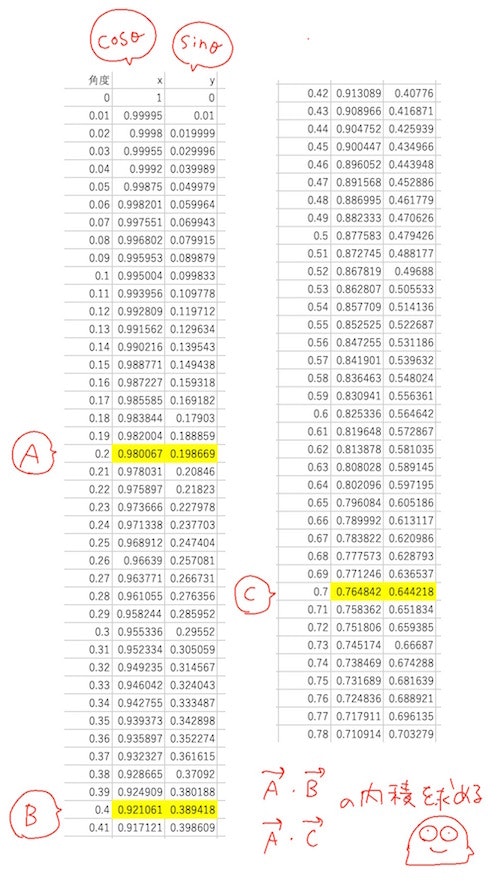
下の単位円の角度と$x$と$y$の値の表を参考にしてください。
$A$を角度$0.2$度とした場合、$x$と$y$の値は、$x=0.98 y=0.198$
$B$を角度$0.4$度とした場合、$x$と$y$の値は、$x=0.921 y=0.389$
$C$を角度$0.7$度とした場合、$x$と$y$の値は、$x=0.764 y=0.644$
では、$A$と$B$の内積と$A$と$C$の内積をそれぞれ求めてみましょう
\vec{A}・\vec{B} = 0.98 \times 0.921 + 0.198 \times 0.389 = 0.979602 \\
\vec{A}・\vec{C} = 0.98 \times 0.764 + 0.198 \times 0.644 = 0.876232 \\
$\vec{A}・\vec{B}$の方が$1$に近い数値が出ていますね。
さて、ここで$θ$の値が、$0^°$,$90^°$,$180^°$の時の$cos$の値を見てみましょう。
cos0^°=1 \\
cos90^°=0 \\
cos180^°=-1 \\
$cos0^°$というのは、2つのベクトルが同じ向きを向いているということになります。
この$cos0^°$の値が、$1$になります。
同様に$cos180^°$を考えると2つのベクトルは反対方向を向いていることになります。
この$cos180^°$の値が、$-1$になります。
つまり、内積の結果が$1$に近いほど、その2つのベクトルは同じ方向を向いているということになります。
上記で計算したベクトルの内積が、$\vec{A}・\vec{C}$よりも$\vec{A}・\vec{B}$の方が近いので、$1$に近い数値が出ていますよね。
まとめ
さて、ここまで説明してきたベクトルの内積の理論が、word2vecの中にあるというお話でした。
単語の意味をベクトルで表現するというのがword2vecの特徴ですが、これはつまり
東京 = {0.8, -0.01, 0.45, 0.23, ..... ,0.34, -0.56}
夜景 = {0.76, 0.71, -0.92, -0.86, ...., 0.45, 0.22}というように、それぞれの単語の意味をいくつかの数字の組み合わせで表す、ということです。デフォルトでは200個の数字の組み(=200次元)で表すように動作します。
引用元:word2vecのソースを読んでみた - Qiita
そのベクトルの内積をとって、$1$に近い数値の出る2つのベクトルは、関連性のある単語ということになります。
エピローグ
ぼへぼへは中学校まで数学のできる子だったのですが、高校生の時に、数Iで脱落してから、文系に進んだので、あんまり高校生の頃から数学をやった記憶がありません・・・(汗;
センター試験受験のために、必要な部分のみの数学を解答丸暗記方式で入試を乗り越えた後は、「学芸学部人間関係学科法社会学専攻」という数学と無縁な世界に行き、卒業後は、販売職、無職、ニート、営業、受付などを転々としていて、エンジニアになるとは思ってもいませんでした。そして再び数学が必要になる日が来るとは・・・
とあるきっかけで、エンジニアを志して、その仕事をやるようになってからが、数学的思考とか論理的思考とか諸々不足しつつ、走ってきたのですが、さて、機械学習がやってきてからは、生半可なぼんやり知識では入門書さえ読めないことに愕然としました。
機械学習の各種ライブラリを使うためには、すべての理論を知らなきゃ、ってわけではないですが、必要最低限って必要なのを痛感。
でも、実はドドドド文系でやってきたぼへぼへにとっては「必要最低限」のレベルが物凄く高いのです。
そんな人もたくさんいるかな、と思ってこのアドベントカレンダーを始めました。
やってみて初めて気付きましたが、これ書き手にとって、とても難しいカレンダーですね・・・。
普通に書くと、数学の教科書になるし、前提を吹っ飛ばしすぎるとわかりにくいし。
でも、何らか考えてアウトプットを出すという意味では良い機会になったかなと思います。
カレンダーに参加して、投稿してくれた皆様、ありがとうございます!
来年もがんばりましょう。
さて、明日は@hihatsさんです。よろしくお願いします!