\\
\begin{array}{l}
\lim_{x \to 0} \frac{\sin x}{x} = 1 の証明 \\
\\
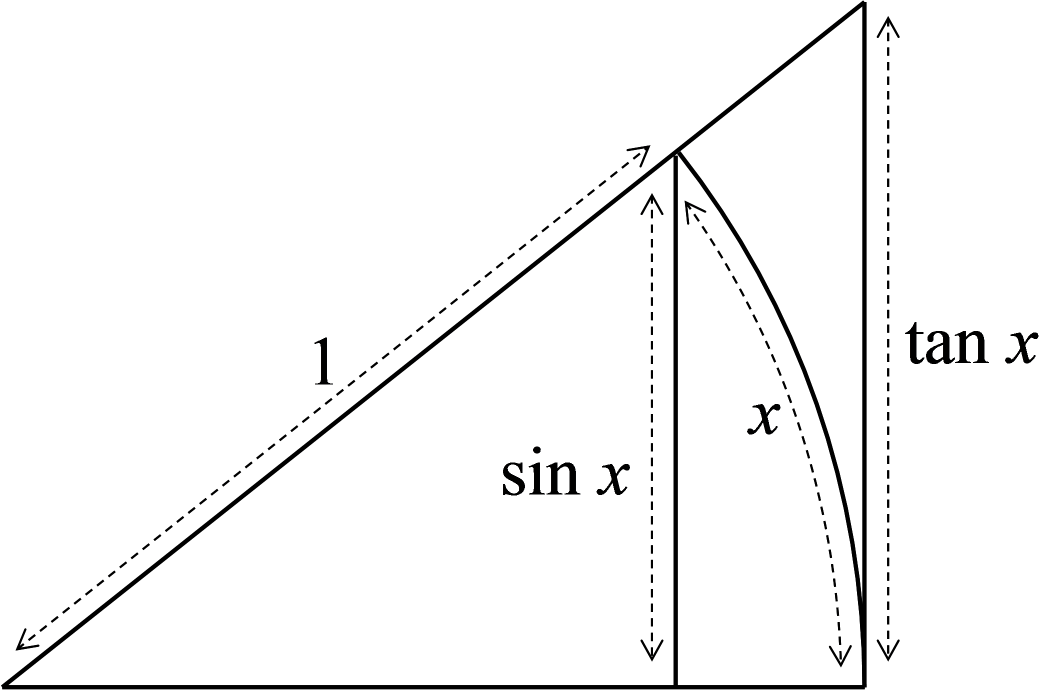
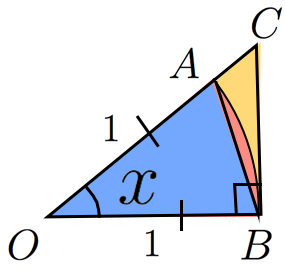
半径１で中心角が x ラジアンの扇形に内接する直角三角形と外接する直角三角形から考える。\\
\end{array}

\\
\begin{array}{l}
中心角が 0 < x < \frac{\pi}{2} のとき \\
\\
\begin{array}{rl}
1. &扇型に内接する直角三角形の面積（青色の部分） S_1 は、底辺=1、高さ=\sin x より\\
&S_1 = \frac{1}{2} \cdot 1 \cdot \sin x = \frac{\sin x}{2} \\
\\
2. &扇型の面積（青色＋赤色の部分） S_2 は、半径=1 で弧度法より、\\
&S_2 = \frac{1}{2} \cdot 1^2 \cdot x = \frac{x}{2} \\
\\
3. &扇型に外接する直角三角形の面積（青色＋赤色＋黄色の部分） S_3 は、底辺=1、高さ=\tan x より\\
&S_3 = \frac{1}{2} \cdot 1 \cdot \tan x = \frac{\tan x}{2} \\
\end{array}
\\
\\
面積から明らかに、 S_1 < S_2 < S_3 => \frac{\sin x}{2} < \frac{x}{2} < \frac{\tan x}{2} \\
\\
\\
\begin{array}{ll}
\frac{\sin x}{2} < \frac{x}{2} < \frac{\tan x}{2}　&全体に2をかける。\tan x = \frac{\sin x}{\cos x} \\
\sin x < x < \frac{\sin x}{\cos x} &0 < x < \frac{\pi}{2} より \sin x > 0 なので、\sin x で割って \\
1 < \frac{x}{\sin x} < \frac{1}{\cos x} &0 < x のとき逆数をとる \\
\cos x < \frac{\sin x}{x} < 1 &\\
\end{array}
\\
\begin{array}{rl}
\\
(1) &x > 0 のときに各辺に {x \to +0} の極限を取った場合\\
&\lim_{x \to +0} \cos x < \lim_{x \to +0} \frac{\sin x}{x} < 1 \\
&\lim_{x \to +0} \cos x = 1 より、1 < \lim_{x \to +0} \frac{\sin x}{x} < 1 \\
&はさみうちの原理より\\
&\lim_{x \to +0} \frac{\sin x}{x} = 1\\
\\
(2) &X < 0 のときに各辺に{x \to -0} の極限を取った場合\\
& x < 0 より -x > 0\\
&\cos x < \frac{\sin x}{x} < 1 に x = -x を代入して\\
&\cos (-x) < \frac{\sin (-x)}{(-x)} < 1\\
&\cos x < \frac{\sin x}{x} < 1\\
&各辺に{x \to -0} の極限をとると\\
&\lim_{x \to -0} \cos x < \lim_{x \to -0} \frac{\sin x}{x} < 1 \\
&\lim_{x \to -0} \cos x = 1 より、1 < \lim_{x \to -0} \frac{\sin x}{x} < 1 \\
&はさみうちの原理より\\
&\lim_{x \to -0} \frac{\sin x}{x} = 1\\
\end{array}
\\
\end{array}

\\
\begin{array}{ll}
&lim_{x \to 0} \frac{\tan x}{x} = 1 の証明 \\
\\
&\lim_{x \to 0} \frac{\sin x}{x} = 1 より\\
\\
&\lim_{x \to 0} \frac{\tan x}{x} \\
&= \lim_{x \to 0} \frac{\sin x}{\cos x} \cdot \frac{1}{x} \\
&= \lim_{x \to 0} \frac{\sin x}{x} \cdot \frac{1}{\cos x} \\
&= 1 \cdot \frac{1}{1}\\
&= 1\\
\end{array}

\\
\begin{array}{ll}
&\lim_{x \to 0} \frac{1 - \cos x}{x^2} = \frac{1}{2} の証明 \\
&\lim_{x \to 0} \frac{\sin x}{x} = 1 より\\
\\
&\lim_{x \to 0} \frac{1 - \cos x}{x^2} \\
&= \lim_{x \to 0} \frac{(1 - \cos x)}{x^2} \cdot \frac{(1 + \cos x)}{(1 + \cos x)} \\
&=  \lim_{x \to 0} \frac{1 - \cos^2 x}{x^2 (1 + \cos x)} \\
&=  \lim_{x \to 0} \frac{\sin^2 x}{x^2 (1 + \cos x)}　\because \sin^2 x + \cos^2 x = 1 => 1 - \cos^2 x = \sin^2 x \\
&=  \lim_{x \to 0} \left( \frac{\sin x}{x} \right)^2 \cdot \frac{1}{1 + \cos x} \\
&= 1^2 \cdot \frac{1}{1 + 1} \\
& = \frac{1}{2} \\
\end{array}