数学-三角関数-円周角の定理の証明

円周角の定理の証明

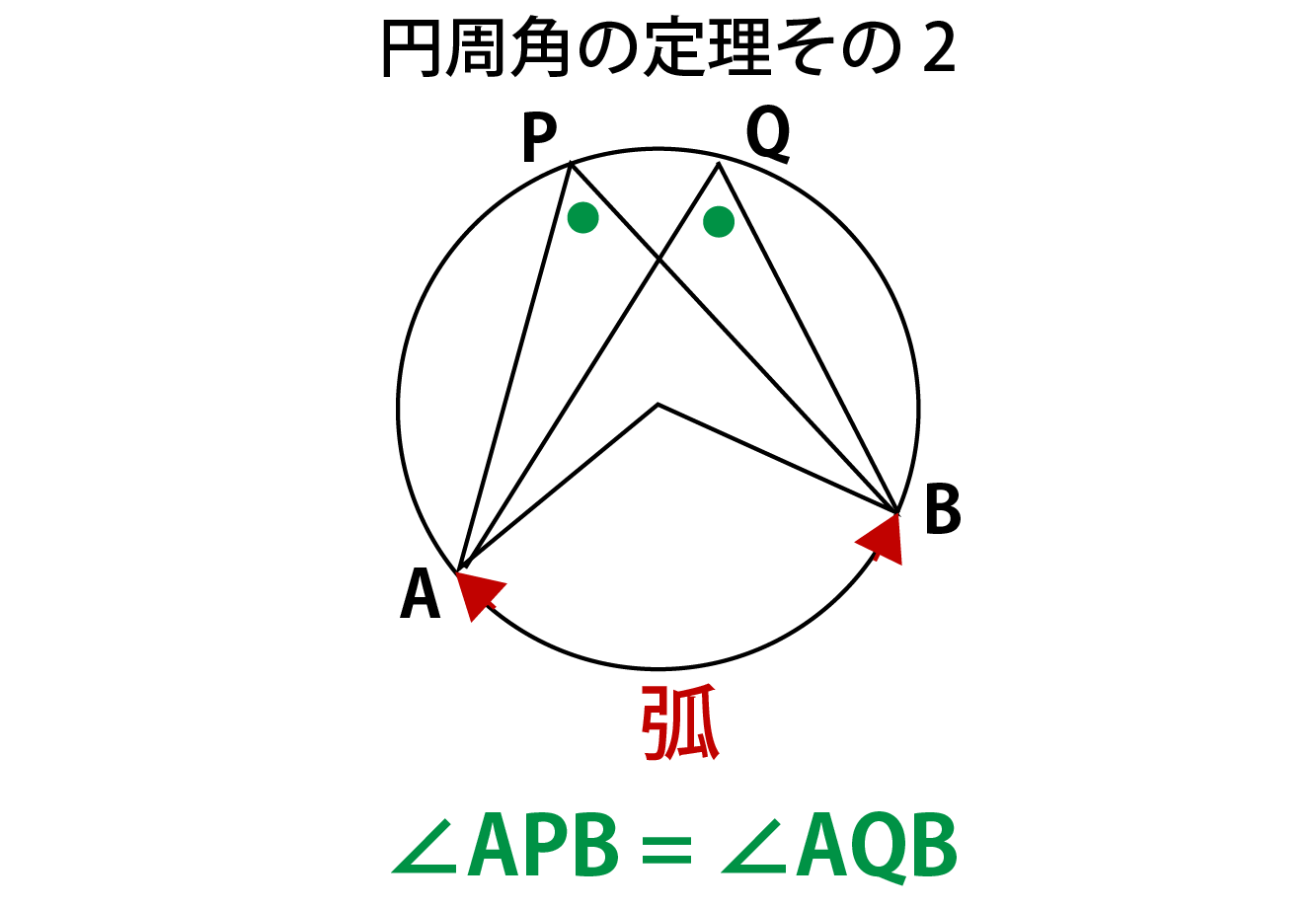
円周角の定理

• １つの孤に対する円周角の大きさは、中心角の大きさの半分になる

• 同じ孤に対する円周角は等しい

ACが円の中心を通る場合

OB と OC は円の半径だから、OB = OC\\
\triangle{OBC}は二等辺三角形になるので、\angle{OBC} = \angle{OCB}\\
　\\
\angle{AOB} + \angle{BOC} = 180^\circ (\because 直線)　①\\
\angle{OBC} + \angle{OCB} + \angle{BOC} = 180^\circ　 (\because \triangle{OBC}内角の和)　②\\
①②より、\angle{AOB} = \angle{OBC} + \angle{OCB} = 2 \angle{OCB} (\because \angle{OBC} = \angle{OCB})\\

円周角の内に円の中心がある場合

C から 円の中心 O を通る線を引き円との交点をDとする。\\
OA = OB = OC は円の半径だから、\triangle{OAC} と \triangle{OBC} は二等辺三角形になるので、\\
\angle{OAC} = \angle{OCA}\\
\angle{OBC} = \angle{OCB}\\
180^\circ = \angle{AOD} + \angle{AOC} = \angle{OAC} + \angle{OCA} + \angle{AOC} (\because \triangle{OAC}の内角の和)\\
よって、\angle{AOD} = \angle{OAC} + \angle{OCA} = 2 \angle{OCA}\\
同様に、\angle{BOD} = \angle{OBC} + \angle{OCB} = 2 \angle{OCB}\\
　\\
\angle{AOB} = \angle{AOD} + \angle{BOD} = 2 \angle{OCA} + 2 \angle{OCB} = 2 (\angle{OCA} + \angle{OCB}) = 2 \angle{ACB}\\

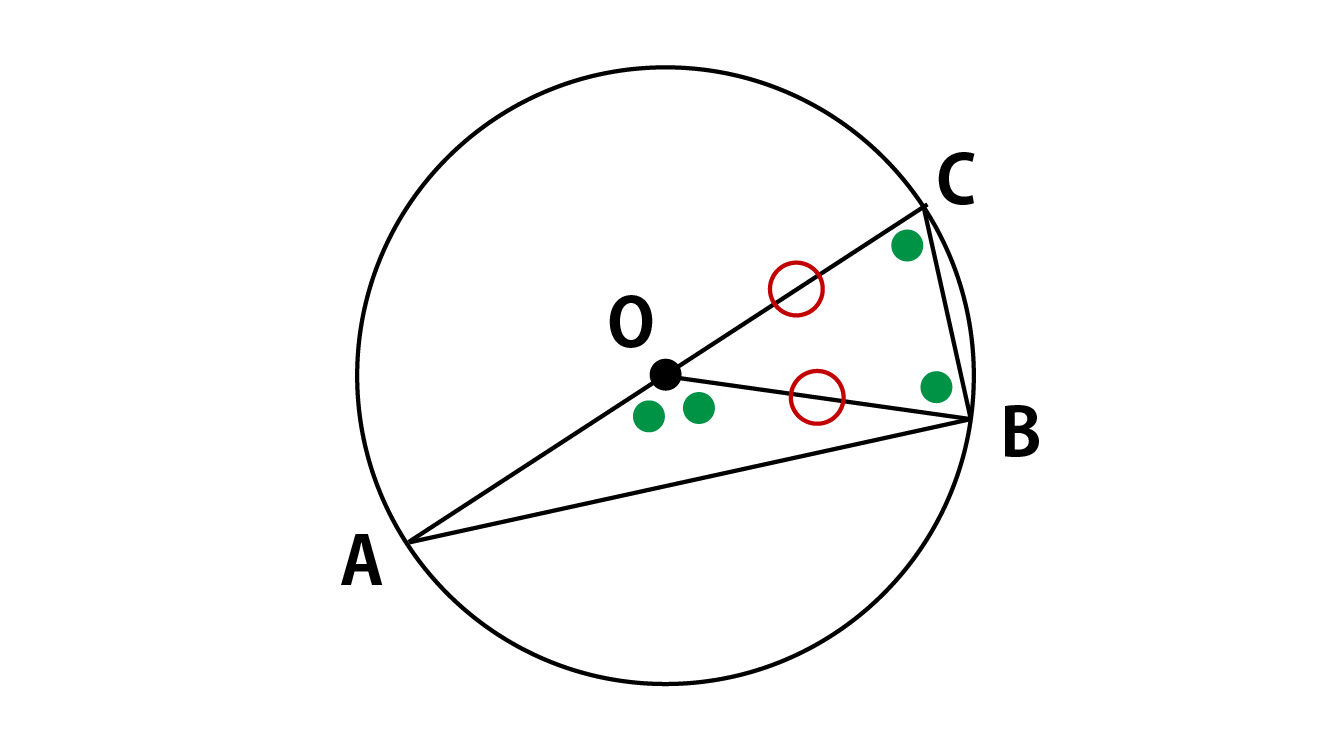
円周角の外に円の中心がある場合