はじめに
UKIです。久しぶりの記事執筆となります。
本記事は、仮想通貨botter Advent Calendar 2023の1日目の記事となります。
本記事の目的
仮想通貨botterと言っても様々なスタイルがあります。
筆者のbotスタイルは、「主に流動性の高いCEXにおいて、価格の上下を予測してトレードする」というオーソドックスなスタイルです。価格予測には単純なルールベースを使うこともありますが、最近ではガッツリ機械学習を用いてこれを予測することが多くなってきています。
さて本題に入りますが、皆さんは機械学習で価格予測モデルを構築するとき、「回帰問題」とするか「分類問題」とするか悩んだことはないでしょうか。
本記事では、トレーディングの効用を最大化するために、機械学習の問題設定をどのようにすべきか論じます。
参考書籍・参考文献
今回の記事では上記の書籍を参考としました。
この書籍中には、ビジネスの効用(KPI)を最大化するために機械学習の問題設定や損失関数の選定をどのように行えばよいか、いくつかの事例が紹介されています。本記事の考え方もこの書籍を参考として導出しました。
Amazonのレビューでは辛口なコメントが付いていますが、Twitterで検索してみるとポジティブな意見が多いです。初級者向けに非常に良い書籍だと筆者も考えています。
また毎回紹介していますが、マーケット予測のための問題設定については以下の記事が非常に有用なので、一読することをお勧めします。
お断り
本記事の内容ですが、考え方の一例として捉えて頂き、読者の方も独自に発展させてもらえれば幸いです。内容について是非ご意見いただけたらと思います。
トレードの意思決定とKPI
まず、トレードにおいて我々ができること、そしてその目標(どうなればよいか)について整理しましょう。
トレード対象となるアセットの選定は完了しているものとすると、トレードにおいて我々ができること(意思決定)は、
- 買うか、売るか、何もしないか。
- 買う(もしくは売る)ならどれだけ買うか
細かく言えば、執行方法を成行にするか指値にするか、約定を急ぐか急がないか等も考えることができますが、まず問題は可能な限り単純化して考えます。
続いて目標の定義として、トレードの効用を考えます。ここでは参考書籍に則ってKPI(Key Performance Indicator:重要達成度指標)という言葉を使います。トレードのKPIとして以下のようなものが考えられます。
- 最終的な利益の絶対額
- 運用中の最大DD
- シャープレシオ
KPIの最大化を考える
本記事ではKPIを以下のように損益の総和として定義し、問題設定としてその最大化について考えることにします。
\mathrm{argmax} \ KPI = \mathrm{argmax} \sum_{i=1}^{n} PNL_i
この式における$PNL_i$は、以下の式で記述することができます。
\ PNL_i = rt_i \times position_i
ここで、右辺第1項はアセット自身の値動きであり、正負の値を取ります。第2項はトレーダーの取りうるポジションの値であり、取引所のレバレッジ上限を$L$とすると、$position_i \in (-L, L) $となります。
$position_i=1$のとき、レバレッジ1倍でロングポジションを持つことに相当し、$position_i < 0$のときはショートポジションを持つことに相当します。$position_i=0$はいわゆるノーポジです。
さて、さらに条件を追加で定義します。今トレーダーは、期間$i$における値動き$rt_i$の予測として$\hat{rt_i}$の情報を所有しており、$\hat{rt_i}$の正負に応じてレバレッジ1倍のロングポジションもしくはショートポジションを持つものとします。この条件を数式で表すと、以下のようになります。
\ position_i = \mathrm{sign}(\hat{rt_i})
この式を$PNL_i$の式に代入すると、
PNL_i = rt_i \times \mathrm{sign}(\hat{rt_i}) = |rt_i| \times \mathrm{sign}(rt_i) \times \mathrm{sign}(\hat{rt_i}) = |rt_i| \times \mathrm{sign}(rt_i \times \hat{rt_i})
まず右辺第2項である$\mathrm{sign}(rt_i \times \hat{rt_i})$は「符号的中率」と呼ばれる項です。どれくらい近い数値を予測したかではなく、正負の符号が的中したかどうかを表す項となります。$KPI$を向上させるためには、まずこの「符号的中率」を向上させることを考える必要があります。
続いて第1項は、期間$i$における値幅の大きさを示します。$PNL_i$は値幅と符号的中率の積となっており、当然ですが値幅が大きいときに予測を的中することができれば$KPI$をより向上させることができます。ここで、アセットの値幅がどれだけ出るかは売買の意思決定とは無関係です(ただし相場操縦を除く)。
値幅の大きいときに的中できれば$KPI$は高くなるため、これを評価に取り入れて重み付き符号的中率を向上させるほうがよりパフォーマンスが向上できると考えられます。ただし、このウェイトはトレード開始する時点では未知の項であるため、市況や直近の値幅からこれを概算で推定することになります。
問題設定を考える
上記のとおり、$KPI$を向上させるためには、符号的中率を向上させる必要があります。絶対値の予測は必要なく的中率の向上が目的となるため、問題設定として考えられるのは回帰問題ではなく分類問題となります。このように、意思決定がロングorショートのように離散化している場合、回帰問題は不適であると言えるでしょう。
二値分類問題を考える
ターゲットを上昇or下落の二値として分類問題を解きます。
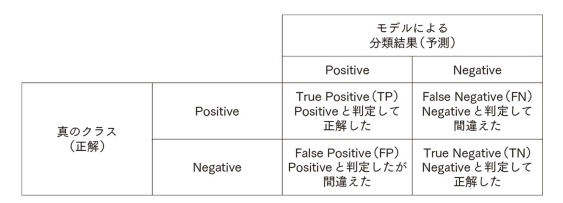
ここで符号的中率を上げるためには、機械学習の評価指標はどのようなものにすればよいでしょうか。二値分類における符号的中率とは、すなわち「正解率(Accuracy)」と同義です。
参考:二値分類問題の評価指標
正解率(Accuracy)
$Accuracy = \frac{TP+TN}{TP+FP+FN+TN}$適合率(Precision)
$Precision = \frac{TP}{TP+FP}$再現率(Recall)
$Recall = \frac{TP}{FN+TP}$その他にもF1-score、ROC-AUCなどがあります。
正解率の分子はTrue PositiveとTrue Negativeを合わせたものであり、これは的中率と同義となります。
二値分類の「正解率」を上げるために損失関数として選定されるのはBCE Loss(Binary Cross Entropy Loss)となります。BCE Lossは以下の式で表されます。ここで$y_i$はサンプル$i$がラベル1を取る真の確率、$p_i$は予測した確率となります。
BCE Loss = -\sum_{i} (y_i \log(p_i) + (1 - y_i) \log(1 - p_i) )
今回はハードラベル(正解ラベルには確率1、それ以外のラベルには確率0が付与されるラベル)であるため、BCE Lossには偽ラベルの予測確率は考慮されません。BCE LossにはTPとTNの予測確率のみが計上されることになり、損失関数を下げる一連の所作が正解率を向上させることに直接繋がります。
重み付き的中率を最大化する
上記は通常のBCE Lossですが、理論的には「重み付き的中率」を最大化するほうがより効率的です。これにはBCE LossのWeightを使います。例えばPytorchのBCE Lossには、引数でWeightを設定できるようになっています。

引用元:Pytorch.org
このウェイトは、サンプル毎に設定することになります。
前述したように値幅の出るところで的中率を上げたいため、このウェイトはボラティリティの関数にすることが第一に考えられます。
サンプルを絞る手法
極端な話をすると、weightの与え方として対象トレードのweightを1、非対象トレードのweightを0と設定する場合を考えることができます。例を挙げると、ボラティリティや市況によってトレード対象を絞り込むような場合です。
「重み付き符号的中率を最大化する」といった理論に則った場合、このようにスクリーニングしたサンプルに対して二値分類を行うことは、理にかなった手法であると言えるでしょう(ただし十分なサンプル数を確保する必要があります)。
三値分類(多値分類)
三値分類を行う場合は-1, 0, 1のようなラベルを付与することが一般的ですが、このラベルは予め値幅の大きさによって分類されているため、大雑把な重み付けがされていると考えることができます。重み付き的中率を向上するためには、True PositiveとTrue Negativeの割合を上げればよいことになります。

引用元:筆者作成
この問題の損失関数にはCross Entropy Lossを使います。
Cross Entropy Lossでは、True PositiveとTrue Negativeに加えて、True Neutralの予測確率も損失に計上することになります。もしもTrue PositiveとTrue Negativeの的中率に大きなウェイトを置きたい場合には、各ラベルの確率値を調整する等の所作で実現することができます。
三値分類でペナルティを考える
三値分類のラベル1およびラベル-1の予測において、強いFalse Positiveもしくは強いFalse Negativeとなってしまった場合、実際の運用で大きな損失を被ることになります。Cross Entropy Lossでは、正解ラベルの予測確率のみ使ってLossを算出するため、弱いFalse Posiviteであるか強いFalse Positiveであるかは区別されず、強いFalse Positiveとなった場合のペナルティが考慮されていません。これにはカスタム損失関数を使って評価することが考えられます。
問題設定のまとめ
以上をまとめると、トレーディングのための機械学習の問題設定および損失関数の選定は、以下のような形が望ましいと考えられます。
- 二値分類問題として、損失関数に重み付きBCE Lossを用いる。
- 二値分類問題として、あらかじめスクリーニングしたサンプルについて通常のBCE Lossを用いる(ただし十分なサンプル数が残る必要がある)
- 三値分類問題として、Cross Entropy Lossを用いる
- 三値分類問題として、カスタム損失関数で強いFalse Positiveにペナルティを与える
実証結果
以下の内容について、モデルのパフォーマンスを比較しました。
- 二値分類 + BCE Loss
- 二値分類 + 重み付きBCE Loss
- サンプルスクリーニング後、二値分類 + BCE Loss
- 三値分類 + Cross Entropy Loss
- 三値分類 + カスタム損失関数
- さらに多値分類 + Cross Entropy Loss
もうサラッと結論だけ書いてしまいますが、筆者の検証では「さらに多値分類 + Cross Entropy Loss」のパフォーマンスが最も優れていました。またカスタム損失関数でペナルティを与える仕様にした場合、モデルは消極的な予測ばかりするようになり、うまく学習することができませんでした(ニュートラルしか予測しなくなる)。
おわりに
まとめですが、
- 的中率が重要である。特に、値幅の広くなるところで的中率を上げる必要がある。
- 二値分類よりも多値分類のほうがよい。これは、多クラス分類してそれぞれのクラスの予測精度を上げるという行為が、重み付き的中率を上げるという目的を暗に達成しているものと考える。
- 強いFalse Positiveにペナルティを与えると、消極的予測しかしなくなる。
特徴量やモデルが変わると必ずしも同じ結果になるとは限りませんので、ご自身で確認いただくのがよいと思います。
また今回の記事では条件を可能な限り単純化して考えましたが、数式の得意な方はさらに難しいKPIやポジションの取り方について、問題設定を考えてみるのも面白いと思います。
それではまた次の記事で会いましょう。