はじめに
本記事は、MediumのTowards Data Scienceに寄稿した「Numerai Tournament: Blending Traditional Quantitative Approach & Modern Machine Learning」を和訳したものである。
Numeraiトーナメントについて
Numeraiはクラウドソーシング型ファンドと呼ばれる、不特定多数の人間による株価の予測結果をもとに運用するヘッジファンドである。Numeraiでは予測性能を競うトーナメントが開催される。トーナメント参加者はNumeraiから提供されるデータセットを元に予測モデルを構築し提出を行う。参加者はその予測性能に応じてランキングされ、報酬が支払われる(徴収されることもある)。
Numeraiへの出資者には、ルネッサンス・テクノロジーズの共同創業者であるハワード・モーガン、チューダー・インベストメンツの創業者であるポール・チューダー・ジョーンズ、米国老舗のVCであるユニオン・スクエア・ベンチャーズ、その他の著名なVCやヘッジファンド経験者が含まれており、データセットはファイナンスM/L専門のアドバイザーに監修されている。これまでに参加者に支払われた賞金総額は3400万ドルを超えており、プロジェクトの進捗は良好だと推察される。

(イメージ:Numerai提供)
筆者について
筆者はマーケットニュートラルと呼ばれる手法を用いて日本株で資産運用を行っている。マーケットニュートラルとは、ユニバース内(投資対象となる銘柄群)における株価の相対的な騰落を予測し、買いと売りを組み合わせて市場の値動きに依存しない絶対的リターンを狙うものである。筆者は伝統的なクオンツ手法と統計学をベースとし、機械学習を使ってこの株価予測モデルを構築している。運用結果は良好でありその利回りはおよそ40%となっている。
本記事の目的
本記事では、筆者の運用モデル構築の過程において得た知見を共有する。まず伝統的なクオンツ運用の考え方を説明し、それを機械学習とブレンドして最新の予測モデルを構築するための方法を論じる。
注記
Numeraiのデータセットは難読化されており、筆者はこれに対して何らインサイダー的な情報を持ち合わせていない。本記事の内容は筆者の投資およびモデリングの経験による独自の視点によるものである。
伝統的なクオンツ手法
株式リターンの予測に関する研究は古くから行われている。まずは伝統的なクオンツ手法とはどのようなものか、その生い立ちから説明していこう。
BARRAのリスクモデル
現在のクオンツの原型となったのはバー・ローゼンバーグが提唱したリスクモデルだろう[1]。これには諸説あるが、このあたりのウォールストリートの歴史を知るためにはピーター・バーンスタインの著書Capital Ideas(邦訳版タイトル「証券投資の思想革命」)を是非とも読むべきだろう[2]。
1960年代、ローゼンバーグはマーコヴィッツの共分散モデルを元に、個々の企業のリスクを様々な要因を用いて説明する手法を考案した。そしてこれらのリスク要因が、株価の超過リターンに結びついていることを発見した(リスク・プレミアム)。1975年、ローゼンバーグはコンサルティング会社であるバー・ローゼンバーグ・アソシエイツを設立する。この会社はBARRAとして世界中の運用会社に知られることになった。
現在では、BARRAモデルは最も有名なリスクモデルであり、MSCIがベンダーとしてこれを提供している。他のリスクモデルにはAxiomaなどがある。BARRAモデルには様々な種類のモデルがあるが、BARRA Global Equity Model(GEM)は世界中の主要な株式市場の株式を対象としたリスクモデルである[3]。このモデルでは、株式のリターンを以下のようにカントリー要因、産業要因、リスク要因、個別要因に分解している。

これを重回帰モデルで記述すると以下のようになる。Rnは銘柄nの(リスクフリー金利に対する)超過リターン、xは銘柄nの各ファクター(k、j、i)へのファクターエクスポージャー、fはファクターリターン、enはスペシフィックリターンである。ここで重要なのがファクターリターンの考え方である。

ファクターリターン
簡単のため、マルチファクターモデルではなくシングルファクターモデルで説明する。また、具体例としてNumeraiのデータセット構造で説明を進める。ファクターリターンとは、以下のクロスセクション回帰における、回帰係数fを示す。rはeraXにおけるターゲットベクトル、xはeraXにおけるfeatureAのベクトルである。
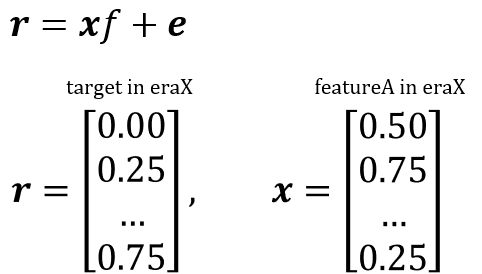
ファクターリターンとは、そのユニバースにおいてそのリスクファクターにベットするとどれくらいのリターンが見込めるか、という指標である。またファクターエクスポージャーとは、その銘柄がそのリスクファクターに対してどれだけ曝されているか(exposeされているか)を示し、これが大きいほどファクターリターンから得られる恩恵が大きくなる。上の式を見ると分かるように、この回帰モデルは特定の期間(eraX)におけるクロスセクションなモデルであり、実際の検証ではこれを期間毎(例えばマンスリー)に時系列に積み上げてその特徴を観察することになる。
以下にBARRA GEMの資料からファクターリターンを一部抜粋した。ファクターリターンが顕著に右肩上がりで推移するものは、そのファクターにベットしてさえおけば安定してリターンを得ることができる、ということである。逆に顕著に右肩下がりになるのであればそのファクターに逆にベットすればよい(ロングとショートを入れかえる)。現在の2020年においてファクターリターンが一方向に顕著に推移するものは少ない。従って各銘柄のファクターエクスポージャーを念頭に置いて様々なファクターに分散してベットできるようポートフォリオを組むのである。
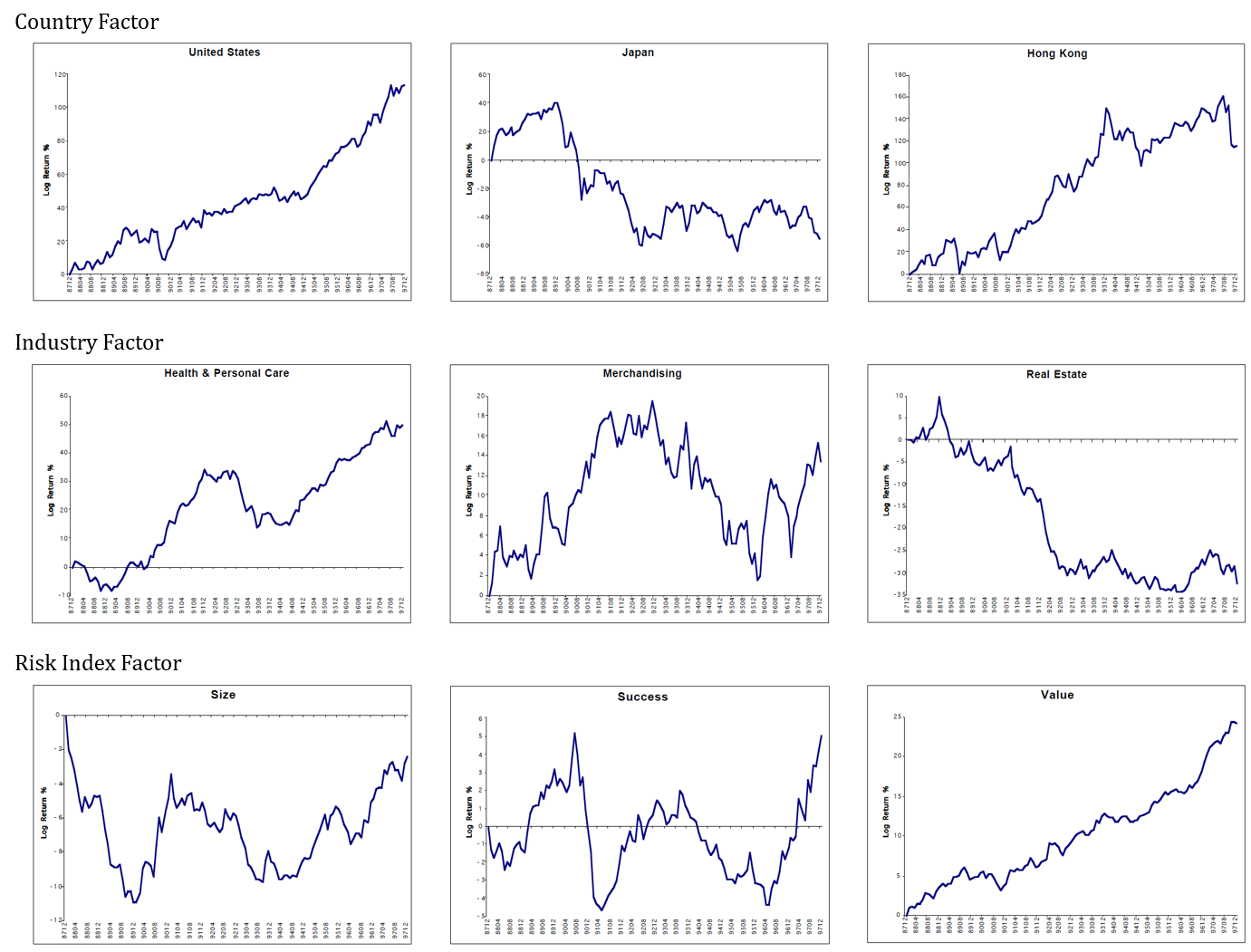
(図:文献[3]より筆者作成)
ファクターリターンとCorrelationの関係
ファクターリターンは回帰係数であるので、目的変数および説明変数のボラティリティを用いてCorrelationに変換することができる。下の式で、bは目的変数yに対する説明変数xの回帰係数、σxyはxとyの共分散、σxとσyはそれぞれxとyの標準偏差である。Correlationとは、ファクターリターンである回帰係数をボラティリティで補正して-1~1の間に規格化したものなのだ。
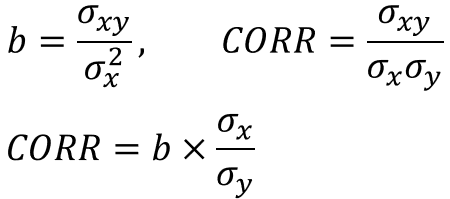
Correlationはリスクモデル、ひいてはアクティブ運用理論で非常に重要な指標である。アクティブ運用理論ではCorrelationはInformation Coefficientと呼ばれ、投資家のスキルを示す指標となっている。このあたりの詳細説明は割愛する。興味のある方は、アクティブ運用理論で最も有名な書籍を参照してみるとよい[4]。
ここではNumeraiの各featureのファクターリターン(Correlationで計算)を記載した。マルチファクターではなく単純にシングルファクターで計算している。この図から、どのFeatureがどのような特徴を持ち、それ自体でどれだけ説明力を持っているのか一目で判別できる。
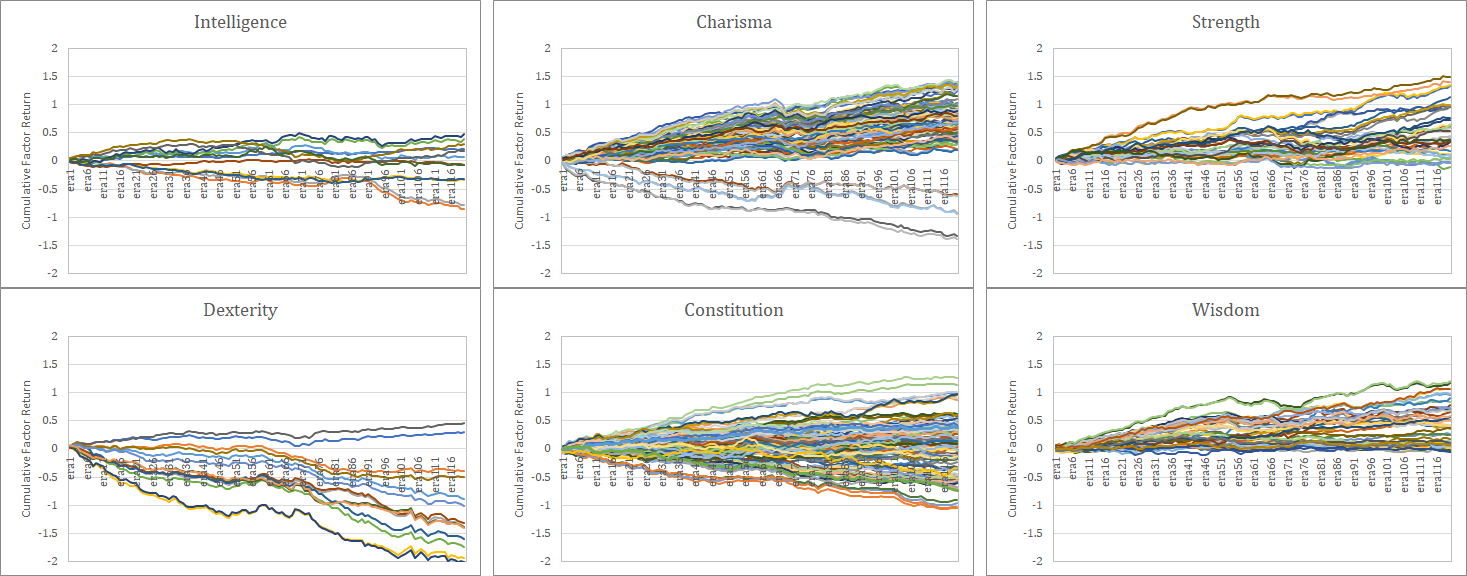
なお、これらのファクターリターンはランダムネスによるバラツキを含んでいることに注意が必要である。以下はCorrelation=0.0の場合とCorrelation=0.005の場合のモンテカルロシミュレーションである(100回試行)。ランダムネスでこの程度のバラツキが発生することは、常に頭に入れておくべきである。サンプル期間120程度で統計的な有意性を判断することは非常に難しい問題なのである。なお、ファクターリターンが最も顕著に推移しているのは、当然ながらdexterity4と7である。
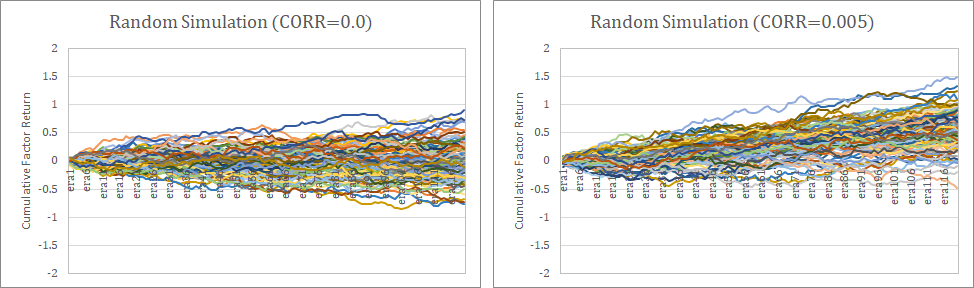
Correlationによる評価について
このように考えると、NumeraiがなぜCorrelationで評価を行うか分かるだろう。我々トーナメント参加者1人1人が提出したpredictionは、それ自体がNumeraiにとって既存の特徴量よりも情報を含んだ1つ1つのファクターなのである。Numeraiは参加者が独自に生み出した優秀なファクターリターンを募っているのだ。ファクターリターンが優秀であれば、Numeraiは単純にそれを組み合わせるだけで運用しても良いし、場合によっては性能を高めるために集まった個々のファクターをさらに学習に掛けてもよいのである。
Featureとしてのリスクファクター
本章では、機械学習のために従来のリスクファクターをfeatureとして取り込むのであればどのようになるか考察する。まず重要なのはCountry featureとIndustry featureである。
Country Feature
Numeraiでは世界中の主要市場における株式をユニバースとしていると考えられる。Numeraiトーナメントのデータでは個別銘柄のidは暗号化されており、これを知る術はない。しかしNumerai Signalsにおいて対象銘柄リストが公開されていたのでそれを集計してみた。銘柄数からして現在のNumeraiトーナメントと同じではないかと睨んでいる。Numerai Signalsの銘柄は41ヵ国であり、最も多い国はUS、その後日本、韓国、英国と続く。これらは単純にCountryとして取り込むのではなく、Regionとしてfeatureに取り込む可能性も考えられる(North America、South America、Pacific、etc)。

通常のリスクモデルでは、Country featureは0/1のカテゴリ変数として導入される。ところがNumeraiのデータセットは基本的に5分位であり、且つそれぞれの分位の銘柄数は揃っていることが多い。従ってこのようにfeature化するのであれば、もしも自分であれば各Country(もしくは各Region)のインデックスに対する重回帰を行い、そのベータを特徴量として分位分けする。
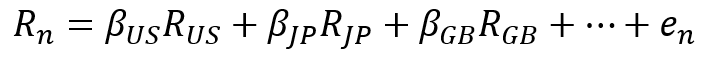
例えばこのような所作を行うと、日本の銘柄は東証のインデックスに対してベータが大きくなり、そのfeatureにおける大きな分位に集まることになる(もしくは分類の符号によっては小さな分位に集まる)。そうするともしCountry featureが存在しているのであれば、重要なのは一番端の分位であって、それ以外は情報として不要な分位となるわけだ。Numeraiのanalysis_and_tipsには特徴量の数値が0もしくは1で極端に特徴が現れるという報告があったが、これはこういう可能性があると考えている。
参考までに2010年以降の各国のレラティブリターン推移を示す。
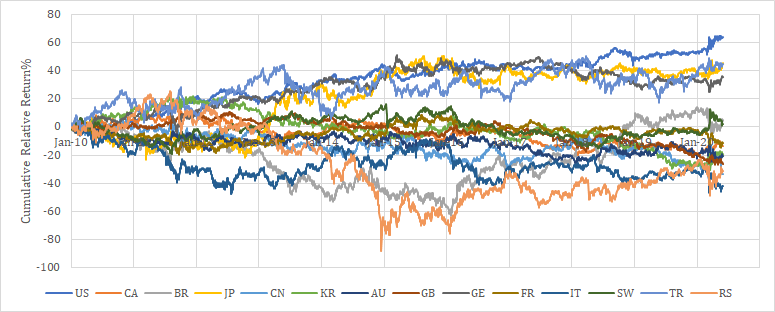
Industry Feature
次に重要なのがIndustry featureである。マーケットの魔術師において、スティーブ・コーエンは株価の動きを形成するのは40%がマーケット、30%が業種、残りの30%が個別要因だと述べている。このfeatureが取り入れられていないはずがないのである。業種の定義は様々であるが、BARRA GEMでは38の業種が定義されている。その他にも、GICSでは60セクターが、FactSetの提供しているRBICSでは12のEconomy、31のSector、89のSubsectorが定義されている。参考までにUS市場におけるEconomy別の銘柄数を示しておく。
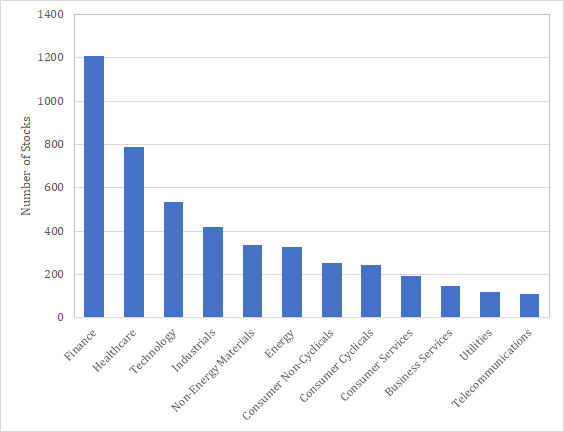
IndustryもCountryと同様に業種インデックスに対する重回帰ベータを特徴量として分位分けされている可能性がある。この場合も重要なのは一番端の分位であって、それ以外は情報として不要な分位となる。
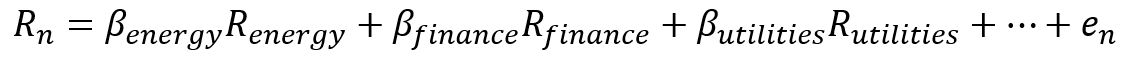
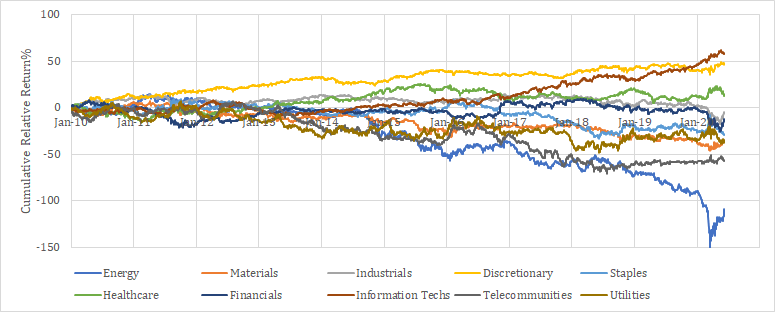
参考までに2010年以降のUS市場の各業種のレラティブリターン推移を示す。
Risk Index Feature
Risk Indexには、BARRAで使われているものは取り込まれている可能性が高い。サイズ、バリュー、サクセス(モメンタム)、ボラティリティである。これらは単純に取り込むこともできるが、CountryやIndustryなどの区分によるバイアスを考慮して正規化する場合が多い。
サイズであれば、時価総額だけでなく、売上高、総資産、従業員数などのファクターも考えられる。バリューであれば、PBR、PER、PCFRなどが考えられる。
その他のRisk Indexとして、流動性、グロース、配当、財務レバレッジ等がある。またこのような伝統的なRisk Indexだけでなく、アナリスト情報やニュースから抽出したセンチメント指数などの代替変数も取り込むことができる。
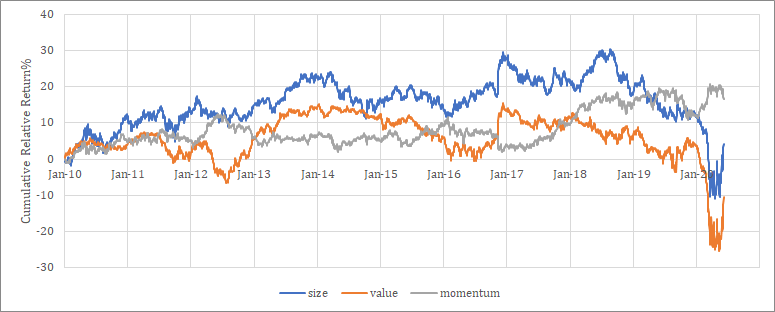
参考までに2010年以降のUS市場の各Risk Indexのレラティブリターン推移を示す。
伝統的なクオンツと機械学習の融合
本章では、伝統的なクオンツに対して機械学習を用いることでどのようにパフォーマンスが改善できるか、その方法論を述べる。
ツリーモデル
Barraモデルは単純に個々のリスクファクターの加重平均である。これをもう少し発展させる単純で簡便な方法が存在する。それが交互作用を取ることだ。簡単な例を挙げると、バリューが効きやすい業種とそうでない業種がある。また業種ではなく銘柄の規模を例に取ると、大型株で効きやすいファクター、小型株で効きやすいファクターがある。さらに国によって異なる業種がアウトパフォームする。このような交互作用を考慮するためには、線形モデルは不適当である。線形モデルでは交互作用の項を人間が指定してfeatureとして設定する必要があるからだ。ツリー系の手法であれば特に意図しなくともモデルが独自に交互作用を学習することができる。一方で、ツリー系の手法は格子状の分割となるため線形の分類が苦手であり、もともとのBARRAモデルのリスクプレミアム自体を理解することは不得意である。
これを解決するのが、線形モデルとツリーモデルのアンサンブルやスタッキングである。実際にKaggleで行われたツーシグマのコンペティションでは、線形モデルであるRidge回帰とツリーモデルであるExtraTreesのアンサンブルが上位入賞している[5]。
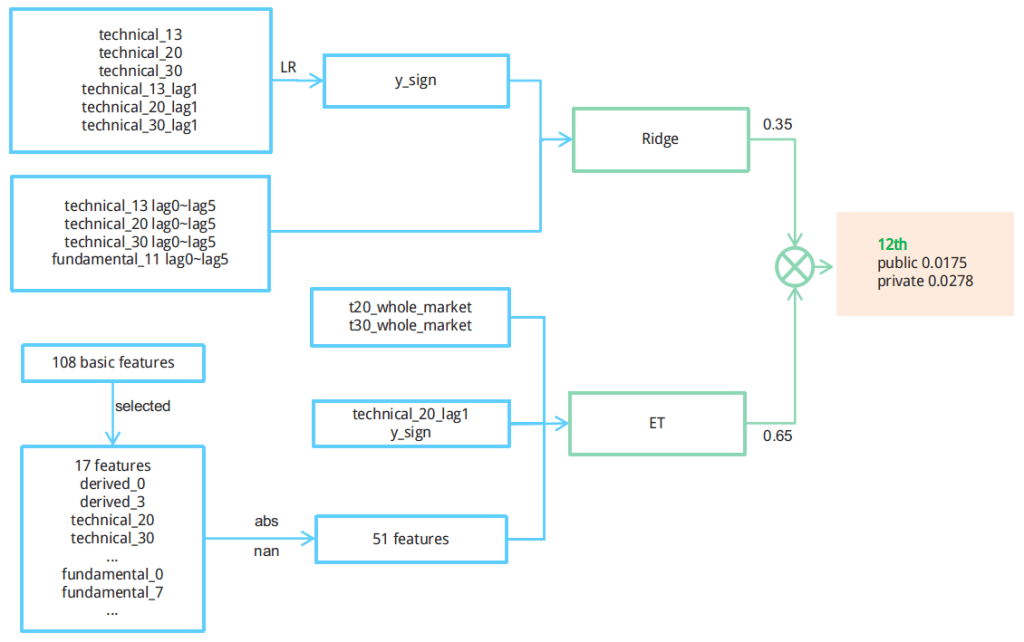
(図:文献[5]より)
Deep Factorモデル
一方でモデルにディープラーニングを用いる事例もある。これはDeep Factorモデルと呼ばれる手法である[6]。従来のクオンツ運用では、ファクターの作成から選定までを運用者であるファンドマネージャーが経験に基づいて行っていたが、Deep Factorモデルではこれをディープラーニングに置き換えることで人間の判断を排除して個々のファクターの持つ非線形性を捉えることを目的とする。
この手法では80個のファクターを用いて月次リターンを予測しており、線形モデルや他の機械学習手法(SVRやランダムフォレスト)による予測をアウトパフォームできることが確認されている。
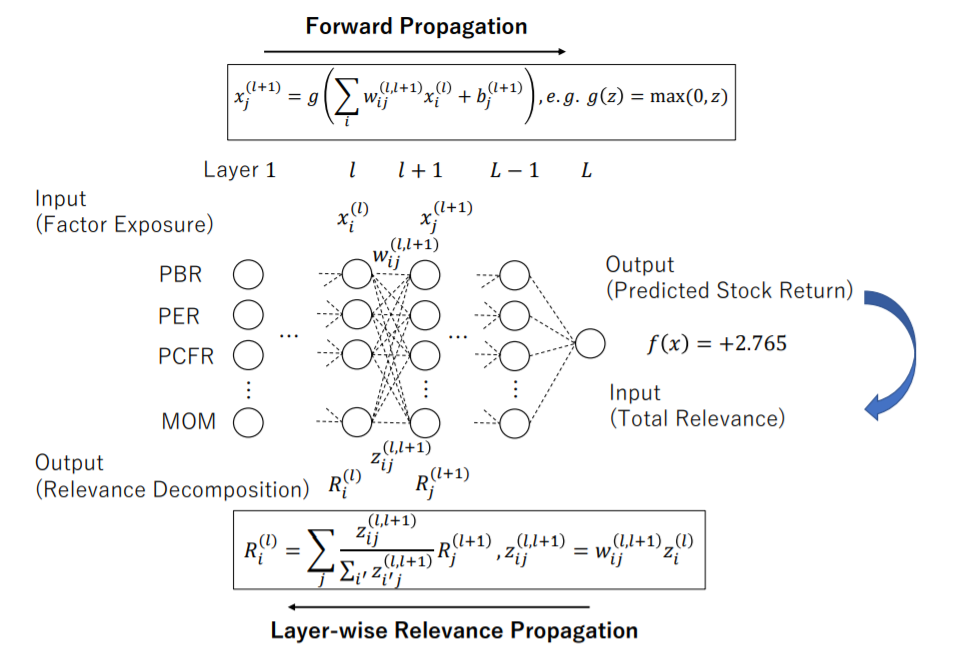
(図:文献[6]より)
このように機械学習を用いることで、伝統的なクオンツモデルを凌ぐことは比較的たやすいものと考えている。ただし、一方でモデルが複雑になることによる可読性の低下や、過学習やスヌーピングバイアスなどの落とし穴もあるため、モデルの構築にはFinance分野特有の知識や勘所が要求される。このあたりの技術的なテクニックについては、NumeraiのアドバイザーであるPrado氏の著書であるファイナンス機械学習を参考とすべきである[7]。
おわりに
本記事では、伝統的なクオンツ運用の考え方を説明し、従来のリスクファクターをfeatureとして取り込む手法を述べ、従来のクオンツと機械学習がどのようにブレンドされるのか説明した。伝統的なクオンツは最新の機械学習とブレンドされることで、より一層と実運用におけるパフォーマンスを改善できる可能性があることがご理解いただけただろう。
また読者の方には、従来のクオンツの考え方に基づく市場の観察方法を知っていただくことで、より実際の市場に興味を持っていただければNumeraiでの分析がさらに楽しいものとなるはずだ。本記事が読者の方の好奇心を刺激し、モデルにインスピレーションを与えることを願っている。最後まで読んで頂き、感謝する。
謝辞
本記事の執筆にあたり、Numerai運営様に画像の提供、文章の校正にご協力頂きました。この場を借りて御礼申し上げます。
参考文献
[1]Barr Rosenberg, Marathe Vinay, "The prediction of investment risk: Systematic and residual risk", 1975
[2]Peter Bernstein, "Capital ideas: The improbable origins of modern Wall Street", 1992
[3]Barra global equity model handbook
[4]Richard Grinold, Ronald Kahn, "Active portfolio management", 1995
[5]Team Best Fitting, "Two Sigma Financial Modeling Code Competition, 5th Place Winners’ Interview", 2017
[6]Kei Nakagawa, Takumi Uchida, "Deep Factor Model: Explaining deep learning decisions for forecasting stock returns with LRP", 2018
[7]Marcos Lopez de Prado, "Advances in financial machine learning", 2018