はじめに
ちょうど3年ほど前に機械学習による株価予測のTipsをブログにて公開したことがある。
機械学習による株価予測には押さえておくべきノウハウが多数あり(要するにドメイン知識が必要であり)、データサイエンティストが単に予測対象を株価に置き換えても簡単に良い結果を得ることは難しい。フィナンシャルデータは過分散で統計的エラーが発生しやすく、バックテストや検証の結果は殆どの場合で信用するに値しない。その上、取引における市場の仕組みや制度を正しく検証に反映できていない場合、実運用において大きくパフォーマンスが劣化してしまう。考慮すべき事象は、上場情報(新規、廃止、監理指定等)、取引規制や貸借情報(売買停止、空売り規制、信用取引規制等)に加え、売買のレイテンシー、板の厚みやキューの考え方など多岐に渡る。
このため殆どの検証は机上の空論で終わる可能性が高い。検証に関する記事は多数存在するが、実弾投入したときのパフォーマンスを載せているものは殆ど見掛けない。機械学習による株価予測は殆どの場合で失敗に終わるため、正直なところ流行しないものと考えていた。しかし最近になってフィナンシャルデータの機械学習に関する書籍がいくつか出版されている。もしかするとそれなりにニーズがあるのではと考え、今一度、機械学習による株価予測のTipsについてもう少し深堀りしてまとめてみたいと思った次第である。
なお、筆者は自身で構築した機械学習モデルを元に日々株式を売買しており、ここまでの累積利益は9000万を超えている。
ターゲットの考え方
目的変数、教師データなど様々な呼び方があるが、本記事ではターゲットという呼び方で統一する。株価予測におけるターゲットとは株価そのものの値ではなく、リターンである。
株価自体の予測はNG
これは言うまでもないことであるが、念のため補足しておく。株価をはじめ時系列データは単位根過程であり、要するにランダムウォークである。単位根過程は非定常過程であり、すなわち時間依存する系列である。非定常過程を分析に掛けた場合には見せ掛けの相関など諸所の問題が発生するが、そもそも時間依存するのであれば限られた期間のデータを用いて予測モデルを作ることに意味がないことは明白であろう。この辺りは参考サイトに詳しく論じられているので是非とも参考にすべきである。
リターン=階差系列を使うとどうか
そこで実際の分析では階差系列を用いる。単位根過程の階差系列は弱定常過程となり、これであれば機械学習で扱える。実際には単純な階差系列ではなく一期前からの変化率を使う。これがリターンである。リターンには単純な変化率ではなく、上昇下落の対称性の観点から対数変化率のほうが望ましいという説もある。階差系列には情報の喪失等の議論の余地は残るが、後述するマーケット要因を控除する理由により、リターンを使用すべきである。この点について市場構造を観察しながら詳しく見ていこう。
マーケットベータ
株価を論じる上で、マーケットベータの考え方は必須である。マーケットベータとは以下のように個別銘柄のリターン$ R_i $とマーケットインデックスのリターン$ R_M $との線形回帰のベータ値である。厳密にはリスクフリーレートを考慮する必要があるが、ここでは簡単のため省略した。マーケットベータの最も有名な提唱者はウィリアム・シャープである。この単純な線形回帰式で、なんと1990年にノーベル経済学賞を受賞している。マーケットにおいて、この式はそれほど重要な式なのである。
R_i=\alpha _i + \beta _i R_M + \epsilon _i \\
E[R_i] = E[\alpha _i] + \beta _i (E[R_M])
シャープの提唱したCAPMにおいて、上記の$ E[\alpha_i] $は0である。すなわち個別銘柄による超過収益の期待値は0であり、この仮定の下では個別銘柄の株価予測の問題とはベータの数値計算とマーケットの方向予測の問題でしかない。すなわち個別銘柄による予測モデルは全く意味をなさなくなる。
では本当にそうなのか。そんなことはない。様々な要因で超過収益は存在する。$ E[\alpha_i] $は期待レジデュアルリターンと呼ばれる項であり、またの名を「アルファ」という。
ここまでの説明で理解いただけたと思うが、個別銘柄の株価予測の問題は上記のアルファを予測する問題であり、マーケットの寄与分を控除して考える必要がある。アルファを予測した上で、マーケットの方向予測に別モデルを構築してマーケットリターンも享受しにいくか、もしくはインデックスショートなどでマーケットリスクをヘッジするのが妥当な考え方である。
線形回帰の残差分をターゲットとする考え方はEDAの一種である。しかしデータを与える以前に個別にタイムシリーズでの集計が必要であることから、単純にマーケットのリターンを特徴量の1つとして放り込んだとしても機械学習モデルがこの概念を作り出す可能性は低いだろう。まさしくドメイン知識を前提としたEDAなのである。
データを観察する
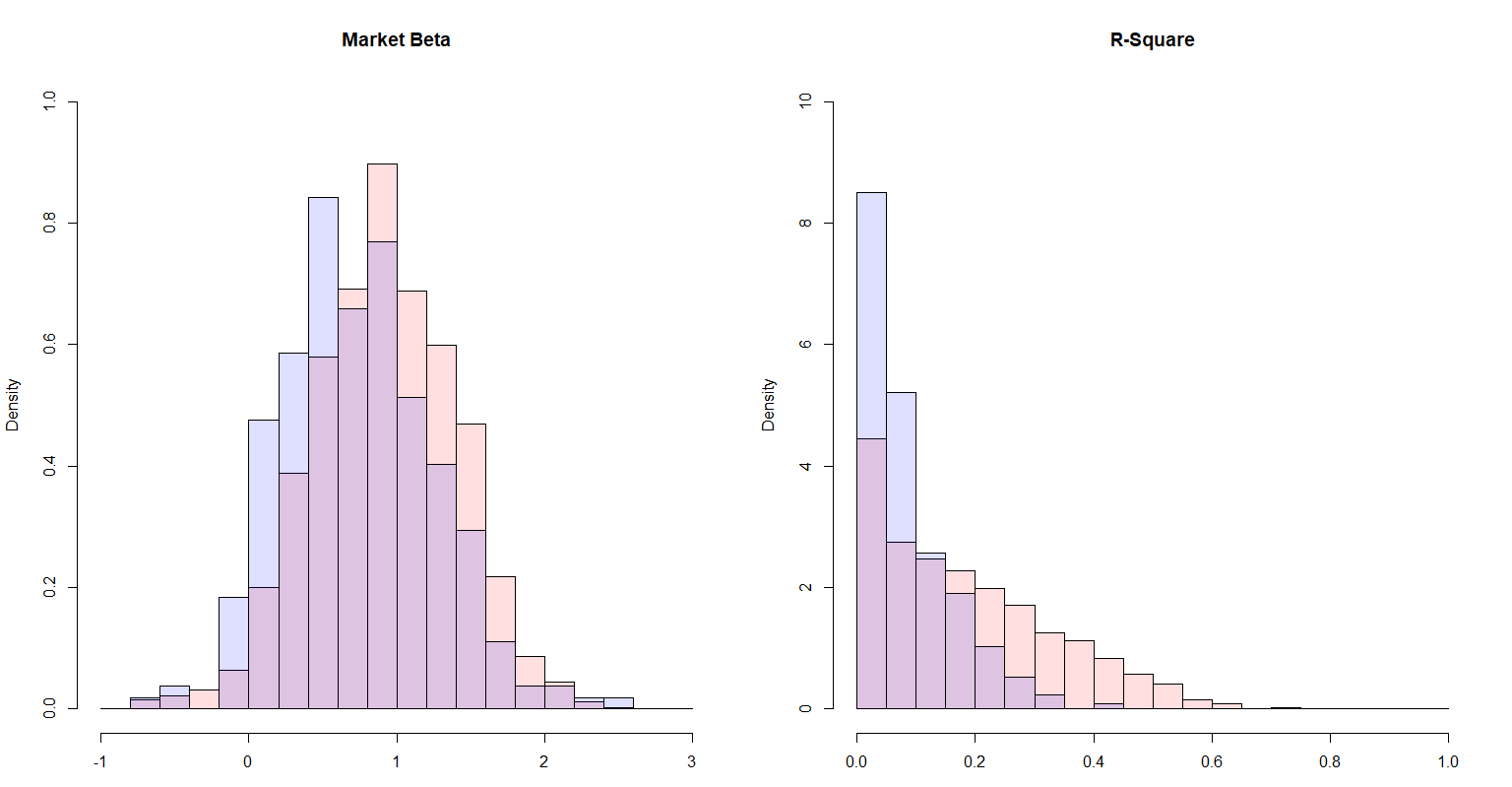
ではここでベータの分布を見てみよう。下左図は東証1部(赤)およびマザーズ市場(青)における、各銘柄のベータ値のヒストグラムである。集計した銘柄数は東証1部が2156銘柄、マザーズ市場が273銘柄である。マーケットインデックスは、それぞれTOPIX指数、マザーズ指数であり、各構成銘柄の時価総額加重平均として算出される。東証1部銘柄は概ねベータ1を中心とした正規分布となっている。一方でマザーズ銘柄は、一般的なハイリスク=高ベータの印象とは反してベータ値は低めとなっている。これはインデックスとの低相関に起因するものであり、相関係数の二乗である決定係数も同時に観察した(下右図)。この図から東証1部銘柄に対してマザーズ銘柄のマーケットインデックスによる説明力はやや希薄であることが確認できる。
マーケットリターンの説明力は、東証1部の銘柄において高いものは5割を超えるものがある。一方でマザーズの銘柄ではせいぜい3割以下であり、その影響は幾分軽微となる。このように株式銘柄は時価総額や上場している市場によって大きく挙動が異なるため、適切なユニバース選択を行うことが必要となる。ユニバースの選択も勘所が要求されるハイパーパラメータの1つと考えることができよう。
なおこれらのデータ収集~可視化のコードは割愛させていただく。このようなデータ集計にプログラミングテクニックは不要であり、また筆者は披露できるほどのコーディング能力は持ち合わせていない。
さらにリターンを細分化する
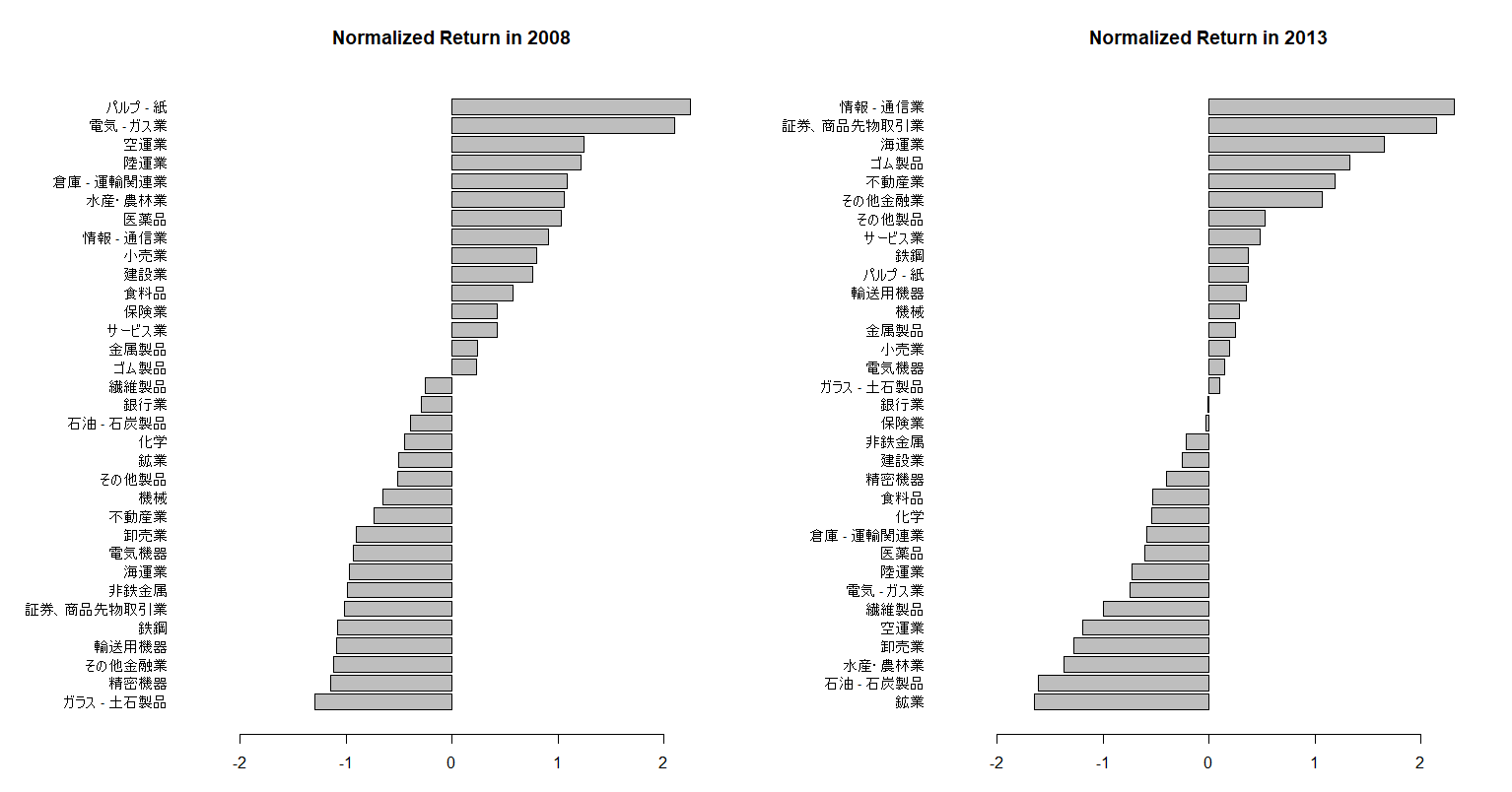
マーケットの構造をもう少しだけ深く覗いてみよう。株式の銘柄はその業務分野によっていくつかの業種に区分されている。最もよく使われている区分が東証33業種である。株式市場では、景気の拡大、成熟、後退、停滞というサイクルを通じて、その時々にアウトパフォームする業種が異なる。これをセクターローテーションと呼ぶ。下図は、各期間における各業種の騰落率を並べたものである。
当然ながら各銘柄のリターンは、マーケットによる寄与分のみならず、セクターローテーションからも多大な影響を受ける。このようにマーケット分を控除するだけでなく、セクターなどその他の要因まで切り分けた後に残る銘柄固有のリターンをスペシフィックリターンと呼ぶ。一般的に日本市場ではスペシフィックリターンが反発する性質を備えると言われている(スペシフィックリターンリバーサル)。
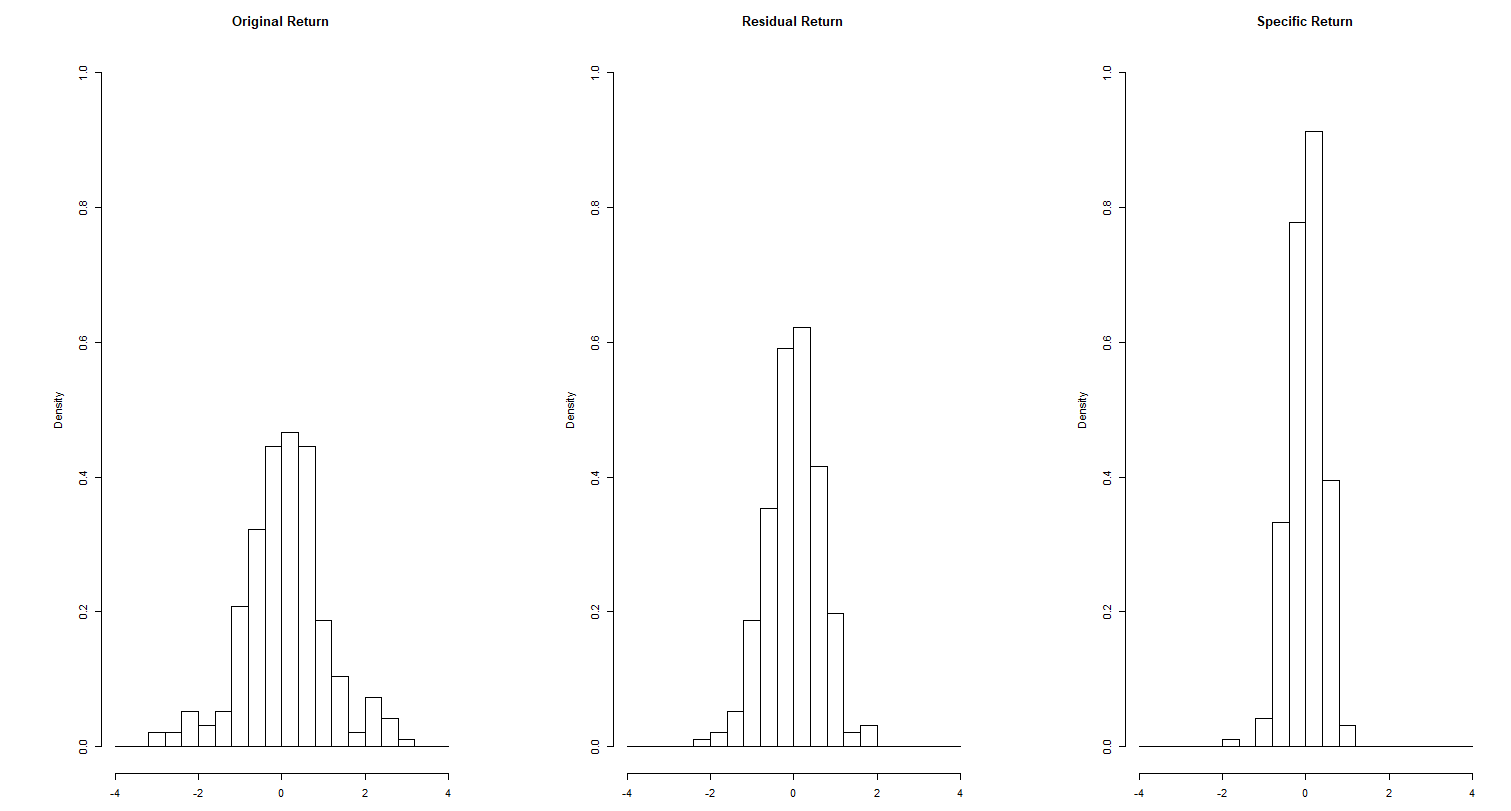
一例として、7203トヨタ自動車の日次リターン、レジデュアルリターン、スペシフィックリターンの分布を下図に示す。このような措置を講じるとターゲットの分散値を低減することができる。ターゲットの分散値を低減することは、検証の過程において種々のバイアスを避ける上で必須なのである。また、スペシフィックリターンは銘柄間のリターン相関を著しく低減できることから、実運用上においても多大な恩恵を受けることができる。
おわりに
本記事で説明したとおり、株価予測の問題はドメイン知識のない状態でとりあえずデータを放り込んで分析してもうまくいかない。仮に良い結果が得られたとしてもそのモデルには信憑性は存在せず、実際に運用したところですぐに中断に至ってしまうだろう。
上記のような勘所に触れた書籍は少ない。筆者はこれまでに数少ない情報を頼りに、独自で研究を行ってきた。本記事を読んだ後、もしも興味を湧いたのであればぜひ筆者のブログやnote、ツイッターも参照して頂きたい。