Akashic Engine で擬似3D

Akashic Advent Calendar 2019 十一日目の記事です。

Akashic Engine は2D専用ゲームエンジンです。コンソール機で言えばスーパーファミコンやメガドライブの世代とも言えますが、そんな時代にも擬似的な3D（奥行きのある表現）のゲームがありました。この記事では、 Akashic Engine で擬似的な3D表現を試みます。

ゴールの確認

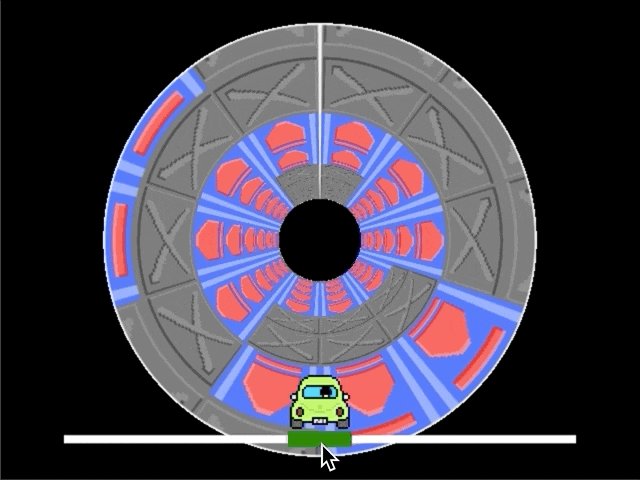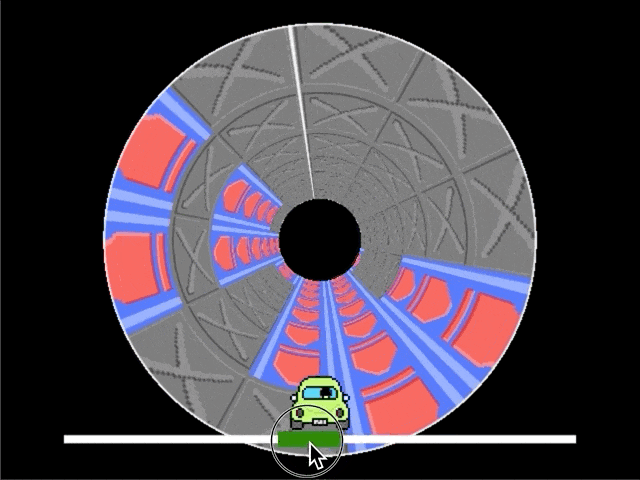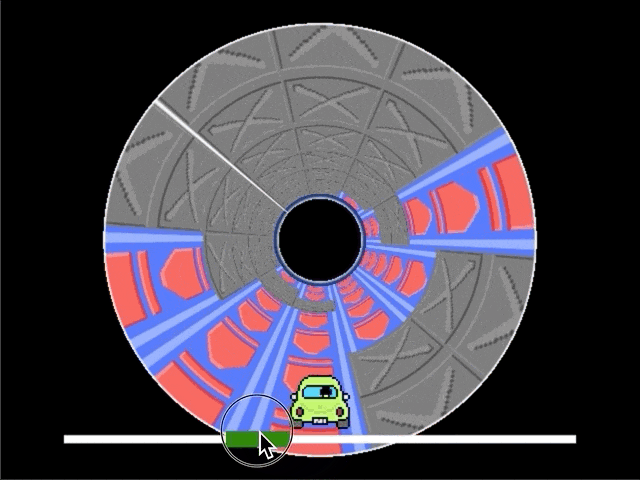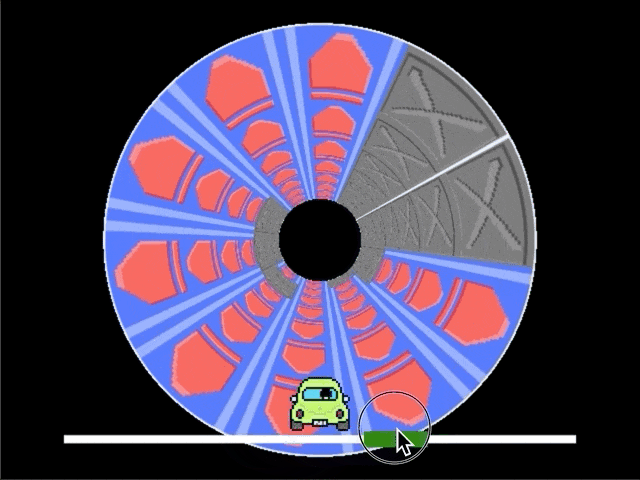
最初に完成形を確認しましょう。筒状の空間を進んでいくイメージです。

実装

実装は次の２段階で進めます。

1. 縦スクロールするフィールドの実装。
2. フィールドを筒状にレンダリングするシェーダの実装。

縦スクロールするフィールドの実装

フィールド用の画像（タイルチップ）を３つ使用します。

• ０番
• １番
• ２番

マップデータは単純な配列で、画像の番号の並びになっています。

const map = [
	// 1  2  3  4  5  6  7  8  9
	2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
	2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
	2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
	2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
	0, 0, 1, 1, 1, 1, 1, 1, 0, 0,
	0, 0, 0, 1, 1, 1, 1, 0, 0, 0,
	0, 0, 0, 0, 1, 1, 0, 0, 0, 0,
	0, 0, 1, 1, 1, 1, 0, 0, 0, 0,
	0, 0, 1, 1, 1, 1, 1, 0, 0, 0,
	// 省略
];

フィールドを描画する時、タイルチップを１つ１つ g.Sprite にする方法もありますが、フィールドを描画する専用の g.E 派生クラスを実装した方がシンプルで実行効率も良さそうです。フィールドを描画するクラス Road は次の通りです。

interface RoadParameterObject extends g.EParameterObject {
	posY: number;
	map: number[];
	mapWidth: number;
	surfaces: g.Surface[];
}

/**
 * タイルマップ描画役。
 */
class Road extends g.E {
	/** スクロール位置 */
	posY: number;

	/** マップデータ */
	map: number[];

	/** マップの横のタイル数 */
	mapWidth: number;

	/** マップの縦のタイル数 */
	mapHeight: number;

	/** タイル画像 */
	surfaces: g.Surface[];

	constructor(param: RoadParameterObject) {
		super(param);

		this.posY = param.posY;
		this.map = param.map;
		this.mapWidth = param.mapWidth;
		this.mapHeight = param.map.length / param.mapWidth;
		this.surfaces = param.surfaces;
	}

	renderSelf(renderer: g.Renderer, camera?: g.Camera): boolean {
		const tileWidth = this.width / this.mapWidth;
		const tileHeight = tileWidth; // ここではタイルを常に正方形に描画する。

		let mapPosY = (this.posY / tileHeight) % this.mapHeight;
		if (mapPosY < 0) {
			mapPosY += this.mapHeight;
		}

		let yi = mapPosY | 0;
		const yf = mapPosY - yi;

		renderer.save();

		for (let y = this.height - tileHeight * yf; y > -tileHeight; y -= tileHeight) {
			for (let i = 0; i < this.mapWidth; i++) {
				const tileId = this.map[(yi * this.mapWidth + i) % this.map.length];
				const surface = this.surfaces[tileId];

				renderer.setTransform([
					tileWidth / surface.width, 0,
					0, tileHeight / surface.height,
					i * tileWidth, y
				]);

				renderer.drawImage(
					surface,
					0, 0,
					surface.width, surface.height,
					0, 0
				);
			}

			yi -= 1;
			if (yi < 0) {
				yi += this.mapHeight;
			}
		}

		renderer.restore();

		return true;
	}
}

Road は width の幅に mapWidth 個のタイルチップを並べます。タイルチップの横幅は width / mapWidth になり、縦幅と横幅は同じ大きさになります。タイルチップ画像のサイズは同じにする必要はなく、適宜拡大縮小されます。

Road の実行結果です( Road#posY を更新しています）。

フィールドを筒状にレンダリングするシェーダの実装

次にシェーダで筒状にします。 Road のレンダリング結果を g.Pane でキャッシュし、そのキャッシュされた画像にシェーダを適用します。

g.Secne/g.E のツリーはこのような構造になります。

scene
└── pane1 (pane2 にシェーダを適用してレンダリングする)
    └── pane2 (road のレンダリング結果を保持する)
        └── road

ではシェーダを実装しましょう。タイルチップによるフィールドを筒状に変形する、とはどのようなシェーダになるのでしょうか。

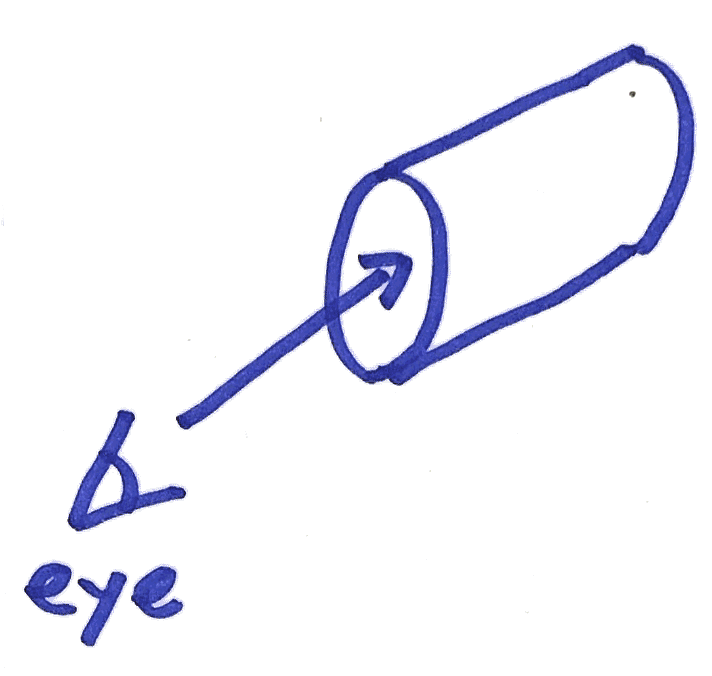
筒状にする、ということは、紙を丸めて覗きこむことです。

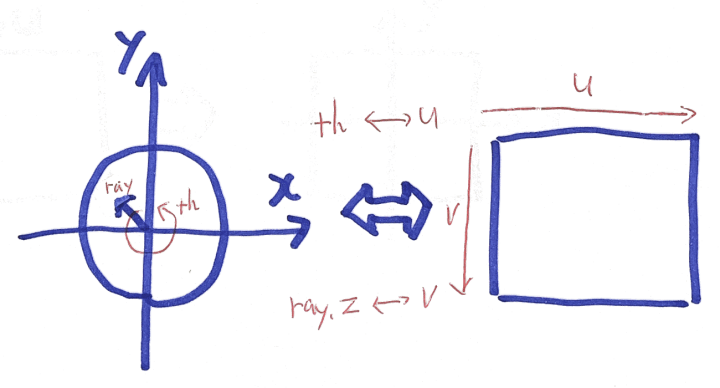
これをシェーダで扱えるように、視点と筒を適当な座標系に配置してみます。

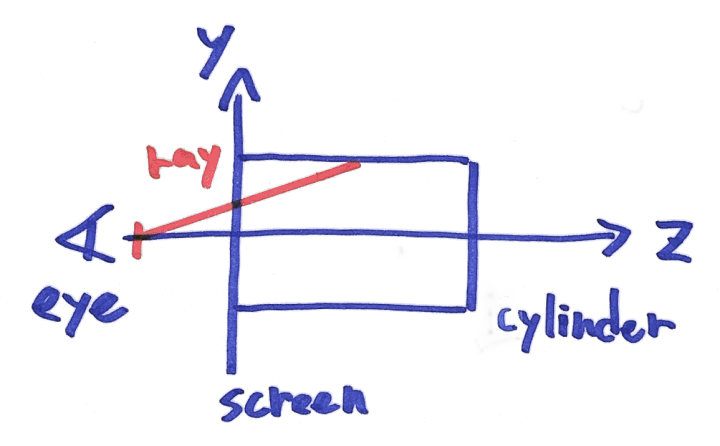
これで「視点から円筒の中はどのように見えるのか」を考える準備ができました。

フラグメントシェーダは、ものすごく大雑把に言えば「このピクセルの色は何色か」について答える関数です。図中の赤い線 ray はこれに答えるための補助線です。ray は eye からスクリーン(XY平面)上の１点（フラグメントシェーダが色を決めるピクセルの位置） を通して伸びていき、円筒に達します。ray がヒットした座標から円筒の内側に貼り付けられた画像（ここでは Road のレンダリング結果）のどの画素にあたるかが定まります。それがシェーダの返り値となります。

シェーダは次のようになります。

#version 100

precision mediump float;

#define PI 3.1415926535

// テクスチャ。
uniform sampler2D uSampler;

// UV座標。
varying vec2 vTexCoord;

// シェーダが適用される画像の横幅。
uniform float image_width;

// シェーダが適用される画像の縦幅。
uniform float image_height;

// 円筒のZ回転角。
uniform float rotZ;

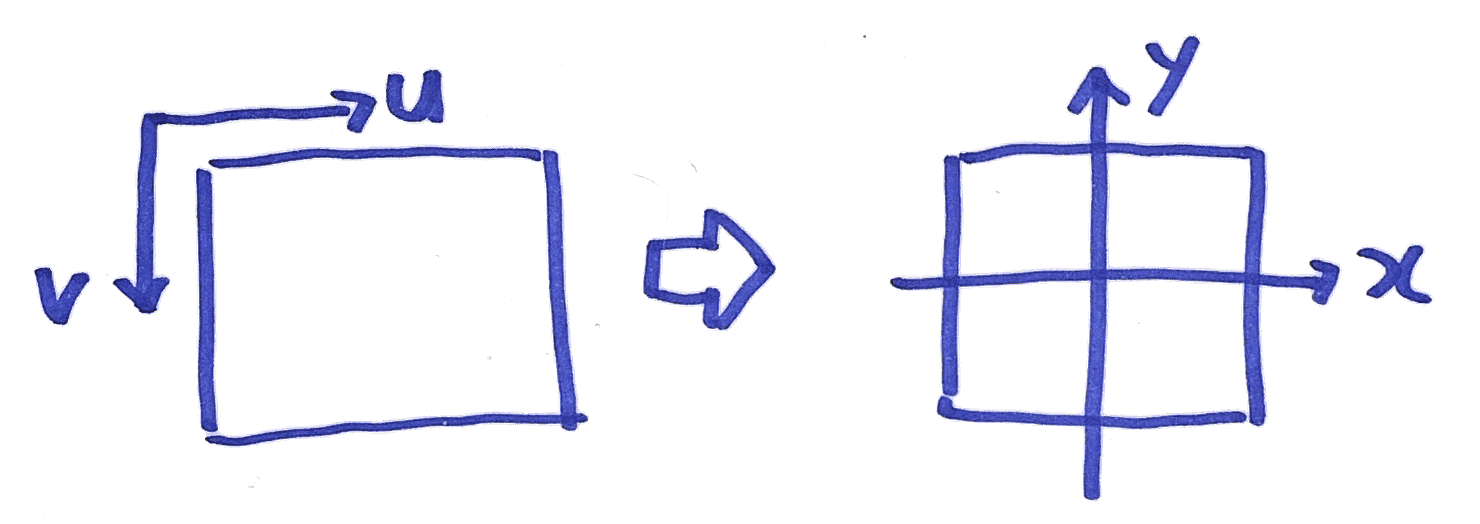
// 矩形上のUV座標を３次元座標系に変換する。
vec2 toScreenSpaceXY(vec2 uv) {
    vec2 xy = vec2(uv.x, 1. - uv.y) * 2. - vec2(1., 1.);

    if (image_width >= image_height)
        xy.x *= image_width / image_height;
    else
        xy.y *= image_height / image_width;

    return xy;
}

// 回転行列を作る。
mat2 rotationMatrix(float angle) {
    float c = cos(angle);
    float s = sin(angle);
    return mat2(c, -s, +s, c);
}

void main () {
    vec2 p = toScreenSpaceXY(vTexCoord);

    // シリンダー半径。
    float cr = 0.9;

    // シリンダーの円周の長さ。
    float C = 2. * PI * cr;

    // シリンダーの高さ（Z方向の長さ）。
    float H = C * (image_height / image_width);

    // カメラ（視点）の位置。
    vec3 c = vec3(.0, .0, -1.);

    // レイ。
    vec3 ray;

    // レイの方向(XY成分)
    ray.xy = p - c.xy;

    // レイのXY成分の長さ。
    float l = length(ray.xy);

    // 円筒の外は黒くする。
    if (l > cr) {
        gl_FragColor = vec4(0., 0., 0., 1.);
        return;
    }

    // ray と 円筒の交差点のZ座標。
    ray.z = (1. - cr / l) * c.z;

    // 円筒の先端より先にレイが伸びている時、黒くする。
    if (ray.z > H) {
        gl_FragColor = vec4(0., 0., 0., 1.);
        return;
    }

    // 円筒を回転させるため、レイの方向(XY成分)を逆回転させる。
    ray.xy = rotationMatrix(-rotZ) * ray.xy;

    // 0時の方向から反時計回りになるようにする。
    float th = atan(ray.x, -ray.y);
    float u = (th + PI) / 2. / PI;
    float v = ray.z / H;

    gl_FragColor = texture2D(uSampler, vec2(u, v));
}

肝心な箇所をかいつまんで説明します。

最初に vTexCoord (テクスチャのUV座標)を toCenterizedUV() でレイの計算のための XY 座標に変換します。

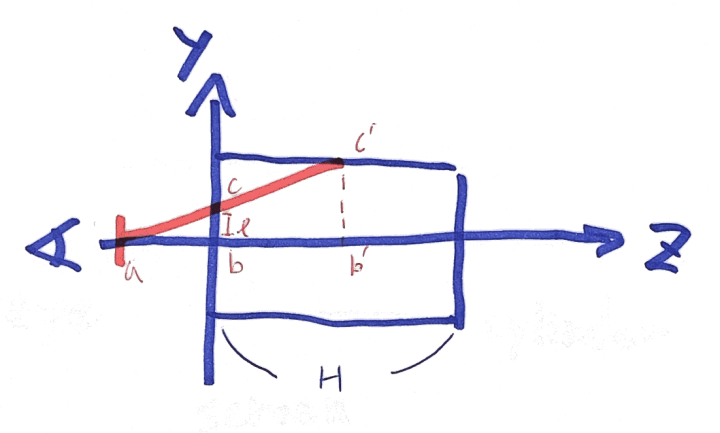
レイと円筒の交差点のZ座標を求めているのは次の行になります。

    ray.z = (1. - cr / l) * c.z;

△abcと△ab'c'が相似であることを利用しています。

最後に ray から uv を求めています。

    float th = atan(ray.x, -ray.y);
    float u = (th + PI) / 2. / PI;
    float v = ray.z / H;

レイの向き（Z軸周りの角度th）を u に、 ray.z を v に変換しています。

駆け足になりましたが、シェーダの説明は以上になります。デモはGitHubから入手できます。

課題

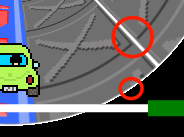
筒の一部に意図しない白い線が現れています。

おそらく、Road のレンダリング結果が大きなテクスチャの一部として保持されていて、レンダリング結果に隣接する白い画素がにじみ出ているのだと思います。 Road のレンダリング結果を保持する g.Pane に手を加えて、キャッシュされた画像の外周ににじみを目立たなくする色を塗っておくといった工夫で回避できると思います。

最後に

この記事では、シェーダによって円柱内部を進むような3D表現を実装しました。3Dという言葉から思い浮かぶ自由度からはずいぶん遠いところにあるものですが、参考になればと思います。