ABテストの期間を見積もる際に、必要なサンプルサイズを求める必要があるが、Web上に公開されているツールをどの程度信用してよいかわからないため、論文を調査し理解を深めた。
必要なサンプルサイズを計算する式の導出をメモすることがメインだが、ついでにABテストに必要そうな統計の知識をまとめておきます。
ツールも作っておきました↓
AAテストについてはこちら。
基本用語
基本的な用語とこの記事で使う記法を定義しておきます。
-
母集団: 知りたい集団全体
- 母平均$\mu$: 母集団におけるある値の平均のこと
- 母分散$\sigma^2$: 母集団におけるある値の分散のこと
- 母比率$p$: 母集団において、ある事象が起こる確率のこと
-
標本: サンプリングされた集団
- 標本平均$\bar x$: 標本集団におけるある値の平均のこと
- 標本分散$S^2$: 標本集団におけるある値の分散のこと $S^2=\frac{1}{n}\sum_{i=1}^n(x_i-\bar x)^2$
- 不偏分散$s^2$: $s^2=\frac{n}{n-1}S^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar x)^2$
- 標本比率$\bar p$: 標本集団で計算した、ある事象が起きる確率のこと
- 帰無仮説$H_0$: 棄却したい仮説
- 対立仮説$H_1$: 帰無仮説が棄却されたときに採択される仮説
- 有意水準$\alpha$: 帰無仮説を棄却する基準となる確率
- 検出力$1-\beta$: 帰無仮説が正しくないときに、正しく棄却する確率
- P値: 帰無仮説のもとで検定統計量がその値orそれより極端な値になる確率のこと。有意水準以下なら帰無仮説を棄却する
- 中心極限定理: 平均$\mu$、分散$\sigma^2$をもつ任意の分布からの無作為標本の標本平均の分布は$n$が十分大きいとき$N(\mu, \sigma^2/n)$に従う
- サンプルサイズが十分大きい: $n\ge 30$が目安らしい
- 対応があるデータ: 2つのデータが同一の標本から得られた場合
- 対応がないデータ: 2つのデータが別々の標本から得られた場合
検定
ABテスト実施後、「本当に効果があったと言えるのか？」を統計的に有意と言うためには、検定をする必要があります。
検定の流れ
- 仮説を立てる
- 帰無仮説$H_0: \bar x=\mu$
- 対立仮説（成り立ってほしい仮説を1つ設定する）
- $H_1: \bar x\ne \mu$（両側検定）
- $H_1: \bar x < \mu$（片側検定）
- $H_1: \bar x > \mu$（片側検定）
- 有意水準$\alpha$を設定
- 0.05がよく使われる
- 検定統計量を計算し、棄却される領域に入るかどうか確認する
- 棄却領域内 → 対立仮説が正しいと判断
- 棄却領域外 → 何も言えない
統計量が正規分布に従う場合のイメージ図（$\alpha=0.05$）
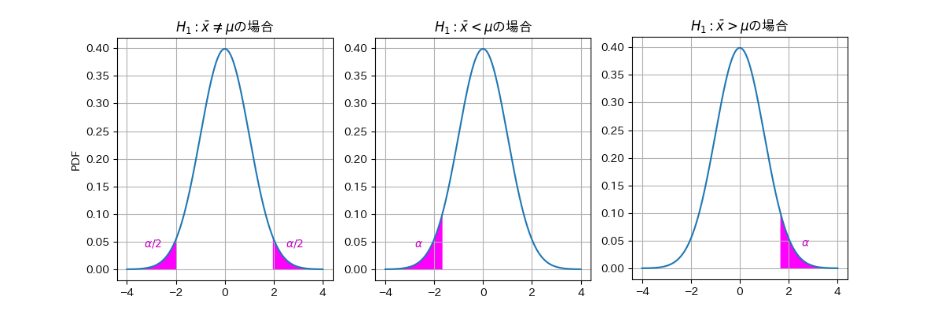
色の塗られた領域の合計面積が$\alpha$で、対応する横軸の領域が棄却領域です。
計算した統計量が、棄却領域内に入る場合、極めて稀な事象が起きたことを意味するため、帰無仮説を棄却して対立仮説を採択するわけです。
1標本検定
まずは、1つの群の推定量を検定する基礎的な検定の話です。
基本的にABテストでは2群が登場するので直接の関係はありません。
母平均の検定
使用条件
- 母集団が正規分布に従う OR サンプルサイズが十分大きい
統計量の従う分布
検定統計量$\displaystyle
t=\frac{\bar x-\mu}{\sqrt{s^2/n}}
$は自由度$(n-1)$のt分布に従う。
この$t$の値が棄却領域に入るかどうかを確認します。
設定した有意水準に対応する横軸の値はt分布表で調べます。
補足
サンプルサイズが十分大きい場合、t分布は正規分布で近似できます。
母比率の検定
使用条件
- サンプルサイズが十分大きい
統計量の従う分布
検定統計量$\displaystyle z=\frac{\bar p-p}{\sqrt{p(1-p)/n}}$は標準正規分布に従う。
この$z$の値が棄却領域に入るかどうかを確認します。
設定した有意水準に対応する横軸の値は標準正規分布表で調べます。
補足
ベルヌーイ分布の和の分布は二項分布に従い、二項分布の平均が$np$、分散が$np(1-p)$であることから導かれます。
2標本検定
次に、2つの群に関する検定です。
ABテストのように、A群とB群を比較するような状況で使います。
各群に関する値を参照するときは、群の名前を添字として付与して表記することにします:
- $\bar x_A$: A群の標本平均
- $s_A$: A群の不偏分散
- $n_A$: A群のサンプルサイズ
- $\bar p_A$: A群の標本比率
母平均の差の検定
2群の平均値を比較したい場合の検定です。
使える条件によって名前がついているので
- スチューデントのt検定
- ウェルチのt検定
の2つを紹介しますが、この2つの場合、より条件の緩いウェルチのt検定を使っておけばいいと思います。
スチューデントのt検定
使用条件
- 2つの母集団が正規分布に従う OR 各群のサンプルサイズが十分大きい
- 2群のデータは対応していない
- 2群の母分散が等しい
統計量の従う分布
検定統計量$\displaystyle
t=\frac{\bar x_A-\bar x_B}{\sqrt{s^2(1/n_A+1/n_B)}}
$は自由度$\nu=n_A+n_B-2$のt分布に従う。
ただし、$\displaystyle s^2=\frac{(n_A-1)s_A^2+(n_B-1) s_B^2}{n_A+n_B-2}$はプール（重み付き平均）した不偏分散です。
この$t$の値が棄却領域に入るかどうかを確認します。
ウェルチのt検定
使用条件
- 2つの母集団が正規分布に従う OR 各群のサンプルサイズが十分大きい
- 2群のデータは対応していない
- 2群の母分散が等しいとは限らない
統計量の従う分布
検定統計量$\displaystyle
t=\frac{\bar x_A-\bar x_B}{\sqrt{s_A^2/n_A+s_B^2/n_B}}
$は自由度$\displaystyle \nu\approx\frac{({s_A^2}/{n_A}+{s_B^2}/{n_2})^2}{{s_A^4}/{n_A^2(n_A-1)}+{s_B^4}/{n_B^2(n_B-1)}}$のt分布に従う。
この$t$の値が棄却領域に入るかどうかを確認します。
母比率の差の検定
比率（クリック率やコンバージョン率など）に有意な差があったかなどを確認するときに使います。
使用条件
- 各群のサンプルサイズが十分大きい
- 2群のデータは対応していない
統計量の従う分布
検定統計量$\displaystyle
z=\frac{\bar p_A-\bar p_B}{\sqrt{\bar p(1-\bar p)(1/n_A+1/n_B)}}
$は標準正規分布に従う。
ただし、$\displaystyle \bar p=\frac{n_A\bar p_A+n_B\bar p_B}{n_A+n_B}$はプール（重み付き平均）した標本比率です。
この$z$の値が棄却領域に入るかどうかを確認します。
設定した有意水準に対応する横軸の値は標準正規分布表で調べます。
ボンフェローニ補正
多重検定（検定を重ねる）を行うと、偶然有意水準を満たしてしまうような結果が出やすくなります。
たとえば3群以上の差を相互に検定するケースがこれにあたります。
このようなエラーの増大を防ぐための補正法にボンフェローニ補正というものがあります。
満たしたい有意水準を$\alpha$としたとき、行う検定の数を$N$とすると、各検定の有意水準を$\alpha/N$にして実施するというシンプルな方法です。
なお、ボンフェローニ補正はシンプルですが、かなり保守的な手法で、検定を重ねすぎると棄却しにくくなるため、たくさん重ねる場合は他の手法を検討したほうがいいです。
必要なサンプルサイズの見積もり
いよいよ本題です。
ABテストの計画を立てる際に、どれくらいの期間実施するのかを計画する必要が出てきます。
検定したい設定を決めると、必要なサンプルサイズを見積もることができます。
具体的には、
- 有意水準: $\alpha$
- 検出力: $1-\beta$
- 検出したい差: $\mu_A-\mu_B$
- 分散: $\sigma^2$
を定めた時、「どれだけのサンプルサイズが必要なのか？」を計算します。
必要なサンプルサイズを、1日で獲得できるサンプル数で割ることで必要な日数を求めることができます。
結論
先に結論を書きます。
A群B群の標本数は等しいと仮定します。
母平均の差の検定の場合、2群それぞれに必要なサンプル数は
- 両側検定のとき: $$n=\frac{2\sigma^2(z_{1-\alpha/2}+z_{1-\beta})^2}{(\mu_A-\mu_B)^2}$$
- 片側検定のとき: $$n=\frac{2\sigma^2(z_{1-\alpha}+z_{1-\beta})^2}{(\mu_A-\mu_B)^2}$$
で概算されます。$\sigma^2$が未知の場合$s^2=(s_A^2+s_B^2)/2$で代替する。
母比率の差の検定の場合、2群それぞれに必要なサンプル数は
- 両側検定のとき: $$n=\frac{2\bar p(1-\bar p)(z_{1-\alpha/2}+z_{1-\beta})^2}{(\bar p_A-\bar p_B)^2}$$
- 片側検定のとき: $$n=\frac{2\bar p(1-\bar p)(z_{1-\alpha}+z_{1-\beta})^2}{(\bar p_A-\bar p_B)^2}$$
で概算されます。ただし、$\bar p=(\bar p_A+\bar p_B)/2$。
ここで、$z_k$は標準正規分布の累積密度が$k$であるときの$x$軸の値です。
たとえば、両側検定で有意水準$\alpha=0.05$、検出力$1-\beta=0.8$としたとき、$z_{1-\alpha/2}\approx 1.96,z_{1-\beta}\approx 0.84$で、
$$
n=\frac{2\sigma^2(1.96+0.84)^2}{(\mu_A-\mu_B)^2}
=\frac{15.68 \sigma^2}{(\mu_A-\mu_B)^2}
\left(\approx\frac{16 \sigma^2}{(\mu_A-\mu_B)^2}\right)
$$
のサンプルサイズが各群に必要です。
最後に書いた係数16の式は、簡単に計算できるルールとして論文等で紹介されていました。
導出
このサンプルサイズの式はいろいろなところに載っているけど、なかなか導出が載っていなかったので苦労しました。導出に近い論文を見つけたので、自分なりに余白を埋めつつ説明します。
両側検定
- 帰無仮説$H_0: \mu_A=\mu_B$
- 対立仮説$H_1: \mu_A\ne\mu_B$
を考えます。
$H_0$による分布を$f(x)$、$H_1$による分布を$f(x-x_0)$とします。
（$x_0$だけずれている、すなわち差があるということです。この$x_0$は後に具体化させます。）
ここで、$f(x)$は原点対称$f(x)=f(-x)$を満たす分布とします。（標準正規分布、t分布など）
以下がイメージ図です。
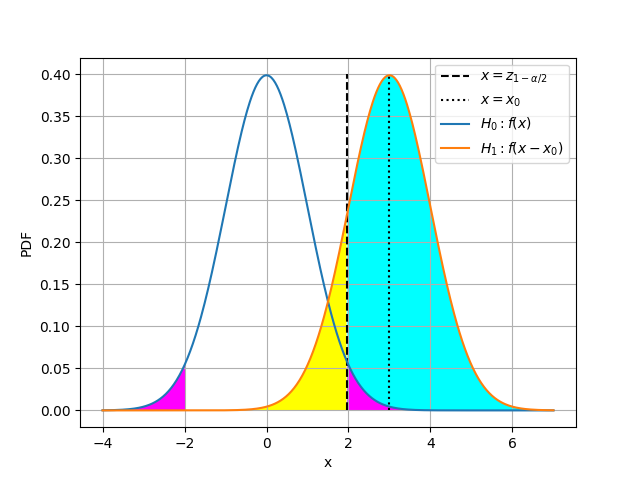
この図で、黄色部分の面積が$\beta$、シアン部分の面積が検出力$1-\beta$、マゼンタ部分の面積が有意水準$\alpha$となります。
$z_k$の定義は、累積密度（面積）が$k$となるときの$x$の値であり、
$$
k = \int_{-\infty}^{z_k}f(x)dx
$$を満たす値です。
分布の対称性と、全区間の積分値が1であることから$z_k=-z_{1-k}$という性質を持ちます。
ここで黄色部分の面積を式で表現すると、
$$
\int_{-\infty}^{z_{1-\alpha/2}}f(x-x_0)dx
=\int_{-\infty}^{z_{1-\alpha/2}-x_0}f(x)dx
$$と表現できますが、黄色部分の面積は$\beta$であるため、$z_{1-\alpha/2}-x_0=z_{\beta}$が成り立ちます。
ここで、$z_{\beta}=-z_{1-\beta}$なので、
$$x_0=z_{1-\alpha/2}+z_{1-\beta}$$が成り立ちます。
ここで$x_0$を具体化していきます。
平均値の差の検定方法である「スチューデントのt検定」では、
統計量
$$
t=\frac{\bar{x}_A-\bar{x}_B}{\sqrt{s^2(1/n_A+1/n_B)}}
$$が自由度$n_A+n_B-2$のt分布に従うことを用いて検定を行いました。
したがって、$f(x)$はt分布、$x_0=t$で考えることになります。
x_0
=\frac{\bar{x}_A-\bar{x}_B}{\sqrt{s^2(1/n_A+1/n_B)}}
=z_{1-\alpha/2}+z_{1-\beta}
2群のサンプルサイズが等しい$n=n_A=n_B$と仮定して、この式を$n$について解きたいですが、分布の自由度に$n$が現れており$z_*$が$n$に依存するため解けません。
t分布は自由度が十分に大きいとき、標準正規分布に近づくので、近似として正規分布を使うことにすると、$n$について解くことで、
$$
n=\frac{2s^2(z_{1-\alpha/2}+z_{1-\beta})^2}{(\bar{x}_A-\bar{x}_B)^2}
$$を得ます。
（ちなみに、サンプルサイズが等しいとき、$s^2=(s_A^2+s_B^2)/2$であるため、ウェルチのt検定の式からでも同じ結果を導けます。）
母比率の場合は、サンプル数が十分大きい場合、統計量
$$
z=\frac{\bar p_A-\bar p_B}{\sqrt{\bar p(1-\bar p)(1/n_A+1/n_B)}}
$$が標準正規分布に従うため、同じように$n=n_A=n_B$について解くことでサンプルサイズの式を得ます。
参考文献
-
Biostatistics A Methodology For the Health Sciences
- 基本的な統計の知識から説明した約900ページのPDFです
- 母平均の差の検定のサンプルサイズ見積もりの式とフロー図が書かれています
- 分散をデータから見積もった場合には、さらに定数（1～4程度）を足すと書かれていました（あくまで概算ということでいいと思います）
-
All about Sample-Size Calculations for A/B Testing: Novel Extensions & Practical Guide
- 母平均/母比率の差の検定のサンプルサイズ見積もりの式が書かれています
-
統計Web
- 基本的な統計の知識を復習できました
-
比率の差の検定におけるサンプルサイズの計算
- このサイトのおかげで下記論文にたどり着けました
-
Sample Size Calculation for Comparing Proportions
- 行間を埋める必要はありましたが、サンプルサイズの式の導出が書かれていました
おまけ: 自作ツールの正しさの確認
-
Sample Size Calculator
- Adobeの計算サイトとほぼ値が一致することを確認
-
2標本検定
- 母平均の差の検定
ツールには以下を入力
from scipy.stats import ttest_ind x=[1,1,2,3,4,9] y=[2,3,1,2,3,5] ttest_ind(x, y, equal_var=False, alternative="two-sided") # -> Ttest_indResult(statistic=0.4938647983247951, pvalue=0.636571897759369)import numpy as np print(np.mean(x), np.mean(y)) # -> 3.3333333333333335 2.6666666666666665 print(np.var(x, ddof=1), np.var(y, ddof=1)) # -> 9.066666666666666 1.8666666666666667 print(len(x), len(y)) # -> 6 6 - 母比率の差の検定
from statsmodels.stats.proportion import proportions_ztest proportions_ztest([0.3*1000, 0.35*900], [1000, 900], alternative="two-sided") # -> (-2.3258351936480293, 0.0200273443634706)
- 母平均の差の検定