Keywords: Safe Screening, セーフスクリーニング, スクリーニング, 凸最適化, 最適性

Safe Screening

Safe Screeningとは, 機械学習の最適化計算において, 最適性に影響を与えない不要な制約や損失を消去し, 高速化をはかる手法である.

Safe Screeningの具体的な適用問題として, LASSOやSVMが挙げられる.
スパースモデルであるLASSOでは, 多くの係数 $w$ が0となるため, 事前に $w_i=0$ となるような特徴 $i$ を同定し除外することができれば, 除外されずに残った特徴のみで最適化を行えばよく, 学習の高速化につながる.
一方, SVMはヒンジ損失最小化学習として解釈されるが, 全サンプルのうち重要なサンプルは, ヒンジの角に集まるサポートベクトルのみである.
ヒンジの角におらず最適解で損失を発生させないサンプルは, 実際には学習には不要であり, あってもなくても変わらない.
そのようなサポートベクトルとはなりえないサンプルを除外することで, 学習の高速化を行える.

典型的なScreeningの手続き:
Step1. 最適解を含む小さな領域 (Bound) を現在の解から求める
Step2. 解がバウンド内にいる限り必ず成り立つ不要な制約や特徴, 損失を見つけて, 最適化問題から削除する

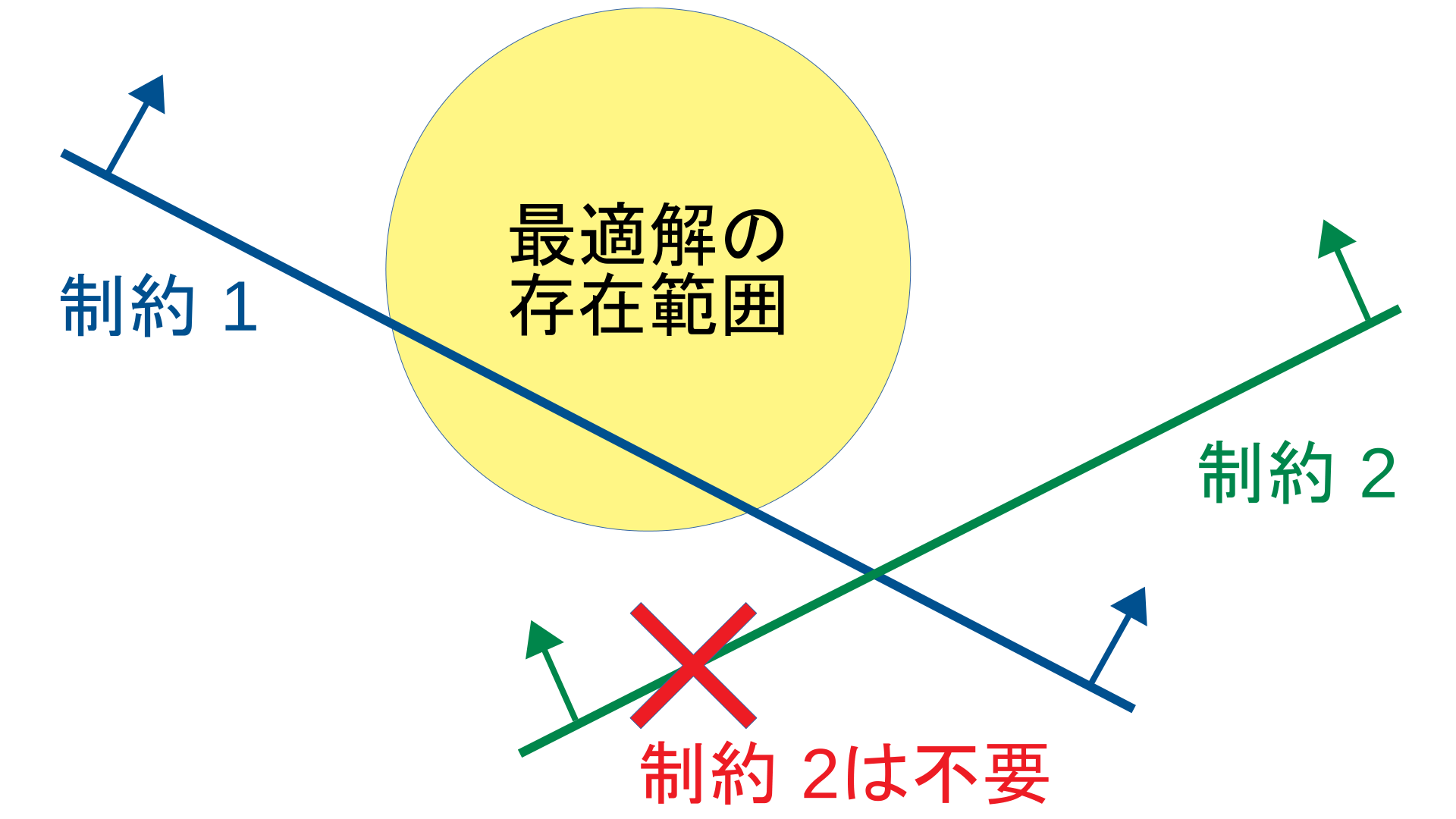
制約を例にあげると, Step1.で最適解の存在範囲を求められれば, 無効制約 (解に影響を与えない制約)となる制約を特定することができ, 最適化問題から削除することができる.

Bound

Screeningを行うには, まず最適解の存在範囲 $\cal B$ を求める必要がある.
この節では, 以下の最適化問題に関していくつかのBoundを示す.

$$
\tag{主問題}
\min_{w\in \mathbb{R}^d} P_\lambda(w):=\sum_{i=1}^N\ell(y_i, x_i, w)+\frac{\lambda}{2}\|w\|_2^2
$$

$\ell$: 凸な損失関数
$\lambda$: 正則化係数 (ハイパーパラメータ)

以下では, $w$に関して球状のバウンドを示していく.

Gradient Bound (GB)

任意の実行可能解 $w$ に対して, 最適解$w^\star$は次の超球内に存在する.
$$
\left\|w^\star -\left(w-\frac{1}{2\lambda}\nabla P _\lambda(w) \right) \right\|_2^2 \le \left\| \frac{1}{2\lambda} \nabla P _{\lambda}(w) \right\| _2^2 .
$$

$\nabla P_\lambda (w)$: 目的関数の勾配
半径に勾配の大きさを含むため, Gradient Boundという

証明
一般に凸最適化において, 次の定理が成り立つ (Convex Optimization4.2.3参照).
定理(凸最適化の最適性条件) 最小化問題$\displaystyle\min_{x\in\mathcal{F}}f({x})$において，実行可能領域$\mathcal{F}$および関数$f({x})$が凸であるとき, ${x}^\star$が最適解である必要十分条件は,
$$
\exists \nabla f({x}^\star)\in\partial f({x}^\star)\left[\nabla f({x}^\star)^\top ({x}^\star-{x})\le0,~\forall {x}\in\mathcal{F}\right],
$$
である. ただし$\partial f({x}^\star)$は${x}^\star$における劣勾配の集合を表す.
この定理を感覚的に理解するには, 以下の図を見るとよい.

最適解と実行可能解を結ぶベクトル$x-x^\star$と最適解における勾配降下方向$-\nabla f(x^\star)$のベクトルの内積は0以下になる.

この定理から, 任意の実行可能解$w$に関して,
$$
\tag{1}
\nabla P_{\lambda}({w}^\star)^\top ({w}^\star-{w}) \le 0
$$
が成り立つ.
損失関数$\ell(y_i, x_{i}, w)$の$w$における劣勾配を${\xi}_i(w)$とおけば,

$$
\tag{2}
\nabla P_{\lambda}(w)=\sum_{i}{\xi}_{i}(w)+\lambda {w}.
$$

損失関数$\ell(y_i, x_{i}, w)$の凸性 (凸関数の接線の値はその凸関数を超えない)から,
$$
\begin{split}
\ell(y_i, x_{i}, w^\star) &\ge \ell(y_i, x_{i}, w) + \xi_i(w)^\top (w^\star-w), \\
\ell(y_i, x_{i}, w) &\ge \ell(y_i, x_{i}, w^\star) + \xi_i(w^\star)^\top (w-w^\star),
\end{split}
$$

が, 任意の劣勾配において成り立つ. (劣勾配の定義でもある)
この2式を加えることで,

$$
\tag{3}
\xi_{i}(w^\star)^\top(w^\star-w)\ge \xi_{i}(w)^\top(w^\star-w).
$$

式(1), (2), (3)を組み合わせると,

$$
\begin{split}
( \sum_{i}\xi_{i}(w)+\lambda w^\star)^\top (w^\star-w) \le 0\\
\Leftrightarrow
(\nabla P_{\lambda}(w)-\lambda w+\lambda w^\star)^\top (w^\star-w) \le 0.
\end{split}
$$

これを平方完成すれば, GBが得られる.

Duality Gap Bound (DGB)

任意の主問題の実行可能解$w$と双対問題の実行可能解${\alpha}$に対して, 主問題の最適解$w^\star$は, 次の超球内に存在する.

$$
\left\|w^\star-w \right\|_2^2 \le \frac{2(P _{\lambda}(w)-D _{\lambda}({\alpha}))}{\lambda}.
$$

$D_\lambda(\alpha)$: 双対問題
半径に双対ギャップを含むためDuality Gap Boundという

双対性/双対問題に関しては, ラグランジュ双対問題について解説を参照.

証明
主問題の目的関数は, 凸な損失関数$\ell$と2乗ノルムの和であるため, $\lambda$-強凸関数である．

定義($m$-強凸関数) $f({x})-\frac{m}{2}\left\|{x}\right\|_2^2$が凸関数であるとき, $f({x})$は$m$-強凸関数であるという.

主問題の目的関数の強凸性(Strongly convex functions)から任意の$w,w^\star$について，次が成り立つ．

$$
P_{\lambda}(w)\ge P_{\lambda}(w^\star)+ \nabla P_{\lambda}(w^\star)^\top (w-w^\star)+\frac{\lambda}{2}\left\|w-w^\star\right\|_2^2.
$$

$w^\star$を主問題の最適解とすれば, 最適性条件の式(1)から, 右辺の第2項は0以
上$\nabla P_{\lambda}({w}^\star)^\top ({w}-{w}^\star) \ge 0$である.
また, 弱双対性から $P_{\lambda}(w^\star)\ge D_{\lambda}({\alpha})$．
これらの3つの不等式を組み合わせれば, DGBが得られる.

その他のバウンドやバウンド間の関係, 制約付き問題の取り扱いに関しては, Safe Triplet Screening for Distance Metric Learningを参照.
特に主問題に制約がある場合には, 最適解においてGBの半径が0に収束しない(勾配の大きさが残る)ため, 実用的には修正が必要となる.

Screening Rule

2クラスSVMを例に説明する.

$$
\tag{Primal}
\min_w \sum_{i=1}^n[1-y_iw^\top x_i]_+ + \frac{\lambda}{2}\|w\| _2^2
$$

$$
\tag{Dual}
\max_{\alpha\in [0,1]^n} -\frac{1}{2\lambda}\alpha^\top Q\alpha+1^\top\alpha
$$

ただし, $Q_{ij}:=y_iy_j x_i^\top x_j$.

最適解$w^\star$における${w^\star}^\top x_i$の値に応じたサンプルの部分集合を次のように定義する.

$$
\begin{split}
\mathcal{L}^\star&:=\{i \mid y_i{w^\star}^\top x_i < 1 \}, \\
\mathcal{C}^\star&:=\{i \mid y_i{w^\star}^\top x_i = 1 \}, \\
\mathcal{R}^\star&:=\{i \mid y_i{w^\star}^\top x_i > 1 \}.
\end{split}
$$

するとKKT条件から, $\alpha_{i}^\star=-\ell'(y_i{w^\star}^\top x_i)$であり, 次のことがわかる．

$$
\begin{split}
i \in\mathcal{L}^\star&\Rightarrow \alpha_{i}^\star=1, \\
i \in\mathcal{C}^\star&\Rightarrow \alpha_{i}^\star\in[0,1], \\
i \in\mathcal{R}^\star&\Rightarrow \alpha_{i}^\star=0.
\end{split}
$$

$\ell'$は$\ell$の微分を表し, ヒンジの角は-1から0の任意の微分値を取りうる (劣微分).
ややこしい場合は, 平滑化ヒンジ損失の定式化を考えるとよい.

これらの最適解における性質を用いて, $y_i{w^\star}^\top x_i$の値を評価し, $i\in\mathcal{L}^\star$または$i\in\mathcal{R}^\star$とわかれば, そのサンプル$i$に対応する双対変数の値を0または1に固定できる.
すなわち, 最適化すべき双対変数の数を減らすことができる.
主問題を解いている場合は, $i\in\mathcal{L}^\star$ならば損失の$[~] _+$を外すことが可能で, $i\in\mathcal{R}^\star$ならば損失を0にしてサンプル$x_i$を破棄できる.
$[~] _+$が外れると, $i\in\mathcal{L}^\star$と決まったサンプルに関する和をまとめることができるため, それらのサンプルの和のみを保存しておけばよく, 各サンプルを破棄できる.

Safe Screening Rule

$y_i {w^\star}^\top x_i$の値を評価するために, 上で求めた球状の最適解の範囲$\mathcal{B} = \{ w \mid \left\|w-q\right\| _2^2 \le r^2\}$を用いる.
ここで, $v _i:=y_ix_i$とおくと, 評価すべき値は内積値$w^\top v _i$である.
すなわち, 以下の最小化問題と最大化問題を解くことで内積値の範囲が求められる.

$$
\min_{w\in\mathcal{B}} w^\top v_i,~
\max_{w\in\mathcal{B}} w^\top v_i.
$$

この最適化問題は, 単なる球内での内積の最小化/最大化にすぎないため, 次のように解析的に解が求められる.

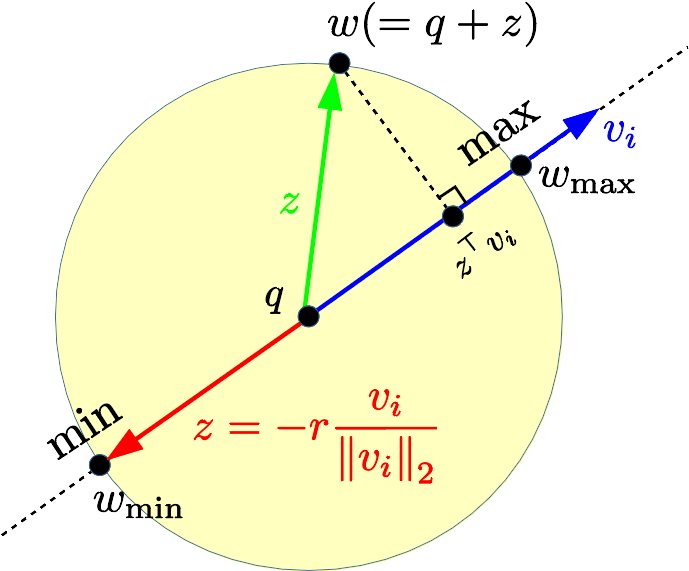
$$
\begin{split}
\min _{w\in\mathcal{B}}&~ w^\top v _i=q^\top v _i -r\|v _i\| _2, \\
\max _{w\in\mathcal{B}}&~ w^\top v _i=q^\top v _i +r\|v _i\| _2.
\end{split}
$$

${w^\star}^\top v _i\ge\min _{w\in\mathcal{B}}w^\top v _i$と${w^\star}^\top v _i\le\max _{w\in\mathcal{B}}w^\top v _i$に着目することで,

$$
\begin{split}
\min _{w\in\mathcal{B}}&~ w^\top v _i=q^\top v _i -r\|v _i\| _2>1
\Rightarrow i\in \mathcal{R}^\star, \\
\max _{w\in\mathcal{B}}&~ w^\top v _i=q^\top v _i +r\|v _i\| _2<1
\Rightarrow i\in \mathcal{L}^\star.
\end{split}
$$

これをScreening Ruleと呼ぶ.
実際にScreeningを行いたいときは, $\mathcal{B}$ にGBやDGBなどを当てはめ, 上記Screening Ruleを各サンプルに関して確認するだけである.

補足

主変数と双対変数

主問題または双対問題のどちらを解く場合も, Screeningを実行でき, 高速化が行える.
たとえばSVMで, 主変数から双対変数を得たいときは,

$$
\alpha_{i}=-\ell'(y_i w^\top x_i)
$$

を実行すればよいし, 双対変数から主変数を得たいときは,

$$
w=\frac{1}{\lambda}\sum_i \alpha_iy_ix_i
$$

を実行すれば良い.
これらの変換はKKT条件から得られるものである. (他の変換を考えてもよい)

Sample ScreeningとFeature Screening

SVMのようにサンプルを除外することを, Sample Screeningと呼ぶ.
一方, LASSOのように特徴を除外することを, Feature Screeningと呼ぶ.
これらの定式化においては, Sample Screeningでは主変数$w$のバウンドが必要となり, Feature Screeningでは双対変数$\alpha$のバウンドが必要となる.
双対変数におけるバウンドの導出も主変数のバウンドと同様に行える.

具体的には, 双対問題においてL2ノルムが現れればバウンドを作れるので, 以下の定理から損失関数を平滑関数にすればよい.

定理 $f$が$\mu$-強凸関数であることと, その共役関数$f^*$が$1/\mu$-平滑関数であることは同値.

定義 ($\gamma$-平滑関数) 凸関数$f$が$\|\nabla f(x)-\nabla f(y)\|\le \gamma \|x-y\|$であるとき$\gamma$-平滑関数と呼ぶ.

正則化パス計算とDynamic Screening

バウンドにはある実行可能解が必要であるが, その解の質によってScreening性能が変わる.
質が良いほどScreeningでき, より高速化につながる.
そのため, Screeningの実験では, 以下のようにハイパーパラメータ$\lambda$を変えていき, 一つ前の解を利用してScreeningを試みる事が多い.

このように, 正則化係数を変えていき, 順番に解を求めていくことを正則化パス計算と呼ぶ.
Screeningを学習前と学習中行う場合で区別する場合, 学習中に行うScreeningをDynamic Screeningと呼ぶ.
学習前に行うScreeningに特に決まった名前はないため, ここでは正則化パスScreeningと呼ぶことにする.
学習前と学習中を分けたのは, 特に学習前にのみ使える正則化パス計算に特化したバウンドが存在するためである.
(GBとDGBは学習前/学習中のどちらにも使える)

正則化パス計算では, 実行したい$\lambda$の区間$[\lambda_{\rm end}=\lambda_{T}, \lambda_{\rm begin}=\lambda_{1}]$を対数スケールで$T$等分することが多い. (大きい$\lambda$から小さい$\lambda$へ徐々に変化させる)
このとき, $\lambda$の更新式は$\lambda_{t+1}=R\lambda_{t}~(t=1,\ldots,T-1)$で表現される.
ただし, 減衰率$R=(\frac{\lambda_{\rm end}}{\lambda_{\rm begin}})^{\frac{1}{T-1}}$である.
例: 区間$[10^{-3}, 10^3]$を7分割すると, $R=(\frac{10^{-3}}{10^3})^\frac{1}{7-1}=0.1$となり, $\lambda=[10^{3}, 10^{2}, 10^{1}, 1, 10^{-1}, 10^{-2}, 10^{-3}]$の順で実行される.

機械学習の高速化手法Safe Screeningを解説