はじめに
こんにちは、この記事の著者はPC初心者がプログラミングの勉強のために書いたものとなっています。ご了承ください。今回は、単回帰分析において用いられている、最小二乗法について、pythonを用いて解説します。
線形単回帰
機械学習の最も基本的なモデルである「単回帰」では、1つの数値x(説明変数)から、1つの数値y(目的変数)を予測します。このとき、xの値からyの値を求めるには、
y = ax + b
の式に代入すれば、yの値が算出できそうです。aとbの値を求めるために使うものが、「学習用データセット」となります。ここでは、
xが1のとき、yは10
xが3のとき、yは14
xが6のとき、yは20
を「学習用データセット」とします。xが7のときのyの値を予測します。まず、学習用データセットのxとyの値で散布図を描いてみます。
import matplotlib.pyplot as plt
import numpy as np
xdata = np.array([1, 3, 6])
ydata = np.array([10, 14, 20])
plt.scatter(xdata,ydata)
plt.xlabel("x")
plt.ylabel("y")
plt.show()
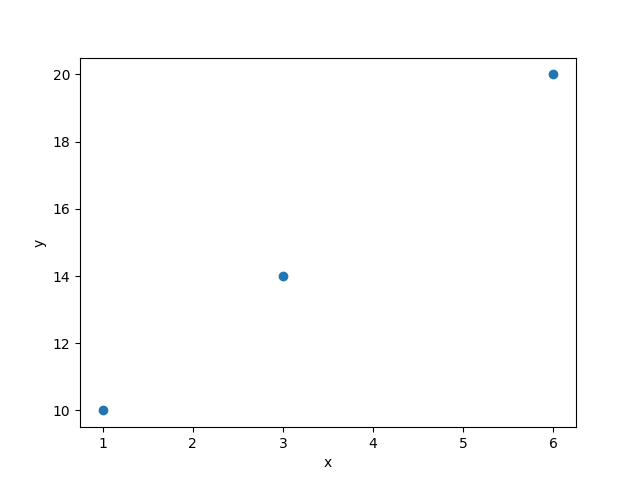
プロットした点と点は線で結べそうです。
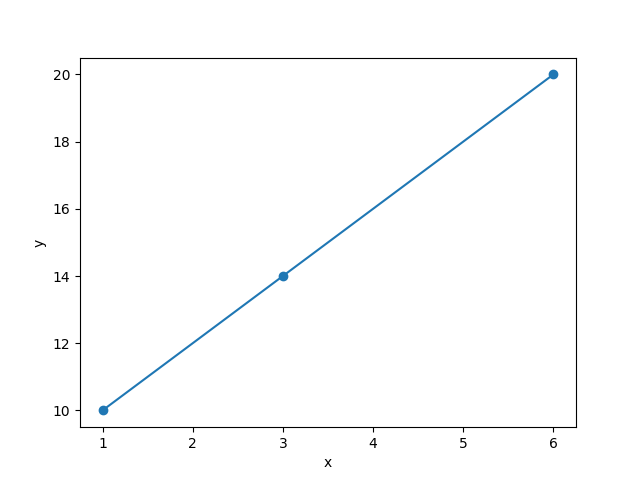
結ぶことが出来ました。連立方程式を使えば、y = ax + bのaとbの値が算出できそうです。実際に求めてみるとa = 2, b = 8となります。これで、yの値の予測式がy = 2x + 8となることが分かりました。この式にxの値を代入すれば、yの値は22ということが分かりました。
上記のパターンでは、「学習用データセット」によってプロットした点で線を引くと、全ての点を通りましたが、現実はこう上手くはいきません。たとえばコード1のxdata, ydata部分を
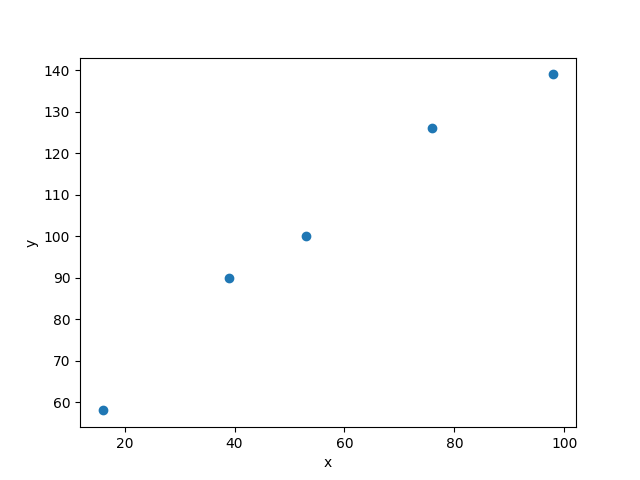
xdata = np.array([16, 76, 39, 53, 98])
ydata = np.array([58, 126, 90, 100, 139])
先ほどのように、全ての点を通るような一次関数は無さそうです。しかし、5つの点と近似するような一次関数の式は描けそうです。
最小二乗法
では、5つの点と近似するような一次関数の式を求めるにはどうすれば良いのか?答えは一次関数の式と点の距離が最小となるような式を探せばいいのです。予測式を
y = ax + b
「学習用データセット」を下記のように文字で表します。
xdata = x_1, x_2, \cdots x_{i-1}, x_i\\
ydata = y_1, y_2, \cdots y_{i-1}, y_i
一番目の要素と予測式のy軸方向の距離は
(ax_1 + b) - y_1
で求めることが出来ます。この値は負の値をとることもあるので、2乗して正の値にします。
(ax_1 + b - y_1)^2
残りの点でも同じことをすれば、データ点と予測式の距離を求めることが出来ます。今回は、全ての点と近似するような一次関数の式を求めることが目的なので、データ点と予測式の距離が最小値になれば良いです。
(ax_1 + b - y_1)^2 + (ax_2 + b - y_2)^2 + \cdots(ax_i + b - y_i)^2
上記の関数をL(a,b)として、総和記号Σを使って(nは要素数)、
L(a,b) = \sum_{i=1}^{n} (ax_i + b - y_i)^2\\
と、表すことができます。微分して値が0となる点では傾きが0なので、極値になります。L(a,b)のa^2とb^2の係数は必ず正の値になるので、L(a,b)のグラフは常に「下に凸」となります。よって、関数L(a,b)が最小値をとるようなa,bを探すには、(L(a,b)を微分した値) = 0 になれば良いわけです。関数L(a,b)をaまたはbで偏微分します。
\frac{∂L(a,b)}{∂a} = \sum_{i=1}^{n} (2x_i^2a + 2x_ib - 2x_iy_i) = 0 \cdots (1)\\
\frac{∂L(a,b)}{∂b} = \sum_{i=1}^{n} (2b + 2x_ia - 2y_i) = 0\cdots (2)\\
が、成り立てばよいです。次に、二つの式を変形します。まず(2)の式から、
\frac{∂L(a,b)}{∂b} = \sum_{i=1}^{n} (2b + 2x_ia - 2y_i) = 0\\
\sum_{i=1}^{n} (b + x_ia - y_i) = 0\\
\ -\sum_{i=1}^{n} y_i + a\sum_{i=1}^{n} x_i + bn = 0\\
\ -\frac{1}{n}\sum_{i=1}^{n} y_i + a\frac{1}{n}\sum_{i=1}^{n} x_i + b = 0\\
\ b = \frac{1}{n}\sum_{i=1}^{n} y_i - a\frac{1}{n}\sum_{i=1}^{n} x_i
xdataとydataの平均値を
\bar{x} = \frac{1}{n}\sum_{i=1}^{n} x_i\\
\bar{y} = \frac{1}{n}\sum_{i=1}^{n} y_i\\
とすると、
b = \bar{y} - a\bar{x} \cdots (3)\\
次に(1)の式を変形します。
\frac{∂L(a,b)}{∂a} = \sum_{i=1}^{n} (2x_i^2a + 2x_ib - 2x_iy_i) = 0\\
\sum_{i=1}^{n} (x_i^2a + x_ib - x_iy_i) = 0\\
a\sum_{i=1}^{n} x_i^2 + b\sum_{i=1}^{n} x_i - \sum_{i=1}^{n} x_iy_i = 0
(3)の式を変形した式を代入します。
a\sum_{i=1}^{n} x_i^2 + (\bar{y} - a\bar{x})\sum_{i=1}^{n} x_i - \sum_{i=1}^{n} x_iy_i = 0\\
a\frac{1}{n}\sum_{i=1}^{n} x_i^2 + \bar{y}\frac{1}{n}\sum_{i=1}^{n} x_i - a\bar{x}\frac{1}{n}\sum_{i=1}^{n} x_i - \frac{1}{n}\sum_{i=1}^{n} x_iy_i = 0\\
a\frac{1}{n}\sum_{i=1}^{n} x_i^2 + \bar{x}\bar{y} - a\bar{x}^2 - \frac{1}{n}\sum_{i=1}^{n} x_iy_i = 0\\
a(\frac{1}{n}\sum_{i=1}^{n}x_i^2 - \bar{x}^2) = \frac{1}{n}\sum_{i=1}^{n} x_iy_i - \bar{x}\bar{y}\\
a(\frac{1}{n}\sum_{i=1}^{n}x_i^2 - 2\bar{x}^2 + \bar{x}^2) = \frac{1}{n}\sum_{i=1}^{n} x_iy_i - \bar{x}\bar{y}\\
a(\frac{1}{n}\sum_{i=1}^{n}x_i^2 -2a\bar{x}\frac{1}{n}\sum_{i=1}^{n} x_i + \bar{x}^2) = \frac{1}{n}\sum_{i=1}^{n} x_iy_i -2\bar{x}\bar{y} + \bar{x}\bar{y}\\
a\frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2 = \frac{1}{n}\sum_{i=1}^{n}((x_i - \bar{x})(y_i - \bar{y}))\\
a = \frac{\frac{1}{n}\sum_{i=1}^{n}((x_i - \bar{x})(y_i - \bar{y}))}{\frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2}\\
回帰係数aは(x,yの共分散)/(xの分散)で算出できるようです。切片bは、(3)の式に回帰係数aを代入すれば、算出することができます。これで、a, bの値が分かったので、予測式から未知の値を予測することができます。
実際に使ってみる
コード2のデータにおいて、x = 70のときのyの値をpythonで計算して、予測してみます。(numpyの関数を使用します)
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
xdata = np.array([16, 76, 39, 53, 98])
ydata = np.array([58, 126, 90, 100, 139])
x_mean = np.mean(xdata)
y_mean = np.mean(ydata)
# np.mean 平均値を求める
x_var = np.var(xdata)
# np.var 分散を求める
xy_cov = np.cov(xdata, ydata, rowvar=1)[0][1]
# np.cov xdataとydataの共分散を求める
a = round(x_var/xy_cov, 1)
# 回帰係数
b = round(y_mean - a*x_mean, 1)
# 切片
print("回帰係数", a)
print("切片", b)
print("予測式 y = {}x + {}".format(a, b))
# 計算結果の表示
回帰係数 0.8
切片 57.5
予測式 y = 0.8x + 57.5
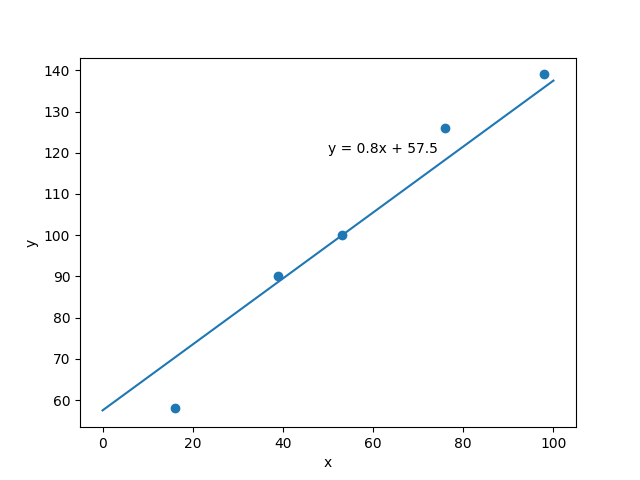
回帰係数、切片、予測式を求めることができました。予測式をデータの散布図に当てはめてみます。 以下のコードを書き足します。
x = np.linspace(0, 100, 1000)
y = a*x + b
plt.plot(x, y)
plt.text(50, 120, "y = {}x + {}".format(a, b))
plt.scatter(xdata, ydata)
plt.xlabel("x")
plt.ylabel("y")
plt.show()
5つの点と近似するような一次関数の式が書けました。予測式に代入すると、x = 70のときの y の値は113.5 と予測できました。
参考までに…
最小二乗法の公式の導出
https://analytics-notty.tech/derivation-of-least-squares-equation/
python version
3.9.2