注)ちょくちょくアップデートしています
知人とskypeしている最中にふざけて死刑!死刑!とか言っていたら気になったので。
日本は死刑が廃止された事がないらしく、推定は極めて難しい。過去の研究は1990年ごろが初でそれまで無根拠だったのかと(行政全般だが)文化の質を疑うが、この問題は(数学を使わない)経済学や心理学など多方面で同様で定義や論理のステップが歴史的経緯やエラい人の発言で補強されるっぽいw
https://umoregicho.hatenablog.com/entry/2018/11/06/013852
によると、1990年と1993年の回帰モデルの推定は、それぞれ抑止効果ありとなしだが、事件数が根本的に単位根を含むっぽく無効と言われている。2017年頃のVARを用いた研究でもなしとなっているがこの文献は無料では読めなかった。
その他、アメリカが州ごとに死刑制度が違うのでDIDで推定した論文があり、それは10-20%程度効果ありだった記憶だが、日本の場合は廃止されたことがないので厳しそうだが、時系列的な方法でチャレンジしてみる。
データは
https://www.crimeinfo.jp/data/toukei/statistics_05-2/
やe-statの
https://www.e-stat.go.jp/dbview?sid=0003274121
より。
死刑宣告率 をその年の死刑確定数/(死刑確定数+無期懲役確定数)
とし、これが次の年の殺人事件件数に影響すると仮定。
宣告率と事件件数は一見相関があるが、そのままだと単位根検定をリジェクトできなく、回帰も効果ありだが、信頼できない。事件数がランダムウォーク、つまりかなり前の事件を引きずっている可能性があるって以外なきがしますが、ヤクザの報復とか???
状態空間モデル,stanで計算、事件数の対数をyとし
抑止力=t-1からt-6くらいまでの死刑宣告率の線形結合。それ以上はサンプル不足で推定が安定しなかったです。
年tの殺人事件数〜normal(年tのtrend+抑止力)
として
トレンドは1階差分で3年前分の宣告率の影響を見る、すなわち
yokusi[t]~normal(dot(b,dp_per))
y[t]~normal(trend[t]+yokusi,sigma)
と事件数yを、隠れ変数の「平均」trendと後ろの抑止力に分解する
library(tidyverse)
df=read.csv("data")
df[,3]=as.numeric(str_remove(df[,3],","))
df$死刑確定[is.na(df$死刑確定)]=3
df$dp_per=df$死刑確定/(df$死刑確定+df$無期)
# y=exp(trend)*exp(yokusi)
library(rstan)
y=log(df$殺人)
N=length(y)
n_b=6 #何年前の宣告率まで見るか
sdat=list(y=y,N=N,n_b=n_b,
dp_per=df$dp_per)
rstan_options(auto_write=TRUE)
options(mc.cores=parallel::detectCores())
fit=stan(file ="yokusi.stan",
data=sdat,
init=function() { list(trend=y,
b=rep(0,n_b)
)},warmup=1000,iter=3000,chains=3)
d=get_posterior_mean(fit,par="trend")
d=d[,ncol(d)]
get_posterior_mean(fit,par="sigma")
get_posterior_mean(fit,par="s_trend")
b=exp(get_posterior_mean(fit,par="b")[,4])
resid=exp(get_posterior_mean(fit,par="resid")[,4]) #y/y_pred
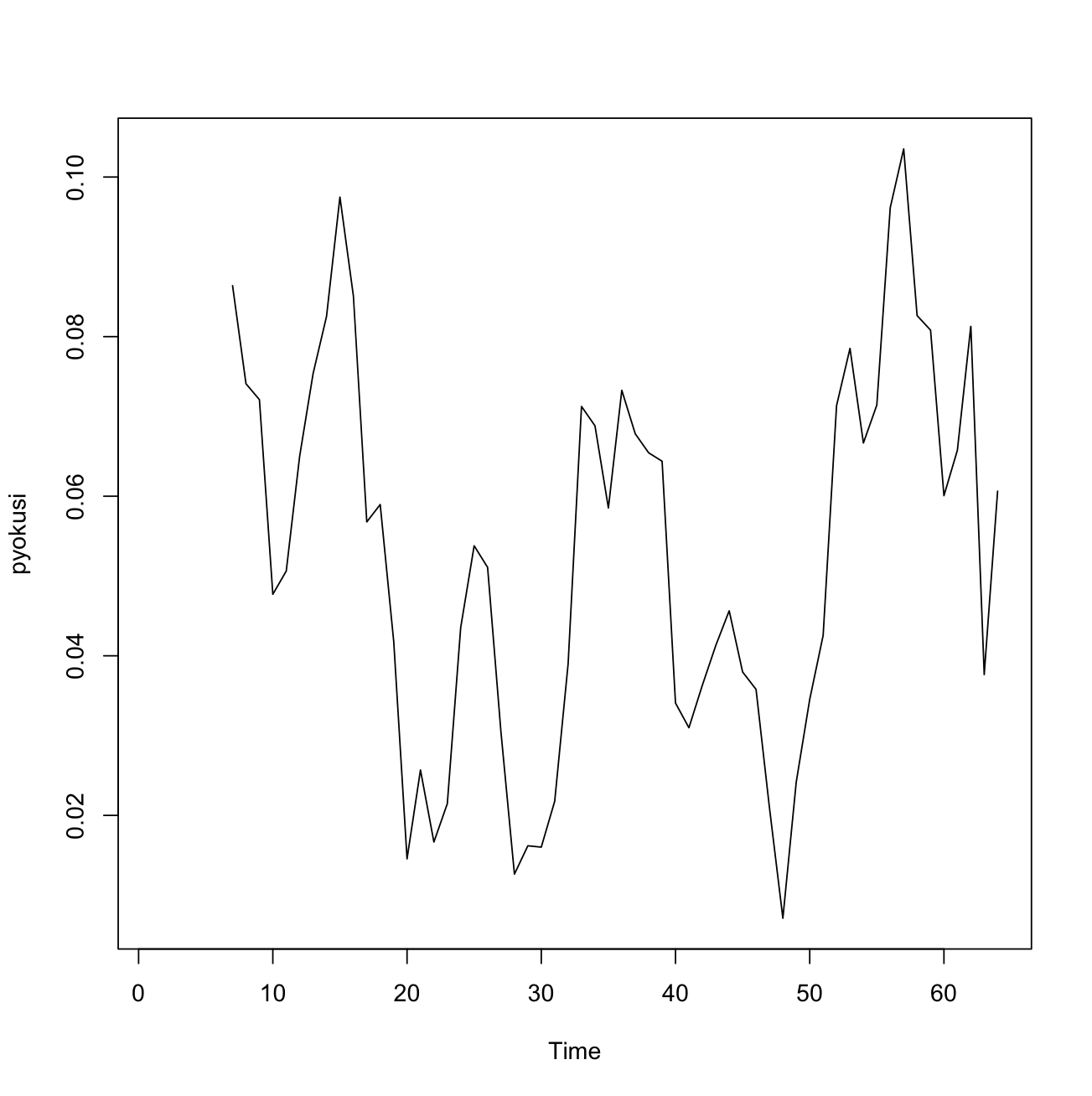
pyokusi=get_posterior_mean(fit,par="pyokusi")[,4]
ts.plot(pyokusi)
print(b)
plot(b)
#summary(fit)
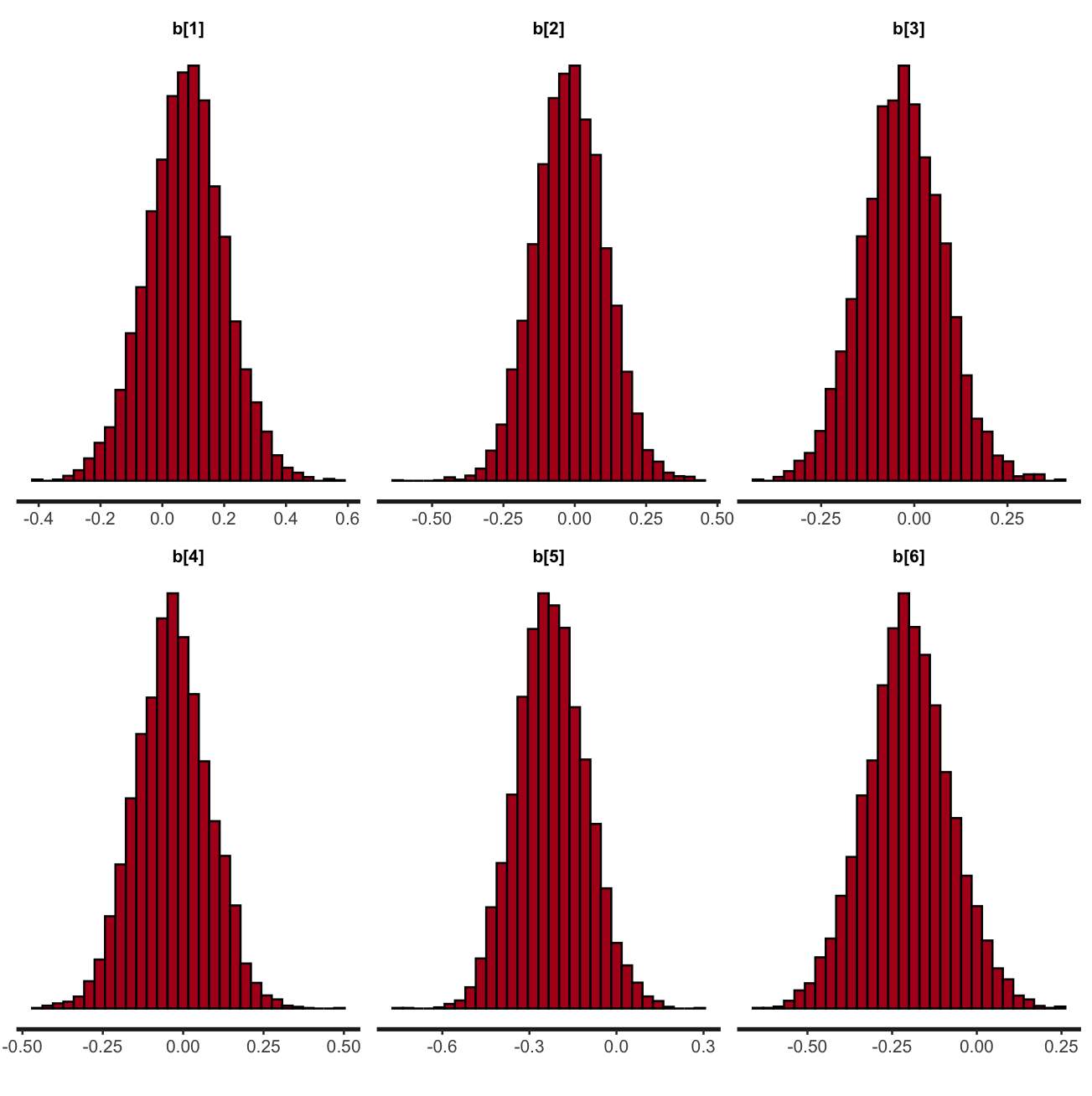
stan_hist(fit,"b")
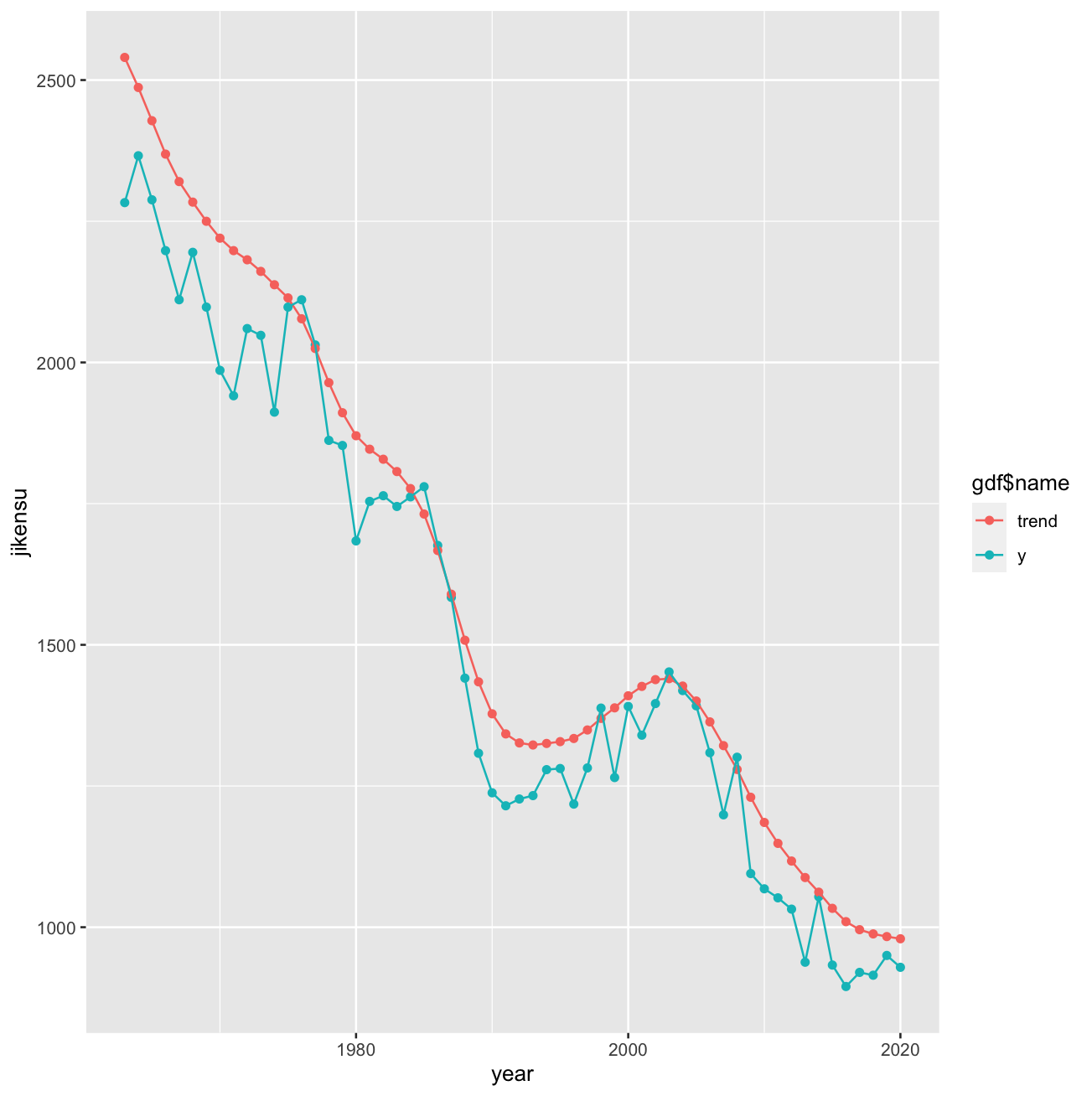
tdf=data_frame(time=df$年,y=exp(y),trend=exp(d))
tdf=tdf[(n_b+1):nrow(tdf),]
gdf=pivot_longer(tdf,c("y","trend"))
qplot(gdf$time,gdf$value,col=gdf$name)+geom_line()+xlab("year")+ylab("jikensu")
ts.plot(df$dp_per)
stanのコードは
data{
int N;
int n_b;
real y[N];
vector[N] dp_per;
}
parameters {
real sigma;
real trend[N];
real s_trend;
vector[n_b] b;
}
model{
vector[n_b] tmp;
b~normal(0,0.3);
for(t in 3:N){
trend[t]~normal(2*trend[t-1] -trend[t-2],s_trend);
}
for(t in (n_b+1):N){
tmp=dp_per[(t-n_b):(t-1)];
y[t]~normal(trend[t]+dot_product(b,tmp),sigma);
}
}
generated quantities {
real pyokusi[N];
real resid[N];
for(t in (n_b+1):N){
pyokusi[t]=1-exp(dot_product(b,dp_per[(t-n_b):(t-1)]));
resid[t]=y[t]-(trend[t]+dot_product(b,dp_per[(t-n_b):(t-1)]));
}
}
推定したexp(bの平均)、1だと効果なし。前年がプラス?
一番右の6年前は0.81なので、宣告率10%で0.19*0.10で2%程度の抑止効果という意味。
b[1] b[2] b[3] b[4] b[5] b[6]
1.0792408 0.9844395 0.9686918 0.9670788 0.7994486 0.8154978
今の所の結論はだいたい6%くらい抑止する効果があるが前年の宣告率では宣告率の平均が0.15くらいなので
exp(0.15*0.07)=1%くらい増えるという感じですかね???
死刑確定の定義がイマイチ理解できていなく、事件発生とのモデルは他にも色々試す必要があり。
死刑宣告率→事件件数の間の交絡として、何かありましたら教えてくれると幸いです。GDPや生活保護捕捉率やなのがある文献は見た記憶ですね。