はじめに
完全に自分メモなので、それでも良ければ読んでやってください。途中のものなどもあります。随時更新予定。
ML,DLやデータサイエンスの勉強をがむしゃらにしてきた。
いろいろと知識が分散しすぎているのでまとめて行こうと思う。キャパオーバー。
ただ、数式をちゃんと説明したりなどをやっていると疲れるので自分が持っているイメージを重視して書きます。
詳細を知りたい人は本などで勉強してください。
学習に使った本は、以下4冊です。(他にもあるけど後で。)
- 新米探偵データ分析に挑む（実例を、数式とかは省いているので、普通にラノベ感覚で読める。全く知らない人にお勧め。）
- 統計検定２級(天才じゃないと一読で理解は無理、ただ体系的な理解を得るという意味だけでは良い本。)
- 道具としてのベイズ統計(道具としてシリーズ、やはり分かりやすい。)
- 確率モデル(統計より先の話、マルコフ連鎖とか確率微分方程式とか、証明などがなく数学科卒でない自分には助かる。)
目次
統計と言ってもいろいろな分類がある。
- 記述統計学
- 数理統計学
- 推測統計学
- 従来の推測統計学(推定や検定）
- ベイズ統計学
- 多変量解析
記述統計
データを整理することに重点を置く分野。
データを簡単に簡単な数値にまとめたり、可視化や扱いやすくする。
数理統計学
データを分析して、データの構造や本質などを考える。
推計統計学
データを標本として、その母集団の特性値を推定する。
多変量解析学
データ構造を解析して、変数間の相関を調べる。
ベイズ統計学
本記事のメインの予定。
主観統計学と呼ばれ、ベイズ更新により確率分布が随時更新される。
本概念は、迷惑メールのフィルタから自動運転にまで利用されているものである。
記述統計学
結構高校数学Aで学べる内容が多い。
基本的に、データの特徴を示す。
（全てを記載するのは無理なので。念のため記載。）
例えば、テストを行い点数
- 数学 70,72,72,74,75,75,75,77,78,80
- 国語 50,52,55,55,58,80,92,94,95,97
このデータ群はどういう特徴を持つのだろうか？という疑問に対する回答を提示してくれる。
理論編
テストの例を考えるにあたり、理論をまとめておく。
平均
全てのデータの和をデータ数で割る。
これにより、重心のようなものが大まかに分かる。
ただし、データの偏りは一切わからないので平均のみで判断するのは軽率。
その他の代表的な値は、最頻値(同値が一番多い値)、中央値(データの真ん中の値)
平均 μ = \frac{1}{n} \sum_{i=1}^n x_i
分散、標準偏差、標準化
全てのデータから平均値を引いた自乗の和をデータ数で割る。
これにより、データの偏りの大きさが分かる。
（ありえない話を続けると、山が２つある場合は、分散に大きな値を持つが、平均値に多くの測定値がある場合は小さな値になる。）
またデータの値が大きい場合や小さい場合で比較しずらいので標準化を行う。
分散 σ = \frac{1}{n} \sum_{i=1}^n (x_i - μ) ^2
標準偏差 s = \sqrtσ
標準化 ｚ_i = \frac{x_i - μ} {σ}
変動係数
標準偏差を平均で割る。(上記の標準化と同じ)
分散は構造上、値が大きいデータと小さいデータを比べる場合に前者が大きくなる。(データの偏りがなくても)
多変数時、各変数の標準化された分散を見れる。
変動係数 cv = \frac{s}{μ}
共分散、相関係数
多変数間の関係を計算する。
共分散 s_{xy} = \frac{1}{n} \sum_{i=1}^n (x_i - μ_x)(y_i - μ_y)
相関係数 r_{xy} = \frac{s_{xy}}{s_xs_y}
実践(python)
理論は終わったので実際にテストデータの特徴を計算する。
可視化(seaborn)
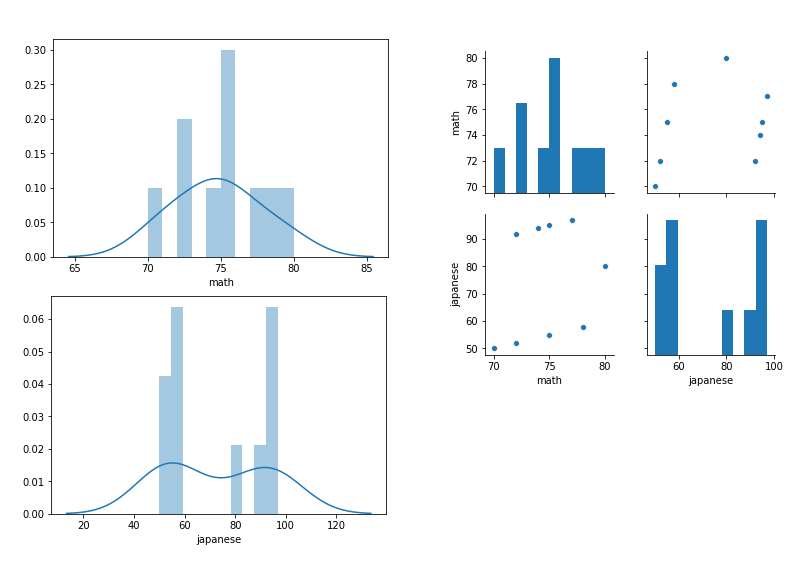
数学と国語のデータをヒストグラムにした。数学は山が1つ、国語は山が2つあることが分かる。
また、数学と国語のペアプロットをした。特に強い相関は感じない。つまり数学が得意だと国語が不得意などという一般的な特徴はない。
(これは、山を2つ作るために、国語データを作成するときに数学データに-20,+20と追加したせい。)
集計(pandas)
pandasではdescribeで特徴(平均、標準偏差、最大、最小、中央値、四分位)を計算してくれる。covは共分散、corrは相関係数。
(残念ながら変動係数はコマンドないけど計算は簡単なので)
集計結果から以下のことが分かる。これは可視化により想像はつく内容である。（つまり逆に集計から大まかな分布は予想できる。)
- 平均はほぼ同じだが分散値が全く異なることから、数学の方がシャープなグラフとなる。
- 相関係数から数学と国語にはほぼ相関がないことが分かる。
集計から山が２つあることは、もしかしたら四分位の分布から分かるかもしれない？が、
可視化と集計の両者によりテスト結果について理解を深められた。
これが記述統計の提示するものである。
推測統計学
記述統計は、データの特徴を抽出することができる。
しかし、データ数が1億の場合に上記の計算は現実的だろうか。全データで平均を取ることが生産的かという疑問も生まれる。
推測統計学は上記の問題に対して、推定と検定という手法により回答を用意している。実例として工場の品質管理などに応用されているものである。
推定
点推定と区間推定があるが、基本的に後者を利用する(はず)
サンプル(標本)から母集団の特徴を推測できる。
検定(仮説検定)
母集団に対する仮説の検証をサンプル(標本)から行う。
さっそく実践しよう!
例として先ほどの数学を拡張した問題を考える。
1クラス100人としてテストを行いランダムに点数を公開した結果が70,72,72,74,75,75,75,77,78,80の場合に、感覚的に考えてこのクラスの平均が40点になりえるだろうか?残り90人が35点程度でランダムに高得点の人だけを取り出せたと考えればありえるが..本当だろうか?
仮説:クラスの平均点は40点である。
母平均を求める
1クラス(100人)を母集団、10人を標本として考える。その時の母集団の平均を推定します。
母分散が既知(分散=25)の場合-z検定
どんなときに既知なんですか？既知なら母平均分かってるんじゃないんですか？という疑問は無視する。
また、母集団は正規分布に従うものとする。以下の不等号式が成り立つ。
\bar{x} - z_{α/2} × \frac{σ}{\sqrt{n}} < μ < \bar{x} + z_{α/2} × \frac{σ}{\sqrt{n}}
\bar{x}はサンプル平均,zは標準正規分布の累積,αは有意水準
テストについては記述統計の数学と同じデータなので、
n = 10, 平均点は74.8, 標準偏差は3.0(ただし今回は母集団の分散が分かっているので未使用)、分散は25と既知である。
またα=0.05とすると,z=1.96となる。(説明は正規分布でする予定。)
74.8 - 1.96 × \frac{25}{\sqrt{10}} < μ < 74.8 + 1.96 × \frac{25}{\sqrt{10}}
59.3 < μ < 90.3
という結果が得られる。だいたい平均点から15点程度の幅を持たせた区間となる。
従って、95%信頼区間(α=0.05)が得られた。95%信頼区間とは上記のサンプリングを100回やれば95回は母平均がその区間が含まれているということを示す。
結論：仮説は95%信頼区間外であるため、平均点は40点という仮説は否定される。