メリークリスマスですね。いろいろと力不足だとは思いますが、担当させていただきます。
今回紹介する論文は、NeurIPS2020から選んだ論文です。タイトルは、「Learning from Failure: Training Debiased Classifier from Biased Classifier. Advances in Neural Information Processing Systems」です。文献情報、論文へのリンクは下に乗せておきます。1
スライド見る方が好きな人はこちらどうぞ
この記事に必要な前提知識
基礎的な機械学習の知識は必要な気はしますが、是非読んでいってください。クロスエントロピーについて理解していれば大丈夫だと思います。
概要&問題設定
論文では、バイアスがかかったデータセットから、バイアスが除かれたモデルを得るための手法を提案しています。こういったバイアス取り除く系の論文では、バイアスがかかったデータセットというのは色付きMNISTがまずよく用いられます(多分)。
MNISTに色をつけたデータセットです。例えば、赤色の0ばかりのデータで学習させると、テスト時に赤色以外(黄色とか、青色とか)の0への分類精度が著しく下がってしまいます(データセットにバイアスがかかっているからです。つまり、「赤色なら0」という風に学習してしまう)。
この論文では、CIFAR-10にバイアスをかけたものも用いています。例えば図の左側は飛行機の画像ですが、白い線のようなノイズがのっています。このようなデータばかりで学習させると、ノイズのない画像を入れたときの精度が著しく下がります(つまり、「飛行機の形状」を学ぶのではなく、「画像に白い線のノイズがある→それは飛行機」と学習してしまうわけです)。
論文の問題設定としては、このようなバイアスがかかったデータセットに対して、バイアスのかかっていないデータに対してもきちんと分類できるようにするという設定です。この問題に対して、先行研究では人の事前知識をつかうというアプローチをとっていました。この論文は、事前知識なしにこの問題に対処する方法を提案しています。
手法の概要
先にアルゴリズムをのせてしまいます、すごくシンプルです。

肝は2行目と5、6行目です。
2つCNNなどのニューラルを用意して(論文では確かRes-Net)、それぞれ更新していくというアプローチです。5,6行目の赤枠を見るとわかりますが、lossの取り方が2つのニューラルで違います。手法のイメージ図は以下の通りです。
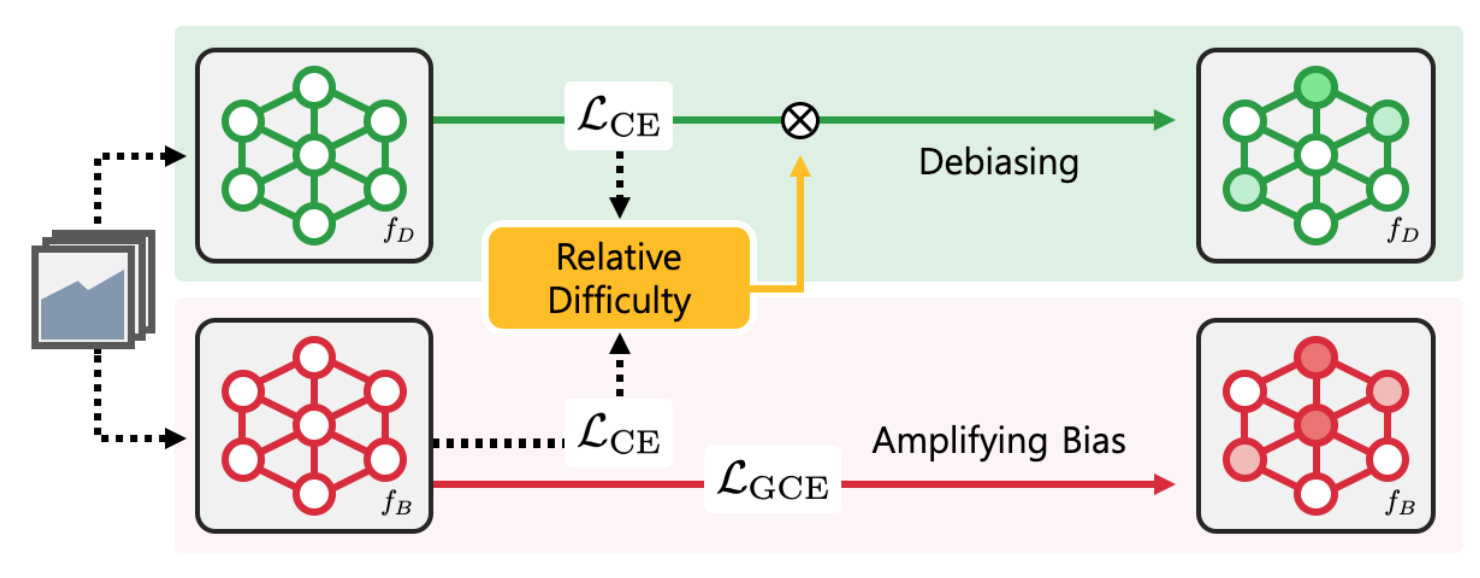
バイアスをわざと学習するためのニューラル$f_{B}$と、本来得たいバイアスがかかっていない良いモデル$f_{D}$を学習していく考えです(BはBiasedのB,DはDebiasedのDです。考え方としては、GANみたいな感じともいえます)。アルゴリズムの5行目からわかるように、$f_{B}$に対してはGCEというlossを取っています。これはGeneralized Cross Entropyの略で、式としては以下のようなものです。
$$
\operatorname{GCE}(p(x ; \theta), y)=\frac{1-p_{y}(x ; \theta)^{q}}{q}
$$
$y$は正解ラベル、$p(\cdot)$はソフトマックス後のニューラルの出力、$q$は(0,1]をとるハイパーパラメータです。極限を考えると、
$$
\lim _{q \rightarrow 0} \frac{1-p^{q}}{q}=-\log p
$$
であることから、通常のクロスエントロピーを含んでいます(ロピタルの定理を用いて容易に確認できます、GCEと呼ばれる理由です、多分)。これを用いると勾配の式が
$$
\frac{\partial \operatorname{GCE}(p, y)}{\partial \theta}=p_{y}^{q} \frac{\partial \operatorname{CE}(p, y)}{\partial \theta}
$$
となります。つまり、高い確信を持っている方にモデルが増幅するわけです(イメージ図のAmplifying Biasを下手に訳しました)。これによって、$f_{B}$はバイアスがかかったモデルになるように学習されます。鋭い方、私の下手な説明も理解できる理解力の高い方はこの時点で、「え、なんでそうなんの?」となると思います。実はこの論文では事前実験の観察から、悪いバイアスはすぐに学習されることを観察しています(c.f. 論文中の2.3)。
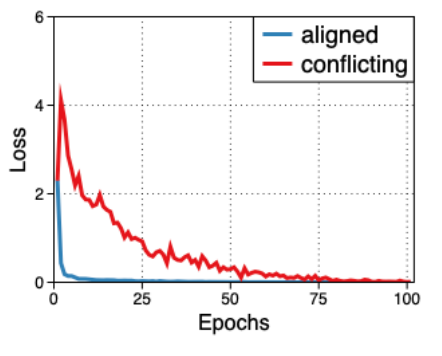
alignedがバイアスデータ、conflictingがそうでないデータを表しています。図から、早い段階でalignedのlossが落ちているのがわかります。したがって、GCEを使うことでバイアスのかかったモデルを容易に学習することができるのです(早い段階からバイアスのかかったデータに対して高い確信$p_{y}^q$を持つため)。
バイアスのかかっていない良いモデル$f_{D}$に対しては、アルゴリズム6行目からわかるように、通常のクロスエントロピー(CE)に対して$\mathcal{W}(x)$をかけています。これは、以下のような式で計算されます。
$$
\mathcal{W}(x)=\frac{\operatorname{CE}\left(f_{B}(x), y\right)}{\operatorname{CE}\left(f_{B}(x), y\right)+\operatorname{CE}\left(f_{D}(x), y\right)}
$$
つまり、$f_{B}$が苦戦しているデータ(つまり、バイアスではないデータ、少数のデータ)に対しては分子が大きくなるため、そういったデータに対してうまく分類できるように学習されます(「赤いから数字の0」、という推論ではなく、「丸みがあるから0」という風になるよう方向付けされます。本当にそうなっているかは知りませんが)。
以上が手法についての説明です。わかりづらくて大変申し訳ありませんが、もし理解していただいた方は、タイトルである「Learning from Failure(失敗から学ぶ)」の意味が理解できるかと思います。
実験
上で述べた色付きMNIST、バイアス付きCIFAR-10に加えて、CelebAとBARというデータセットで実験しています。このBARというデータセットは、この論文で提案されているデータセットです(リンク)。MNISTとCIFAR-10に関してだけ紹介します。CelebAとBARに関しても良い結果が出ているという主張です。以下、MNISTとCIFAR-10に対する結果です。
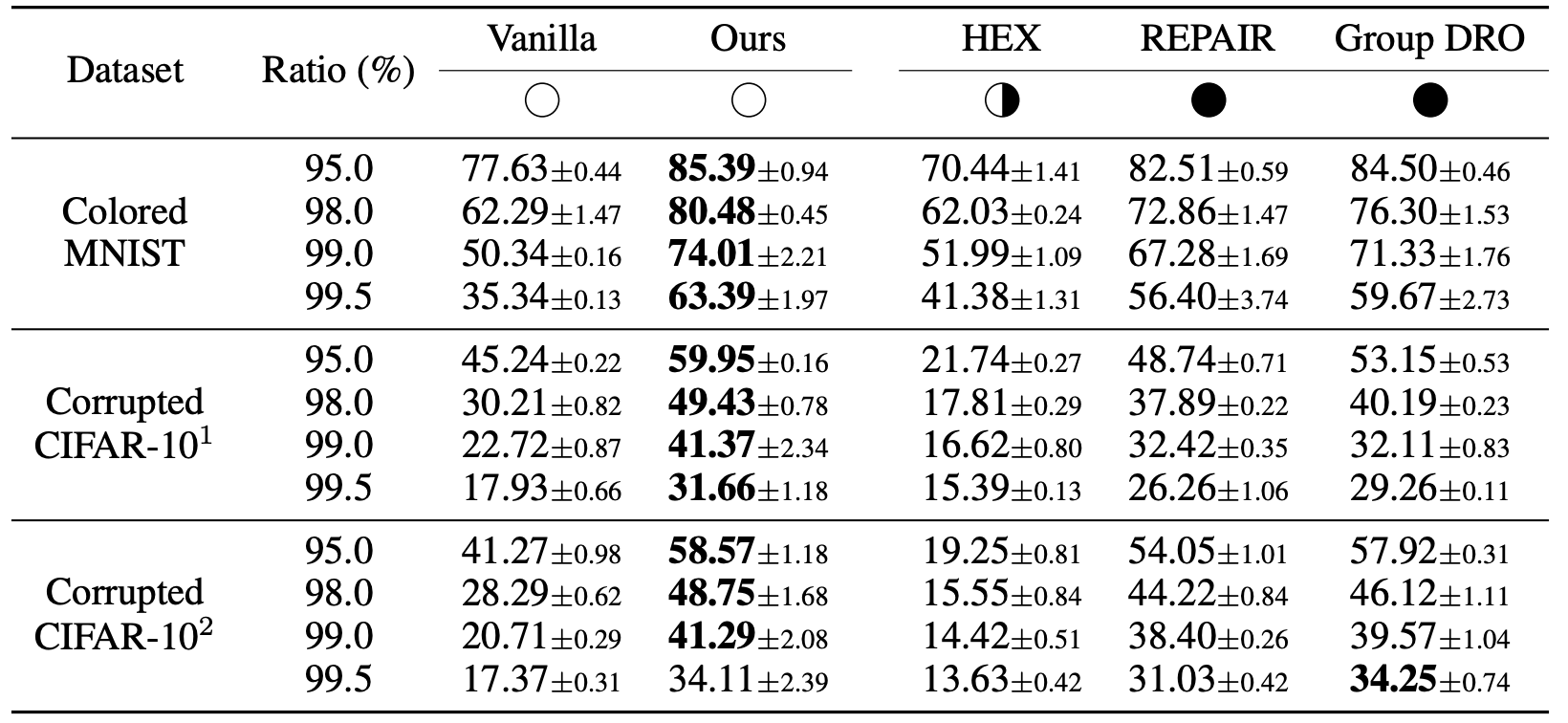
図の見方について説明します。Ratio(%)というのは、バイアスデータの割合です。例えば、95.0なら、学習用のMNIST画像の数字0の95%が赤色、残り5%は赤以外、といった意味です(他の数字も同様)。つまりRatioが100%に近づくほど、バイアスデータが増えるので、バイアスを取り除くのは難しくなりそうだといえます。また、Vanillaはそのまま学習して評価した場合、HEX,REPAIR,Group DROは比較手法です。○、⚫️、半分白半分黒がありますが、事前知識がいるかどうかを表しています。⚫️は人の事前知識・労力が必要な先行研究の手法、半分白半分黒は半分くらい人間の知識がいるということですが、原著を読んでいないのでよくわかりません。とにかく、提案手法(Ours)は全く人間の事前知識や労力はいらんよと言っています(○)。
結果からわかるように、シンプルなアルゴリズムですが、ほとんどの設定で比較手法を上回っていることが見て取れます。
まとめ
この手法を使えば、バイアスがかかったデータセットからフェアな良いモデルが得られる、かもしれませんね。手法自体はシンプルで、理解はしやすかったのではと思います。
最後まで読んでいただきありがとうございました。良いクリスマス、良いお年を。
補足
著者のコードがここにあがっています.
-
Nam, J., Cha, H., Ahn, S., Lee, J., & Shin, J. (2020). Learning from Failure: Training Debiased Classifier from Biased Classifier. Advances in Neural Information Processing Systems, 33. https://arxiv.org/pdf/2007.02561.pdf ↩

