はじめに
本記事で分かること
- 最小二乗法の概要
- 最小二乗法のMATLABを用いた実装プログラムと出力結果の例
- 最小距離二乗法の概要
- 最小距離二乗法を導出する数式
- 最小距離二乗法のMATLABを用いた実装プログラムと出力結果の例
参考文献について
最小距離二乗法という名は、おそらく正式名称ではありませんが、
“最小距離2乗法による回帰直線の求め方”(永島弘文,大館孝幸,荒井太紀雄,1986)
上記文献にて、この名称の記載があり、名称および解法についてこちらを参考にさせていただきました。
この方法は,Major Axis Regression (MA) と呼ばれるものです。訳としては「主成分回帰」とされることが多いと思います。
類似のものに,Reduces Major Axis Regression (RMA) というものもあります。
http://aoki2.si.gunma-u.ac.jp/R/MA.html
http://aoki2.si.gunma-u.ac.jp/R/RMA.html
本記事の概要
よく用いられる近似の手法として、最小二乗法があります。
簡単に言えば、XY平面上の適当なプロットに対して、近似される関数を求める手法になります。
(以下、すべて1次関数を用いて近似することにします。)
しかし、一般的な最小二乗法では、XかYどちらか一方のデータにのみ誤差が含まれるという仮定があります。
例えば、「Xは誤差を含まず、Yに誤差が含まれており、各点とY軸方向の距離が最小になる1次関数を求める」 というケースが多いでしょう。
それでは、XとYいずれのデータにも誤差が含まれる場合にはどうすれば良いのでしょうか?
ここで最小距離二乗法が1つの答えとなります。
「各点と、X軸方向とY軸方向の両方の距離(すなわち点と直線の距離)が最小になる1次関数を求める」ことができるように、最小二乗法を拡張したものが、最小距離二乗法になります。
これが,「主成分回帰」と言われる所以です。
最小二乗法とは
最小二乗法とは?(Wikipedia)
一般的な最小二乗法においては、Y軸の値に誤差が含まれます。
例えば、X軸は時間や個数、人数などであり、Y軸は測定値であることが多いでしょう。
したがって、最小二乗法では、各点と1次関数のY軸方向の距離を最小化する1次関数を見つけます。
それでは、前章の最小二乗法の例について、MATLABを使って実践してみます。
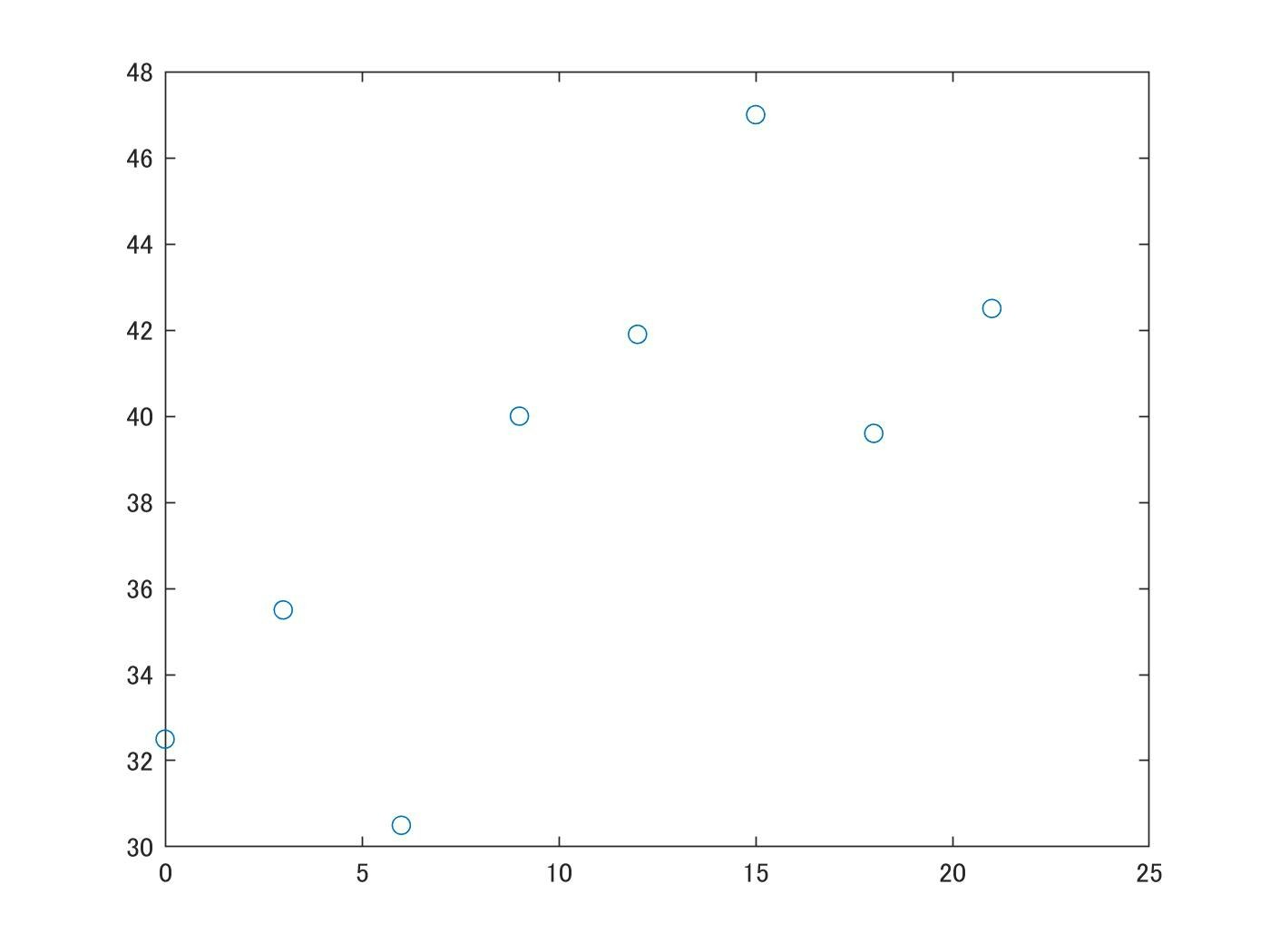
まずは、適当なプロットを用意します。今回は以下のような8個の点を用意します。
x = [0 3 6 9 12 15 18 21]';
y = [32.5 35.5 30.5 40 41.9 47 39.6 42.5]';
plot(x, y, 'o');
次に、以下のような処理を施し、目標の1次関数の傾き$u(1)$とY切片$u(2)$を算出します。
A = ones(8,2);
A(:, 1) = x;
v = y;
u = inv(A'*A)*A'*v;
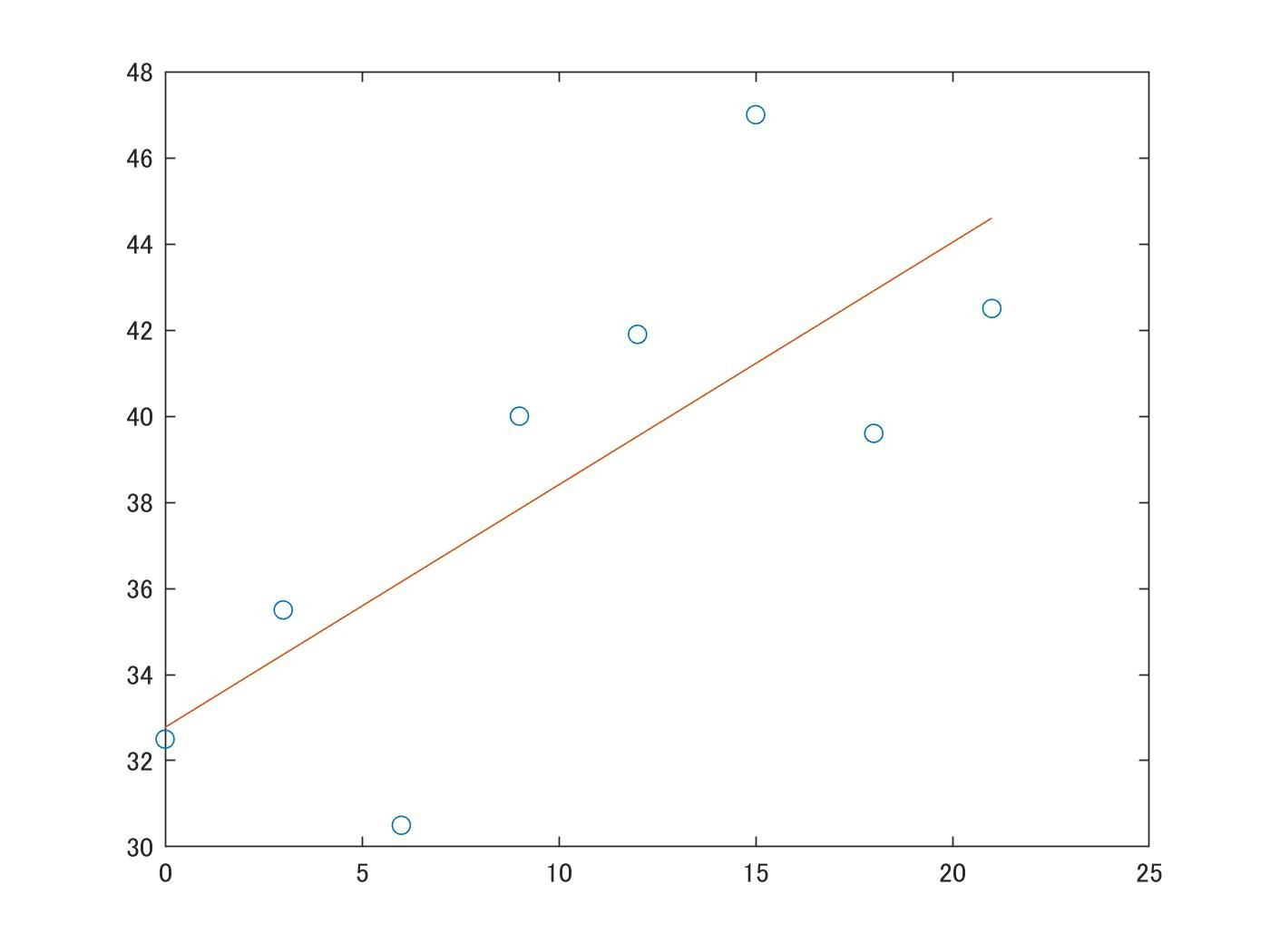
x2 = 0:21; %目標の1次関数のx軸範囲が、用意したxの0~21までであることを示す
y2 = u(1) .* x2 + u(2);
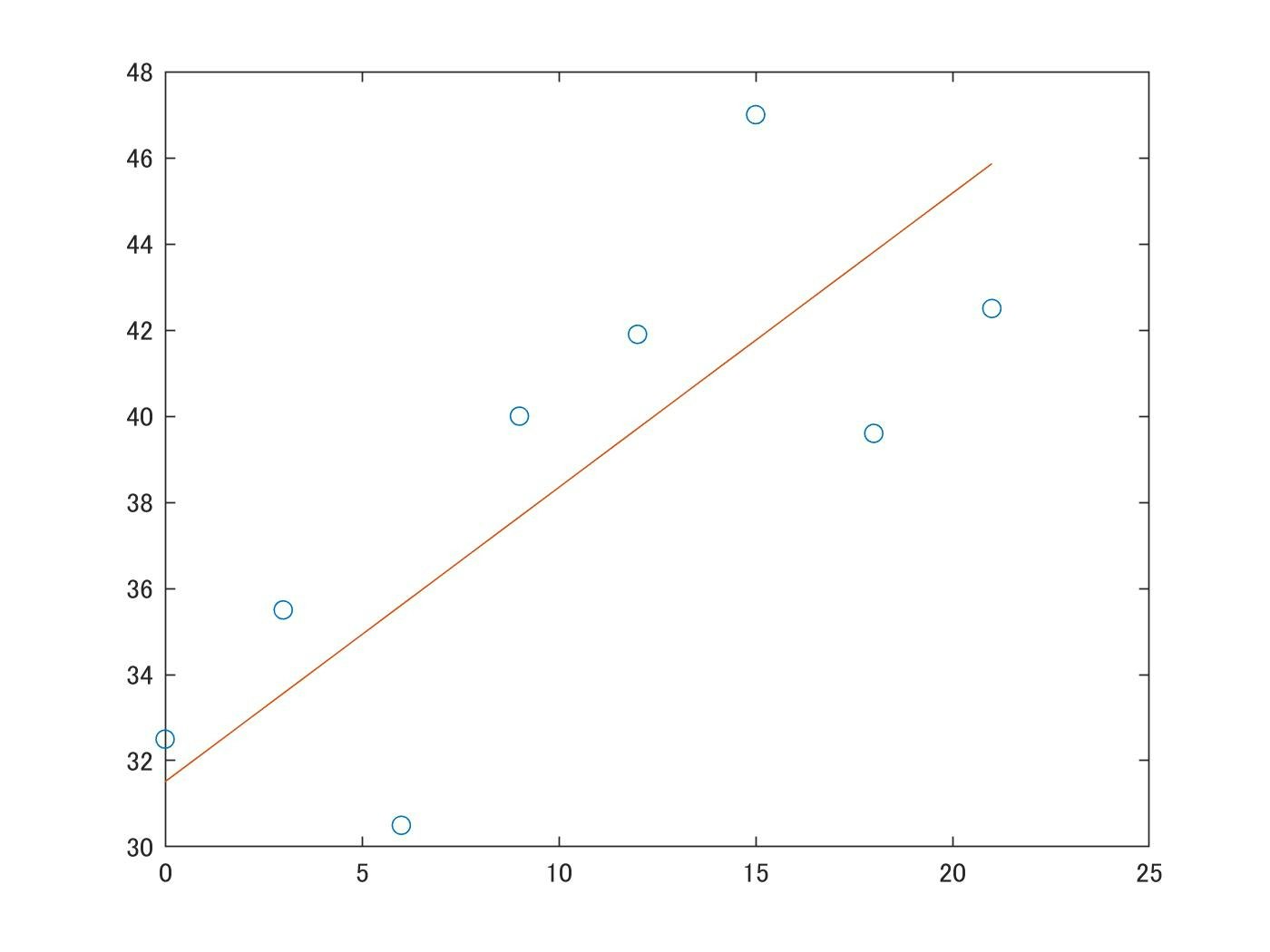
plot(x2, y2)
できました。
最小“距離”ニ乗法とは
さて、最小距離ニ乗法では、Y軸の値のみならず、X軸の値に含まれる誤差も考慮します。
X軸も、Y軸も測定値であると考えれば良いでしょう。
(余談:ちなみに筆者は、センサから推定される歩行者の連続した位置情報から、進行方向を算出するために本手法を検討しました。)
したがって、最小距離二乗法では、各点と1次関数の距離を最小化する1次関数を見つけます。
本章では、はじめに最小距離二乗法の解の導出について考えてみます。
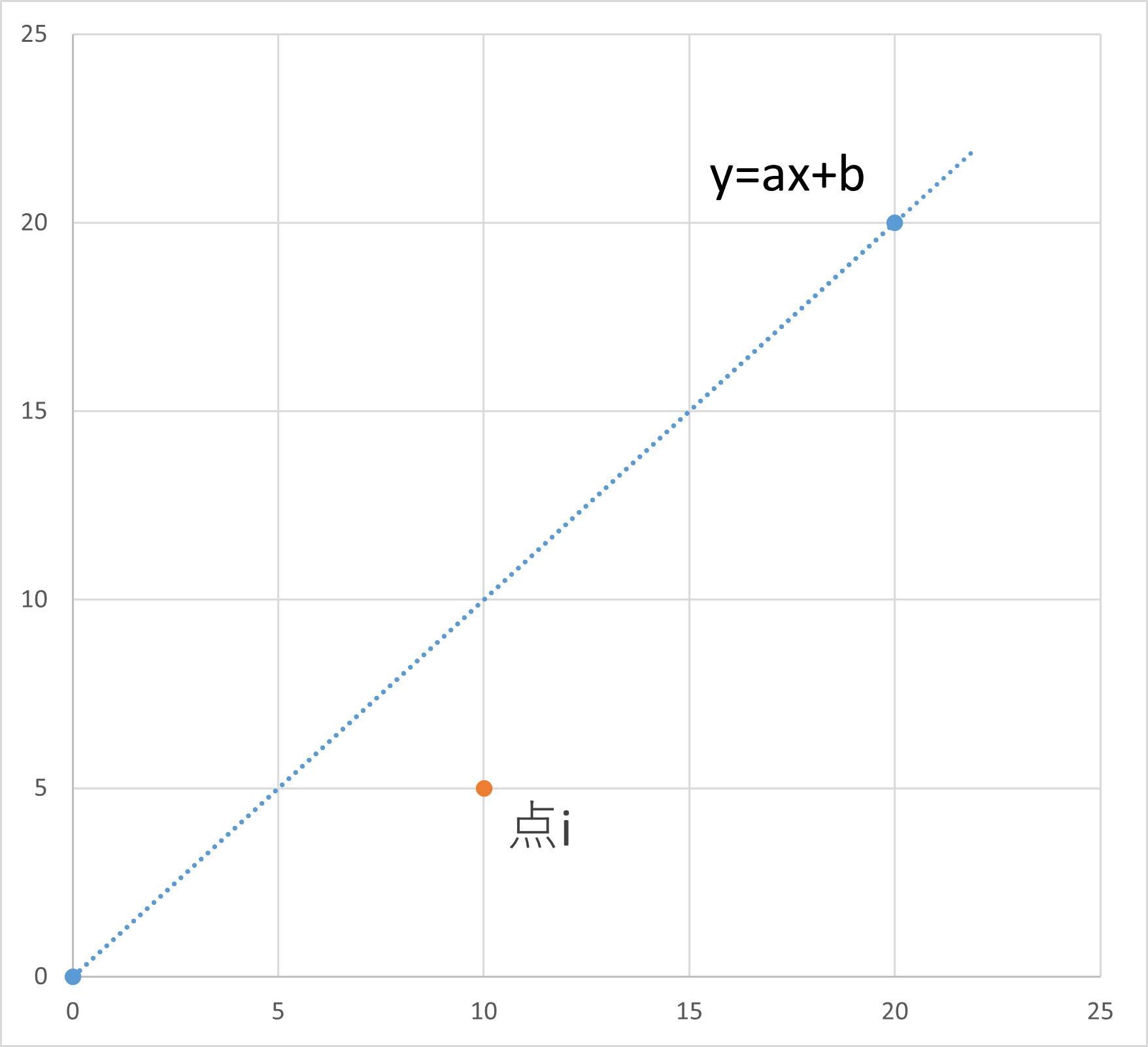
以下の図のように、点i $(x_i, y_i)$ (ただし、$i$は自然数で、$0<i\leq n$ を満たす) と
$y=ax+b$ の直線を考えます。
(一般的な場合を考えますので、今回は目盛りは無視してください。)
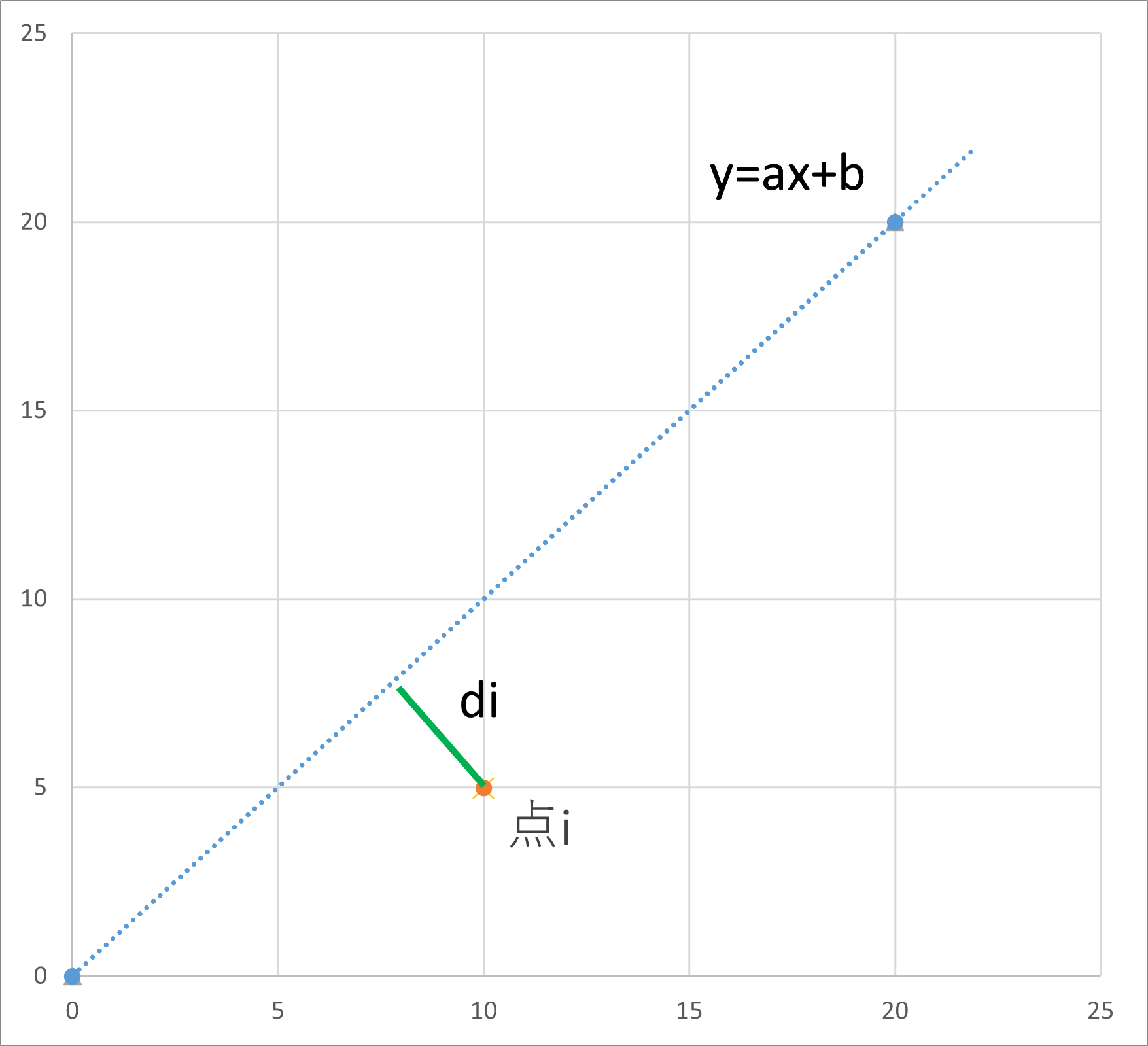
次に、点$i$から直線 $y=ax+b$ に向けて垂線を下ろし、距離$d_i$を求めます。
この計算は$d_i$と$y=ax+b$が直交していることを利用すると導出することができます。
$\displaystyle {d_i}^2 = \frac{1}{1+a^2} (y_i-ax_i-b)^2$ $- (1)$
さて、点の数は$n$個ありますから、
最小化したい値は、$n$個の点と直線の距離の2乗の総和になります。
この総和を$D$とすると、
$D = \displaystyle \Sigma{d_i}^2 = \Sigma{\frac{1}{1+a^2} (y_i-ax_i-b)^2}$ $-(2)$
$a$と$b$を変数とみなすと、$D$を最小にするためには以下を満たす必要があります。
$\displaystyle \frac{\Delta{D}}{\Delta{a}} = 0, \frac{\Delta{D}}{\Delta{b}} = 0$ $-(3)$
式(3)を$a$について解くと、
$I^2a+Ka-I = 0$ $-(4)$
$a = \displaystyle \frac{1}{2I}(-K\pm\sqrt{K^2+4I^2})$ $-(5)$
ただし、
$I = (\Sigma{x_i})(\Sigma{y_i}) - n\Sigma{x_i}{y_i} = n^2(\bar{x} \bar{y} - \bar{xy})$ $-(6)$
$K = n(\Sigma{y_i}^2 - \Sigma{x_i}^2) + (\Sigma{x_i})^2 - (\Sigma{y_i})^2 = n^2(\bar{y^2} - \bar{x^2} + \bar{x}^2 - \bar{y}^2)$ $-(7)$
また$b$については以下の通り。
$b = \displaystyle \frac{1}{n}(\Sigma{y_i} - a\Sigma{x_i}) = \bar{y} - a\bar{x}$
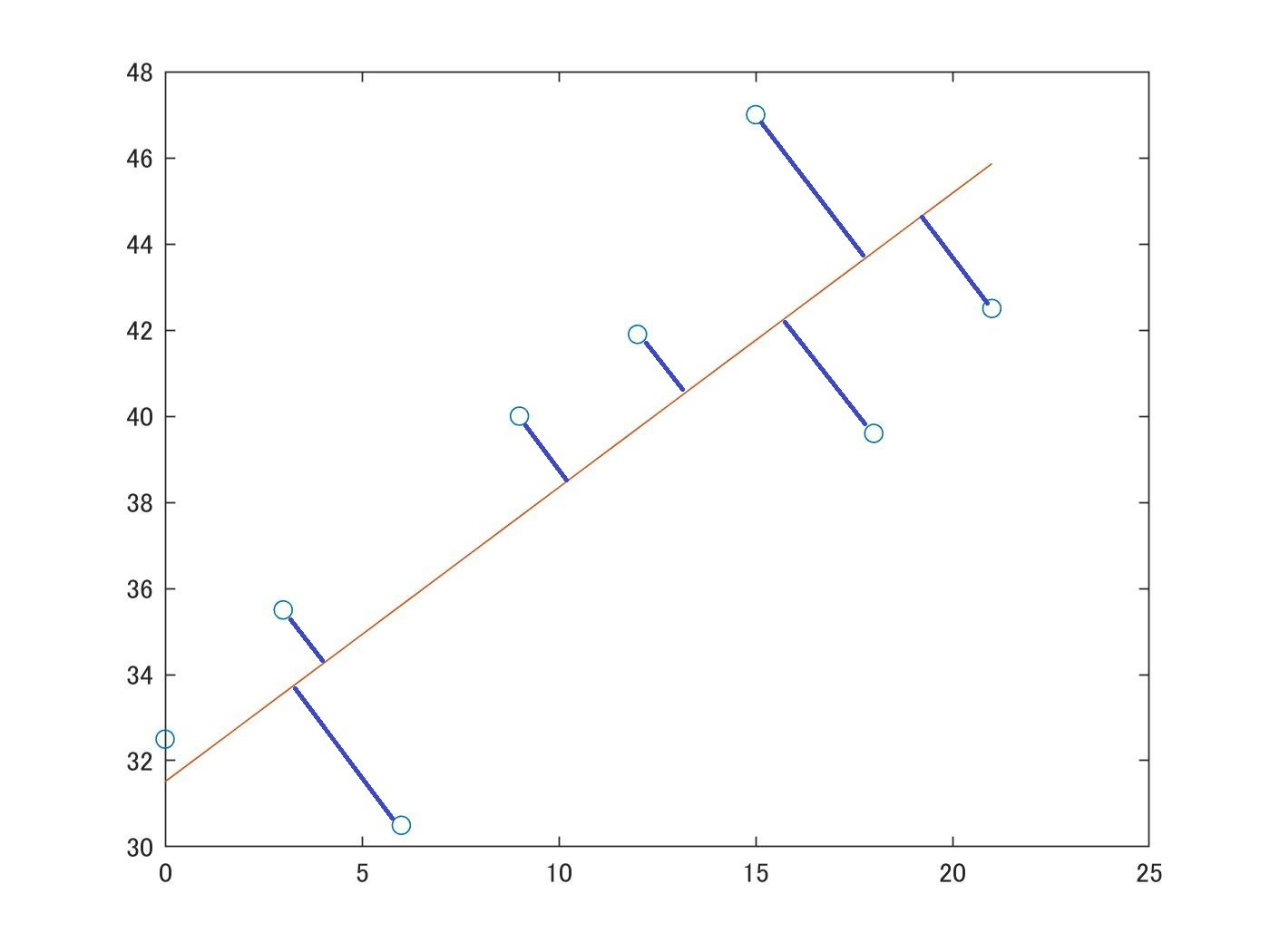
以上の計算を実装すれば、入力のプロットに対して、自動的にそれらの近似直線を出力することができます。
それでは、前々章の最小距離二乗法の例について、MATLABを使って実践してみます。
まずは、最小二乗法の実装と同様の8個の点を用意します。(コードおよび図は割愛)
次に、以下のような処理を施し、目標の1次関数$\space y = a \times x + b$の傾き$\space a$とY切片$\space b$を算出します。
n=8; % プロット数
avr_x = mean(x);
avr_y = mean(y);
d = dot(x,y);
avr_d = d/n;
avr_xx = dot(x,x)/n;
avr_yy = dot(y,y)/n;
avr_x2 = avr_x.^2;
avr_y2 = avr_y .^2;
% 計算式の簡略化のために置く
I = (n.^2) .* (avr_x.*avr_y - avr_d);
K = n.^2 .* (avr_yy - avr_xx + avr_x2 - avr_y2);
a = (-K - sqrt(K.^2 + 4.*(I.^2))) / (2.*I);
b = avr_y - a .* avr_x;
% (a, b) = (0.6833767859339025, 31.512043747694022)
x3 = 0:21;
y3 = a .* x3 + b;
plot(x3, y3)
できました。
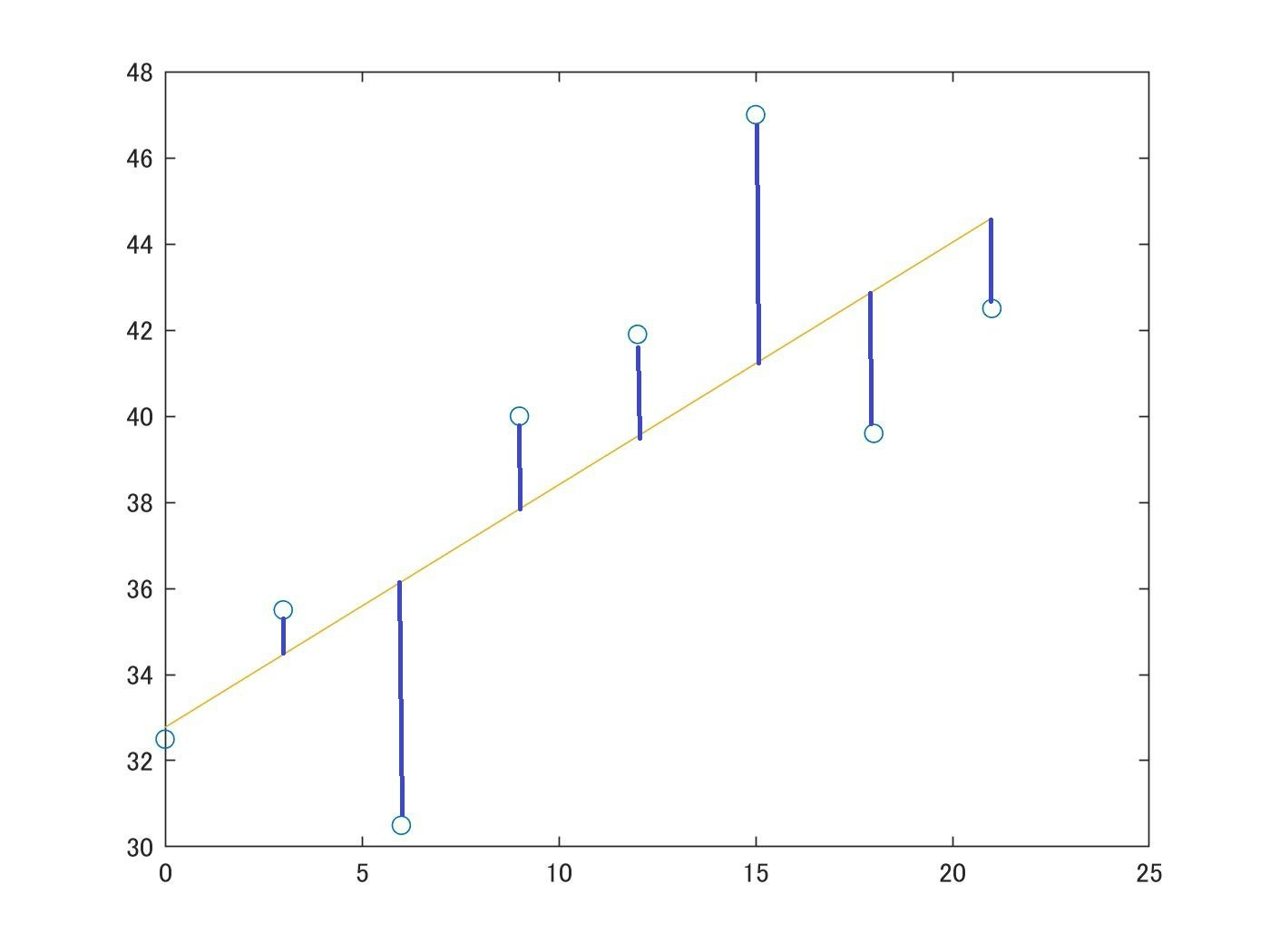
最後に、両方の出力結果を比較してみましょう。
下図の黄色線が最小距離二乗法によって求められた1次関数で、
赤線色が最小二乗法によって求められた1次関数になります。
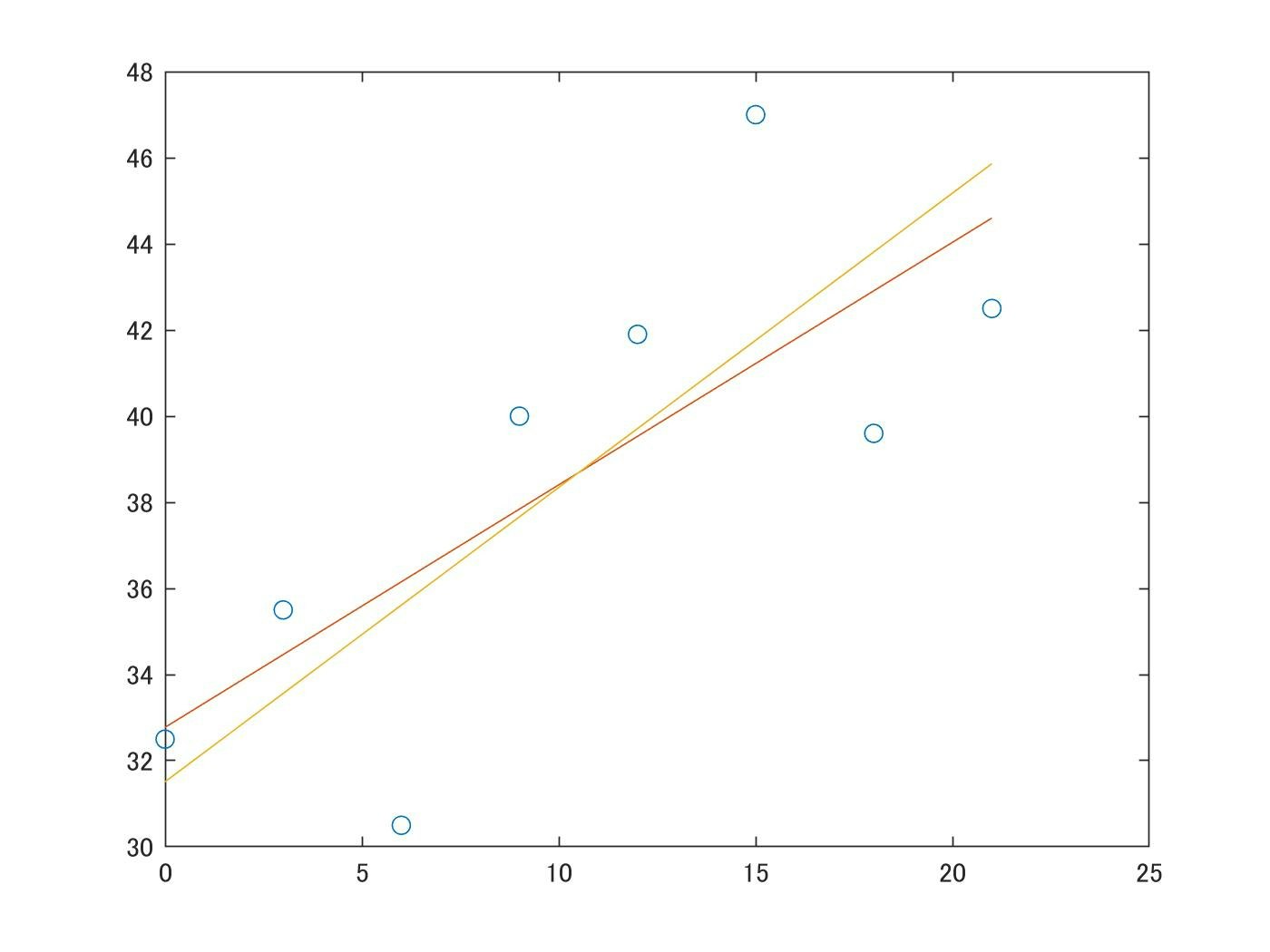
さすがに目視では定性的な違いはわかりませんが、
8個程度のデータでも、計算方法によって異なるグラフが出力されることがわかります。
おわりに
今回は、最小二乗法の拡張として、通称“最小距離二乗法”を紹介しました。
データのX軸とY軸の両方に誤差が含まれる場合に、それらのプロットを1次関数を用いて近似したいときに有効です。