文字列系 stoi stack 累積和modなど

stoiは文字列を数値に変換する

stoi(s.substr(0, cnt));

こんな感じで使う

//カッコ列の整合性に関する問題は超定番の判定方法がある
//stackを用意する
//左カッコが来たらstackに追加
//右カッコがきたときstackが空だったらエラー検出で空じゃなかったらstackにある左カッコと
//今ある右カッコとをペアにしてstackからpopする
例題
ドワンゴからの挑戦状　2525文字列分解

int main() {
	string s; cin >> s;
	stack<int>st;
	int cnt2 = 0;
	int cnt5 = 0;
	int ans = 0;
	for (int i = 0; i < s.size(); ++i) {
		if (s[i] == '2') {
			cnt2++;
		}
		else {
			cnt5++;
		}
		ans = max(ans,cnt2 - cnt5);
		if (st.empty()) {
			if (s[i] == '2')st.push(2);
			else {
				cout << -1 << endl;
				return 0;
			}
		}
		else {
			if (s[i] == '5') {
				st.pop();
			}
			else {
				st.push(2);
			}
		}
	}
	if (!st.empty()) {
		cout << -1 << endl;
	}
	else {
		cout << ans << endl;
	}
	return 0;
}

agc 005 Aなども

# include<iostream>
# include<vector>
# include<algorithm>
# include<string>
# include<map>
# include<math.h>
# include<queue>
# include<deque>
# include<stack>
# include<cstdio>
# include<utility>
# include<set>
# include<list>
# include<cmath>
# include<stdio.h>
# include<string.h>
# include<iomanip>
# include<cstdio>
# include<cstdlib>
# include<cstring>
using namespace std;
# define FOR(i, a, b) for (ll i = (a); i <= (b); i++)
# define REP(i, n) FOR(i, 0, n - 1)
# define NREP(i, n) FOR(i, 1, n)
using ll = long long;
using pii = pair<int, int>;
using piii = pair<pii, pii>;
const ll dx[4] = { -1, 0, 0, 1 };
const ll dy[4] = { 0, -1, 1, 0 };
const ll INF = 1e9 + 7;
const ll inf = 1LL << 50;
int gcd(int x, int y) {
	if (x < y)swap(x, y);
	if (y == 0)return x;
	return gcd(y, x%y);
}
void mul(ll a, ll b) {
	a = a * b % INF;
}
struct Accelerate_Cin {
	Accelerate_Cin() {
		cin.tie(0);
		ios::sync_with_stdio(0);
		cout << fixed << setprecision(20);
	};
};
///////////////////////////////////////

//頂点数n(1<=n<=18)
//1から出発してnまで移動するようなパスですべての頂点をちょうど一度だけ通るようなものは何通りか
//best[S+{j}][j]=best[S][i]+w[i][j]
//best[S][i]はSのすべての頂点を経由してiに到達したときの最小重みパス
int n;
int ans = 0;
bool visited[20];
int a[20][20];
vector<int>G[20];
bool dp[20][1<<18]
void dfs(int N,int cnt) {
	dp[N]
	if (visited[N])return;
	visited[N] = true;
	if (N == n - 1 && cnt == n - 1) {
		ans++;
		ans %= INF;
	}
	for (int a : G[N]) {
		dfs(a, cnt + 1);
	}
	visited[N] = false;
	return;
}
int main() {
	cin >> n;
	REP(i, n)visited[i] = false;
	REP(i, n) {
		REP(j, 1 << 18) {
			dp[i][j] = false;
		}
	}
	REP(i, n) {
		REP(j, n) {
			cin >> a[i][j];
			if (a[i][j] > 0) {
				G[i].push_back(j);
				G[j].push_back(i);
			}
		}
	}
	dfs(0,0);
	cout << ans << endl;
	//dp[S][i]:=1から始まるパスでSの頂点をすべてちょうど一度通り最後にiにいるものの総数
	return 0;
}

z-アルゴリズム
文字列が与えられた時各iについてSとS[i:|S|-1]の最長共通接尾辞の長さを記録した配列Aを構築するアルゴリズム

aaabaaaab
921034210

こんな感じ
コードは以下

A[0] = S.size();
int i = 1, j = 0;
while (i < S.size()) {
  while (i+j < S.size() && S[j] == S[i+j]) ++j;
  A[i] = j;
  if (j == 0) { ++i; continue;}
  int k = 1;
  while (i+k < S.size() && k+A[k] < j) A[i+k] = A[k], ++k;
  i += k; j -= k;
}

int c = 0;
for (int i = 1; i < S.size(); i++){
  if (i+A[i-c] < c+A[c]) {
    A[i] = A[i-c];
  } else {
    int j = max(0, c+A[c]-i);
    while (i+j < S.size() && S[j] == S[i+j]) ++j;
    A[i] = j;
  }
}
A[0] = S.size();

方針が違うだけでほぼ同じコード

ライブラリにすると

vector<int> Zalgo(const string &S) {
    int N = (int)S.size();
    vector<int> res(N);
    res[0] = N;
    int i = 1, j = 0;
    while (i < N) {
        while (i+j < N && S[j] == S[i+j]) ++j;
        res[i] = j;
        if (j == 0) {++i; continue;}
        int k = 1;
        while (i+k < N && k+res[k] < j) res[i+k] = res[k], ++k;
        i += k, j -= k;
    }
    return res;
}

例題　who says a pun?

vector<int> Zalgo(const string &S) {
	int N = (int)S.size();
	vector<int> res(N);
	res[0] = N;
	int i = 1, j = 0;
	while (i < N) {
		while (i + j < N && S[j] == S[i + j]) ++j;
		res[i] = j;
		if (j == 0) { ++i; continue; }
		int k = 1;
		while (i + k < N && k + res[k] < j) res[i + k] = res[k], ++k;
		i += k, j -= k;
	}
	return res;
}

int main() {
	int N;
	string S;
	cin >> N >> S;
	int res = 0;
	for (int i = 0; i < N; ++i) {
		string T = S.substr(i);
		auto lcp = Zalgo(T);
		for (int j = 0; j < T.size(); ++j) {
			int l = min(lcp[j], j);
			res = max(res, l);
		}
	}
	cout << res << endl;
	return 0;
}

abc 164 E

# include<iostream>
# include<cassert>
# include<cctype>
# include<cerrno>
# include<cfloat>
# include<vector>
# include<algorithm>
# include<string>
# include<map>
# include<math.h>
# include<queue>
# include<deque>
# include<stack>
# include<cstdio>
# include<utility>
# include<set>
# include<list>
# include<cmath>
# include<stdio.h>
# include<string.h>
# include<iomanip>
# include<cstdio>
# include<cstdlib>
# include<cstring>
# include<bitset>
# include<functional>
# include<iterator>
# include<complex>
# include<fstream>
# include<random>
# include<ctype.h>
# include<stdio.h>
using namespace std;
# define FOR(i, a, b) for (int i = (a); i <= (b); i++)
# define REP(i, n) FOR(i, 0, n - 1)
# define NREP(i, n) FOR(i, 1, n)
using ll = long long;
using pii = pair<int, int>;
using PII = pair<ll, ll>;
using piii = pair<pii, pii>;
using Pi = pair<int, pii>;
using Graph = vector<vector<int>>;
const int dx[4] = { 0, -1, 1, 0 };
const int dy[4] = { -1, 0, 0, 1 };
bool check(int x, int y) {
	if (0 <= x && x<55 && 0 <= y && y<55)return true;
	else return false;
}
const ll INF = 1e+7;
int gcd(int x, int y) {
	if (x < y)swap(x, y);
	if (y == 0)return x;
	return gcd(y, x%y);
}
void mul(ll a, ll b) {
	a = a * b % INF;
}
using Graph = vector<vector<int>>;

long long modinv(long long a, long long m) {
	long long b = m, u = 1, v = 0;
	while (b) {
		long long t = a / b;
		a -= t * b; swap(a, b);
		u -= t * v; swap(u, v);
	}
	u %= m;
	if (u < 0) u += m;
	return u;
}
const double PI = 3.14159265358979323846;
const int MAX = 510000;
ll fac[MAX], finv[MAX], inv[MAX];
//テーブルをつくる前処理
void COMinit() {
	fac[0] = fac[1] = 1;
	finv[0] = finv[1] = 1;
	inv[1] = 1;//mod pにおける1,2,,,nの逆元
	for (int i = 2; i < MAX; ++i) {
		fac[i] = fac[i - 1] * i%INF;
		inv[i] = INF - inv[INF%i] * (INF / i) % INF;
		finv[i] = finv[i - 1] * inv[i] % INF;
	}
}

ll COM(int n, int k) {
	if (n < k)return 0;
	if (n < 0 || k < 0)return 0;
	return fac[n] * (finv[k] * finv[n - k] % INF) % INF;
}
double Euclidean_distance(double x1, double y1, double x2, double y2) {
	return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}

int prime[1001000];//i番目の素数
bool is_prime[1001010];//is_prime[i]がtrueならiは素数
					   //n以下の素数の数を返す
int sieve(int n) {
	int p = 0;
	for (int i = 0; i <= n; ++i) {
		is_prime[i] = true;
	}
	is_prime[0] = false;
	is_prime[1] = false;
	for (int i = 2; i <= n; ++i) {
		if (is_prime[i]) {
			prime[p] = i;
			p++;
			for (int j = 2 * i; j <= n; j += i) {
				is_prime[j] = false;
			}
		}
	}
	return p;
}

//素因数分解
map<int, int>prime_factor(int n) {
	map<int, int>res;
	for (int i = 2; i*i <= n; ++i) {
		while (n%i == 0) {
			++res[i];
			n /= i;
		}
	}
	if (n != 1)res[n] = 1;
	return res;
}

const ll MOD = 2019;
ll powmod(ll a, ll k) {
	ll ap = a, ans = 1;
	while (k) {
		if (k & 1) {
			ans *= ap;
			ans %= MOD;
		}
		ap = ap * ap;
		ap %= MOD;
		k >>= 1;
	}
	return ans;
}
ll invi(ll a) {
	return powmod(a, MOD - 2);
}
//逆元Aを足したときのmodで割った余りは
//+=invi(A)
///////////////////////////////////////

//Sについて下からi桁目の数字をSiと表記するまたSの文字列の長さをNとする
//加えてxを2019で割った余りをx%2019と表記する
//sについて桁ごとに分解して表現してみると
//S1*1+S2*10+S3*100+,,,,,,+SN*10~(N-1)となる
//S%2019は(S1*1%2019+S2*10%2019+,,,+SN*10^(N-1)%2019)%2019
//一般化するとΣ(Si*10^(i-1)%2019)%2019(1<=i<=N)
//ここでsum[k]=ΣSi*10^(i-1)%2019)%2019(1<=i<=K)と定義すると
//sum[0]=0,sum[k]=(sum[k-1]+(Sk*10^(k-1)%2019)%2019と
//10^k%2019=(10^(k-1)%2019)%2019の二つを組み合わせ累積和のようにして解くことができる
//ここでSのi桁目からj桁目までを取り出した数はこれをPとして
//P=(ΣSk*10^(k-1)(1<=k<=j)-ΣSk*10^(k-1)(1<=k<=i-1))/10^(i-1)
//2019は互いに素なので上記の分子が2019の倍数になっていればよく
//これをさらに変形するとΣ(Sk*10^(k-1)%2019)%2019(1<=k<=j)
//Σ(Sk*10^(k-1)%2019)%2019(1<=k<=i-1)となるi,jのペアを探せばよいことがわかる
//この式は先ほど作成したsum[k]そのものでsum[i-1]=sum[j]
//となるi,jのペアを探せばよい
//cnt[k]:sum[x]=kとなるようなxの個数という配列を用意しておき
//1,sum[i]を計算
//2,cnt[sum[i]]を答えに加算
//3,cnt[sum[i]]]++という操作をi=0から繰り返していけばよい
ll sum[200020];
ll cnt[2020];
int main(){
	string S; cin >> S;
	reverse(S.begin(), S.end());
	ll n = S.size();
	ll ans = 0;
	REP(i, 200020)sum[i] = 0;
	REP(i, 2020)cnt[i] = 0;
	cnt[0] = 1;
	for (ll i = 1; i <= n; ++i) {
		sum[i] = (sum[i - 1] + (S[i - 1] - '0')*powmod(10, i - 1)) % 2019;
		ans += cnt[sum[i]];
		cnt[sum[i]]++;
	}
	cout << ans << endl;
	return 0;
}

類題
abc158 E
2のときと5の時は例外処理が必要だがそれ以外は同じ

int main(){
	int N, P; cin >> N >> P;
	string S; cin >> S;
	reverse(S.begin(), S.end());
	if (P == 2) {
		ll ans = 0;
		REP(i, N) {
			if ((S[i] - '0') % 2 == 0) {
				ans += (N - i);
			}
		}
		cout << ans << endl;
	}
	else if (P == 5) {
		ll ans = 0;
		REP(i, N) {
			if ((S[i] - '0') % 5 == 0) {
				ans += (N - i);
			}
		}
		cout << ans << endl;
	}
	else {
		ll sum[200020];
		ll cnt[10010];
		REP(i, 10010)cnt[i] = 0;
		sum[0] = 0;
		cnt[0] = 1;
		ll ans = 0;
		for (int i = 1; i <= N; ++i) {
			sum[i] = (sum[i - 1] + ((S[i - 1] - '0')*powmod(10, i - 1, P)) % P) % P;
			ans += cnt[sum[i]];
			cnt[sum[i]]++;
		}
		cout << ans << endl;
	}
	return 0;
}

zerosumranges

ll A[200010];
ll sum[200020];
int main(){
	int N; cin >> N;
	REP(i, N)cin >> A[i];
	sum[0] = 0;
	for (int i = 1; i <= N; ++i) {
		sum[i] = sum[i - 1] + A[i - 1];
	}
	vector<ll>v;
	for (int i = 0; i <= N; ++i) {
		v.push_back(sum[i]);
	}
	sort(v.begin(), v.end());
	ll ans = 0;
	for (int i = 0; i <= N;) {
		ll cnt = 1;
		while (v[i] == v[i + 1]) {
			cnt++;
			i++;
			if (i == N)break;
		}
		ans += (cnt * (cnt - 1)) / 2;
		i++;
		if (i == N)break;
	}
	cout << ans << endl;
	return 0;
}

rem of sum is num
A[i]を全て1引いておく、mapやqueueで状態を管理するなどのテクニックが必要だが大まかには同じ

ll A[200020];
ll sum[200010];
int main(){
	ll N, K; cin >> N >> K;
	REP(i, N) {
		cin >> A[i];
		A[i]--;
	}	
	sum[0] = 0;
	REP(i, N) {
		sum[i + 1] = (sum[i] + A[i]) % K;
	}
	map<int,int>mp;
	queue<int>que;
	ll ans = 0;
	REP(i, N+1) {
		ans += mp[sum[i]];
		mp[sum[i]]++;
		que.push(sum[i]);
		if (que.size() == K) {
			mp[que.front()]--;
			que.pop();
		}
	}
	cout << ans << endl;
	return 0;
}

abc141 E ローリングハッシュ＋二分探索/z-algorithm
二分探索＋ローリングハッシュ
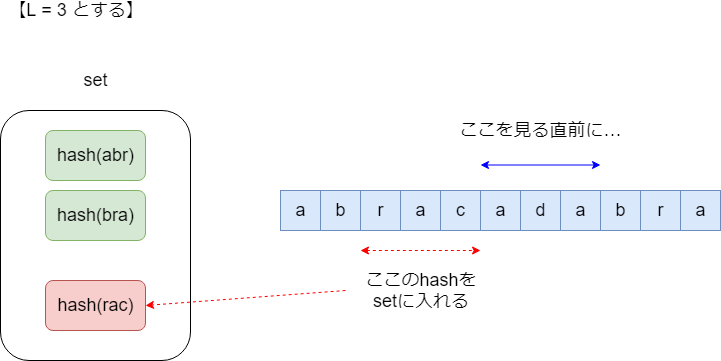
文字列Sの連続部分文字列として位置が重ならずに2回以上出現する、長さLの文字列が存在する、ということを長さLは条件を満たすと呼ぶことにする注目すべき性質としてもし長さLが条件を満たす場合必ずL-1も条件を満たします。単に長さLで条件を満たしている文字列の末尾を除いた文字列を考えればよいこの性質から二分探索ができるので長さLをある値に固定した時それは条件を満たすか？という判定問題が解ければよい判定問題を解くためにローリングハッシュというものを使う。これはある与えられた文字列についてその部分文字列の一致判定を大量に行いたい時に便利なアルゴリズムハッシュとは文字列などをある規則で整数に変換したもので2つの文字列をそれぞれ変換した整数が一致していれば文字列が一致したとみなす。与えられた文字列について前計算を行っておくことで部分文字列のハッシュをo(1)で計算しているのがローリングハッシュ固定したある長さLについて開始位置を一つずつずらしながら長さLの部分文字列のハッシュ値を求めていく。そして既に登場したハッシュ値をsetなどに入れておくことで同じハッシュ値が二回登場した時に検出することができるただし位置が重ならないという条件があるので求めたハッシュ値を即座にsetに入れてはいけない。今見ている値と重ならなくなったタイミング、具体的にはS.substr(i,L)を見る直前のタイミングでS.substr(i-L,L)のハッシュ値をsetに入れると良い。ここでS.substr(s,l)は開始位置s、長さlの部分文字列を表す