概要
つい先日、量子力学の輪読会がWebであって、そこで水素原子の電子軌道モデルを簡単に勉強できるツールを作りました。
ぴったり1ページに収まるので、量子力学以外の題材でも、学校の授業とかに使える感じです。
量子力学ゼミナール動画
※水素原子の電子軌道については、次の講義にアップされると思います
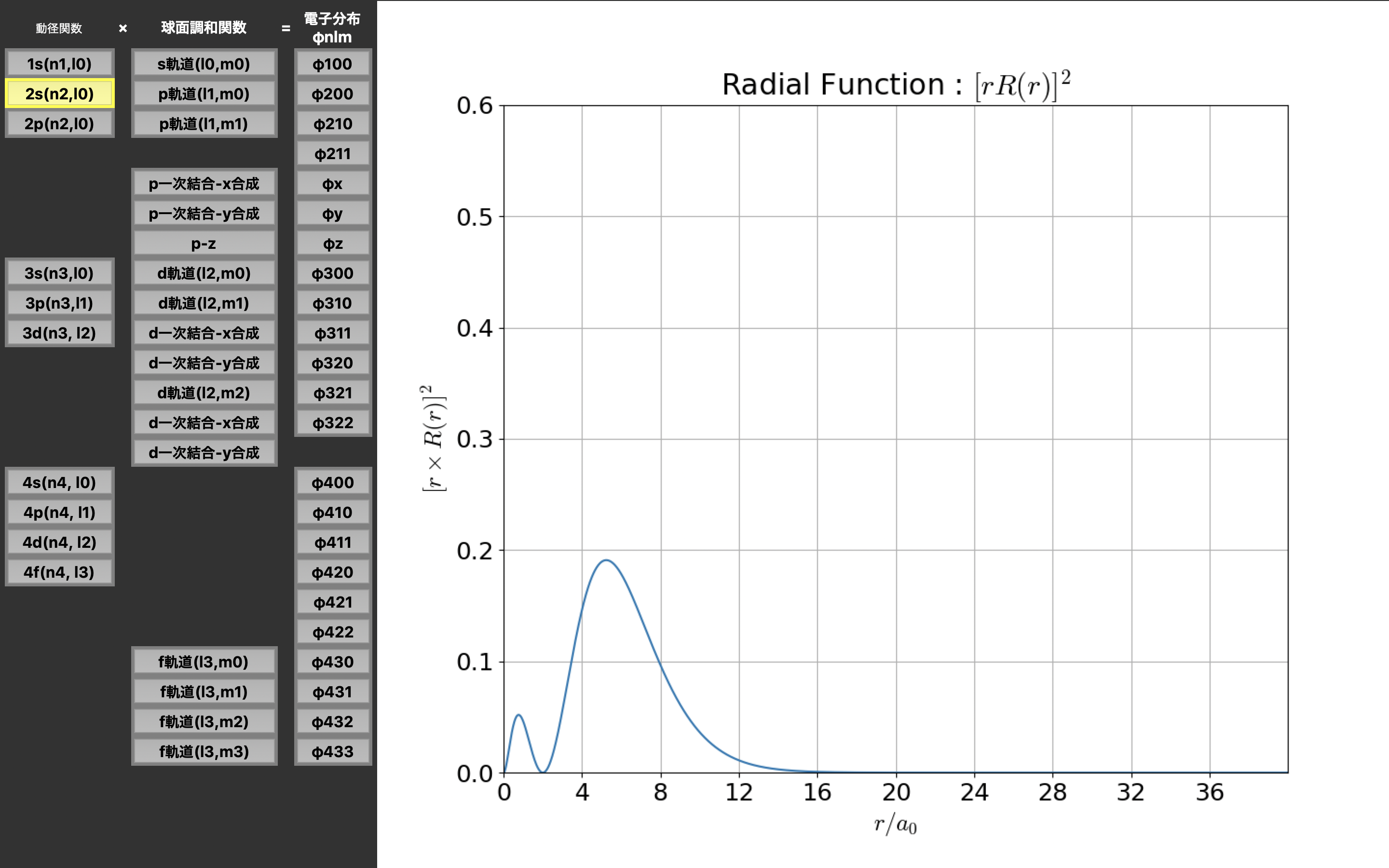
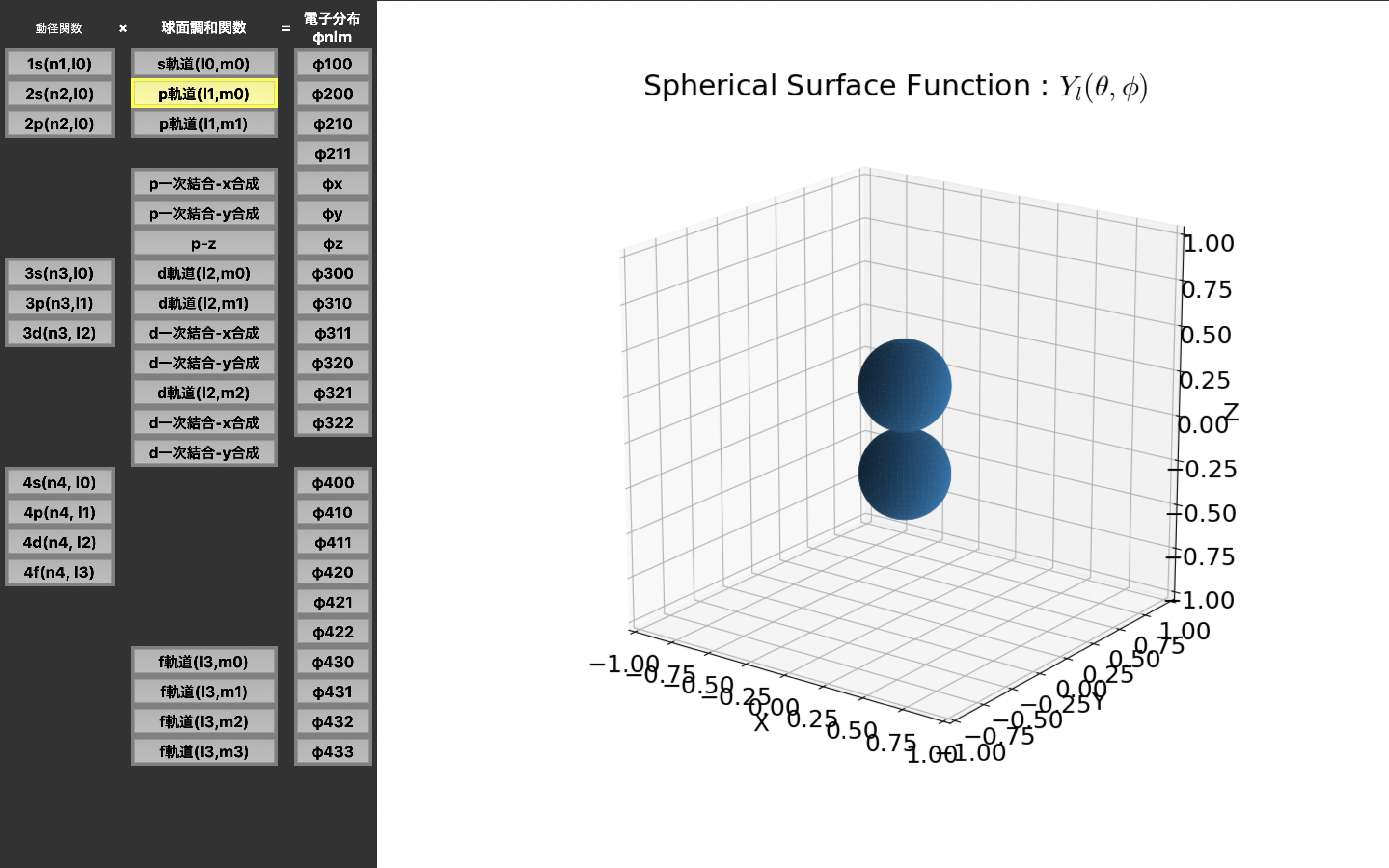
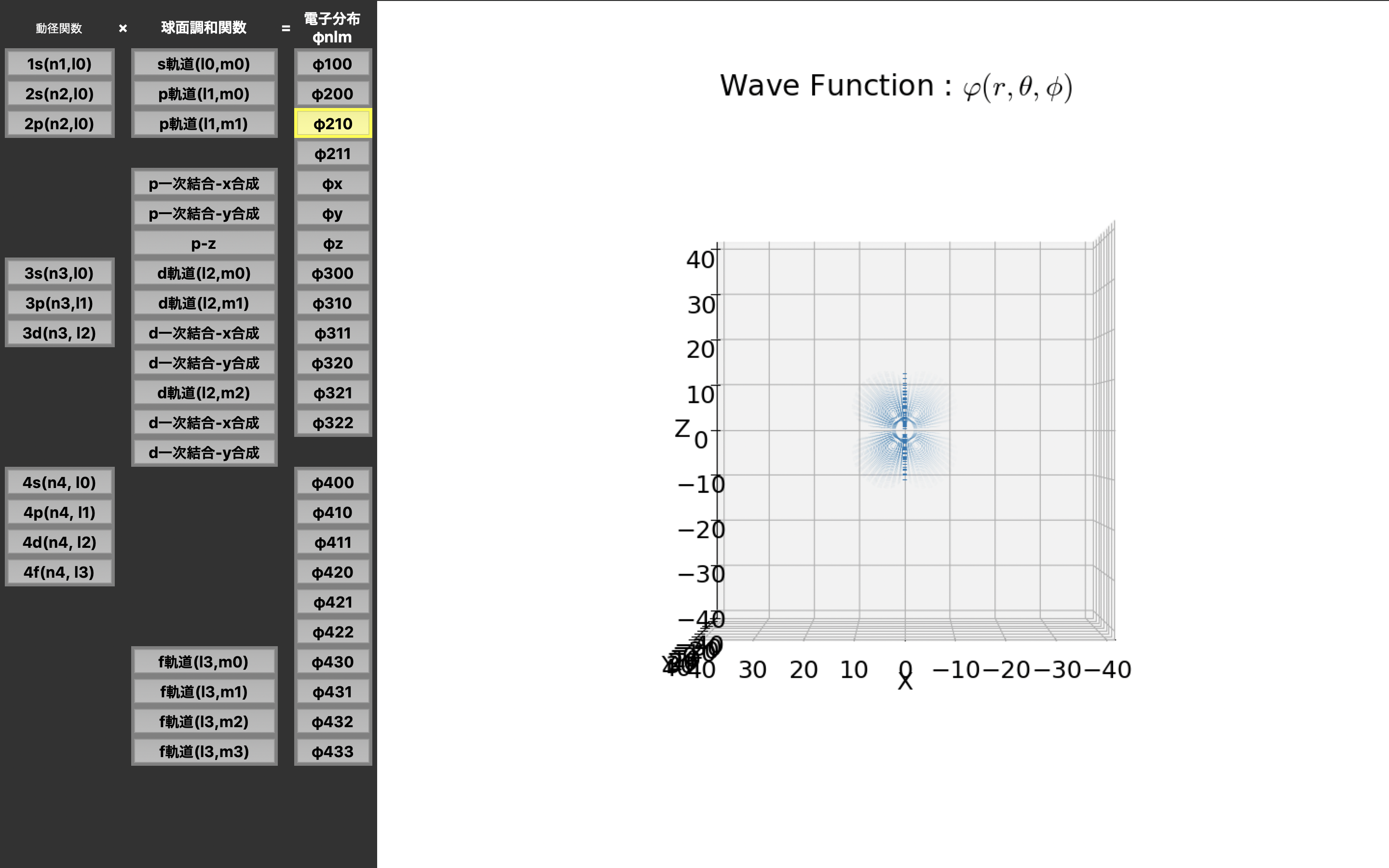
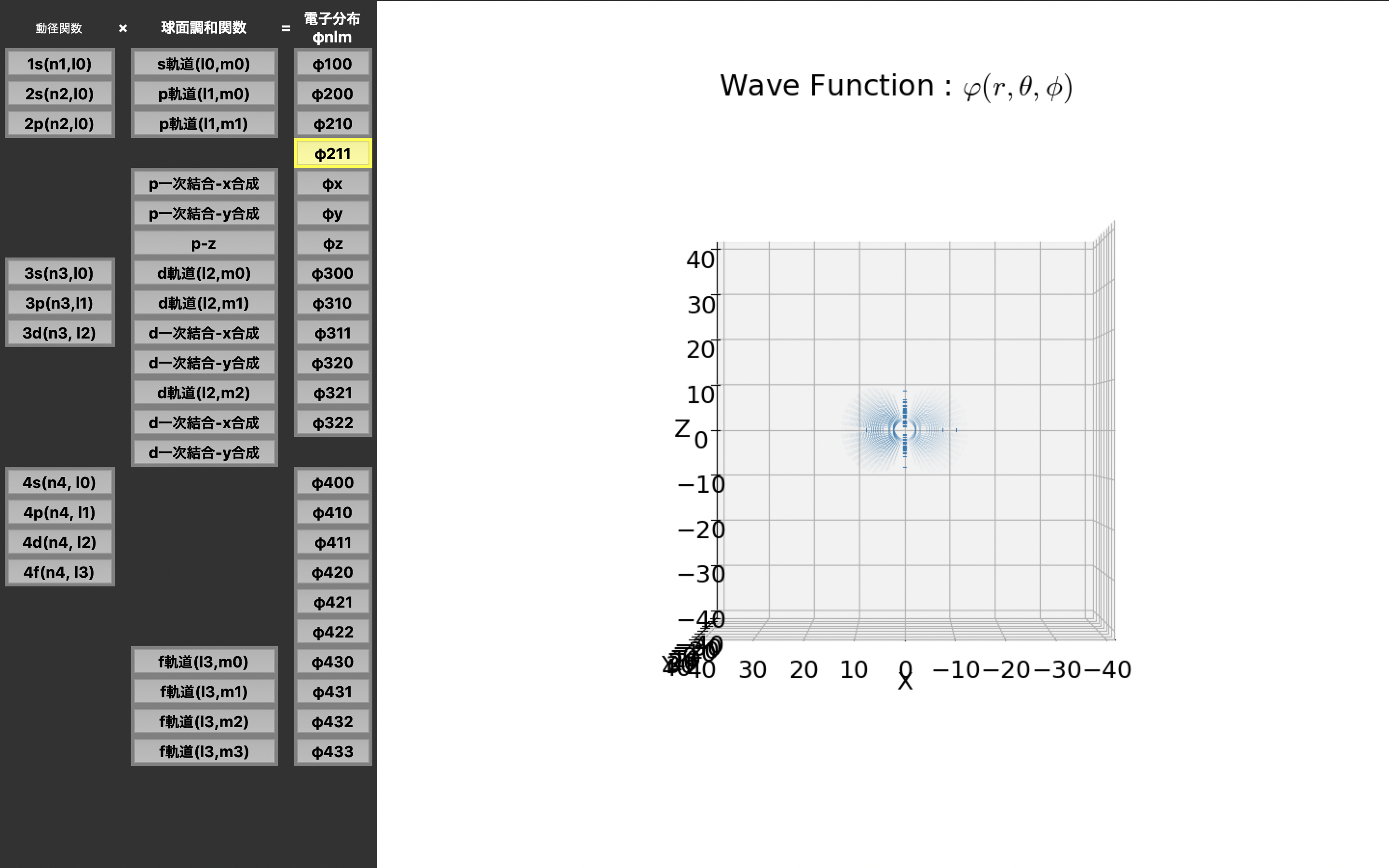
実行結果
想定している教科書
量子力学、量子化学を学んでいる方なら、おそらく認知度が高い教科書です。
-
小出昭一郎, "量子力学(I)", 裳華房(1990改訂版), pp98-103
-
ファインマン他、砂川重信訳、"ファインマン物理学V 量子力学", 岩波書店(1978)
画面
趣旨
私が大学の時に、量子化学や量子力学を勉強していたが、1原子系のモデルであっても軌道の形状が計算では直感的に分かりにくいものがあったので、作成した。
私の中では「電子分布$φ_{nlm}$」が結構面白くて、これはmatplotlibのquiverを使ってベクトル場を表現しているのだが・・・。
実は電子の分布が多ければ多いほどベクトル場の長さを微妙に長くしているので、こんなにはっきりと電子軌道を映せることで直感的なイメージが掴めたら・・・とか、量子化学に興味を持つ人が増えたらな・・・と思い作成しました。
実行環境
Mac OS Catalina 10.15.7
Python 3.7
Matplotlib 3.4.1
numpy 1.20.2
githubソースコード
汚くて、コメント少ないのはご容赦ください.
ただ、構造的には分かりやすい中身になっているはずなので、読めると思います。
修正・改善のご要望があれば、コメントをつけるなどして対応できますので、ご連絡ください。
自分で見たい方のために、以下にソースコードをちょっと概説したいと思います
プログラム
-
Selector.py : ボタンを選択、ボタンイベント関連。実行時のメインプログラム
-
Function.py : 2d plot, 3d plot
Selector.py
コードの8割くらいが、GUIの表示とボタンイベントの登録処理ですw
動径関数(球ベッセル関数)
def R_1s(self, r):
return 2 * np.exp(-r)
球面調和関数
def Y_0_0(self, theta, phi):
return 1 / np.sqrt(4 * np.pi)
計算の仕方
動径関数は$ r^2 \times R_{xx}(r)^2 $、
球面調和関数は$ {\rm Re} [Y_n^l(\theta, \phi)] $
電子軌道は$ |r^2 \times R_{xx}(r)^2 \times Y_n^l(\theta, \phi)|^2 $
を使って計算しています。
ボタンイベント
tk_btn = MarkerButton(self.parent_panel)
tk_btn["text"] = "s軌道(l0,m0)"
tk_btn["command"] = partial(self.press_for_graph, tk_btn, GraphView('3d',
lambda theta, phi: np.abs( self.Y_0_0(theta, phi) )))
tk_btn.grid(row=cnt, column=2, sticky=tk.W+tk.E+tk.N+tk.S)
tk_btn.configure(font=my_font)
ボタンイベントの中身はself.press_for_graph
def press_for_graph(self, sender, graph_func, graph_object=None):
self.select(sender)
if self._graph_object == None:
self._graph_object = SphericalSurface(self.master)
self._graph_object.plot(graph_func, graph_object)
plotの中身はFunction.pyの下の方に
class SphericalSurface(ttk.Frame):
def __init__(self, root):
super().__init__(root)
self.master = root
self._figure = plt.figure(figsize=(10,6))
self._canvas = FigureCanvasTkAgg(self._figure, master=root)
self._canvas.draw()
self._canvas.get_tk_widget().pack(side=tk.TOP, fill=tk.BOTH, expand=1)
self._toolbar = NavigationToolbarExt(self._canvas, self, self._figure)
self._axes_now = None
self.init_plot()
def init_plot(self):
plt.clf()
self._figure.clf()
ax = plt.subplot(111)
def plot(self, graph_func, fig_rule):
plt.clf()
self._axes_now = self._figure.add_subplot(111, projection='3d', title='Spherical Surface Function', xlabel='X', ylabel='Y', zlabel='Z')
self._figure.add_axes(self._axes_now)
graph_func.plot(self._axes_now, self._figure)
色々なグラフを条件で分けて表示
クラスGraphViewとして次のように書いてあります。
class GraphView:
def __init__(self, datatype, func, fig_rule=None):
self._datatype = datatype
self._func = func
self._fig_rule = fig_rule
def plot(self, axes, figure):
if self._datatype == '2d':
self.plot2d(axes, figure)
elif self._datatype == '3d':
self.plot3d(axes, figure)
elif self._datatype == '3d_field':
self.plot3d_field(axes, figure)
GraphViewというオブジェクトを生成して、それを渡すような形をとっています。
datatypeの中身によって、描かれるグラフが変わって、'2d', '3d', '3d_field'を選択して、funcの中に実際に描く関数を、fig_ruleに描画する時に特別な処理(z軸View, x軸Viewに移動など)を入れる場合に使用します。
フルスクリーン表示、画面表示
root = tk.Tk()
root.title("Spherical Surface Demonstration")
root.attributes('-fullscreen', True)
app = Application(master=root)
app.mainloop()
画面の中にmatplotlibを入れる
FigureCanvasTkAggを使用して実装します。
self._canvas = FigureCanvasTkAgg(self._figure, master=root)
self._canvas.draw()
self._canvas.get_tk_widget().pack(side=tk.TOP, fill=tk.BOTH, expand=1)