会社の案件で、理論的な背景があるのでまとめておく
モータを使って生地を巻く
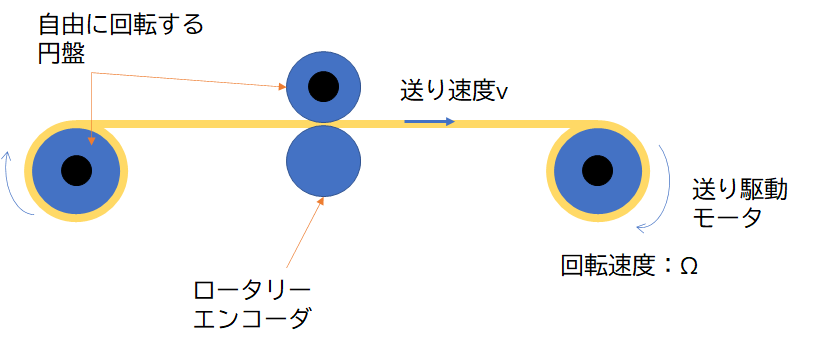
- 送り駆動モータと自由に回転する円盤で、生地同士が繋がっている
- 送り駆動モータは、半径$R_0$、一定の回転速度$\Omega$であり、入力として与えられる。(案件ではステッピングモータを使用しましたが、DCモータでも可です)
- 中間地点にロータリーエンコーダが付いており、送り速度$v$をエンコーダから読み取った値$u$を使って、等速に制御する。
- ロータリーエンコーダには極端な偏芯がないものとする
- 送る生地は、摩擦があり、円盤は滑らずに転がるものとする
応用出来そうな例
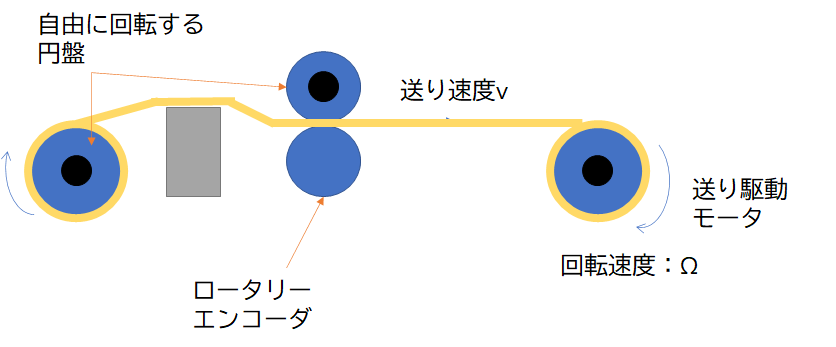
例えば、メカ構成を変えると、中間に衝立を置くような構造だったり、
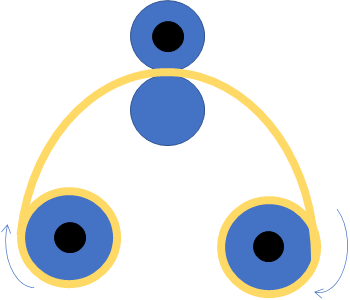
よく物理学の教科書で出てくるような一定張力の滑車の問題のような形
などに応用出来そうである。
また、今回巻いた対象物は生地であるが、トイレットペーパーを巻いたり
面白いことが出来るかもしれない。
ブロック図
通常の制御
通常はDCモータなどを使用して等速制御したり、トルクモータを使って等張力を実現したりする。
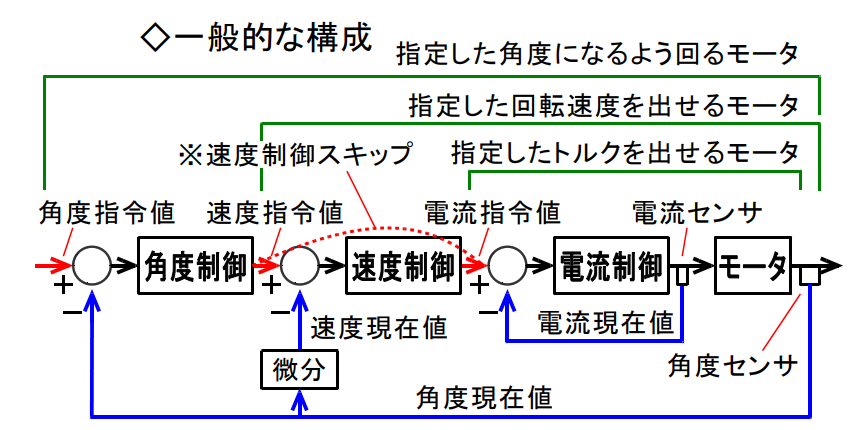
例えば、東北学院大学 熊谷教授の教材
こんな感じになっていて、DCモータの駆動入力は電流部なので、速度に変換した後、電流に変換するという2段ステップを挟む必要がある。
ステッピングモータの場合
一方で、ステッピングモータは、一定角度を同軸上に回転させるモータである。
全てパルス制御によって回転を行い、1パルスに対して同じ角度$\Delta\theta$が与えられる。
オリエンタルモータのサイトが分かりやすいだろう。
この場合、電流指令に対応する部分はパルス駆動で代替されるので、その部分が不要になり、
速度制御のパラメータが減り単純な構成となる
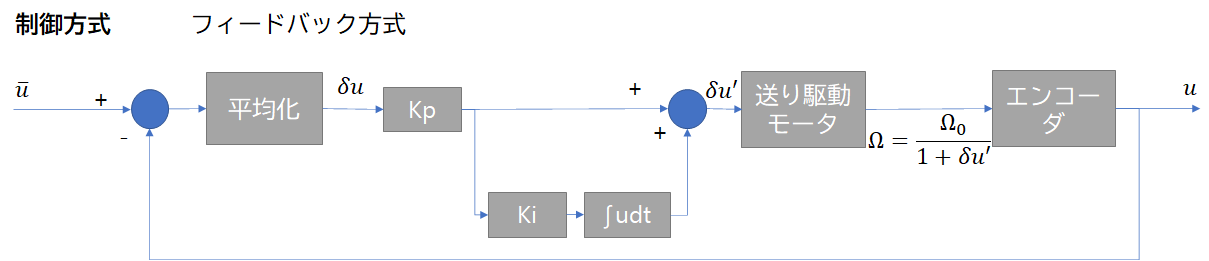
私が考えた方式がこちら
PI制御での駆動を行なう。
厳密には、エンコーダ角速度≠モータ角速度であり、角度微分はエンコーダ入力から与える必要があるが、その部分をP制御で代替し、エンコーダの角度微分(に相当するフィードバック量)を与えられるようにする。
また、I制御を追加することで、巻いたサンプルの累積誤差を抑制する。
巻取り続けると、送り駆動モータの半径が上昇し、送り駆動モータの角速度$\omega$に対して、モータ面の生地の速度$v$は上昇する。
この上昇する性質をP制御のみで行おうとすると、生地が綺麗に巻けていないときに困るので、累積値もフィードバックとすることで最適値を設定できるようにした。
速度は、エンコーダパルスが入れば入るほど、下がるように設定する。
太ってきた部分に対して、生地の面の径が大きくなるので、表面の速度が高くなるためだ。
電流制御に関しては、送り駆動モータがステップ角を与えられる。
電流が小さくなる制御の代わりに、ステップ角に対する速度を遅くする制御に切り替えた。この遅くする制御は巻き始めの角速度$\Omega_0$に対して概ね線形に変わるものと予想されたので、フィードバック量$\delta u'$が0に近い場合、巻き始めの角速度に近いものとして制御するようにした。
サンプリングは50ms単位で行い、平均化は500ms(10データ単位)で実施. Systick割り込みをVC++で生成することでサンプリングを実現
駆動側モータのローラ径は28mm
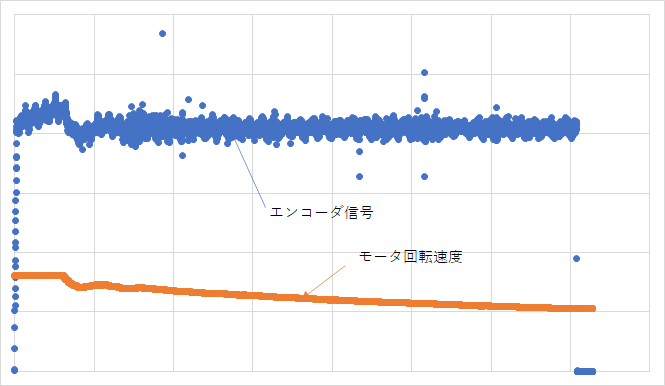
効果検証
ノイズによるバラつきはあるものの、後半ではある程度安定してエンコーダ信号が設定されていることが分かる
前半が難しい理由としては、前半は巻取り時にノイズが大きくなるためであり、この部分に関しては信号取得を省いている。
本来であればもう少し安定化も実現できる可能性があるものの、
全体を通して一定に近い速度で推移していれば良いので、今回の設計においてはこれで十分と判断した