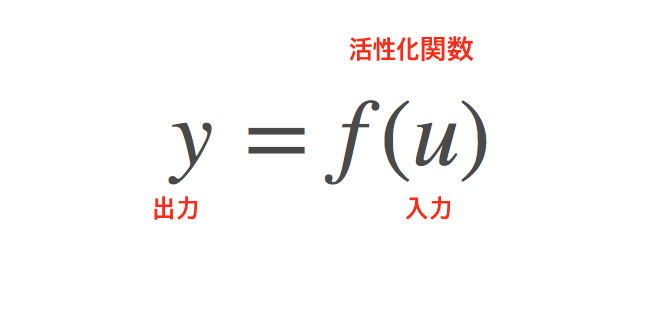はじめに
ディープラーニングやニューラルネットワークなど最近話題になっていて、誰でも一回ぐらいは聞いたことがあると思います。
しかし、いざと調べようとすると、複雑な数式や図、馴染みのない用語ばっかり出てきて理解できないことが多いかと思っております。
この記事では複雑な数式や図、用語を可能な限り一つずつ 分解&咀嚼 しながら、説明していきたいと思っております。
ニューラルネットワークとは
ウィキペディアの言葉を借りますと
ニューラルネットワークはシナプスの結合によりネットワークを形成した人工ニューロン(ノード)が、
学習によってシナプスの結合強度を変化させ、問題解決能力を持つようなモデル全般を指す
と説明しています。(シナプス?人工ニューロン?ノード?結合強度を変化?難しい、難しい。。。。。)
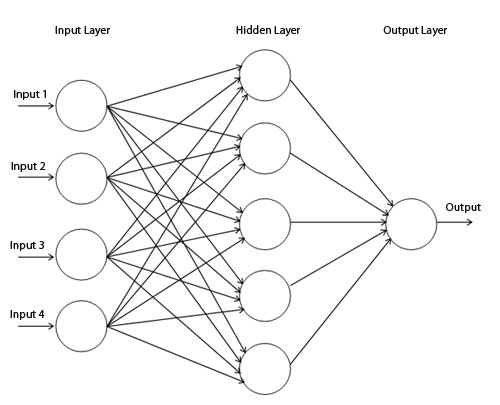
また、ニューラルネットワークで検索すると以下のような図がたくさん出てくると思います。
図1
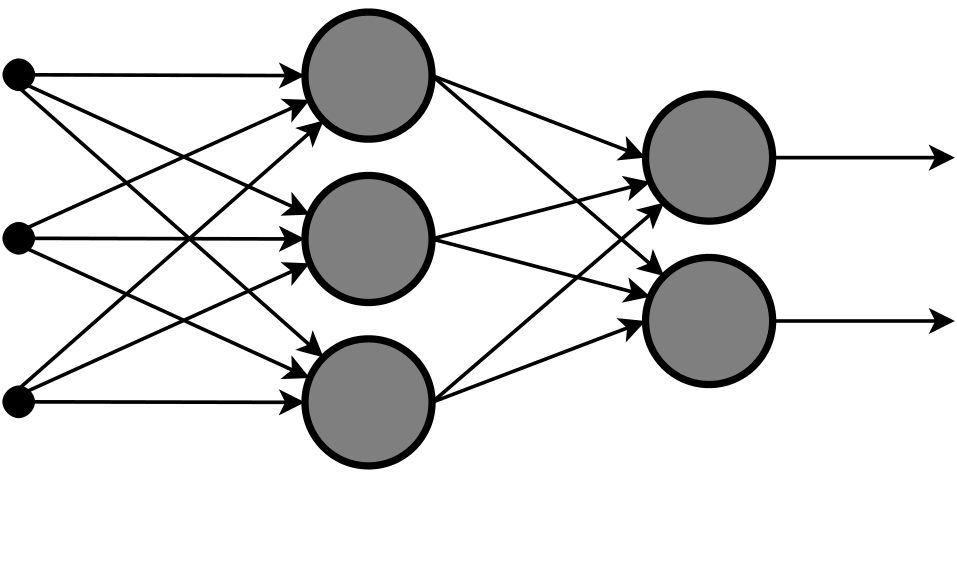
もっと頭が痛くなります。
しかし、ご心配なく。一つ一つ分解して理解していけばよいかと思います。
ニューラルネットワーク分解
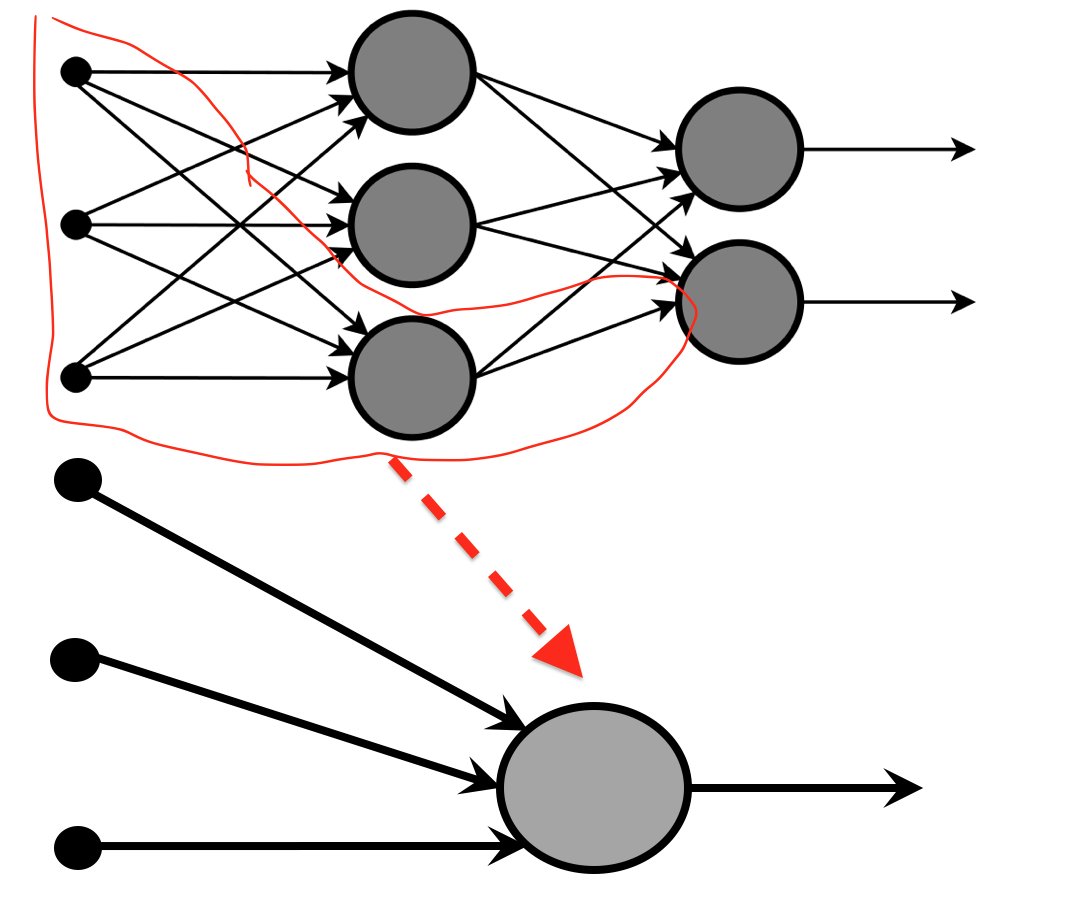
一旦、上記図が複雑そうに見えましたので、分解してみましょう。
すこしは、シンプルになったと思います。
「小さい黒い丸」の3個を「大きいグレイ丸」に__入れて(入力して)__、なんかしらを 出(出力)している ように見えます。
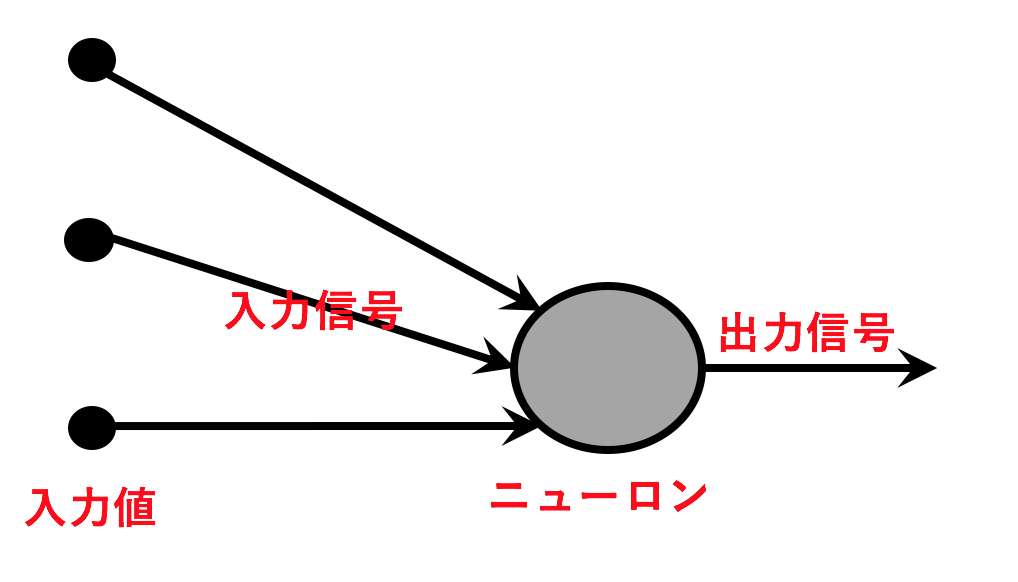
図3に名前をつけてみましょう。
• 小さい黒い丸:入力値
• 左側の矢印:入力信号(またはエッジ)
• 大きいグレイ丸:ニューロン(ノードまたは人口ニューロン)
• 右側の矢印::出力信号(またはエッジ)
※1 機械学習分野では、 ニューロン=ノード 、 信号=エッジ と考えてもよいと思います。
ちなみにTensor Flowの公式ページではノード(Node)、エッジ(Edge)と表現しています。
上記、図4のようにシンプルなネットワークを 『単純(単層) パーセプトロン(Simple Perceptron)』 といいます。『パーセプトロン』は『ニューラルネットワーク』の一種であり、起源でもあります。
このパーセプトロンはニューラルネットワークを理解する上で欠かせないものですので、簡単に説明して進めたいと思います。
パーセプトロン
パーセプトロンでは、複数の信号に 重み(結合強度) というものを乗算し足し合わせた値(u)をニューロンへ入力します。
この 重み をニューラルネットワークでは W で表現します。
入力値( u )をニューロンに入力し、またニューロンが一つの信号を出力します。
図で表すと以下の通りとなります。
数式で表すと以下の通りとなります。
(ウィキペディア参照)https://ja.wikipedia.org/wiki/活性化関数
数式1
y = f \left( \sum_{i=1}^m w_{i} x_i + b \right)
いきなり数式・記号が現れ複雑そうに見えますので、これも分解&咀嚼術で説明していきたいと思います。
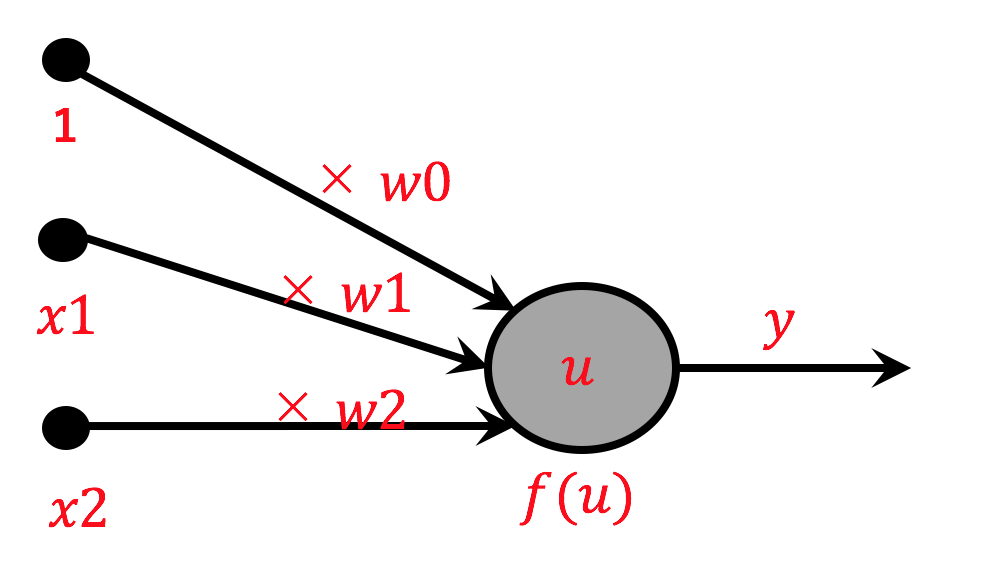
1. 重みとバイアス
まずパーセプトロン図の左側の入力する箇所をみてみましょう。
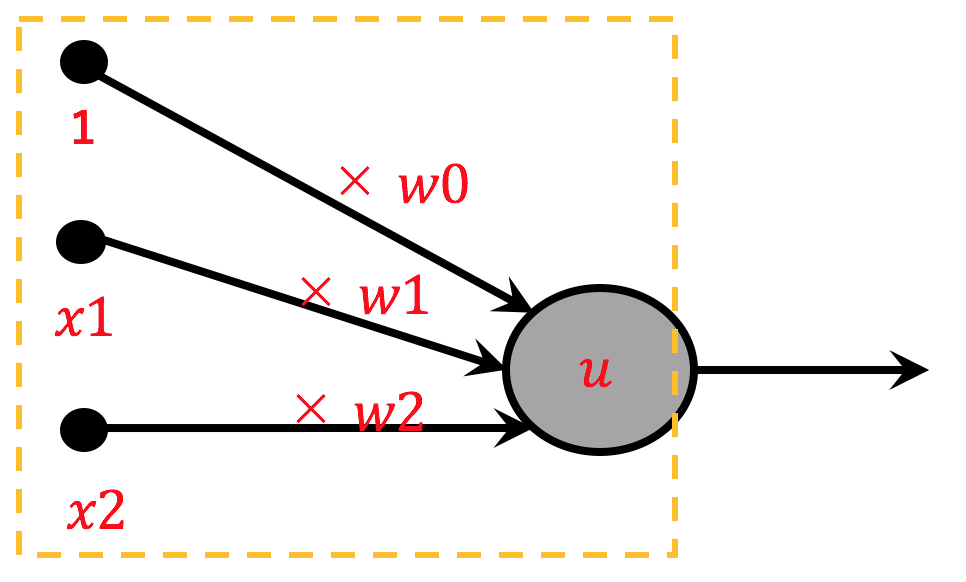
各入力信号(1, x1 , x2 )に重み( w0 , w1 , w2 )を乗算し、出し合わせます。(その値を u とします)。数式で表現すると以下の通りになります。
数式2
u = w_0 + w_1x_1 + w_2x_2
例えば、
w_0 = 1, w_1 = 2, w_2 = 3
x_1 = 4, x_2 = 1
だとします。その場合、 u の値は 12 になります。
1 + 2 × 4 + 3 × 1 = 12
ニューラルネットワークでは w0を バイアス と呼んで、 b と表記します。
数式3
u = b + w_1x_1 + w_2x_2
x1, x2,....m個まである場合は以下の数式で表現できます。
数式4
u = b + w_1x_1 + w_2x_2... w_mx_m = \sum_{i=1}^m w_{i} x_i + b
先ほど紹介した複雑な数式1は以下の通りにすこしシンプルに表現できます。
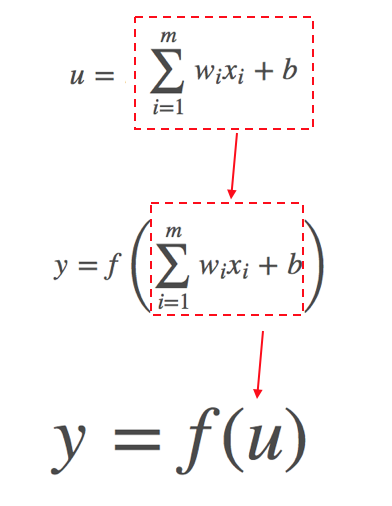
※重みとバイアスは入力値に対する係数であり、ディープラーニングで精度をきめる重要な要素であります。ここでは一旦人間が重みを決めていますが、重みも学習データーを通してコンピューターが決めるようになります。
では、次は f(u) と出力する箇所を見て見ましょう。
2. 活性化関数

上記1で算出した値 u が 『活性化関数(activation function)』 というものに入力され、変換されます。『活性化関数』を f(u) 、その出力結果を y とします。
数式で表現すると以下の通りになります。
『活性化関数』は、 入力された値を変換し新しい値を出力する変換器 だと一旦思っておいてください。
パーセプトロンの『活性化関数』の中身をみて見ましょう。
『活性化関数』は u が限界値(ここでは0とします)を超えたら1を出力し、そうでなければ0を出力します。
この『活性化関数』を数式で表すと以下の通りになります。
数式5
f(u) = \left\{
\begin{array}{ll}
1 & (u \gt 0) \\
0 & (u \leq 0)
\end{array}
\right.
※活性化関数はいくつか種類がありますが、上記のような活性化関数を『ステップ関数』と言います。
では、ここまでがパーセプトロンの説明は終わりです。パーセプトロンの内容をまとめましょう。
パーセプトロンでは、各入力信号(1, x1, x2)に重み(w0, w1, w2)を乗算し、足し合わせたものを、 活性化関数に入力し変換します。その変換結果、 y を出力します。
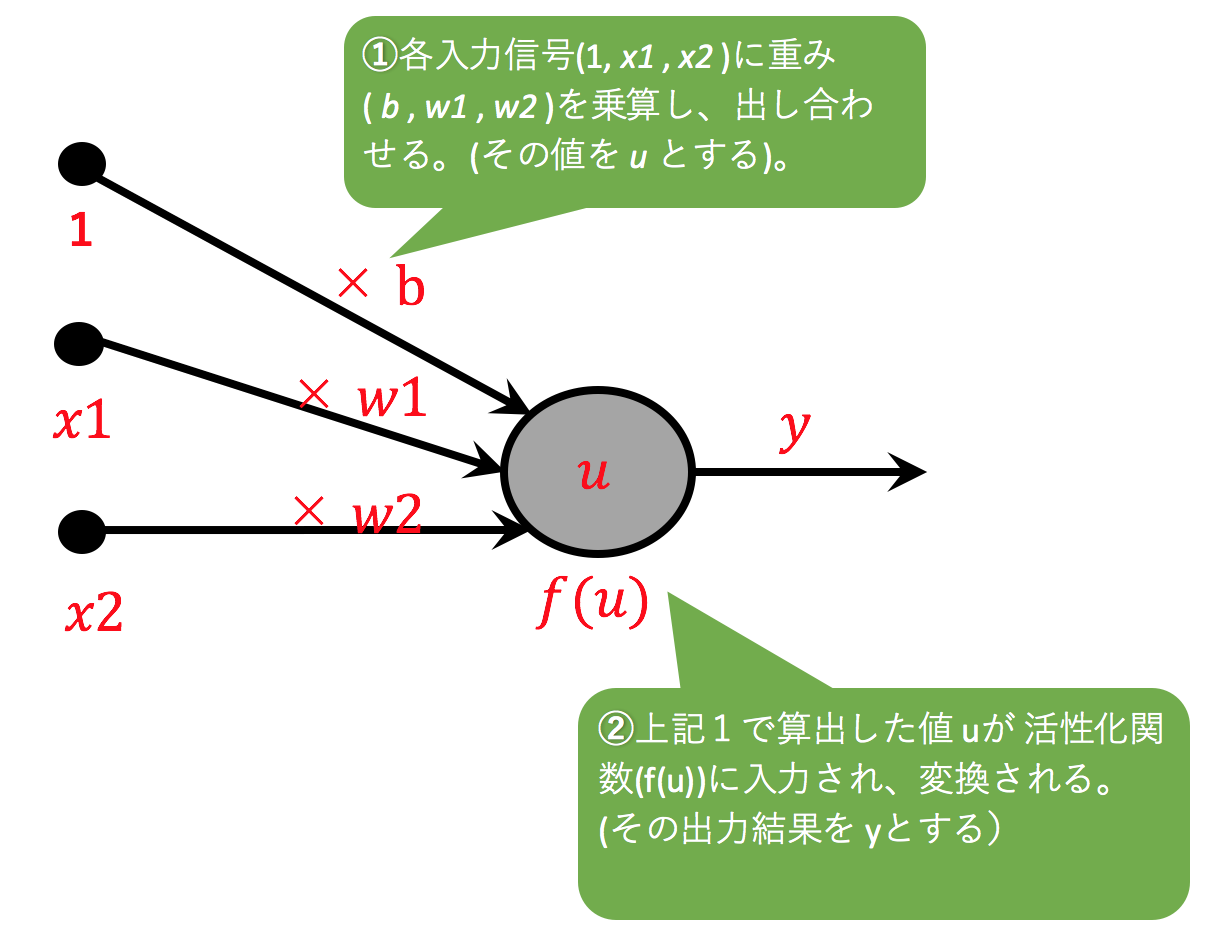

どうでしょうか。最初に複雑そうに見えた 図5 と 数式1 がすこしは理解できるようになったんでしょうか。
3. パーセプトロンでANDゲートを作る
パーセプトロンを使ってANDゲートについて考えたいと思います。
AND演算は以下の通りになると思います。
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
上記のAND演算図を満たすために、パーセプトロンの重み(w0,w1,w2)をどう設定すればよいでしょうか。
例えば、 (-0.9, 0.5, 0.5)はどうでしょうか。重みパラメーター (-0.9, 0.5, 0.5)を以下の数式に代入してみましょう。
数式
u = b + w_1x_1 + w_2x_2
y = f(u) = \left\{
\begin{array}{ll}
1 & (u \gt 0) \\
0 & (u \leq 0)
\end{array}
\right.
代入
u = -0.9 + (0.5 × 0) + (0.5 × 0) = -0.9 < 0 → 0
u = -0.9 + (0.5 × 1) + (0.5 × 0) = -0.4 < 0 → 0
u = -0.9 + (0.5 × 0) + (0.5 × 1) = -0.4 < 0 → 0
u = -0.9 + (0.5 × 1) + (0.5 × 1) = 0.1 > 0 → 1
AND演算図を満たす重みパラメータは他にも無限にあります。
では、数式だけでは、あまり面白くないと思いますので、プログラム(python)で表現してみます。
def AND(x1, x2):
b, w1, w2 = -0.9, 0.5, 0.5
u = b + w1*x1 + w2*x2
if u <= 0:
return 0
elif u > 0:
return 1
バイアス( b )は入力が0の時、出力にどれだけ値を上乗せするかを意味します。上記の例でも、入力の x1, x2 が0の時、バイアスの値だけが出力されていることがわかります。
あと、NAND, OR演算もこのようにパーセプトロンで表現できますが、説明は省略します。
多層パーセプトロン
今回は、XORゲートをパーセプトロンで表現しようと思います。
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
ANDゲートと同様にバイアス(b)と重み(w1,w2)に値を設定してXORをパーセプトロンで表現してみましょうか。
あれ?。。。表現できません。方法はないのか。
いいえ。方法はあります。パーセプトロンの 層を重ねる こと(多層)で表現できます。
まず、以下の表を見てみましょう。
| x1 | x2 | s1 | s2 | y |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
x1とx2は入力値
s1 = x1とx2のNAND演算
s2 = x1とx2のOR演算
y = s1とs2のAND演算となる。そして、x1,x2に対するXORの演算結果でもある。
プログラムで記載すると以下の通りになると思います。
def XOR(x1, s2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
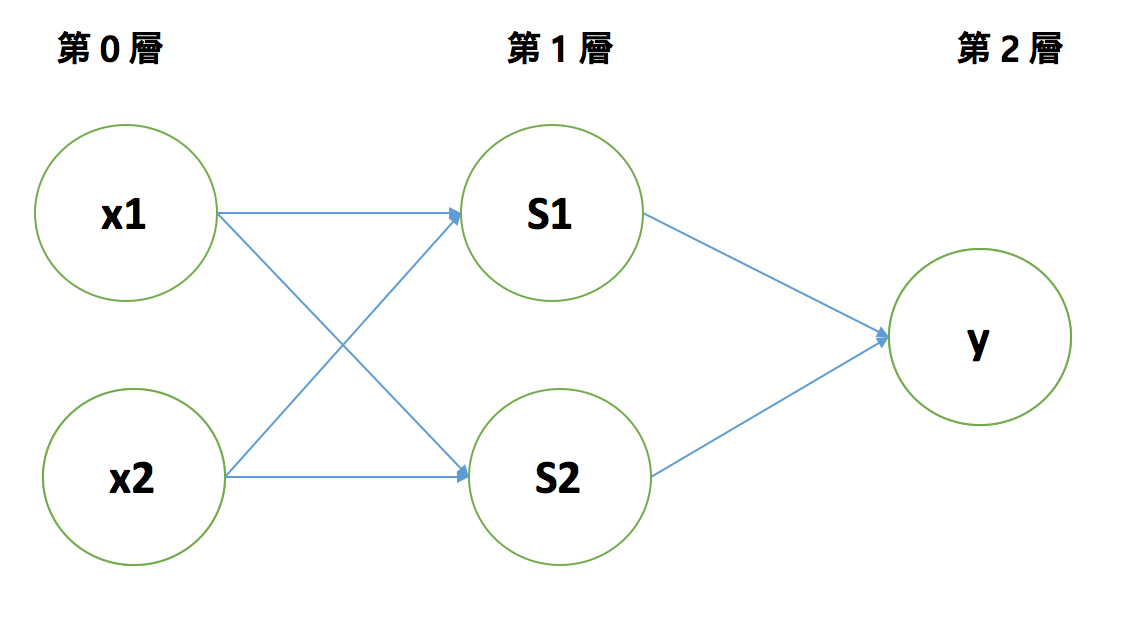
複数の第0層の信号を第1層のニューロンへ入力し、結果を出力します。その結果をまた第2層ニューロンへ入力し、 y を出力します。
これを 『多層パーセプトロン(Multilayer Perceptron)』 と言います。このように『単純パーセプトロン』に対して 層を重ねる ことで『多層パーセプトロン』ができます。
もっとノードを増やし、もっと層を重ねると、最小に紹介した図2のようになります。
このように 『多層パーセプトロン』 を ほぼ 『ニューラルネットワーク』 と言います。
なぜ、 ほぼ なのか。それは、『ニューラルネットワーク』 で使用する 『活性化関数』に違いがある ためです。
これで、重み、バイアス、パーセプトロン、そしてニューラルネットワークについての説明は終わりです。
(もし、余力があれば)次回、 ニューラルネットワークでの活性化関数 に関して説明したいと思います。
参考
https://www.nextobe.com/single-post/2017/05/16/퍼셉트론
http://hokuts.com/2015/11/25/ml2_perceptron/
https://ja.wikipedia.org/wiki/ニューラルネットワーク
https://ja.wikipedia.org/wiki/活性化関数
本「ゼロから作るDeep Learning」