株式会社ブレインパッドでデータサイエンティストをしている23新卒の泉です。

この記事はBrainPad Advent Calender 2023 24日目の記事シリーズ2です。

今日はクリスマスイブですね。ということで「ツリー」に関連して決定木について紹介します。

Bayesian CARTとは

Bayesian CART(Bayesian classification and regression tree)は、Chipmanら(1998)において提案されたベイズ的な考え方に基づく決定木です。

Bayesian CARTの概要は次の通りです。

決定木とその終端ノードを確率変数とみなした上で尤度と事前分布を設定し、決定木の事後分布を導出します。
決定木の事後分布からメトロポリス・ヘイスティングス法を用いて大量の決定木をサンプリングします。
サンプリングした決定木の事後確率をもとに「よい」決定木を選択します。

本記事では1のみを説明し、2と3については割愛します。これらに関してはChipmanら(1998)を参照してください。

事前分布で罰則を課す

Bayesian CARTにおいて注目すべき点は、事前分布を用いて複雑なモデルに罰則を与えることです¹。これによって過学習を抑制することができます。

通常の決定木でも過学習を抑制する手続きは存在します。
そのため、ベイズ化の長所とは必ずしも言えないですが、Bayesian CARTの応用モデルでは重要なアイデアとなります。

Bayesian CARTは発展モデルがホット

Bayesian CARTが単体で利用されることは多くありませんが、因果推論の文脈で注目を集めるモデルにおける核となっており、その意味で重要です。
例えば、Chipmanら(2010)のBART(Bayesian additive regression trees)はBayesian CARTのアンサンブルによるモデルになっています。²

事後分布の導出

Bayesian CARTの目標は決定木の事後分布を得ることです。その導出を以下の流れに沿って説明します。

決定木の事後分布が、尤度・決定木の事前分布・終端ノードの事前分布の3つを用いて表現できることを示します。
尤度を設定します。
決定木の生成を確率過程として表現し、これを決定木の事前分布として設定します。
終端ノードの事前分布を設定します。

尤度と事前分布を定めれば事後分布が定まり、これを推論に利用するのがベイズ統計の枠組みです。

ノーテーション

$b$個の終端ノードを持つ決定木について以下の記号を導入します。

$T$：決定木
$M=\{\mu_{1},\ldots,\mu_{b}\}$：終端ノードのパラメータ$\mu_{i}$の集合

ベイズ流の設定に基づき、$T$と$\mu_{i}$が事前分布を持つ確率変数であることに注意します。なお、決定木$T$が確率変数であるというのは、 ノードの分割有無と分割ルールが確率的に生成される ことを意味します。このことは事前分布の設定において説明します。

説明変数と被説明変数については以下の記号を導入します。

$x=(x_1,\ldots,x_p)$：$p$次元の説明変数
$Y=(Y_1,\ldots,Y_b)$：$b$個の終端ノードに割り当てられる被説明変数
$Y_i=(y_{i1},\ldots,y_{in_{i}})$：終端ノード$i$に割り当てられる$n_i$個の被説明変数

決定木の事後分布

決定木の事後分布は

\begin{align}
p(T|x,Y) &\propto  p(T)p(Y|x,T) \\
&=p(T)\int p(Y|x,M,T)p(M|T)dM \tag{1}
\end{align}

と書けます。それぞれ$p(Y|x,M,T)$は尤度、$p(T)$は決定木の事前分布、$p(M|T)$は決定木が与えられた下での終端ノードの事前分布です。

以下ではそれぞれのパーツに関して導出します。

尤度

終端ノードのパラメータ集合$M$と決定木$T$が所与の下での$n=\sum^b_{i=1}n_i$個のデータの尤度は

\begin{align}
p(Y|M,T,x) &= \prod^b_{i=1}f(Y_i|\mu_i,T)\\
&= \prod^b_{i=1}\prod^{n_i}_{j=1}f(y_{ij}|\mu_i,T)
\end{align}

とします。ここで、$M$と$T$が所与の下で$n$個の$y_{ij}$が終端ノード内・終端ノード間で独立同分布に従うと仮定することに注意します。

確率分布$f$はタスクに応じて設定します。回帰タスクであれば平均パラメータが$\mu_{i}$の正規分布を用い、分類問題であればパラメータが$\mu_{i}$のベルヌイ分布を用いることが多いです。

決定木の事前分布

$T$の事前分布$p(T)$は確率分布として陽に与えるのではなく、以下のステップで表される確率過程として設定します。

ノードを1つしか持たない決定木を$T$とする
確率$p_{SPLIT}$でノードを分割する
2でノードが分割された場合、ある分割ルール(分割に使う$x_i$と分割の閾値)を確率$p_{RULE}$で割り当て、子ノードを作成する
作成された子ノードに対し、2と3を繰り返す

後はノード分割の確率$p_{SPLIT}$と分割ルールの割り当て確率$p_{RULE}$を設定すればよいです。

ノード分割の確率

Chipmanら(1998)ではハイパーパラメータ$\alpha$と$\beta$を用いて、深さ$d$のノードを$p_{SPLIT}=\alpha (1+d)^{-\beta}$で分割しています。

この確率に従ってノードを分割すると、複雑な決定木が生成されにくいことを確認します。

以下は論文からの抜粋で、$p_{SPLIT}$の$\alpha,\beta$を様々に指定して決定木を生成したときの終端ノードの個数の分布です。いずれも2~3個がピークで、そこからは確率が小さくなる様子が確認できます。

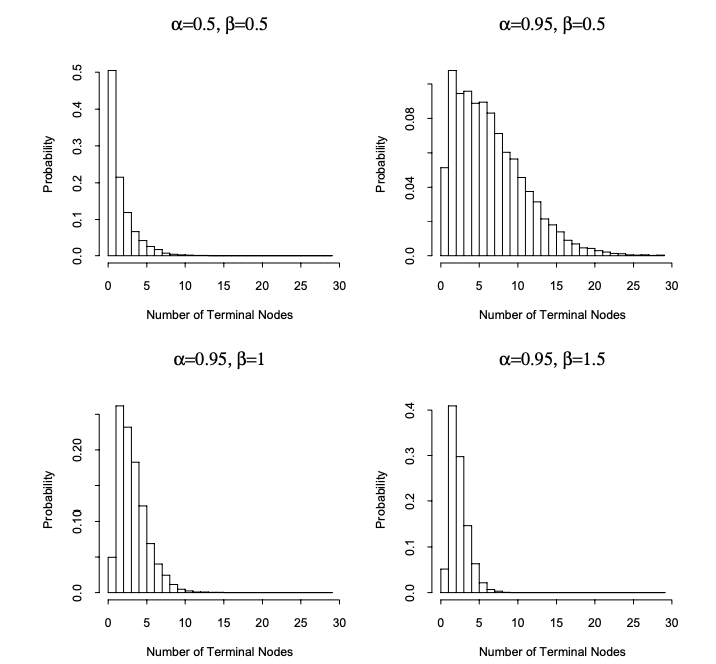
分割ルールの割り当て確率

分割ルールは、$x=x(x_1,\ldots,x_p)$のうち分割に使う$x_i$を選択と、分割の閾値の設定とに分けられます。
これらの確率には一様分布を設定します。つまり、$x_i$の選択ではどの$x_i$も確率$1/p$で等しく選択し、閾値の設定では選択した$x_i$の全ての値から等確率でいずれかの値を閾値に設定します。

終端ノードの事前分布

決定木$T$が与えられた下での終端ノード$M$の事前分布$p(M|T)$には、サンプリングの都合に鑑みて共役事前分布を設定します。したがって、タスクに応じて設定する確率分布$f$によって設定すべき事前分布は異なります。

例として回帰タスクを考えます。このとき$f$は正規分布とするのでした。簡単のためにこの正規分布の分散は既知とします。³ 尤度は

y_{i1},\ldots,y_{in_{i}}|\mu_i,T\text{ 〜 } Normal(\mu_i,\sigma^2)

となります。このとき事前分布を

\mu_1,\ldots,\mu_b|T\text{ 〜 } Normal(\mu^{*},\sigma^{2*})

と設定すると、解析的に事後分布が得られます。

まとめ

以上で(1)における尤度$p(Y|x,M,T)$・決定木の事前分布$p(T)$・終端ノードの事前分布$p(M|T)$を得て、事後分布$p(T|x,Y)$が得られました！

最後に

今回はベイズ的方法に基づく決定木であるBayesian CARTを紹介しました。最初にも述べた通り、単体で用いられることは多くないですが、BARTなどの発展モデルの一部として活躍しているモデルです。発展モデルのキャッチアップの一助になれば嬉しいです。

事前分布によって罰則を与えるアプローチは、ベイズ機械学習の枠組みではしばしば用いられます。
パラメータに適切な事前分布を設定すると、複雑なモデルに罰則を課すことができます。例えば、線形回帰モデルの回帰パラメータの事前分布を正規分布としてMAP推定すると、その解はリッジ回帰（線形回帰の$L^2$正則化）の結果に一致します。(例えば須山(2019))。 ↩
元々は予測モデルとして提案されたものの、Hill(2011)で因果推論への応用可能性が示唆されました。2016年には因果推論コンペAtlantic Causal Inference Conferenceにおいて優れた性能を示しました。 ↩
この記事では簡単のために尤度を分散が既知の正規分布としましたが、Chapmanら(1998)では分散未知という一般的な設定を考えています。その場合には分散にも事前分布を考える必要があり、逆ガンマ分布を用いると解析的に事後分布が得られることが知られています。共役事前分布の設定についてはベイズ統計学のテキストを参照してください。(例えばHoff(2009)) ↩

ベイズ的方法に基づく決定木:Bayesian CART