ラビットチャレンジ学習レポート：深層学習day3

Section1：再帰型ニューラルネットワークの概念

■RNNとは
・自然言語や時系列データなど連続的なつながりのあるデータに対応可能な、ニューラルネットワークである。
・時系列データとは、時間的順序を追って一定間隔ごとに観察され、しかも相互に統計的依存関係が認められるようなデータの系列
→音声データ、テキストデータ
・時系列モデルを扱うには、初期の状態と過去の時間$t-1$の状態を保持し、そこから次の時間での$t$を再起的に求める再帰構造が必要になる。

■RNNの学習イメージ

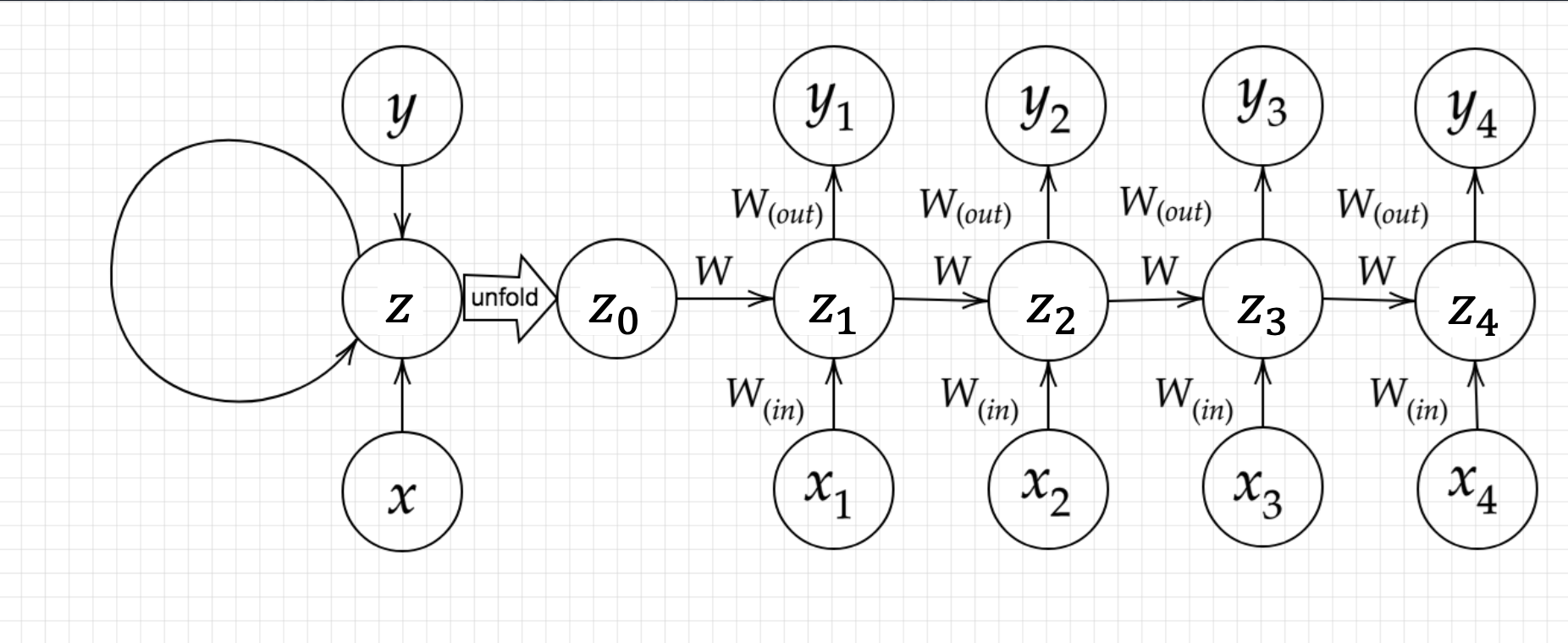
※$x$：入力層、$y$：出力層、$z$：中間層
・中間層からの出力を次の中間層へ入力する
・次の時間では、前の中間層から受け取った状態と入力層の内容をもとに出力を出す

■RNNの数学的記述
$u^t = W_{(in)}x^t+Wz^{t-1}+b$
$z^t = f{(W_{(in)}x^t+Wz^{t-1}+b)}$
$v^t = W_{(out)}z^t+c$
$y^t = δ(W_{(out)}z^t+c)$

■BPTT（Backpropagation Through Tiime）
・BPTTとはRNNにおいてのパラメータ調整方法の一種
　→誤差逆伝播の一種
　　→誤差逆伝播法とは、計算結果から微分を逆算することで、不要な再帰的計算を避けて微分を算出できる。

実装演習

▼重みを変化させて実行
・サンプルのRNNのコードを実行

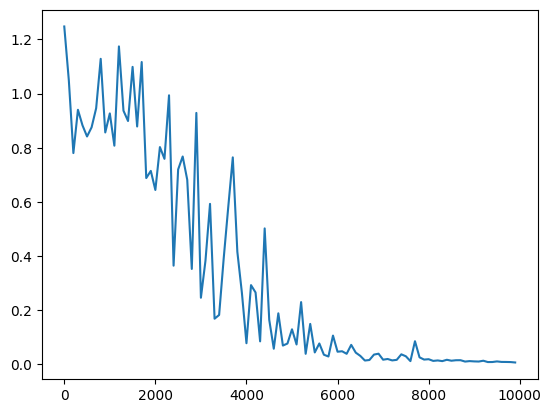
→学習回数が増えるにつれ、誤差がうまく収束していっていることが分かる。

・重みの初期化方法をXavierに変更

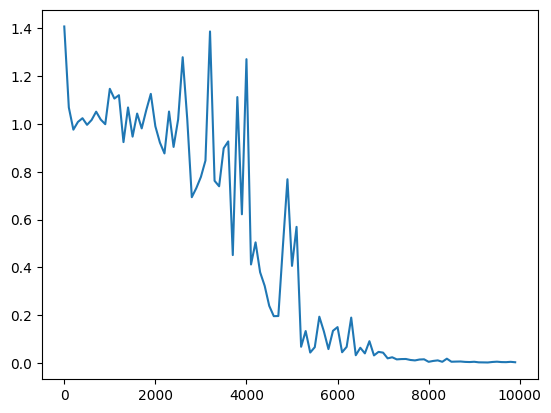
→先ほどより収束するのに時間がかかっているが、学習回数が増えるにつれ、誤差がうまく収束していっていることが分かる。

・重みの初期化方法をHeに変更

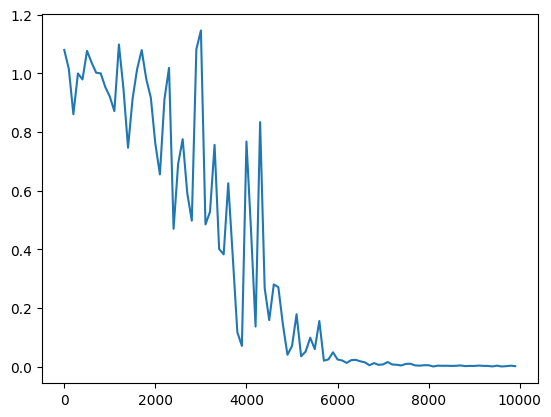
→Xavierより収束スピードが早い。学習回数が増えるにつれ、誤差がうまく収束していっていることが分かる。

▼標準偏差を変化させて実行
・サンプルのRNNで、標準偏差を1→0.5へ変更。

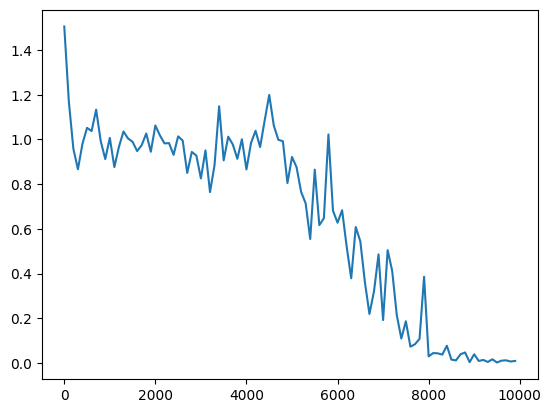
・重みの初期化方法をXavierで、標準偏差を1→0.5へ変更

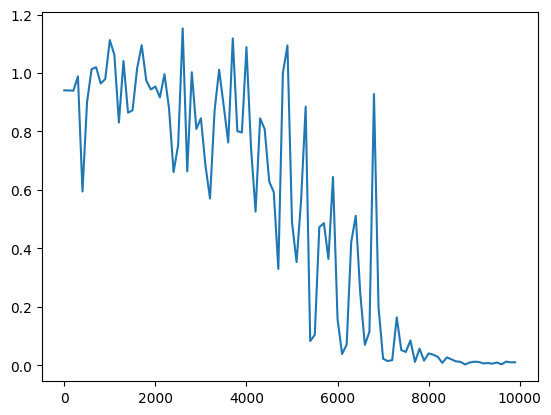
・重みの初期化方法をHeで、標準偏差を1→0.5へ変更

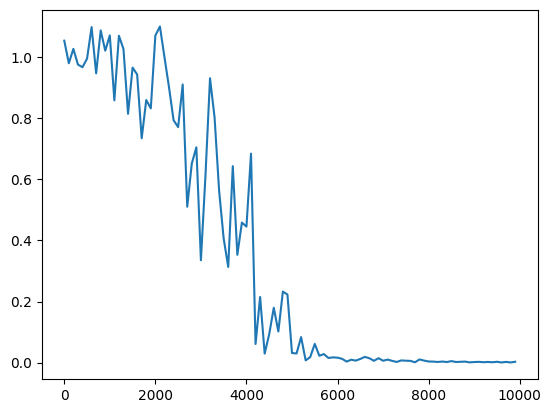
→どれも収束するのに時間がかかるようになった

▼学習率を変化させて実行
・サンプルのRNNで、学習率を0.1→0.5へ変更

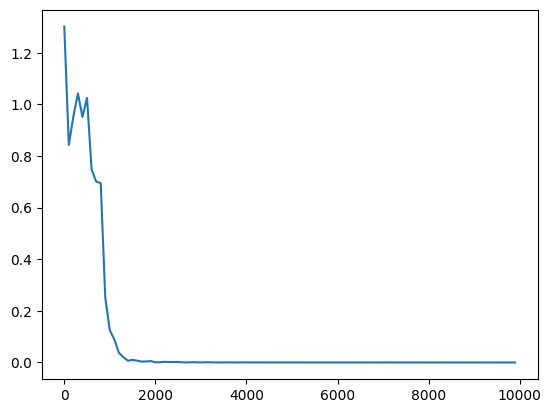
・重みの初期化方法をXavierで、学習率を0.1→0.5へ変更

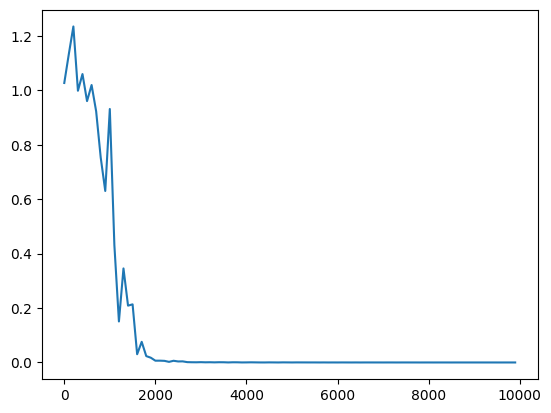
・重みの初期化方法をHeで、学習率を0.1→0.5へ変更

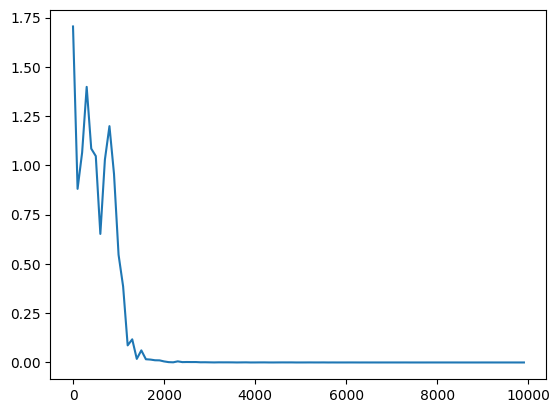
→どれも早い段階で収束した。

▼隠れ層のサイズを変更
・サンプルのRNNで、隠れ層を16→8へ変更

・サンプルのRNNで、隠れ層を16のまま実行

・サンプルのRNNで、隠れ層16→32へ変更

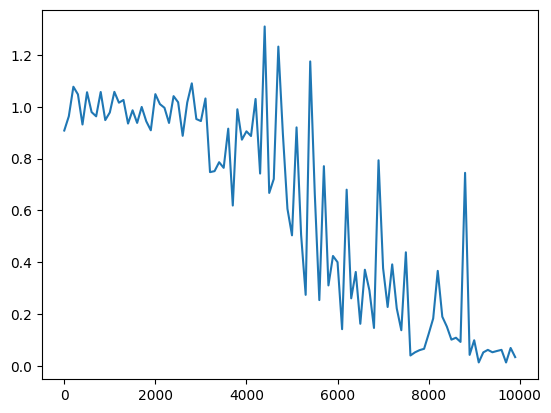
→隠れ層のサイズが16が一番収束が早かった。
→隠れ層のサイズをさらに大きくしたからといって、収束が早まるわけではないようだ。

・中間層の活性化関数をReLuへ変更

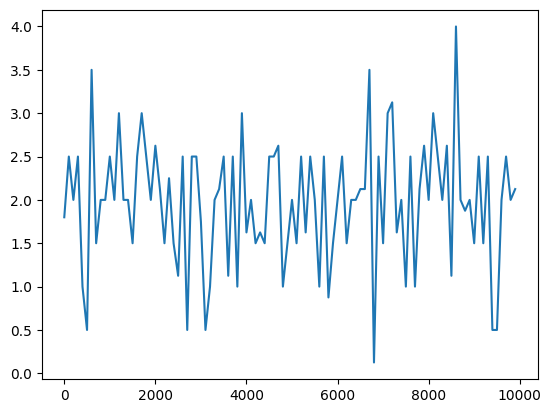
→勾配爆発によるためか、誤差が安定しなくなった。

確認テスト

Q：RNNのネットワークには大きくわけて3つの重みが ある。1つは入力から現在の中間層を定義する際にかけられる重み、1つは中間層から出力を定義する際にかけられる重みである。 残り1つの重みについて説明せよ。
A：現在の中間層から次の時刻の中間層への重み。次の時間では、前の中間層から受け取った状態と入力層の内容をもとに出力を出す

Q：連鎖律の原理を使い、dz/dxを求めよ。$z=t^2$、$t=x+y$
A：$dz/dx = (dz/dt)(dt/dx)$と表現できる。
$dz/dt=2t$
$dt/dx=1$
つまり、$dz/dx=(dz/dt)(dt/dx)=(2t)(1)=2t$

Q：下図のy1をx・z0・z1・win・w・woutを用いて数式で表せ。
　　※バイアスは任意の文字で定義せよ。 ※また中間層の出力にシグモイド関数g(x)を作用させよ。

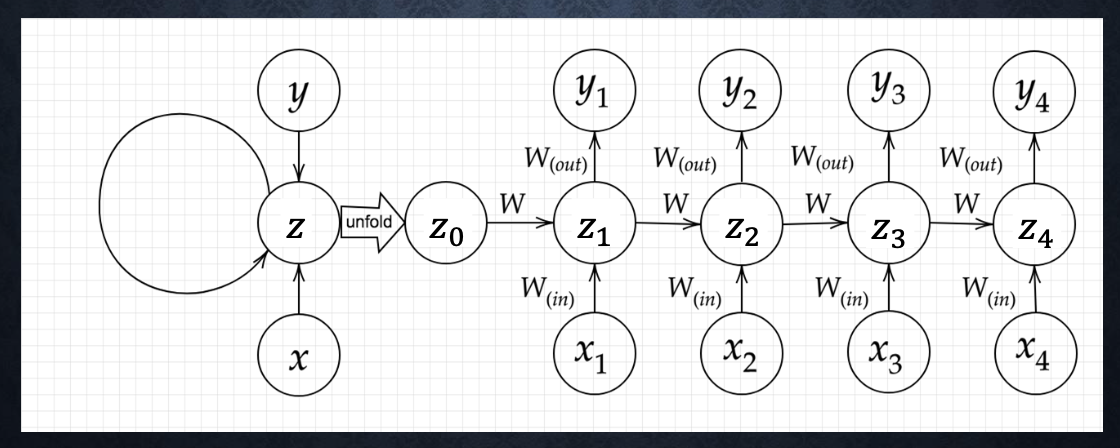
A：まず、z1は以下のように表せる。
$z_1=g(W_{in}x_1+W{z_0}+b)$
※$b$はバイアス項
続いて、y1は以下のように表せる。
$y_1=W_{out}z_1+c$
※$c$はバイアス項
これらをまとめると
$y_1=g(W_{out}(W_{in}x_1+W{z_0}+b)+c)$

Section2：LSTM

■RNNの課題
・時系列を遡れば遡るほど、勾配が消失していく。
・長い時系列の学習が困難。
・LSTMにより解決

■勾配消失問題
・誤差逆伝播法が下位層に進んでいくにつれて、勾配がどんどん緩やかになっていく。そのため、勾配降下法による、更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。
・活性化関数としてシグモイド関数を使っていては、大きな値では出力の変化が微小なため、勾配消失問題を引き起こすことがあった。

■勾配爆発
・勾配爆発とは、勾配が層を逆伝播するごとに指数関数的に大きくなっていくこと。
・勾配爆発を防ぐために勾配のクリッピングを行うという手法がある。
　→勾配のノルムがしきい値を超えたら、勾配のノルムをしきい値に正規化するというもの。

■LSTMの全体像

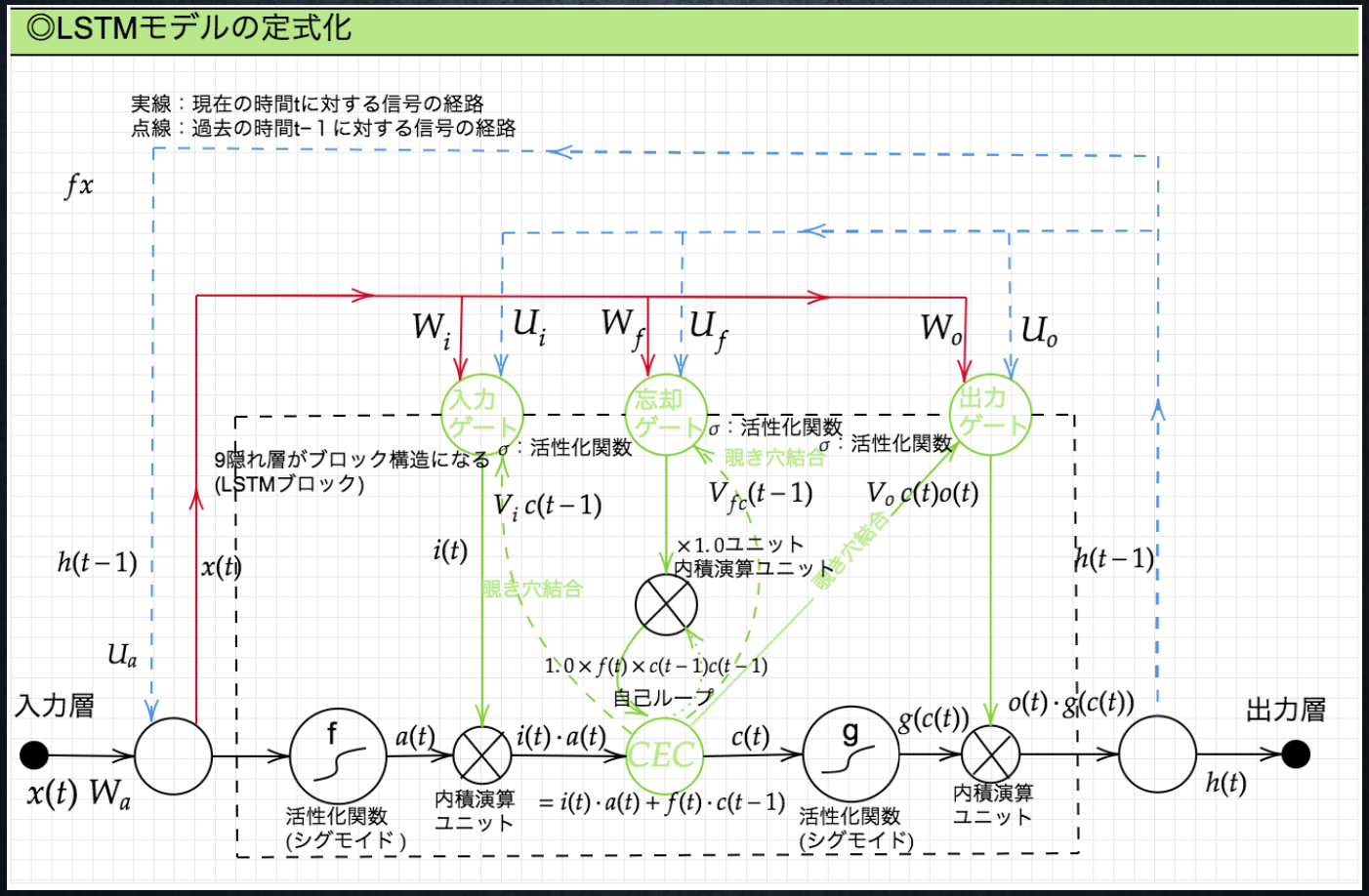
・LSTM：Long Short Term Memory
・CECという記憶セルと入力ゲート、出力ゲート、忘却ゲートというデータの流れをコントロールする３つのゲートから構成される

・CEC（Constant Error Carousel）
RNNでいう中間層。誤差を内部に閉じ込める役割を持ち、勾配消失を防ぐ。別名、セルと呼ばれる。CECは記憶機能のみ持ち、学習特性がない。

・入力ゲート
CECに入力する情報としてどれだけ価値があるかを判断する。今回の入力値と前回の出力値をもとに、CECに追加する情報の取捨選択を行う。

・出力ゲート
次の隠れ層への出力を司るゲート。次にどれだけ情報を通すかは、入力値と前の状態から求める。

・忘却ゲート
CECは過去の情報が入らなくなった場合、削除することができないため、CECに対して「何を忘れるか」を明示的に指示し不要な記憶を忘れさせる役割を持つ。

・覗き穴結合
CECに保存されている過去の情報を、任意のタイミングで他のノードに伝播させたり、忘却させたりすることを目的として作られた。通常、CECの値はゲート制御には影響を与えないが、覗き穴結合ではCECの値を重み行列を介して伝播可能にする。この構造により、ゲート制御においてもCECの値が影響を与えるようになる。しかし、この試みは失敗に終わった模様。

実装演習

なし

確認テスト

Q：シグモイド関数を微分した時、入力値が0の時に最大値 をとる。その値として正しいものを選択肢から選べ。 (1)0.15 (2)0.25 (3)0.35 (4)0.45
A：シグモイド関数は$σ(x)=\frac{1}{1+e^{-1}}$
微分すると、$σ'(x)=σ(x)(1-σ(x))$
x=0の時
$σ'(0)=σ(0)(1-σ(0))=\frac{1}{2}・\frac{1}{2}=\frac{1}{4}=0.25$
→(2)0.25

Q：以下の文章をLSTMに入力し空欄に当てはまる単語を予測したいとする。文中の「とても」という言葉は空欄の予測において、なくなっても影響を及ぼさないと考えられる。このような場合、どのゲートが作用すると考えられるか。
「映画おもしろかったね。ところで、とてもお腹が空いたから何か____。」
A：忘却ゲート。「とても」は空欄部分の予測には影響しない。

Section3：GRU（Gated Recurrent Unit）

・従来のLSTMではパラメータ数が多く、計算負荷が高くなる問題があった。しかし、GRUではそのパラメータを大幅に削減し、精度は同等またはそれ以上が望めるようになった構造のこと。

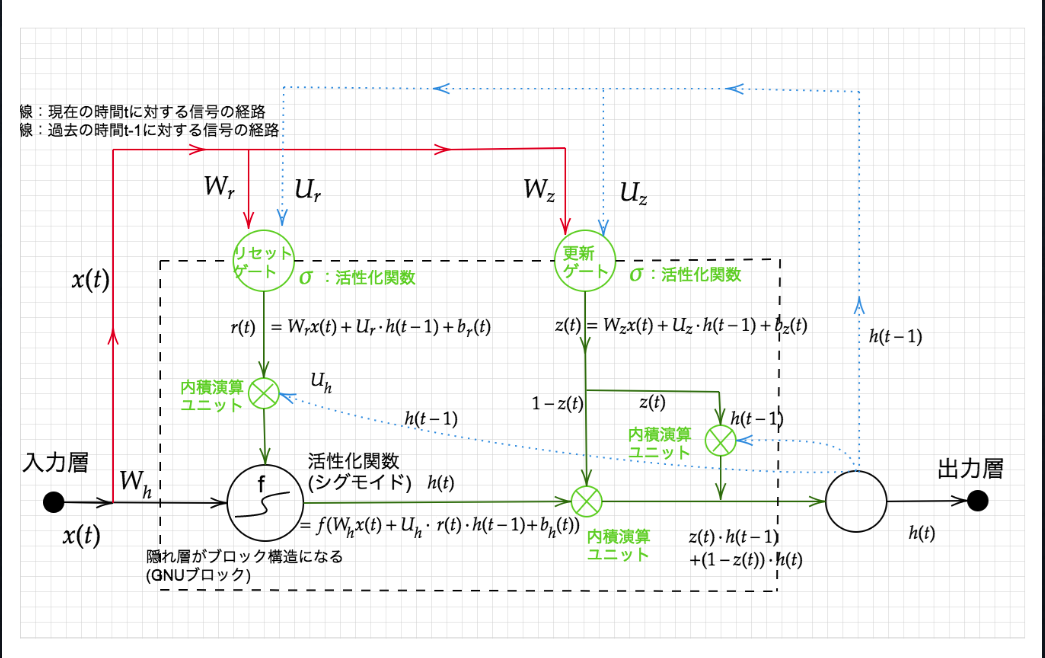
・リセットゲートと更新ゲートが登場。どちらのゲートも、今回の入力と前回の出力を元に隠れ層の状態をどのような状態で保持するかコントロールする。

実装演習

・実装演習用のソースコードがなかったため、演習チャレンジから抜粋

def gru(x, h, W_r, U_r, W_z, U_z, W, U):
    #ゲートを計算
    #リセットゲート
    r = _sigmoid(x.dot(W_r.T) + h.dot(U_r.T))
    
    #更新ゲート
    z = _sigmoid(x.dot(W_z.T) + h.dot(U_z.T))

    #次状態を計算
    h_bar = np.tanh(x.dot(W.T) + (r * h).dot(U.T))
    h_new = (1 - z) * h + z * h_bar
    return h_new

確認テスト

Q：LSTMとCECが抱える課題について、それぞれ簡潔に述べよ。
A：LSTMはパラメータ数が多くなり計算量が多い。CECは勾配が１で学習特性がない。

Q：LSTMとGRUの違いを簡潔に述べよ。
A：LSTMは入力ゲート、忘却ゲート、出力ゲートの３つのデータの流れをコントロールするゲートとCECという記憶セルから構成される。たくさんのゲートを使うので、計算パラメータが多く計算量が多くなる。GRUはLSTMをシンプルにしたもの。LSTMの計算パラメータが多い問題を解決し、計算精度の向上を図ったもの。

Section4：双方向RNN

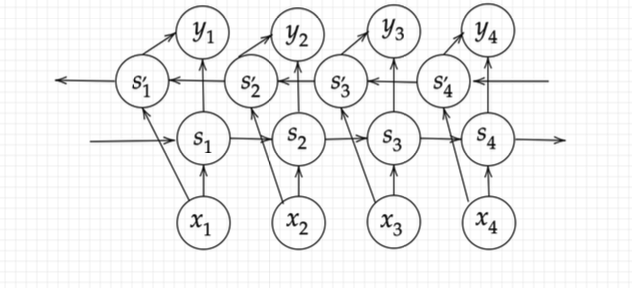
・過去の情報だけでなく、未来の情報を加味することで、精度を向上させるためのモデル
→実用例：文章の推敲、機械翻訳など

実装演習

・実装演習用のソースコードがなかったため、演習チャレンジから抜粋

def bidirectional_rnn_net(xs, W_f, U_f, W_b, U_b, V):

    # 順方向と逆方向の入力シーケンスを初期化
    xs_f = np.zeros_like(xs)
    xs_b = np.zeros_like(xs)

    # 順方向と逆方向の入力シーケンスを設定、xs_fはそのまま、xs_bは逆順に設定
    for i in enumerate(xs):
        xs_f[i] = x
        xs_b[i] = x[::-1]

    # 順方向RNNの隠れ状態を計算
    hs_f = rnn(xs_f, W_f, U_f)

    # 逆方向RNNの隠れ状態を計算
    hs_b = rnn(xs_b, W_b, U_b)

    # 順方向RNNと逆方向RNNの隠れ状態を結合
    hs = [np.concatenate([h_f, h_b[::-1]], axis=0) for h_f, h_b in zip(hs_f, hs_b)]
    ys = hs.dot(V.T)
    return ys

確認テスト

確認テストなしのため、「ゼロつく2」からもう少し補足を書く。
双方向RNNでは、逆方向に処理するLSTMレイヤも追加する。そして、各時刻において、２つのLSTMレイヤの隠れ状態を連結し、それを最終的な隠れ状態ベクトルとする。このように双方向から処理することで、各単語に対応する隠れ状態ベクトルは、左と右の両方向からの情報を集約することができる。それによって、バランスの取れた情報がエンコードされる。
LSTMの実装方法は、２つのLSTMレイヤを使って、それぞれのレイヤに与える単語の並びを調整する。具体的には、１つのLSTMレイヤにはこれまで通りの入力文を与える。これは入力文を「左から右方向」に処理する一般的なLSTMレイヤである。一方、もう１つのLSTMレイヤには入力文の単語を右から左方向の並びとして与える。（→元の文章：「ABCD」の場合、「DCBA」の並びに変える）
この並びを変えた文章を与えることで、もう１つのLSTMレイヤは入力文を「右から左方向」に処理することになる。後は、その２つのLSTMレイヤの出力を連結するだけで、双方向LSTMレイヤが出来上がる。
→人間では時系列方向からしか処理できないが、機械だと、逆方向の処理も可能なので、これらを組み合わせることで処理精度の向上を図ろうと発想したのが面白いと思った。

Section5：Seq2Seq（Sequence to Sequence）

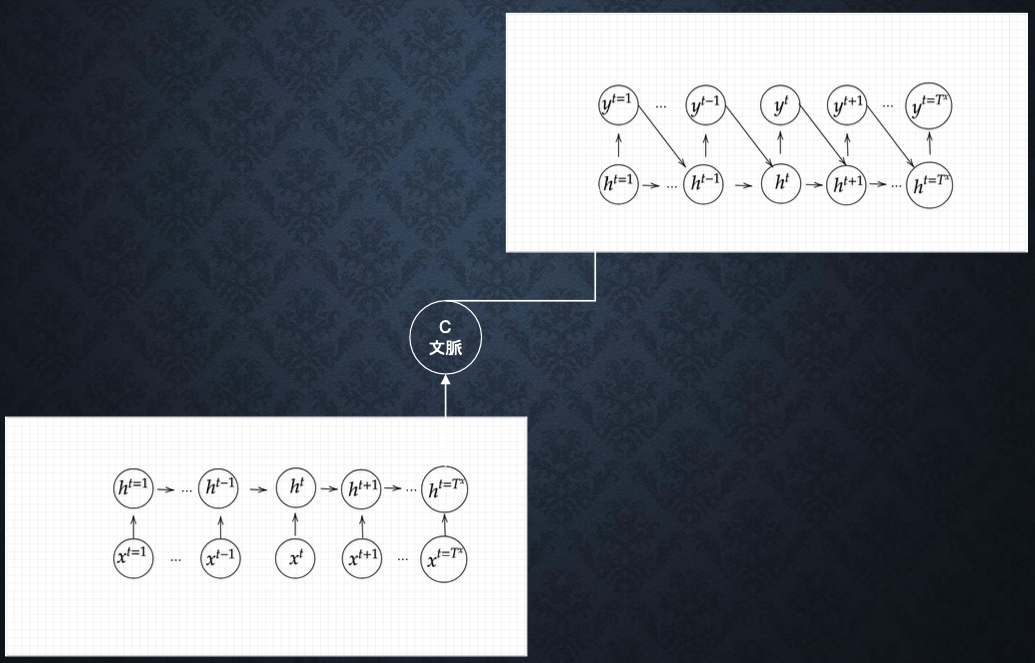
・Seq2Seqとは、Encoder-Decoderモデルの一種を指す。
→機械対話や、機械翻訳に使用
※左下：Encoderモデル、右上：Decoderモデル

■Encoder RNN

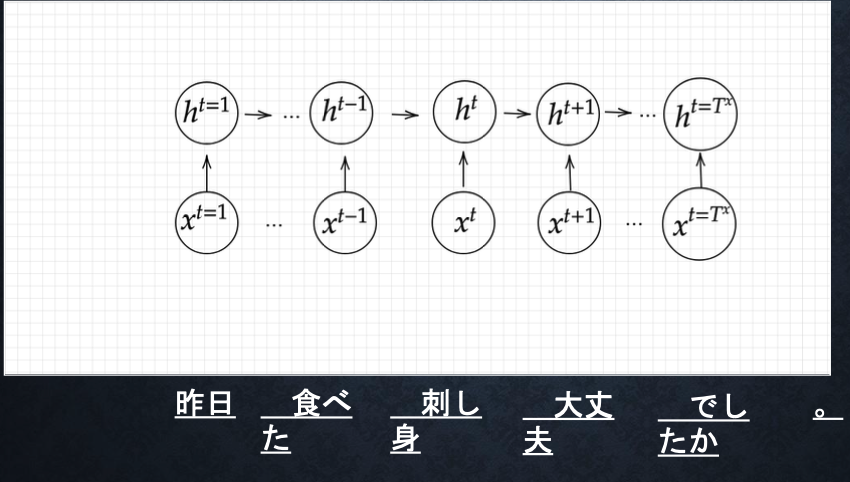
・ユーザーがインプットしたテキストデータを、単語等のトークンに区切って渡す構造。
※Taking：文章を単語などのトークン毎に分割し、トークンごとのIDに分割する
※Embedding：IDから、そのトークンを表す分散表現ベクトルに変換
※Encoder RNN：ベクトルを順番にRNNに入力していく。
・処理手順
1.vec1をRNNに入力し、hidden stateを出力。このhidden stateと次の入力vec2をまたRNNに入力してきたhidden stateを出力という流れを繰り返す。
2.最後のvecを入れた時のhidden stateをfinal stateとして取っておく。このfinal stateがthought vectorと呼ばれ、入力した文の意味を表すベクトルとなる。

■Decoder RNN

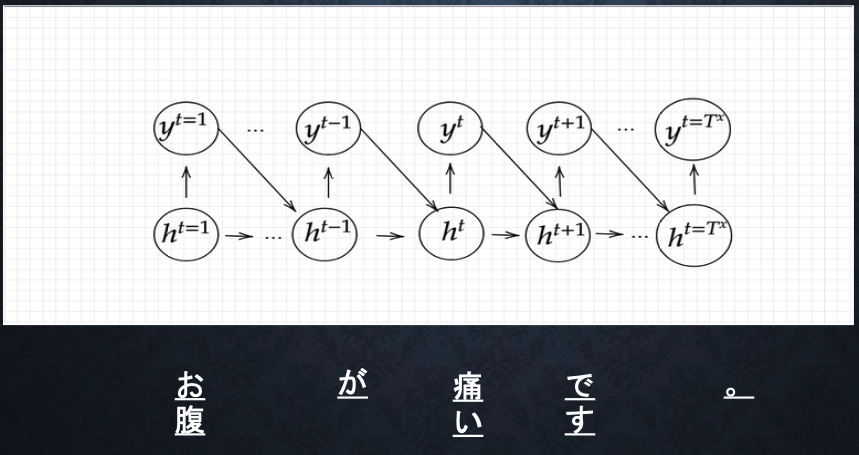
・システムがアウトプットデータを、単語等のトークンごとに生成する構造。
・処理手順
1.Decoder RNN：Encoder RNNのfinal state（thought vector）から、各tokenの生成確率を出力していきfinal stateをDecoder RNNのinitial stateとして設定し、Embeddingを入力。
2.Sampling：生成確率に基づいてtokenをランダムに選ぶ。
3.Embedding：2で選ばれたtokenをEmbeddingしてDecoder RNNへの次の入力とする。
4.Detokenize：1-3を繰り返し、2で得られたtokenを文字列に直します。

■HRED
・Seq2Seqの課題は一問一答しかできないことであり、問いに対して文脈も何もなく、ただ応答が行われ続ける。
・HREDとは、過去n-1個の発話から次の発話を生成する。
→Seq2Seqでは、会話の文脈無視で、応答がなされたが、HREDでは、前の単語の流れに即して応答されるため、より人間らしい文章が生成される。
・HREDの構造：Seq2Seq + Context RNN
→Context RNNとは、Encoderのまとめた各文章の系列をまとめて、これまでの会話コンテキスト全体を表すベクトルに変換する構造のことであり、これにより過去の発話の履歴を加味した返答をできる。
・HREDの課題
　・HREDは確率的な多様性が字面にしかなく、会話の「流れ」のような多様性がない。
　　→同じコンテキスト（発話リスト）を与えられても、答えの内容が毎回会話の流れとしては同じものしか出せない。
　・HREDは短く情報量に乏しい答えをしがちである。
　　→短いよくある答えを学ぶ傾向がある。
　　（例）うん、そうだね、など

■VHRED
・VHREDとは、HREDに、VAE（Variational Autoencoder：変分オートエンコーダ）の潜在変数の概念を追加したもの。
→HREDの課題を、VAEの潜在変数の概念を追加することで解決した構造。
※VAEはディープラーニングによる生成モデルの１つで、訓練データを元にその特徴を捉えて訓練データセットに似たデータを生成することができるもの。

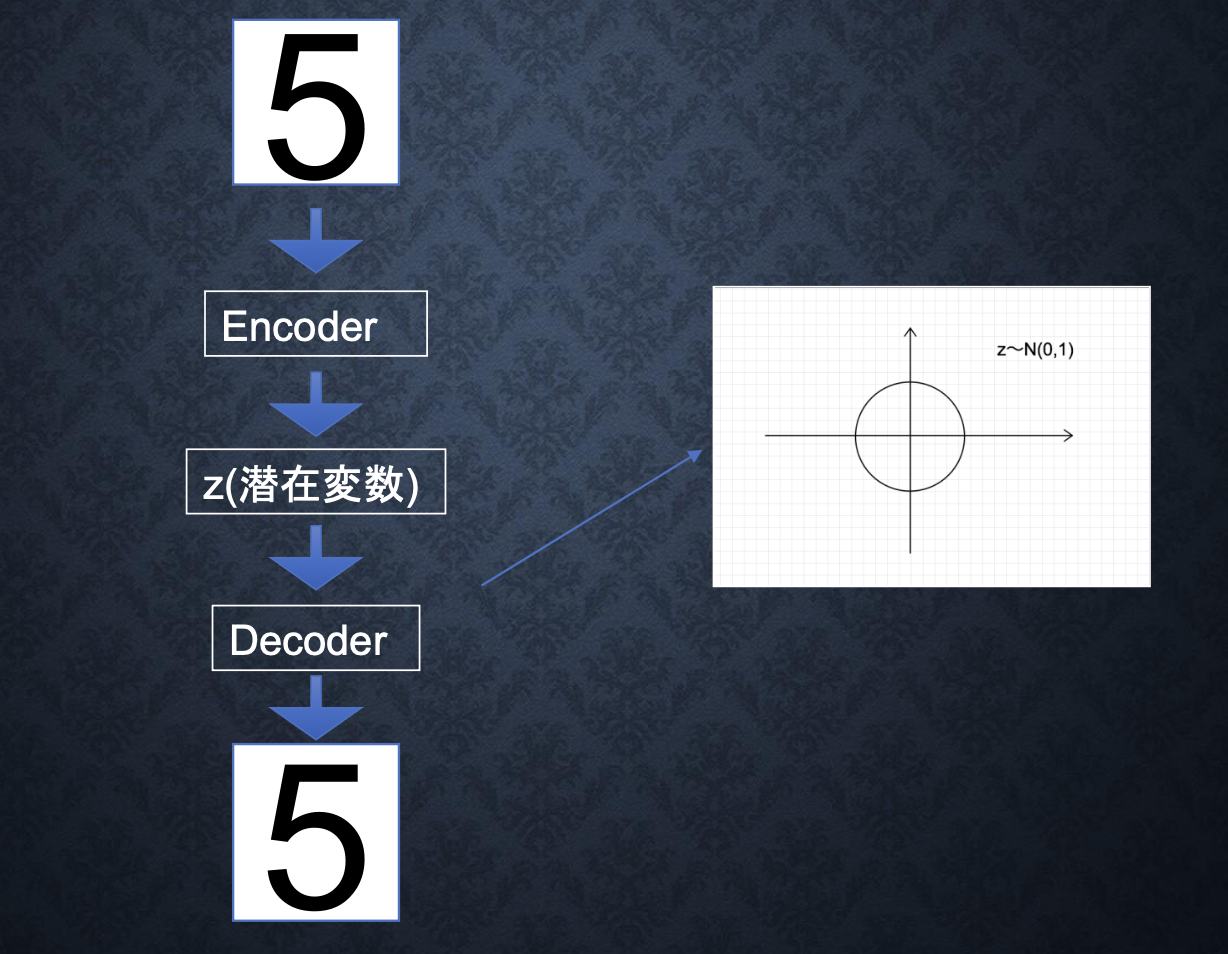
■VAE（Variational Autoencoder：変分オートエンコーダ）
・オートエンコーダとは、教師なし学習の一つ。そのため、学習時の入力データは訓練データのみで教師データは利用しない。
→具体例：MNISTの場合、28*28の数字の画像を入れて、同じ画像を出力するニューラルネットワークということになる。
・オートエンコーダ構造
→入力データから潜在変数zに変換するニューラルネットワークをEncoder、逆に潜在変数zをインプットとして元画像を復元するニューラルネットワークをDecoderにした構造。メリットとしては、次元削減が行えること。
※zの次元が入力データより小さい場合、次元削減とみなすことができる。

・VAE
通常のオートエンコーダーの場合、何かしら潜在変数zにデータを押し込めているものの、その構造がどのような状態かわからない。VAEはこの潜在変数zに確率分布z∼N(0,1)を仮定したもの。VAEは、データを潜在変数zの確率分布という構造に押し込めることを可能にする。

・VAE構造

確認テスト

Q：下記の選択肢から、seq2seqについて説明しているものを選べ。
(1)時刻に関して順方向と逆方向のRNNを構成し、それら2つの中間層表現を特徴量として利用するものである。
(2)RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる。
(3)構文木などの木構造に対して、隣接単語から表現ベクトル(フレーズ)を作るという演算を再 帰的に行い(重みは共通)、文全体の表現ベクトルを得るニューラルネットワークである。
(4)RNNの一種であり、単純なRNNにおいて問題となる勾配消失問題をCECとゲートの概念を 導入することで解決したものである。
A：（2）

Q：seq2seqとHRED、HREDとVHREDの違いを簡潔に述べよ。
A：Seq2Seq：Encoder-Decoderモデルの一種。一問一答しかできないことが課題。
HRED：過去n-1個の発話から次の発話を生成する。確率的な多様性が字面にしかなく、会話の「流れ」のような多様性がないことが課題。
VHRED：HREDにVAEの潜在変数の概念を追加したもの。HREDの課題を解決し字面だけではない多様な返答ができるようになった。

Q：VAEに関する下記の説明文中の空欄に当てはまる言葉を答えよ。
自己符号化器の潜在変数に____を導入したもの。
A：確率分布

Section6：Word2vec

・RNNでは、単語のような可変長の文字列をNNに与えることはできない。
→固定長形式で単語を表す必要がある。
・Word2vecでは、学習データからボキャブラリを作成する。
例：I want to eat apples. I like apples.
→{apples,eat,I,like,to,want}
・メリット
→大規模データの分散表現の学習が、現実的な計算速度とメモリ量で実現可能にした。
→ボキャブラリ×ボキャブラリだけの重み行列から、ボキャブラリ×任意の単語ベクトル次元で重み行列が誕生

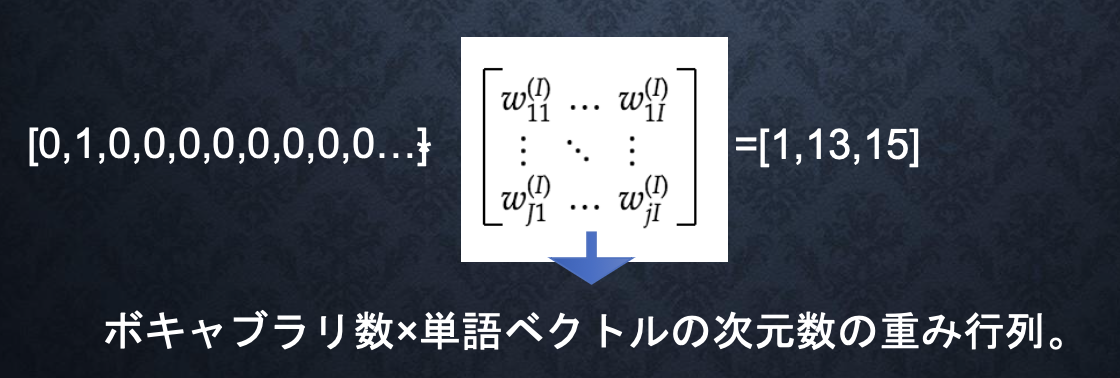
■one-hotベクトル
・applesを入力する場合は、入力層には以下のベクトルが入力される。
※本来は、辞書の単語数だけone-hotベクトルができあがる。

実装演習

なし

確認テスト

なし

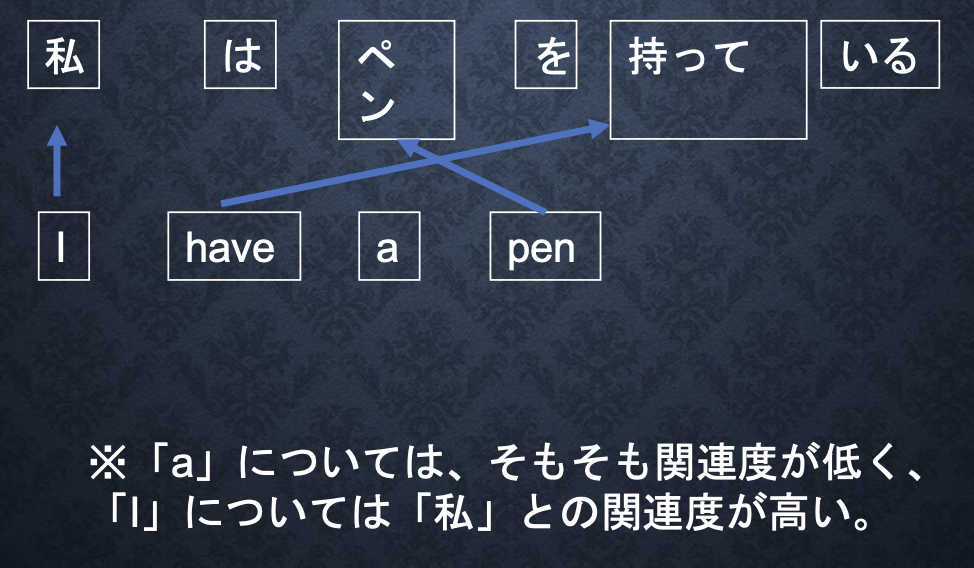
Section7：Attention Mechanism

・seq2seqの課題は長い文章への対応が難しいこと。seq2seqでは、2単語でも、100単語でも、固定次元ベクトルの中に入力しなければならない。
→解決策：文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていく。Attention Mechanism：「入力と出力のどの単語が関連しているのか」の関連度を学習する仕組みにより解決。

実装演習

なし

確認テスト

Q：RNNとword2vec、seq2seqとAttentionの違いを簡潔に述べよ。
A：RNNとword2vec：
RNN：時系列データなど連続的なつながりのあるデータに対応可能なニューラルネットワーク
word2vec：単語の意味をベクトルで表現する手法

seq2seqとAttention：
seq2seq：Encoder-Decoderモデルの一種で、会話の文脈無視で応答がなされる
Attention：入力と出力のどの単語が関連しているのか関連度を学習し、応答する

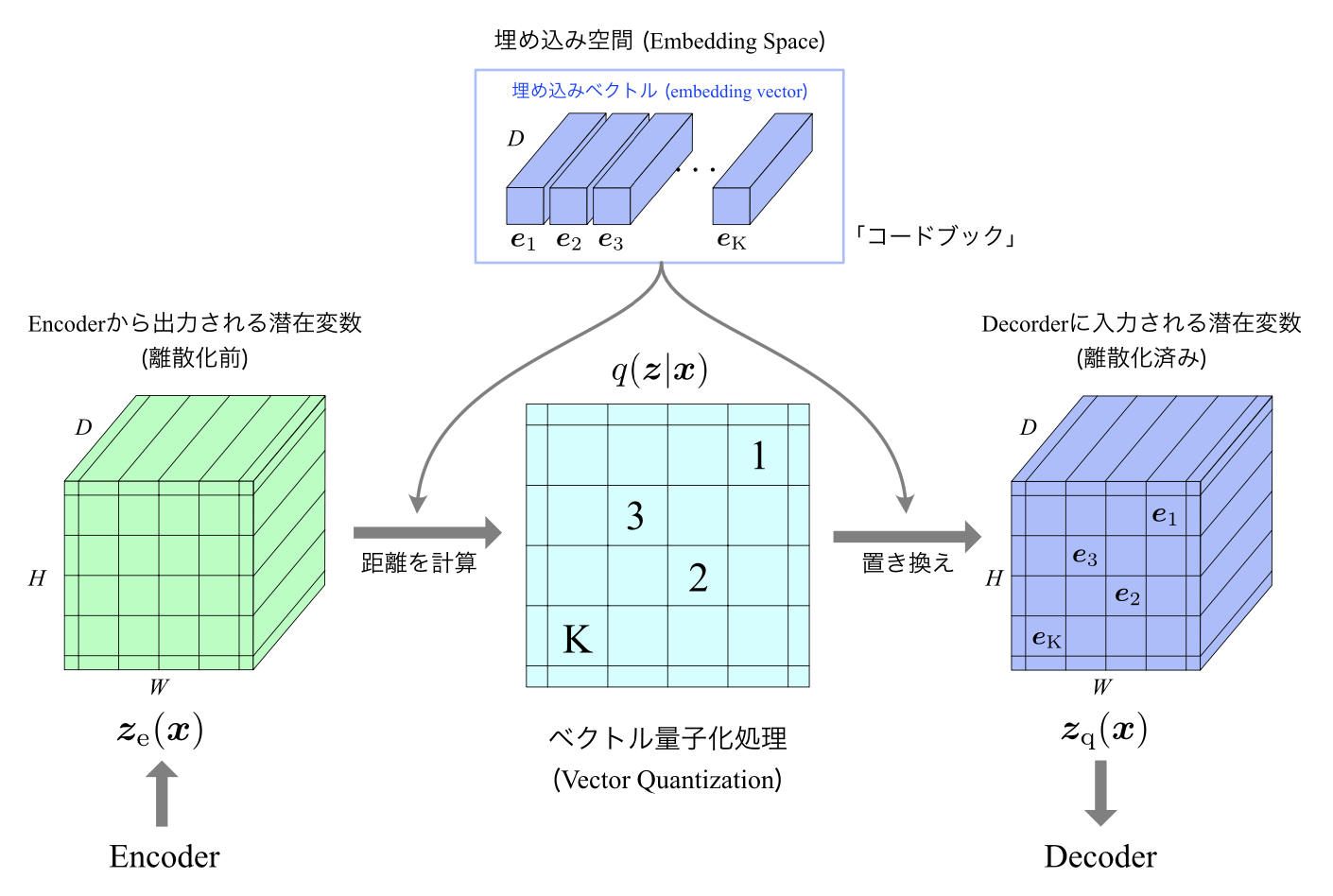
VQ-VAE（Vector Quantised-Variational AutoEncoder）

・VAE (Variational AutoEncoder) の派生技術にあたる生成モデル
・潜在変数が離散値となるように学習が行われる。これにより、従来のVAEで起こりやすいとされる “posterior collapse”の問題を回避し、高品質のデータを生成することが可能となった

■VAEとVQ-VAEの比較

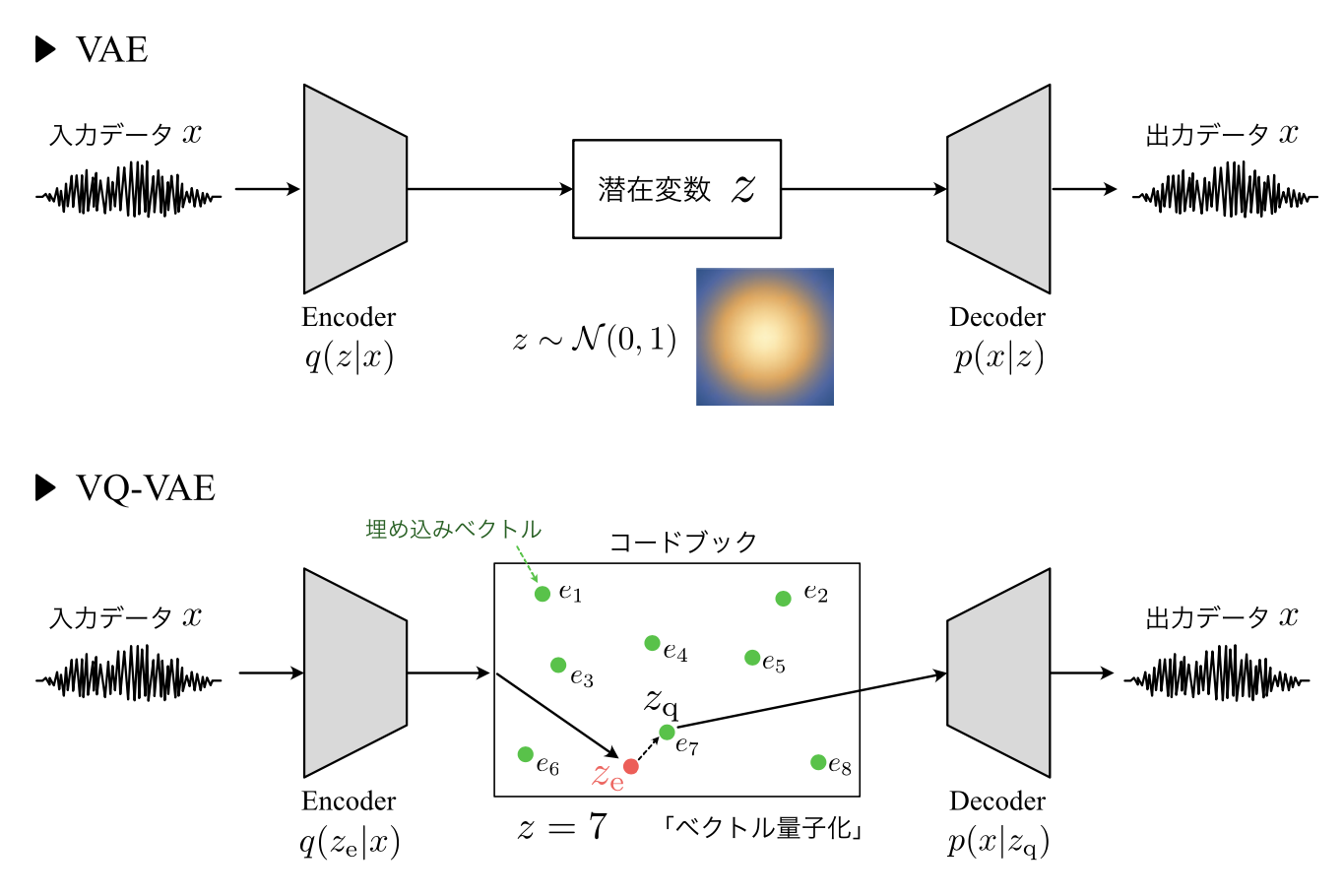
・両者ともベースの構造はオートエンコーダで、「入力を潜在表現にエンコード→潜在表現から入力を再構成」という構造は同じ
・VAE：潜在変数zがGauss分布に従うベクトルになるように学習を行う
・VQ-VAE：潜在変数zが離散的な数値となるように学習を行う

■VQ-VAEのアーキテクチャ

実装演習キャプチャ

なし

確認テスト

なし

[フレームワーク演習] 双方向RNN / 勾配クリッピング

・双方向RNN：過去の情報だけでなく、未来の情報を加味することで、精度を向上させるためのモデル
・勾配クリッピング：誤差逆伝播法を実行するときに時折発生する勾配爆発問題に対処するために使用される手法。勾配の上限値を定義することで、勾配爆発が抑制されます。

実装演習キャプチャ

・双方向RNN

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers

tf.keras.backend.clear_session()
model_4 = tf.keras.models.Sequential()
model_4.add(layers.Input((NUM_DATA_POINTS, 1)))
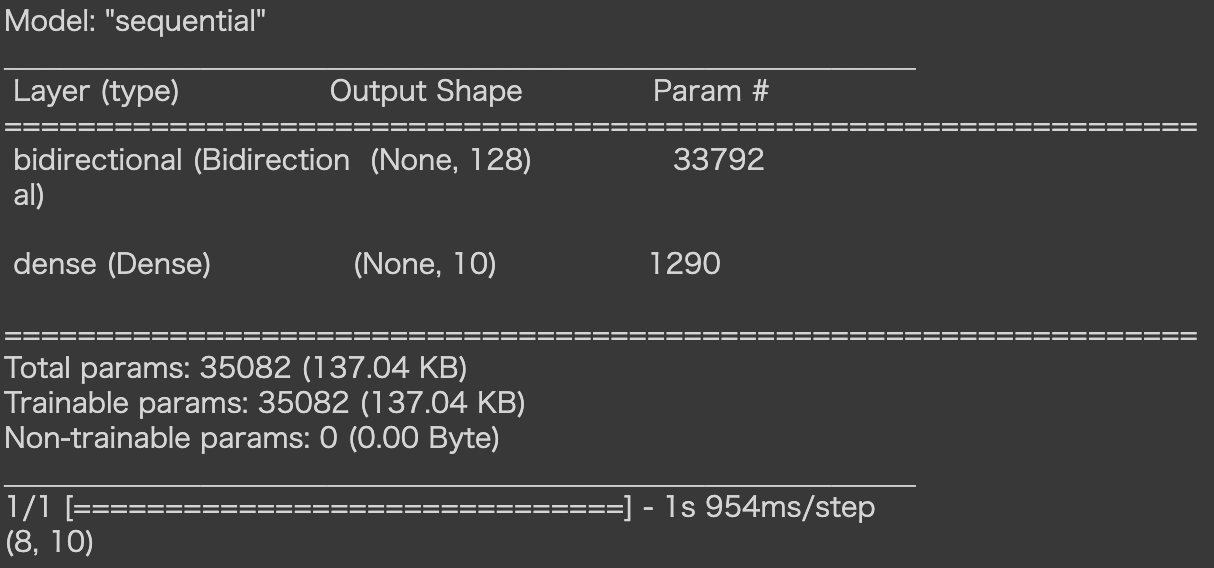
model_4.add(layers.Bidirectional(layers.LSTM(64)))
model_4.add(layers.Dense(10, activation='softmax'))

model_4.summary()
model_4.predict(sample[0]).shape

model_4.compile(
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    optimizer=tf.keras.optimizers.Adam(),
    metrics=['accuracy']
)

model_4.fit(
    dataset_prep_train,
    validation_data=dataset_prep_valid,
)

・勾配クリッピング

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers

tf.keras.backend.clear_session()
model_5 = tf.keras.models.Sequential()
model_5.add(layers.Input((NUM_DATA_POINTS, 1)))
model_5.add(layers.LSTM(64))
model_5.add(layers.Dense(10, activation='softmax'))

model_5.summary()
model_5.predict(sample[0]).shape

model_5.compile(
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    optimizer=tf.keras.optimizers.Adam(clipvalue=0.5),
    metrics=['accuracy']
)

model_5.fit(
    dataset_prep_train,
    validation_data=dataset_prep_valid,
)

確認テスト

なし

[フレームワーク演習] Seq2Seq

・Encoder-Decoderモデルの一種。Seq2Seqの課題は一問一答しかできないことであり、問いに対して文脈も何もなく、ただ応答が行われ続ける。

実装演習キャプチャ

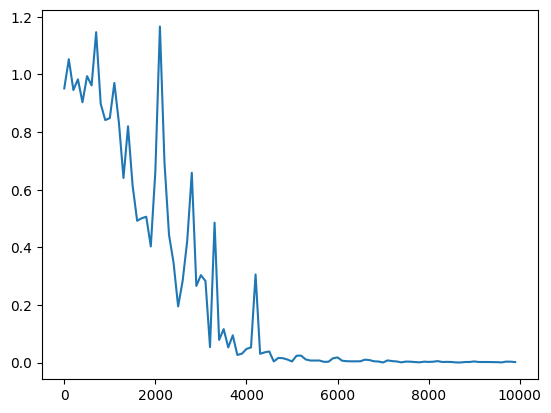
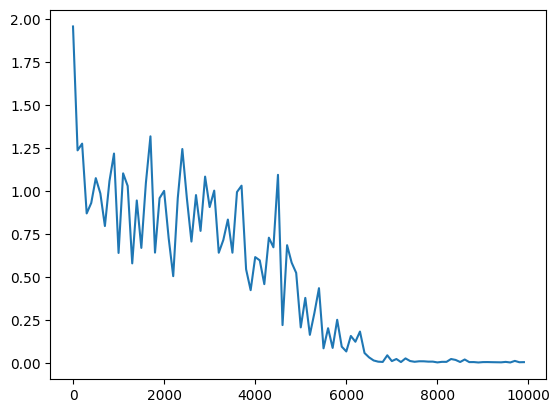
・Seq2Seq(Encoder-Decoder)モデルを用いたsin-cosの変換

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# データの準備
x = np.linspace(-3 * np.pi, 3 * np.pi, 100)
seq_in = np.sin(x)
seq_out = np.cos(x)

# NUM_ENC_TOKENS: 入力データの次元数
# NUM_DEC_TOKENS: 出力データの次元数
# NUM_HIDDEN_PARAMS: 単純RNN層の出力次元数(コンテキストの次元数にもなる)
# NUM_STEPS: モデルへ入力するデータの時間的なステップ数。

NUM_ENC_TOKENS = 1
NUM_DEC_TOKENS = 1
NUM_HIDDEN_PARAMS = 10
NUM_STEPS = 24

# 学習を行うためのモデルを定義
tf.keras.backend.clear_session()

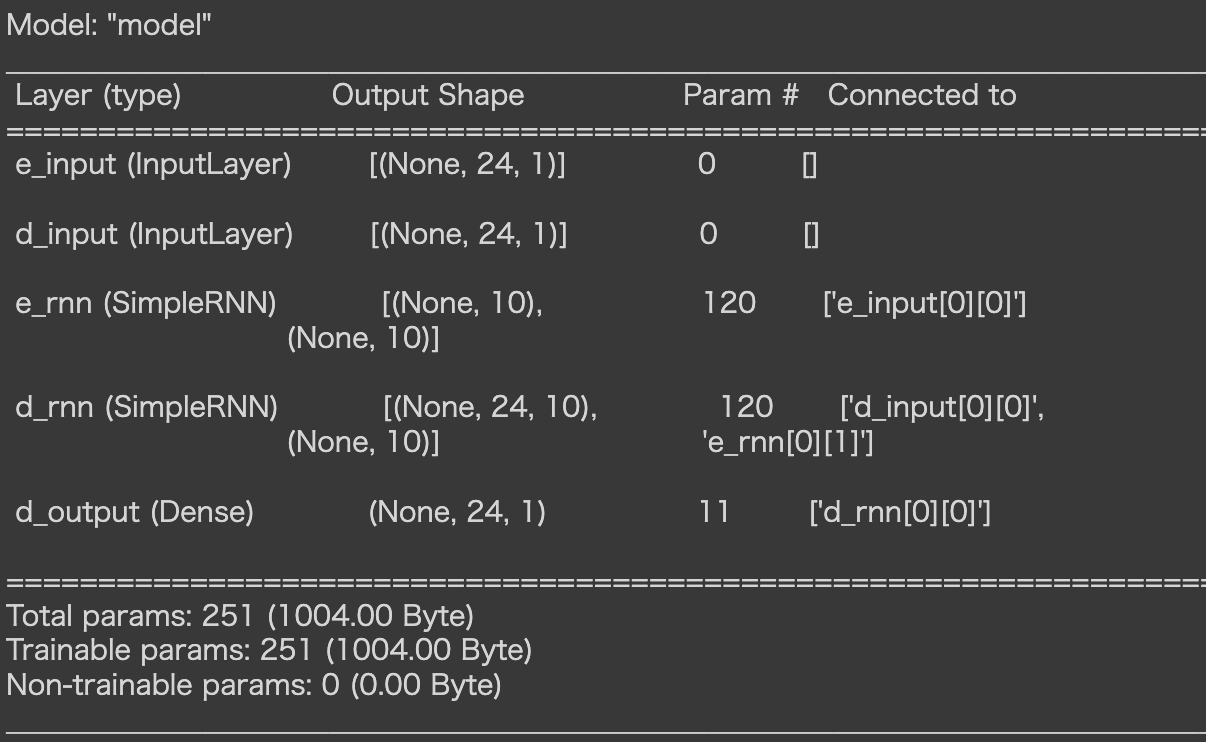
e_input = tf.keras.layers.Input(shape=(NUM_STEPS, NUM_ENC_TOKENS), name='e_input')
_, e_state = tf.keras.layers.SimpleRNN(NUM_HIDDEN_PARAMS, return_state=True, name='e_rnn')(e_input)

d_input = tf.keras.layers.Input(shape=(NUM_STEPS, NUM_DEC_TOKENS), name='d_input')
d_rnn = tf.keras.layers.SimpleRNN(NUM_HIDDEN_PARAMS, return_sequences=True, return_state=True, name='d_rnn')
d_rnn_out, _ = d_rnn(d_input, initial_state=[e_state])

d_dense = tf.keras.layers.Dense(NUM_DEC_TOKENS, activation='linear', name='d_output')
d_output = d_dense(d_rnn_out)

model_train = tf.keras.models.Model(inputs=[e_input, d_input], outputs=d_output)
model_train.compile(optimizer='adam', loss='mean_squared_error')

model_train.summary()

# モデルの定義に合わせて学習用データを準備
# ex: エンコーダーの入力として使用する値。
# dx: デコーダーの入力として渡す値。最終的に出力したい値の1つ前のステップの値。
# dy: 最終的に推論したい値。dxと比べて時間的に1ステップ先の値となっている。

n = len(x) - NUM_STEPS
ex = np.zeros((n, NUM_STEPS))
dx = np.zeros((n, NUM_STEPS))
dy = np.zeros((n, NUM_STEPS))

for i in range(0, n):
  ex[i] = seq_in[i:i + NUM_STEPS]
  dx[i, 1:] = seq_out[i:i + NUM_STEPS - 1]
  dy[i] = seq_out[i: i + NUM_STEPS]

ex = ex.reshape(n, NUM_STEPS, 1)
dx = dx.reshape(n, NUM_STEPS, 1)
dy = dy.reshape(n, NUM_STEPS, 1)

# 学習を行う
BATCH_SIZE = 16
EPOCHS = 80

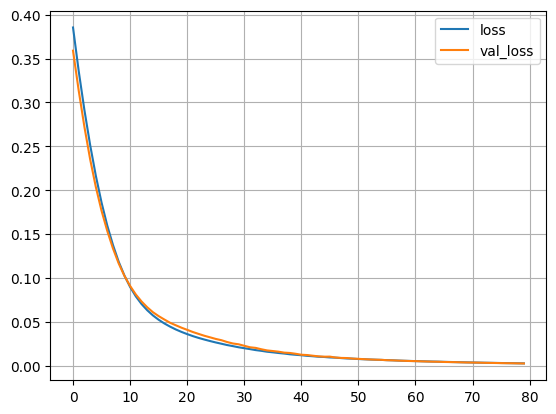
history = model_train.fit([ex, dx], dy, batch_size=BATCH_SIZE, epochs=EPOCHS, validation_split=0.2, verbose=False)

# 学習の進行状況をグラフに描画
loss = history.history['loss']
plt.plot(np.arange(len(loss)), loss, label='loss')

loss = history.history['val_loss']
plt.plot(np.arange(len(loss)), loss, label='val_loss')

plt.grid()
plt.legend()
plt.show()

# 推論を行うためのモデルを構築
model_pred_e = tf.keras.models.Model(inputs=[e_input], outputs=[e_state])

pred_d_input = tf.keras.layers.Input(shape=(1, 1))
pred_d_state_in = tf.keras.layers.Input(shape=(NUM_HIDDEN_PARAMS))

pred_d_output, pred_d_state = d_rnn(pred_d_input, initial_state=[pred_d_state_in])
pred_d_output = d_dense(pred_d_output)


pred_d_model = tf.keras.Model(inputs=[pred_d_input, pred_d_state_in], outputs=[pred_d_output, pred_d_state])

# モデルの推論を行う関数を準備
def predict(input_data):
  state_value = model_pred_e.predict(input_data)
  _dy = np.zeros((1, 1, 1))
  
  output_data = []
  for i in range(0, NUM_STEPS):
    y_output, state_value = pred_d_model.predict([_dy, state_value])
    
    output_data.append(y_output[0, 0, 0])
    _dy[0, 0, 0] = y_output

  return output_data

# 推論の実行
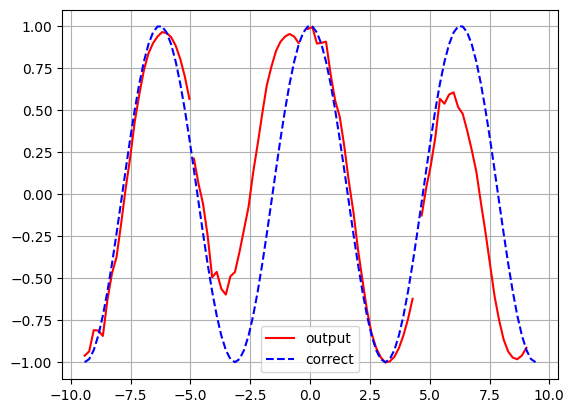
init_points = [0, 24, 49, 74]

for i in init_points:
  _x = ex[i : i + 1]
  _y = predict(_x)
    
  if i == 0:
    plt.plot(x[i : i + NUM_STEPS], _y, color="red", label='output')
  else:
    plt.plot(x[i : i + NUM_STEPS], _y, color="red")

plt.plot(x, seq_out, color = 'blue', linestyle = "dashed", label = 'correct')
plt.grid()
plt.legend()
plt.show() 

確認テスト

なし

[フレームワーク演習] data-augumentation

・data-augumentationとは、データを水増しする手法とのこと
・モデルがより多様なデータに適応できるようになり、過学習を防止できる
・反転、回転、平行移動、合成などを用いてデータを多数作成できる

実装演習キャプチャ

・データの水増しを実施

# TensorFlow等のライブラリをインポート
# 一部の処理でNumpyを使用して記述
import numpy as np
# データの水増し用APIを有するライブラリ
import tensorflow as tf
# 擬似乱数を生成するモジュール
import random
# 画像を表示するライブラリ
import matplotlib.pyplot as plt
# 画像をNotebook内に表示させるための指定
%matplotlib inline

# 画像を表示するshow_images関数を定義
def show_images(images):
    """複数の画像を表示する"""
    n = 1
    while n ** 2 < len(images):
        n += 1
    for i, image in enumerate(images):
        plt.subplot(n, n, i + 1)
        plt.imshow(image)
        plt.axis('off')
    plt.show()

#元画像（任意のJPEG形式画像）ファイルを取得
mkdir sample_data
wget -qnc --no-check-certificate -O ./sample_data/image_origin.jpg \
https://github.com/opencv/opencv/raw/master/samples/data/fruits.jpg

# 元画像を読み込む
contents = tf.io.read_file("./sample_data/image_origin.jpg")
image_origin = tf.image.decode_jpeg(contents, channels=3)

# 元画像を表示
image = image_origin
show_images([image.numpy()])

・元画像を表示

・Horizontal Flip：水平方向（左右）反転処理

image = image_origin
image = tf.image.random_flip_left_right(image, seed=123)

show_images([image.numpy()])

・Vertical Flip：垂直方向（上下）反転処理

image = image_origin
image = tf.image.random_flip_up_down(image, seed=123)

show_images([image.numpy()])

・Crop：あるサイズを画像中からランダムに切り出す処理

image = image_origin
image = tf.image.random_crop(image, size=(100, 100, 3), seed=123)

show_images([image.numpy()])

・Contrast：コントラストをランダムに調整する処理

image = image_origin
image = tf.image.random_contrast(image, lower=0.4, upper=0.6)

show_images([image.numpy()])

・Brightness：輝度値 𝛿 をランダムに調整する処理

image = image_origin
image = tf.image.random_brightness(image, max_delta=0.8)

show_images([image.numpy()])

・Hue：色相 𝛿 をランダムに調整する処理

image = image_origin
image = tf.image.random_hue(image, max_delta=0.1)

show_images([image.numpy()])

・Rotate：回転処理

image = image_origin
image = tf.image.rot90(image, k=1)

show_images([image.numpy()])

・複数の手法の組み合わせ

def data_augmentation(image):
    image = tf.image.random_flip_left_right(image)
    image = tf.image.random_flip_up_down(image)
    image = tf.image.random_contrast(image, lower=0.4, upper=0.6)
    image = tf.image.random_brightness(image, max_delta=0.8)
    image = tf.image.rot90(image, k=random.choice((0, 1, 2)))
    image = tf.image.random_hue(image, max_delta=0.1)
    return image

image = image_origin

show_images([data_augmentation(image).numpy() for _ in range(36)])

確認テスト

なし

[フレームワーク演習] activate_functions

・activate_functionsとは、活性化関数のこと
・ニューラルネットワークの順伝播（forward）では、線形変換で得た値に対して、非線形な変換を行う。非線形な変換を行う際に用いられる関数を、活性化関数という。
・中間層に用いる活性化関数：ステップ関数、シグモイド関数、tanh、ReLU、Leaky ReLU、Swish
・出力層に用いる活性化関数；シグモイド関数、ソフトマックス関数、恒等関数（活性化関数なし）

実装演習キャプチャ

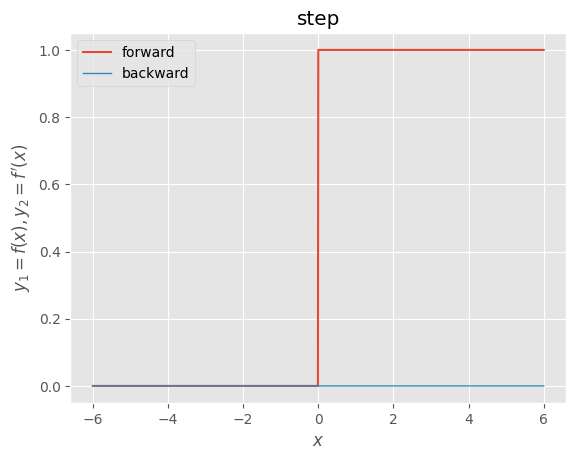
・ステップ関数

def step_function(x):
    """forward
       
       step
       ステップ関数
       (閾値0)
    """
    return np.where(x >= 0.0, 1.0, 0.0)

def d_step_function(x):
    """backward
       
       derivative of step
       ステップ関数の導関数
       (閾値0)
    """
    dx = np.where(x == 0.0, np.nan, 0.0)
    return dx

x = np.arange(-600, 601, 1) * 0.01
f, d, = step_function, d_step_function
y1, y2 = f(x), d(x)

_, ax = plt.subplots()
ax.plot(x, y1, label=f.__doc__.split("\n")[0].strip())
ax.plot(x, y2, label=d.__doc__.split("\n")[0].strip(), linewidth=1.0)
ax.set_xlabel("$x$")
ax.set_ylabel("$y_{1}=f(x), y_{2}=f^{\prime}(x)$")
ax.set_title(f.__doc__.split("\n")[2].strip())
ax.legend()

plt.show()

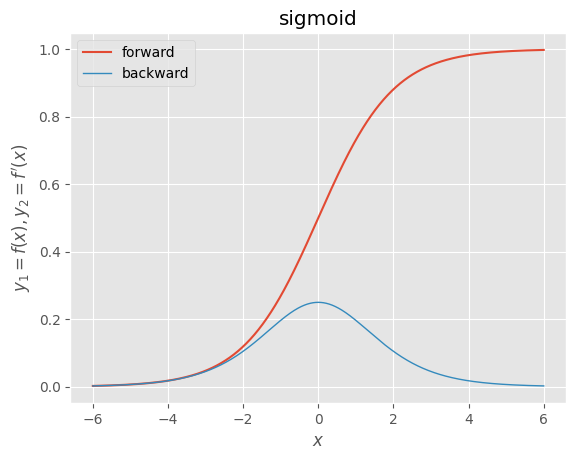
・シグモイド関数

ef sigmoid(x):
    """forward
       
       sigmoid
       シグモイド関数
    """
    return 1.0 / (1.0 + np.exp(-x))

def d_sigmoid(x):
    """backward
       
       derivative of sigmoid
       シグモイド関数の導関数
    """
    dx = sigmoid(x) * (1.0 - sigmoid(x))
    return dx

x = np.arange(-600, 601, 1) * 0.01
f, d = sigmoid, d_sigmoid
y1, y2 = f(x), d(x)

_, ax = plt.subplots()
ax.plot(x, y1, label=f.__doc__.split("\n")[0].strip())
ax.plot(x, y2, label=d.__doc__.split("\n")[0].strip(), linewidth=1.0)
ax.set_xlabel("$x$")
ax.set_ylabel("$y_{1}=f(x), y_{2}=f^{\prime}(x)$")
ax.set_title(f.__doc__.split("\n")[2].strip())
ax.legend()

plt.show()

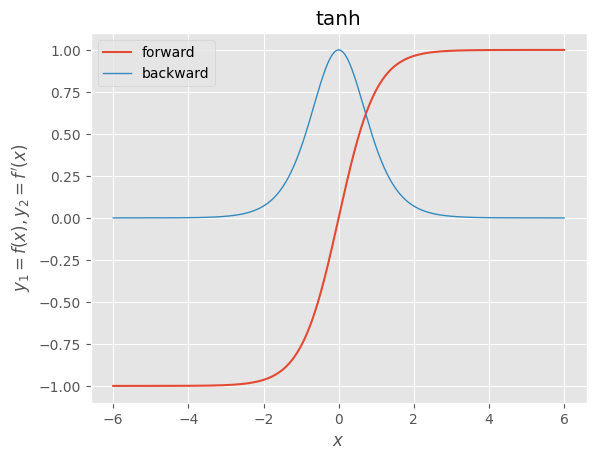
・tanh

def tanh(x):
    """forward
       
       tanh
       双曲線正接関数
       (1)
    """
    return np.tanh(x)

def d_tanh(x):
    """backward
       
       derivative of tanh
       双曲線正接関数の導関数
       (1)
    """
    dx = 1.0 / np.square(np.cosh(x))
    return dx

x = np.arange(-600, 601, 1) * 0.01
f, d = tanh, d_tanh
y1, y2 = f(x), d(x)

_, ax = plt.subplots()
ax.plot(x, y1, label=f.__doc__.split("\n")[0].strip())
ax.plot(x, y2, label=d.__doc__.split("\n")[0].strip(), linewidth=1.0)
ax.set_xlabel("$x$")
ax.set_ylabel("$y_{1}=f(x), y_{2}=f^{\prime}(x)$")
ax.set_title(f.__doc__.split("\n")[2].strip())
ax.legend()

plt.show()

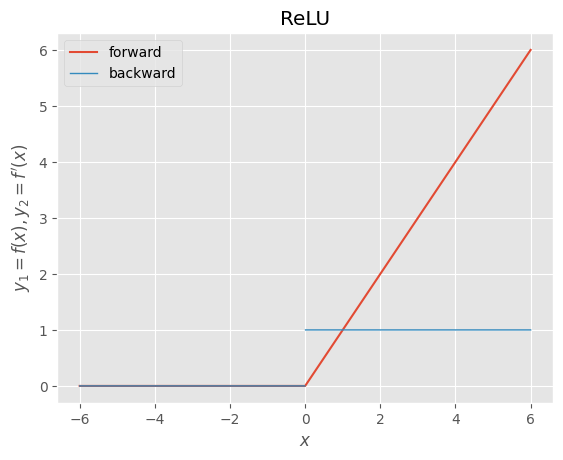
・ReLU

def relu(x):
    """forward
       
       ReLU
       正規化線形関数
    """
    return np.maximum(0, x)

def d_relu(x):
    """backward
       
       derivative of ReLU
       正規化線形関数の導関数
    """
    dx = np.where(x > 0.0, 1.0, np.where(x < 0.0, 0.0, np.nan))
    return dx

x = np.arange(-600, 601, 1) * 0.01
f, d = relu, d_relu
y1, y2 = f(x), d(x)

_, ax = plt.subplots()
ax.plot(x, y1, label=f.__doc__.split("\n")[0].strip())
ax.plot(x, y2, label=d.__doc__.split("\n")[0].strip(), linewidth=1.0)
ax.set_xlabel("$x$")
ax.set_ylabel("$y_{1}=f(x), y_{2}=f^{\prime}(x)$")
ax.set_title(f.__doc__.split("\n")[2].strip())
ax.legend()

plt.show()

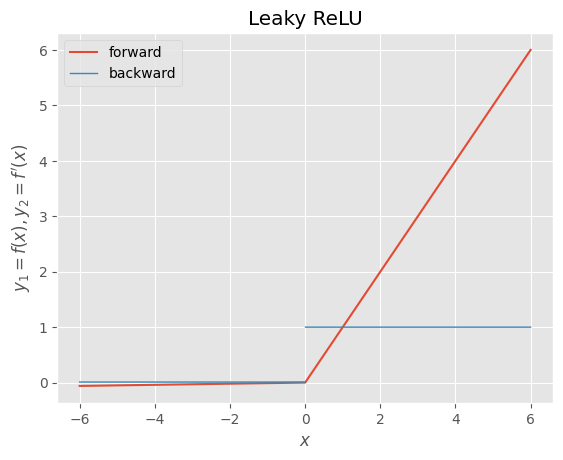
・Leaky ReLU

alpha = 0.01

def lrelu(x):
    """forward
       
       Leaky ReLU
       漏洩正規化線形関数
    """
    return np.maximum(alpha*x, x)

def d_lrelu(x):
    """backward
       
       derivative of Leaky ReLU
       漏洩正規化線形関数の導関数
    """
    dx = np.where(x > 0.0, 1.0, np.where(x < 0.0, alpha, np.nan))
    return dx

x = np.arange(-600, 601, 1) * 0.01
f, d = lrelu, d_lrelu
y1, y2 = f(x), d(x)

_, ax = plt.subplots()
ax.plot(x, y1, label=f.__doc__.split("\n")[0].strip())
ax.plot(x, y2, label=d.__doc__.split("\n")[0].strip(), linewidth=1.0)
ax.set_xlabel("$x$")
ax.set_ylabel("$y_{1}=f(x), y_{2}=f^{\prime}(x)$")
ax.set_title(f.__doc__.split("\n")[2].strip())
ax.legend()

plt.show()

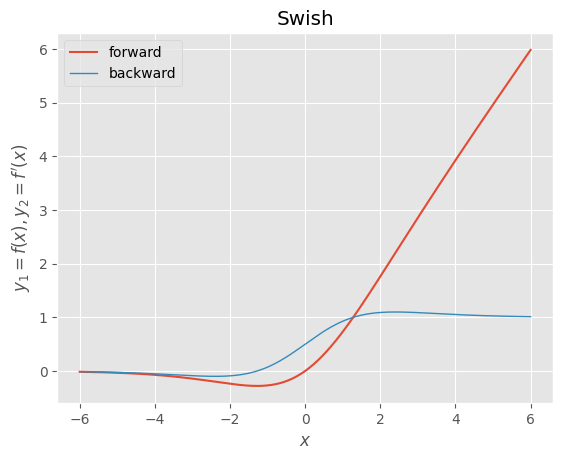
・Swish

beta = 1.0

def swish(x):
    """forward
       
       Swish
       シグモイド加重線形関数
    """
    return x * sigmoid(beta*x)

def d_swish(x):
    """backward
       
       derivative of Swish
       シグモイド加重線形関数の導関数
    """
    dx = beta*swish(x) + sigmoid(beta*x)*(1.0 - beta*swish(x)) 
    return dx

x = np.arange(-600, 601, 1) * 0.01
f, d = swish, d_swish
y1, y2 = f(x), d(x)

_, ax = plt.subplots()
ax.plot(x, y1, label=f.__doc__.split("\n")[0].strip())
ax.plot(x, y2, label=d.__doc__.split("\n")[0].strip(), linewidth=1.0)
ax.set_xlabel("$x$")
ax.set_ylabel("$y_{1}=f(x), y_{2}=f^{\prime}(x)$")
ax.set_title(f.__doc__.split("\n")[2].strip())
ax.legend()

plt.show()

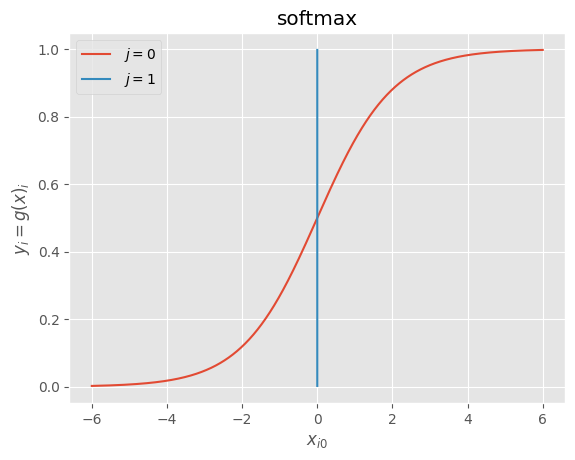
・多値分類: ソフトマックス関数

def softmax(x):
    """forward
       
       softmax
       ソフトマックス関数
    """
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x)  # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x))

def d_softmax(x):
    """backward
       
       derivative of softmax
       ソフトマックス関数の導関数
    """
    y = softmax(x)
    dx = -y[:,:,None] * y[:,None,:]       # ヤコビ行列を計算 (i≠jの場合)
    iy, ix = np.diag_indices_from(dx[0])  # 対角要素の添字を取得
    dx[:,iy,ix] = y * (1.0 - y)           # 対角要素値を修正 (i＝jの場合)
    return dx

x = np.pad(np.arange(-600, 601, 1).reshape((-1, 1)) * 0.01, ((0, 0), (0, 1)), 'constant')
g = softmax
y = g(x)

_, ax = plt.subplots()
for j in range(x.shape[1]):
    ax.plot(x[:,j], y[:,j], label=r" $j={}$".format(j))
ax.set_xlabel("$x_{i0}$")
ax.set_ylabel("$y_{i}=g(x)_{i}$")
ax.set_title(g.__doc__.split("\n")[2].strip())
ax.legend()

plt.show()

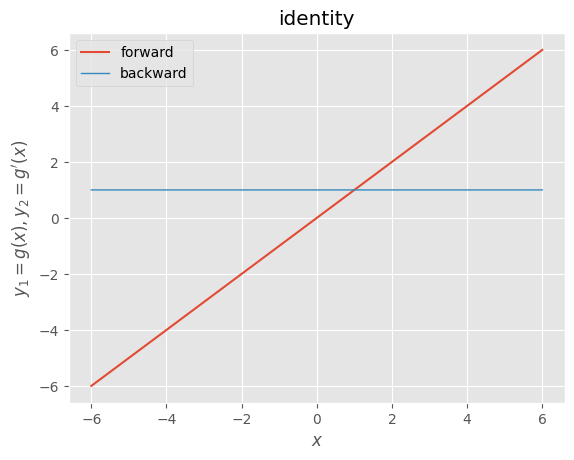
・回帰: 恒等関数 (活性化関数なし)

def identity(x):
    """forward
       
       identity
       恒等関数
    """
    return x

def d_identity(x):
    """backward
       
       derivative of identity
       恒等関数の導関数
    """
    dx = np.ones_like(x)
    return dx

x = np.arange(-600, 601, 1) * 0.01
g, d = identity, d_identity
y1, y2 = g(x), d(x)

_, ax = plt.subplots()
ax.plot(x, y1, label=g.__doc__.split("\n")[0].strip())
ax.plot(x, y2, label=d.__doc__.split("\n")[0].strip(), linewidth=1.0)
ax.set_xlabel("$x$")
ax.set_ylabel("$y_{1}=g(x), y_{2}=g^{\prime}(x)$")
ax.set_title(g.__doc__.split("\n")[2].strip())
ax.legend()

plt.show()

確認テスト

なし