はじめに
論文リンク: https://arxiv.org/pdf/1703.06114.pdf
集合を入力として扱えるフレームワークを提案したNIPS2017の論文
集合ごとに出力が決まるということは,入力要素の並べ替えに左右されないということ.
この論文では大きく2つのモデルを提案している.
- permutation invariant model: 入力集合の順番を変えても同じ出力
- permutation equivariant model: 入力集合に1対1対応する集合を出力
※ permutation: (集合の)置換,要素を並び替えること
※ invarinat: 不変
※ equivarint: 同変
モチベーション: 順不同の結果が欲しい
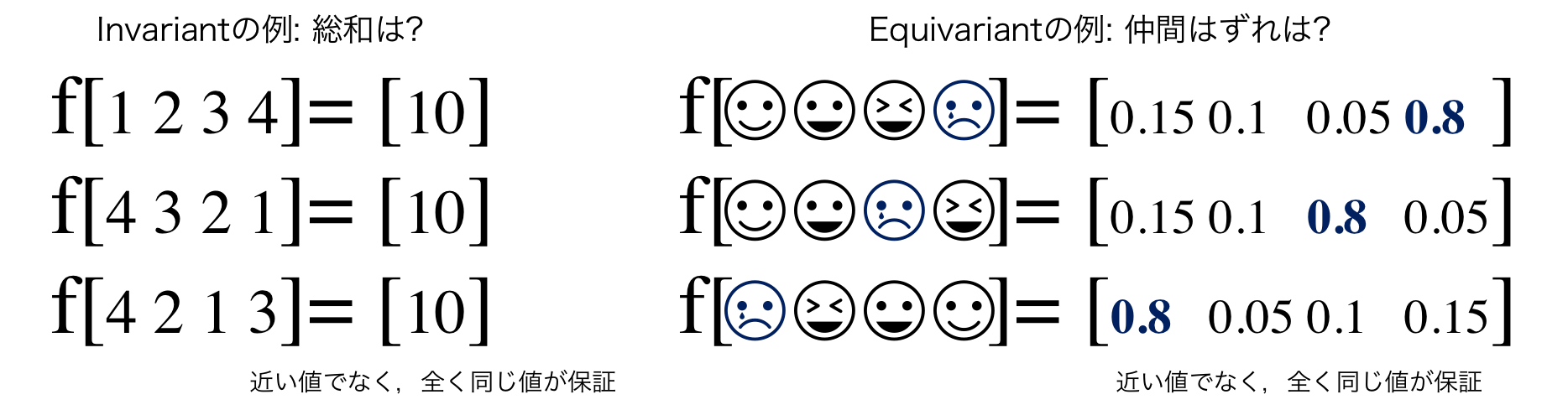
普通のMLPを使えば,要素を入れ替えたら出力結果はもちろん変わる.例えばRNNなら,入力をシーケンスとして1要素ずつ処理して,内部状態を更新していくことで学習できるかもしれない.しかし,要素の並べ替えに対して同じ結果は保証されない.1 2 3 4で読み込んだ際の演算結果が10.00001で4 3 2 1で読み込んだ演算結果が9.99999かもしれない.
この論文では要素の並べ替えに対して,出力結果が全く同じになることが保証されたモデルを作ろうとしている.
Permutation invariant
permutation invariant,つまり入力の要素を自由に交換しても出力が同じになるモデル.
やりたいことは,ある入力$\textbf x$と置換$\pi$に対して,$\textrm f(\pi \textbf{x})=\textrm f(\textbf{x})$.
Invarinat model:
入力集合$\textrm X$の各要素が可算集合に属するとき,出力$\textrm{f(X)}$が適当な関数$\phi (\cdot),\rho(\cdot)$を使って以下の式で示せれば,関数$\textrm{f}(\cdot)$はinvariant model. (※ 証明は論文内AppendixA参照)
f(X)={\rho}\left({\sum}_{x\in X}\phi(x)\right)
※ $\mathrm X$の各要素が$\mathbb R$などの非可算集合に属する場合,固定サイズでしか不変を示せない.
図示すると...
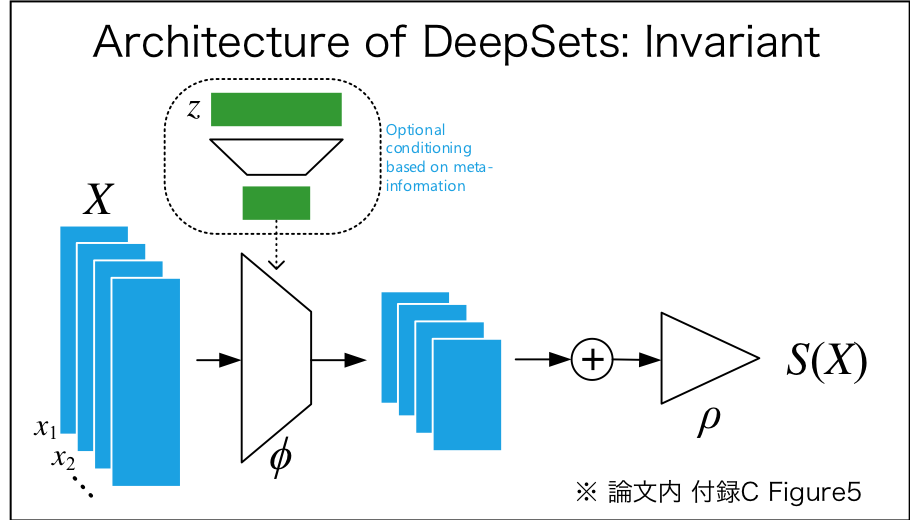
図のように条件付き写像も可能,メタ情報を$z$とすると$\phi(x_m)$のとこが$\phi(x_m|z)$になる.
Permutation equivariant
集合を入力して,各要素に1対1対応する集合を出力するモデル.要は全単射.
やりたいことは,ある入力$\textbf x$と置換$\pi$に対して,$\textbf f(\pi \textbf{x})=\pi \textbf f(\textbf{x})$.
Equivariant model (各要素が実数の場合):
[注意] 以下はニューラルネットワーク限定の話
サイズ$\textrm M$の実数の集合を入力として,サイズ$\textrm M$の実数の集合を出力するときを考える
($\mathbb{R^\mathrm{M} \rightarrow R^\mathrm{M}}$).モデルを以下のように表現する.
\textbf{f} (\textbf{x})=\sigma(\Theta\textbf{x})
※ ここで$\Theta$は重み(線形演算),$\sigma$は活性化関数(非線形演算)
このとき,重み行列$\Theta$が以下を満たすと,$\textbf f(\cdot)$はequivariant model.
\Theta=\lambda\textbf{I}+\gamma(\textbf{11}^\textrm{T})\\
\lambda,\gamma\in\mathbb{R}\;\;\;\;\;
\textbf{1}=[1,..., 1]^\textrm{T}\in\mathbb{R}^\textrm{M}\;\;\;\;\;
\textbf{I}\in\mathbb{R}^{\textrm{M}\times\textrm{M}}
$\textbf{I}$は単位行列.めんどく見えるけど,要は対角成分,非対角成分の全要素がそれぞれ同じ値.
つまり関数$\textbf{f}$は入力$\textbf{Ix}$と入力の総和$(\textbf{11}^\textrm{T})\textbf x$で構成される層.総和$(\textbf{11}^\textrm{T})\textbf x$は順番に依存しないので,permutation equivariant. (※ 証明は論文内AppendixB参照)
図示するとそりゃそうかとなる.
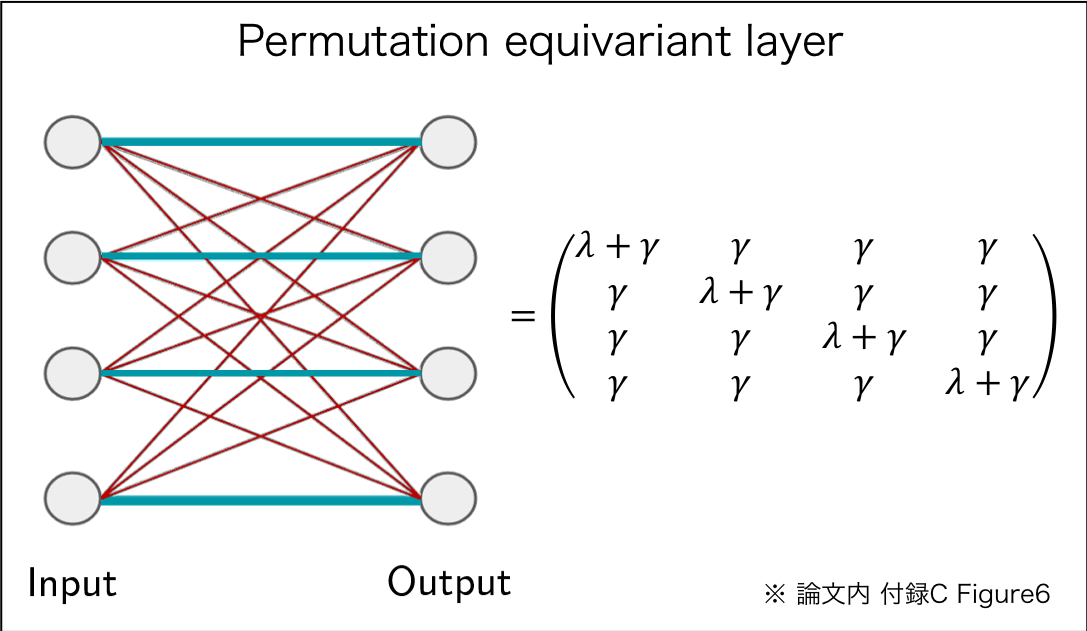
総和$(\textbf{11}^\textrm{T})\textbf x$でなくても置換不変ならOK.別のequivariant modelとしてmaxpoolingを使った以下の式も提案している.
\textbf{f}(\textbf{x})=\sigma(\lambda \textbf{Ix}+\gamma\ \textrm{maxpool}\textbf{(x)1})
いくつかのタスクでは上記のモデルの方がパフォーマンスが向上したらしい.
Equivariant model (マルチチャネル)
入力集合$\textbf x$の各要素が$\textrm D$チャネル,出力集合$\textbf y$の各要素が$\textrm {D}'$チャネルだとする,つまり
$\mathbb{R}^{\textrm{M}\times\textrm{D}}\rightarrow\mathbb{R}^{\textrm{M}\times\textrm{D'}}$.このときequivariant model $\textbf{f}(\cdot)$は行列演算を使って以下のような式で表せる.
\textbf{f}(\textbf{x})=\sigma(\textbf x\boldsymbol\Lambda-\textbf{11}^{\textrm T}\textbf x\boldsymbol\Gamma)\\
\boldsymbol\Lambda,\boldsymbol\Gamma\in\mathbb R^{\textrm{D}\times\textrm{D'}}
$\boldsymbol\Lambda,\boldsymbol\Gamma$が前述$\mathbb{R^\mathrm{M} \rightarrow R^\mathrm{M}}$のときのパラメータ$\lambda,\gamma$を"入力チャネル数$\times$出力チャネル数"だけ用意した行列になる.同様にmaxpoolingを使った式は,
\textbf{f}(\textbf{x})=\sigma(\textbf x\boldsymbol\Lambda-\textbf{1}\textrm{maxpool}(\textbf x)\boldsymbol\Gamma)
ここでの$\textrm{maxpool}(\textbf x)$はチャネルごとに最大値をとっているので$\in\mathbb R^{1\times\textrm{D}}$である.
図示すると...
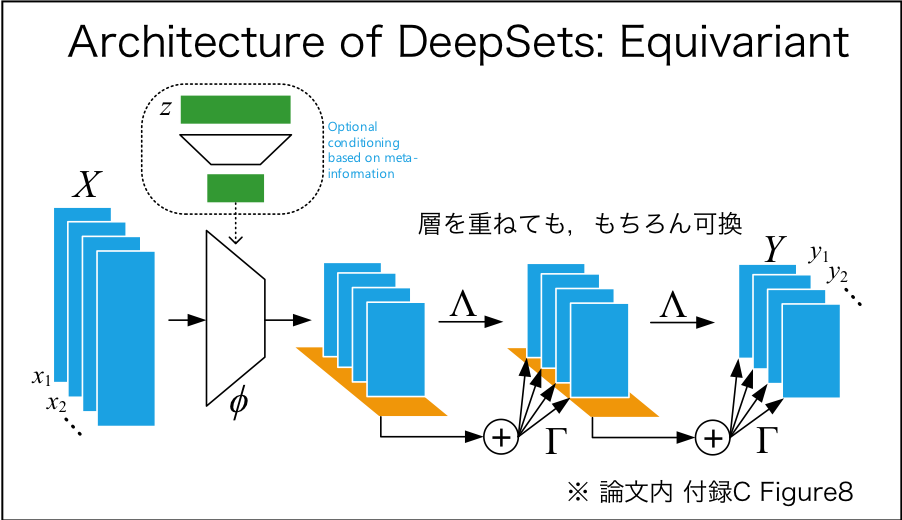
図のように層を重ねて使用してOK.
実験
1.Supervised Learning: Learning to Estimate Population Statistics
下図4つの指標で生成したガウス分布に従うサンプルを用意して,エントロピーや相互情報量を推定させるタスク. Support Distribution Machines(SDM)と比較.
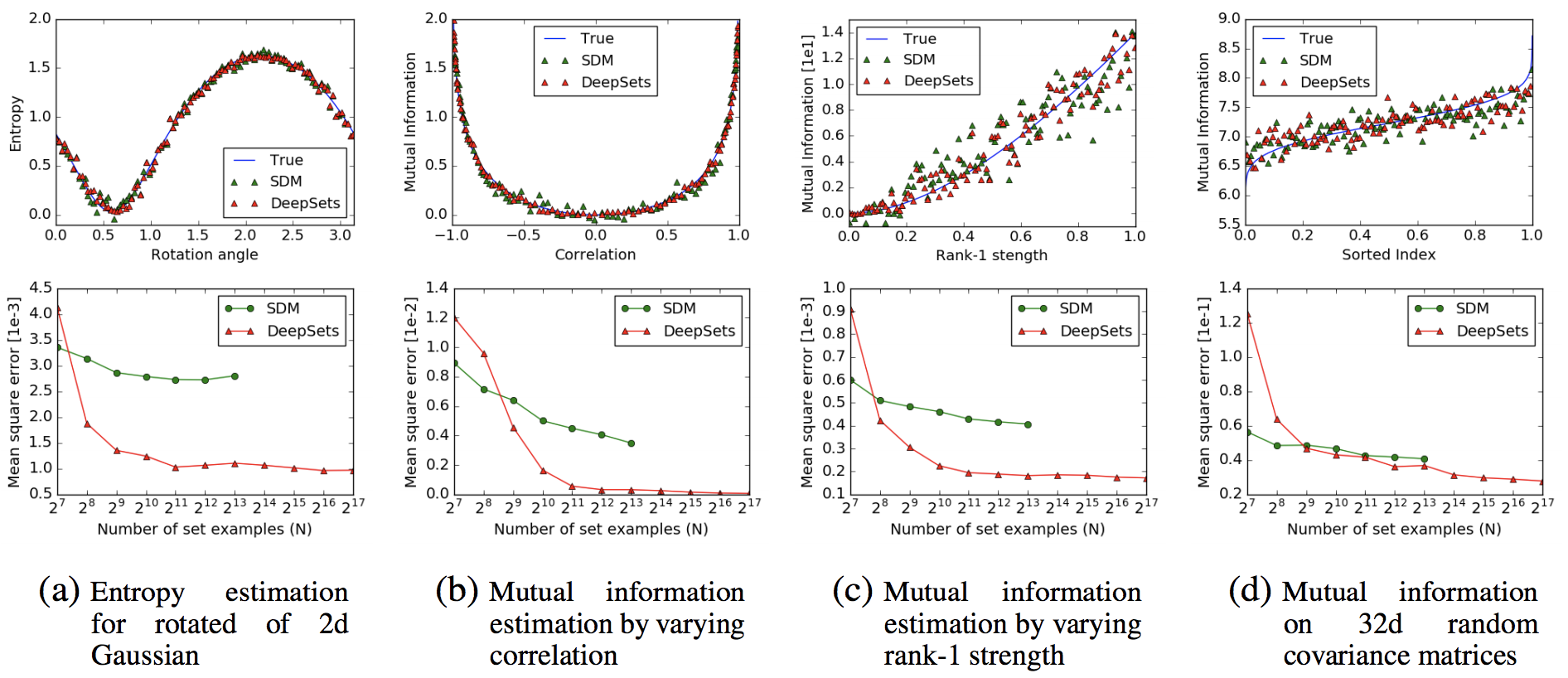
2.Sum of Digits
数字の総和を推定するタスク.学習時には要素数は10以下までとし,推定時は100以下.LSTM,GRUと比較.要素数が増えても精度の減少幅が低いのが強み.
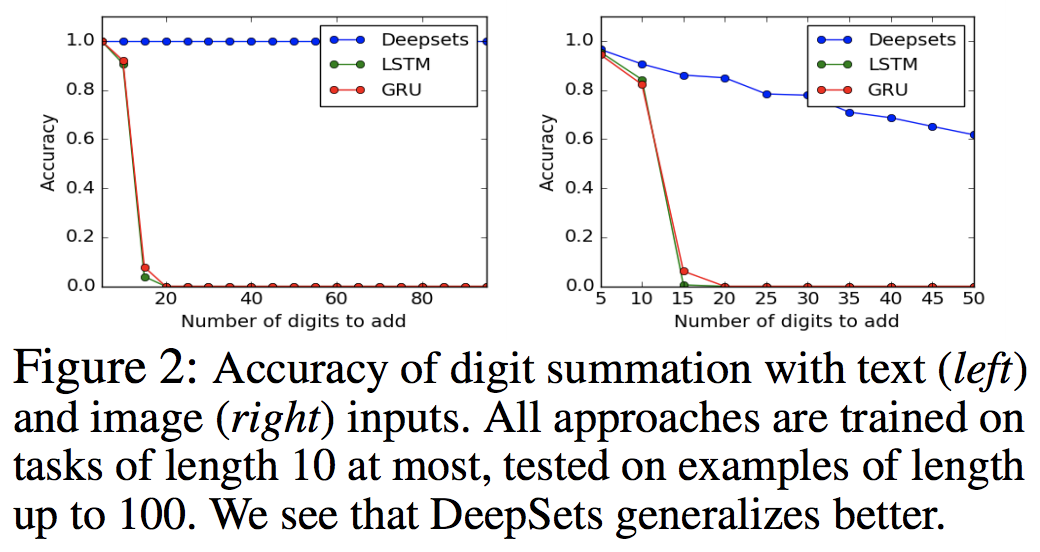
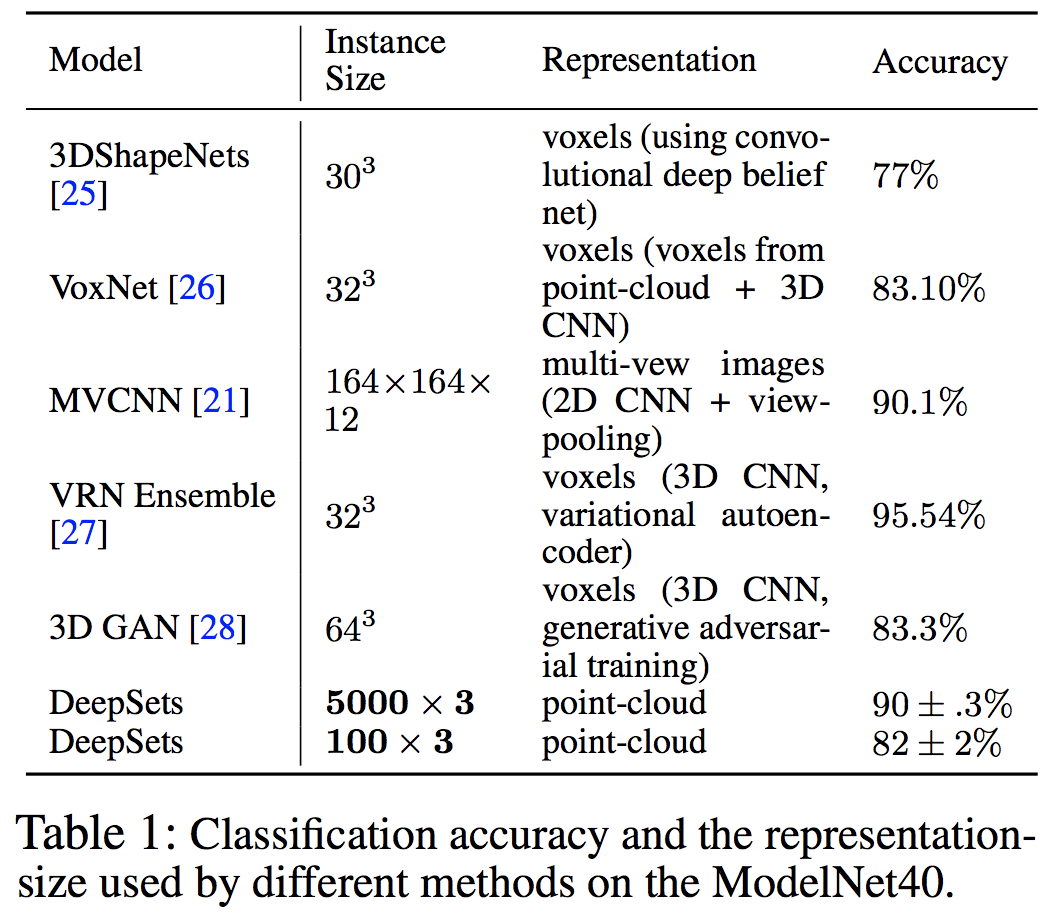
3.Point Cloud Classification
点群(xyz,3次元ベクトルの集合)データからのクラス分類(40クラス)タスク.インスタンスサイズ(点群の数)を100,1000,5000の3パターンで学習.他手法より少ないサイズで推定可能.
4.Improved Red-shift Estimation Using Clustering Information
各銀河クラスターを集合として,測光データから銀河の赤方偏移を推定するタスク.average scatterで評価.低い方がいい.

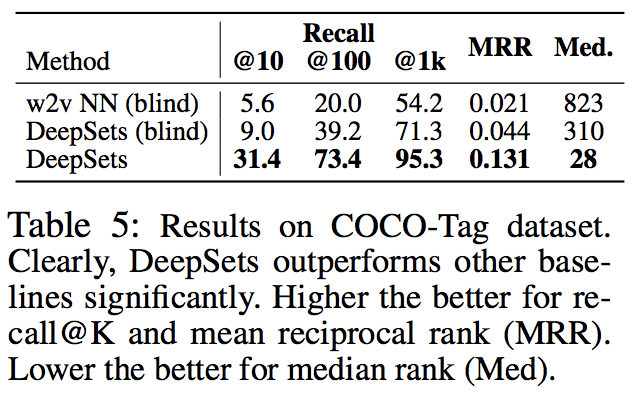
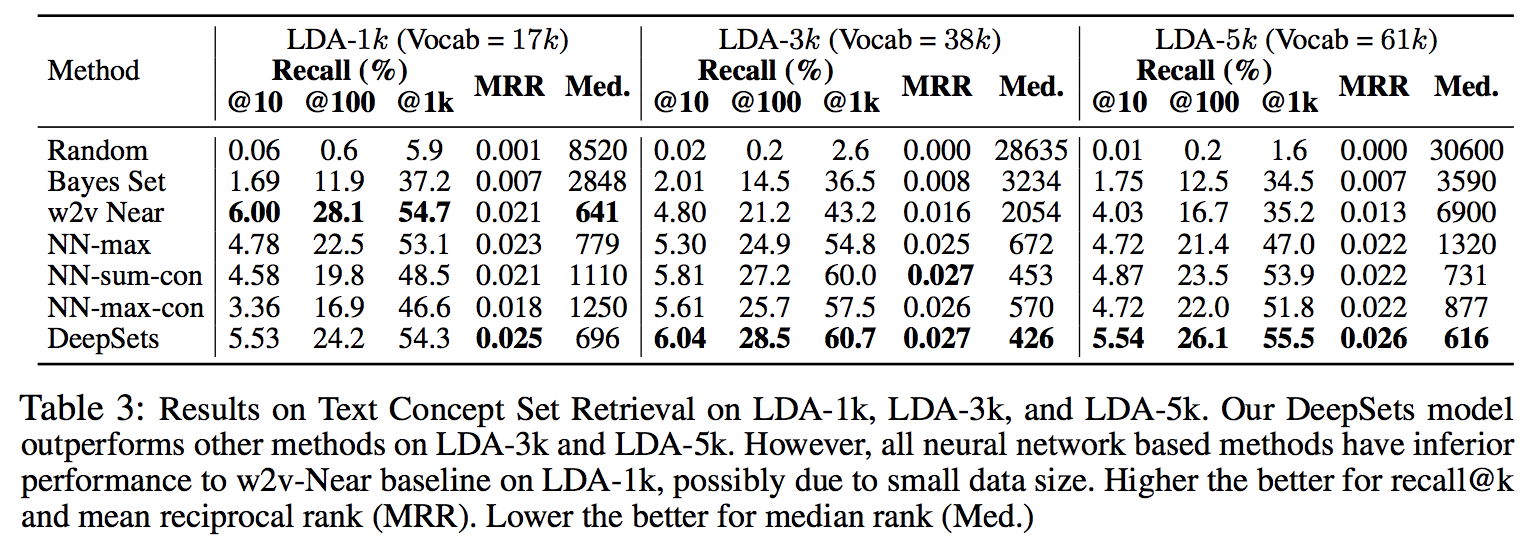
5.Text Concept Set Retrieval
単語のセットが与えられたら,似た単語を検索するタスク.表のVocabはvocabulary size.LDA-1kでにおいて10億語のコーパスで訓練されているw2v-Nearに勝てなかった.
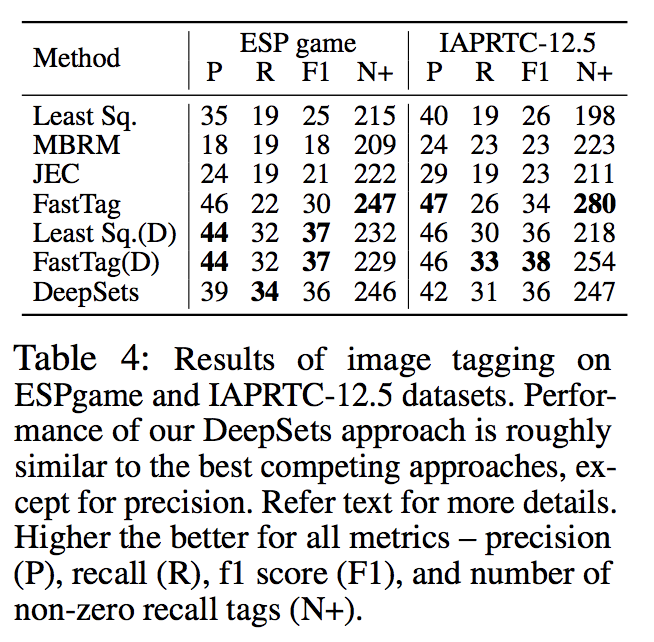
6.Image Tagging
7.Set Anomaly Detection
16枚の顔画像のうち,仲間はずれを見つけるタスク.equivariant layerを全結合層に置き換えると精度75%から6%になった.

最後に
自分は手法と実験しか読んでないので(他は理解できないので),関連研究,証明等気になる方は...
論文リンク: https://arxiv.org/pdf/1703.06114.pdf