これは株式会社TimeTree Advent Calendar 2023の16日目の記事です。
こんにちは。TimeTree の iOS エンジニア @Bax です。
TimeTree はプレミアム(有料プラン)でいくつかの機能を提供しています。その1つにバーチカルカレンダーがあります。こちらは私が過去に開発を担当していたもので、その開発のあれこれについて書きたいと思います。
バーチカルカレンダーとは何か
月ごとに表示されるカレンダーを私たちはマンスリーカレンダーと呼んでいます。一方で、バーチカルカレンダーは時間軸で1日の予定を見ることができるカレンダーです。あまり馴染みのない言葉かもしれませんが、テレビ番組表のようなタイムテーブルに近いものです。
| マンスリーカレンダー | バーチカルカレンダー |
|---|---|

|

|
当初、バーチカルカレンダーはユーザーさんから多くの実装要望をいただいていた機能の1つです。正直なところ、開発を担当することが決まった時はマンスリーよりは簡単だろうと甘く見ていた部分がありました(笑)ところが開発を進めていくうちに難問が立ちはだかることになります。
※マンスリーの難しさについては @fujikky が前日に書いてくれました。こちらも参照ください🙏
描画方法と最適化について
バーチカルカレンダーは、下地となる罫線とその上に複数の予定を描画することから成り立ちます。このような複数のビューを描画するケースでは Core Graphics でおこなうよりも SwiftUI で実装する方が比較的簡単にできます。罫線は1時間を単位として24時間分が描画され、予定はその開始時間と終了時間を基準に罫線上の座標に描画されます。
var body: some View {
ZStack {
VStack(spacing: 0) {
ForEach(0 ..< 24) { index in
RuledLine(forHour: index)
}
}
ForEach(events, id: \.self) { event in
EventView(event: event)
.frame(width: event.width, height: event.height)
.position(event.position)
}
}
}
ところで、時間の重なった予定についてはどのように描画する必要があるでしょうか?時間の重なりはうまく1列では表現できないので、2列の表示になります。さらに重なった予定があった場合は3列、4列と増えていくことになります。
| 1列 | 2列 |
|---|---|

|

|
しかし、困ったことに3列以上になると複数の表示パターンが考えられます。以下のケースでは明らかに左のビューより右のビューの表示が期待されていることが分かると思います。この場合はまだ想像が付きますが、もしそれ以上の予定が存在した場合はどうでしょうか。
| 3列(パターン1) | 3列(パターン2) |
|---|---|

|

|
1日の予定登録数に制限はないため、無数のパターンに対して表示の最適化をおこなっていく必要があります。この最適化を言語化すれば、「予定同士を重ねず、列が最小となるように隙間を少なく描画すること」がバーチカルカレンダーを開発する上での課題となります。ようやく取り組むべきコアな課題に気がつきました。
定式化
課題を言語化できたものの、それを定式化してプログラミングすることはなかなか難しいものです。単純な例だと簡単に想像ができたのですが、一般化しようとするとこれはダメだとなり幾度も立ち戻りました。まず一番最初に思いついたのは、1分ごとに区切られたマスを用意し、できるだけ列の少なくなる並びを探す方法です。
予定数nより列は大きくならないはずなので、1日分のデータ
24 * 60 * n
のマスを持つ2次元空間を用意し、予定が存在するマスは 0 存在しないマスは 1 を埋めます。この中で並び替えを行うことで、できるだけ少ない列数のパターンを探します。
これは当然ですが、メモリ、計算時間ともに効率的とは言えませんので別の方法を考えることになりました。
予定の重なりについて
カレンダー開発において、予定が時間的に重なっているかどうかは有名な式で表されます。予定aの開始時間を a.startDate 終了時間を a.endDate とすると、予定a、予定bが重なっているかどうかは以下の式で表されます。
let isOverlapped = (b.startDate <= a.endDate) && (a.startDate <= b.endDate)
慣れていないと、違う者同士の startDate と endDate を比較していることが気持ち悪く感じるのですが、2つがどのような位置関係にあっても条件式が正しいことが分かると思います。
描画に必要な列の最小値
複雑に重なり合っている予定がいくつもある場合、最も重なりが大きい部分に着目することによって、描画に必要な列の最小値を求めることが可能です。これを効率的に調べるのに有名なアルゴリズムがありました。実行時間の決まったタスクを CPU で並列に実行する場合、その最大同時実行タスク数はいくつになるかを求めるものです。
例えば上記のページにある5つのタスク (0,2), (3, 7), (4,6), (7,8), (1,5) が与えられた場合、同時実行タスクは (4, 5) の間で最も多くなり、その数は 3 という結果は、バーチカルカレンダーでは以下のような結果に置き換えることができます。
- 0時〜2時、3時〜7時、4時〜6時、7時〜8時、1時〜5時にそれぞれ5つの予定がある
- 4〜5時の間が最も予定同士の重なりが大きい
- 描画に必要な列の最小値は 3
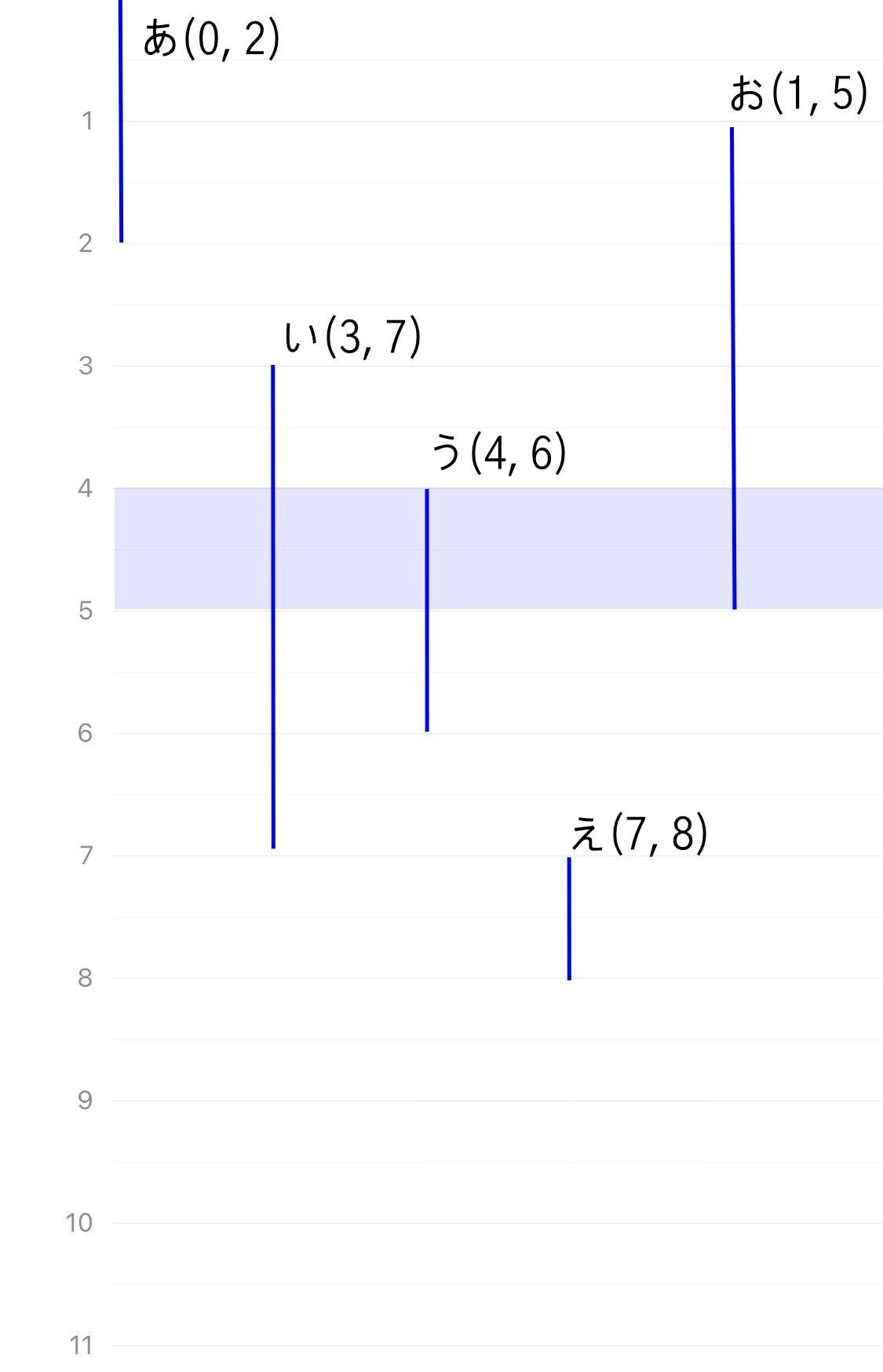
この結論を得た時はかなり疑わしかったです。まさかバーチカルの配置問題が CPU の最大同時実行タスク数と同じだとは思いもしなかったからです(笑)あらためてエンジニアとしてアルゴリズムを学ぶことの重要性を理解しました。
そして、C で書かれたプログラムを Swift に書き換えると以下のようになります。
func maxOverlapIntervalCount(starts: [CGFloat], ends: [CGFloat]) -> Int {
var maxOverlap = 0
var currentOverlap = 0
let starts = starts.sorted()
let ends = ends.sorted()
var i = 0
var j = 0
while i < starts.count, j < ends.count {
if starts[i] < ends[j] {
currentOverlap += 1
maxOverlap = max(maxOverlap, currentOverlap)
i += 1
} else {
currentOverlap -= 1
j += 1
}
}
return maxOverlap
}
これで描画に必要な列の最小値を求めることができました。ただ上記のアルゴリズムだと、どの予定同士が重なっていたかまで分からないので、処理と同時に最も重なりが大きい予定のグループを覚えておきます。さらにそのグループ以外にも重なっている予定のグループがあれば同時に覚えておきます。
重なっているグループの整列
上記のアルゴリズムの助けにより、描画に必要な列数と、最も重なりが大きいグループを見つけることができました。ここからすべきことは以下です。
- まず最も重なりが大きいグループの重なりを解く(列数と1つあたりの列の幅が決まる)
- それ以外の重なりが大きいグループから順番に重なりを解いていく
- 重なっていない予定はそのまま配置
- 予定同士の重なりがなくなるまで実行する
- 予定の重なりがなくなり次第、それぞれが確保する領域へ描画する(可能な限り横幅をとる)
| ① | ② | ③ |
|---|---|---|

|

|

|
上記で重なりを解くという表現をしていますが、予定が書かれたカードを順番に重ならない位置まで横にずらしていくイメージです。以上の手順により画像のような描画ができました。

最後に
予想外の苦労があった中でも、ユーザーさんからの要望に向き合えたという点で、バーチカルカレンダーの開発ができてとても良かったと感じています。また、Android と Web も同様の機能を提供しているのですが、実はそれぞれ違ったロジックで実現されてます(ある意味すごい)とは言え、ロジックは共通化した方がいいと思うので、そちらは今後の課題ということになりそうです。
TimeTreeの採用情報
TimeTreeのミッションに向かって一緒に挑戦してくれる仲間を探しています。TimeTreeで働くことに興味がある方はぜひ、Company Deck(会社紹介資料)や採用ページをご覧ください!
ここまでご覧いただきありがとうございました。
それでは良いお年をお迎えください🎅