§ はじめに
機械学習をはじめよう！と思ったときにまず最初の壁はPython 等のコーディング知識になるのではないでしょうか。機械学習で予測したいけどまずはPython 基本的な文法を覚えないと難しいし、そこまで時間がないし・・・という方もいらっしゃいますよね。
Alteryxにはデータ前準備（ETL）の機能だけじゃなく、機械学習の充実していてノンコーディングで機械学習の予測モデル作成、モデルの評価、予測値の取得ができ非常に気になっていたので今回試してみました。
また Tableau と連携して、データ理解、予測値を可視化することで、データから更なる価値を生み出すことができます。
早速体験していきましょう！
今回は、東京・中央線の中古マンションの価格を過去データから学習する予測モデルを作り、未知のデータに対して物件の条件からマンション価格を予測するステップをAlteryxとTableau を使って「ノンコーディング」で実装する方法をご紹介します。
予測モデルを作成するために利用する訓練データ（過去の取引データ）を国土交通省のサイトからダウンロードします。
対象となる市区町村、期間を選ぶと以下のような形式でデータを取得することができます。このままでは、機械学習の入力として利用するのが難しいため、諸々の地道なデータ前準備を行いますが、ここでは割愛します。
予測モデルの理解のしやすさのため、今回は、東京を東西に走る「中央線」の沿線にスコープを絞ることにします。
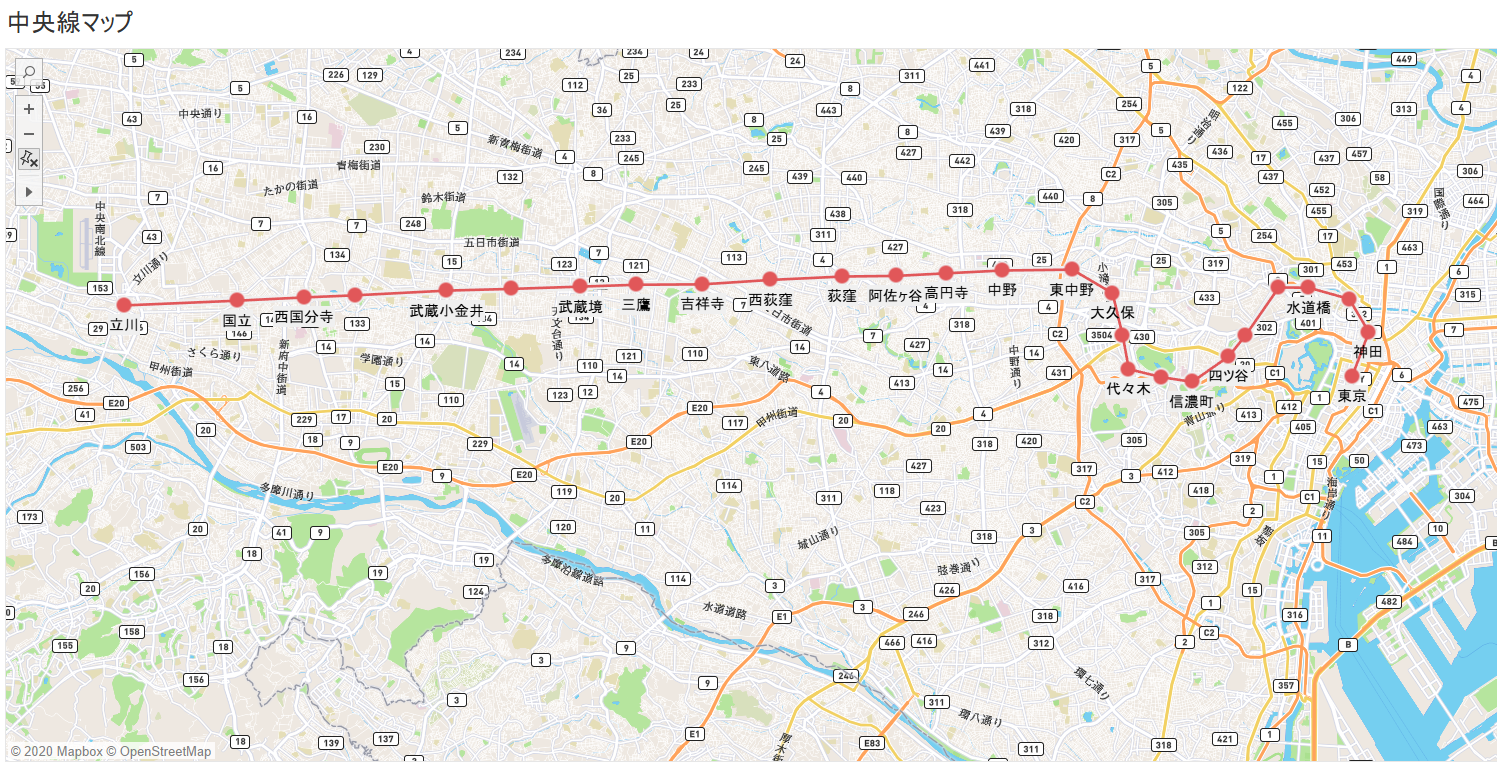
東京はに東西に長い形をしており、都心から離れるにつれて物件の相場は安くなることが分かっているので、新たな説明変数として「東京駅から最寄り駅までの直線距離」を追加することにします。
（実際の東西とは逆：最も東に位置する「東京駅」が左に、西に位置する「立川駅」は右に表示）
実際の駅の位置関係は以下のようになっています（Tableau の地図機能を利用して可視化）
データ前準備を経て、以下のように機械学習の入力データを作成します。（前準備処理のステップについては、書籍：Tableauで始めるデータサイエンス にて紹介しておりますのでご参考ください。）
それぞれの項目の説明は以下です。
| 項目名 | 説明 | データ型 |
| uid | 物件のユニークなID | 文字列型 |
| years | 築年数 | 整数型 |
| minutes | 最寄駅からの徒歩距離（分） | 整数型 |
| sqrm | 物件の㎡数 | 整数型 |
| distance | 東京駅と最寄り駅の直線距離（都心からどれだけ離れているか？） | 浮動小数点型 |
| renovate | 改装済みか否かフラグ | 整数型 ( 0 or 1 ) |
| express | 急行が止まるか否かのフラグ | 整数型 ( 0 or 1 ) |
| price | 取引価格（目的変数） | 整数型（単位：1円） |
§ 機械学習に伴うステップ
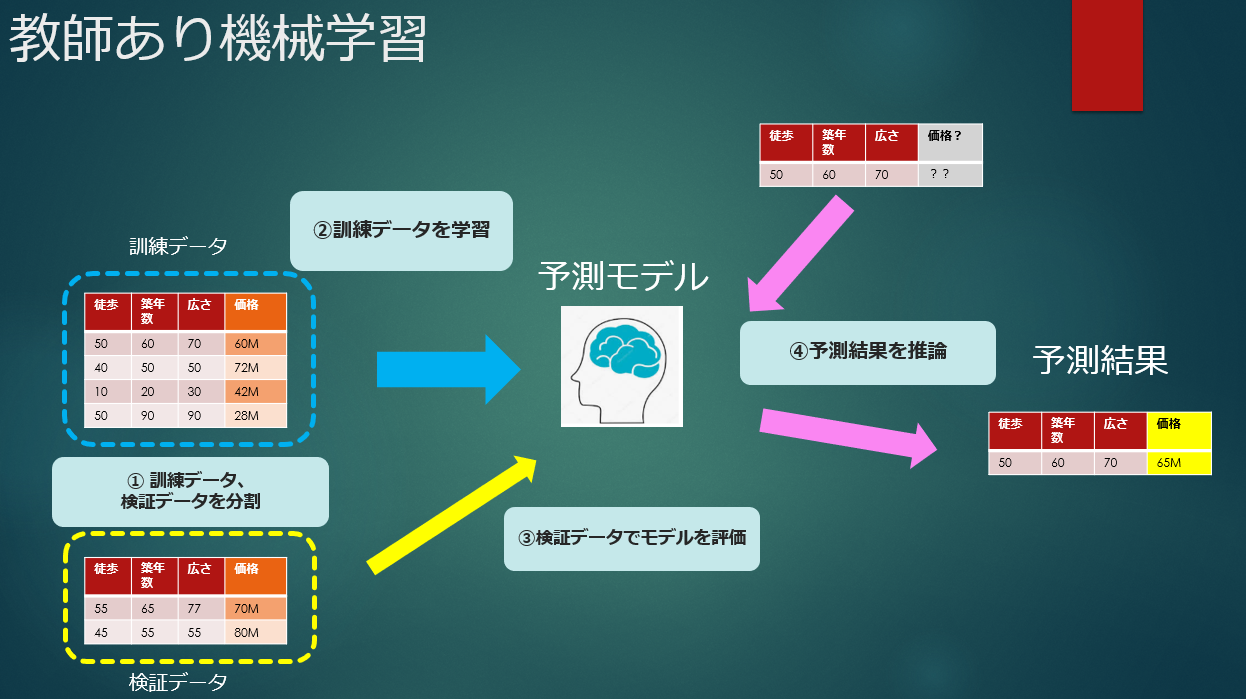
機械学習によって予測モデルを作るステップは以下のようになります。これらのステップAlteryxとTableau を使って、ノンコーディングで実装していきます。
① 訓練データと検証データを分割する
② 訓練データを使って予測モデル学習を行わせる
③ 検証データで予測モデルの精度を評価する
④ 結果の分からない未知のデータに対して予測値を得る
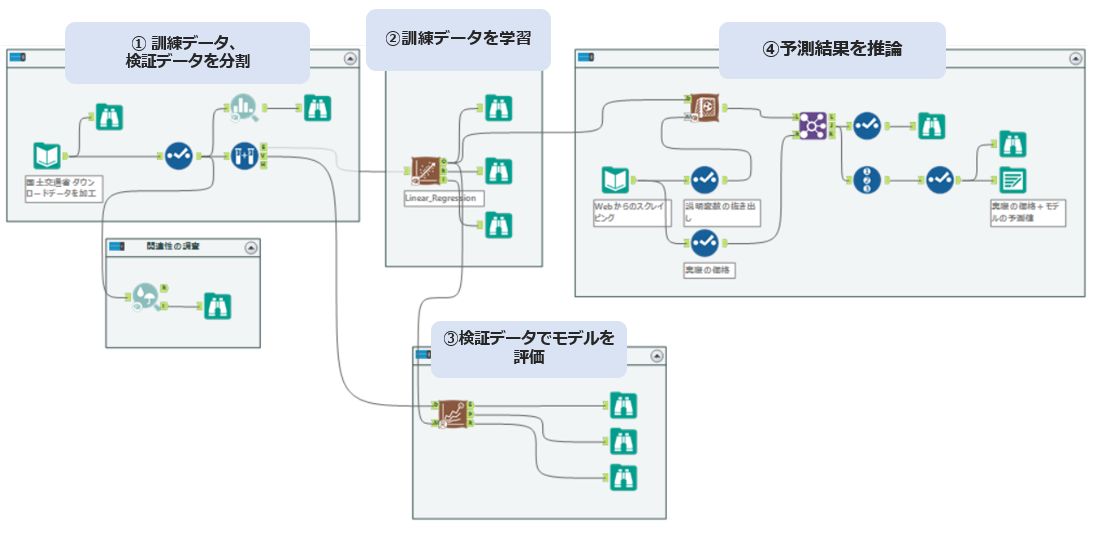
これを実現する最終的なAlteryxのフローは以下のようになります。
① 訓練データと検証データを分割する
それでは入力データを訓練データと検証データに分類するところまで実施してみましょう。
・ 国土交通省のサイトからダウンロードしたデータに接続します。
Input Data（データ入力）をドラッグして入力データに接続します。（※注１）
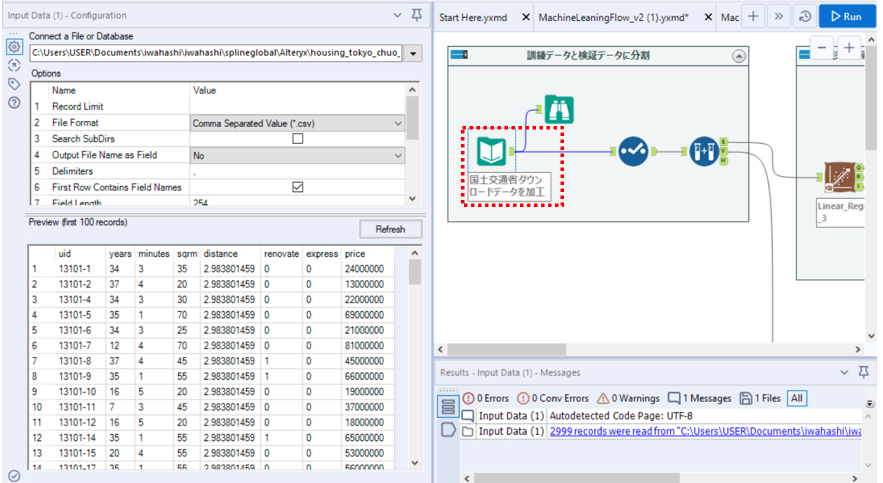
Select（セレクト）ノードで機械学習には利用しない”uid"を除外します。
"Price"でヒストグラムを書いておくと学習の妨げになるような外れ値（超高級マンション）がないことを確認できます。（現実の世界では、目を疑うほどの高額マンションは存在するのですが、ここでは事前に前処理で除外しています。）
少し脇道にそれますが、目的変数（予測したいフィールド）price がどの説明変数（予測の根拠となるフィールド）と、どの程度関連があるかを確認しておきましょう。AlteryxではAssociation Analitics （アソシエーション分析）を利用します。
目的変数 price に対して正の相関がある説明変数については赤色に、負の相関関係がある説明変数については青色で表示されます。price と years （築年数）は負の相関関係（-0.42)があり、price と sqrm（㎡数）には強い制の相関関係（0.75）があることが分かります。相関係数は-1 から+1の範囲を取ります。
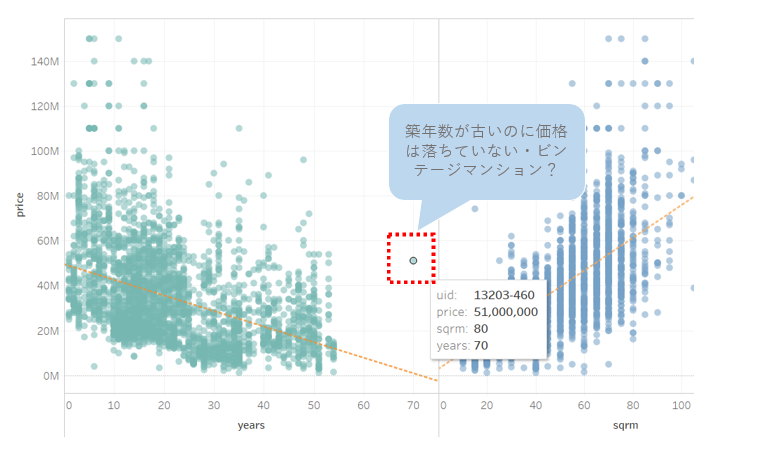
この時点で、Tableau を用いて散布図を書いて確認するということもできます。縦軸はprice、横軸（左）はyears（築年数）、横軸（右）はsqrm（㎡数）に取り散布図を書いたものです。Tableau で確認すると相関がより把握しやすいですし、外れ値のIDを確認することもできます。例えば、築年数は古いのに価格が落ちていない物件等もあり、これはもしかするとビンテージマンションなのかもしれません。
【Tableauで散布図表示】
【Tableauで散布図表示】
入力データを、予測モデルを作成するための訓練データと、訓練データよって学習した予測モデルを評価するための検証データに分割しうるために Create Sample （サンプル作成）を利用します。ここでは、訓練データ：検証データ＝７：３で分割します。このように訓練データと検証データをあらかじめ取り分けて置く手法は「ホールドアウト法」と呼ばれています。
② 訓練データを使って予測モデル学習を行わせる
線形モデル LinearRegression （線形回帰）に訓練データ Create Sample の訓練データ（E）を繋ぎます。目的変数（Target Vairiable）にpriceを設定し、説明変数（predictor variables）にprice 以外のすべての変数を選択します。
Linear Regression の出力には O（Output）、R（Report）、I（Interactive）があります。
O（Output：出力）はモデルそのもので次のステップで精度の確認や、実際の予測に利用します。
R（Report：レポート）は訓練済みモデルに関する情報です。Browse Tool （閲覧）を繋ぐと結果が確認できます。
Linear Modelは線形重回帰モデルなので、目的変数を説明変数の一次式で以下のように表すものとします。
| price = α1(years) + α2(minutes) + α3(sqrm)+ α4(distance) + α5(renovate )+ α5(express) + Intercept |
I（Interactive：インタラクティブ）はモデルの精度をダッシュボード形式で表示します。
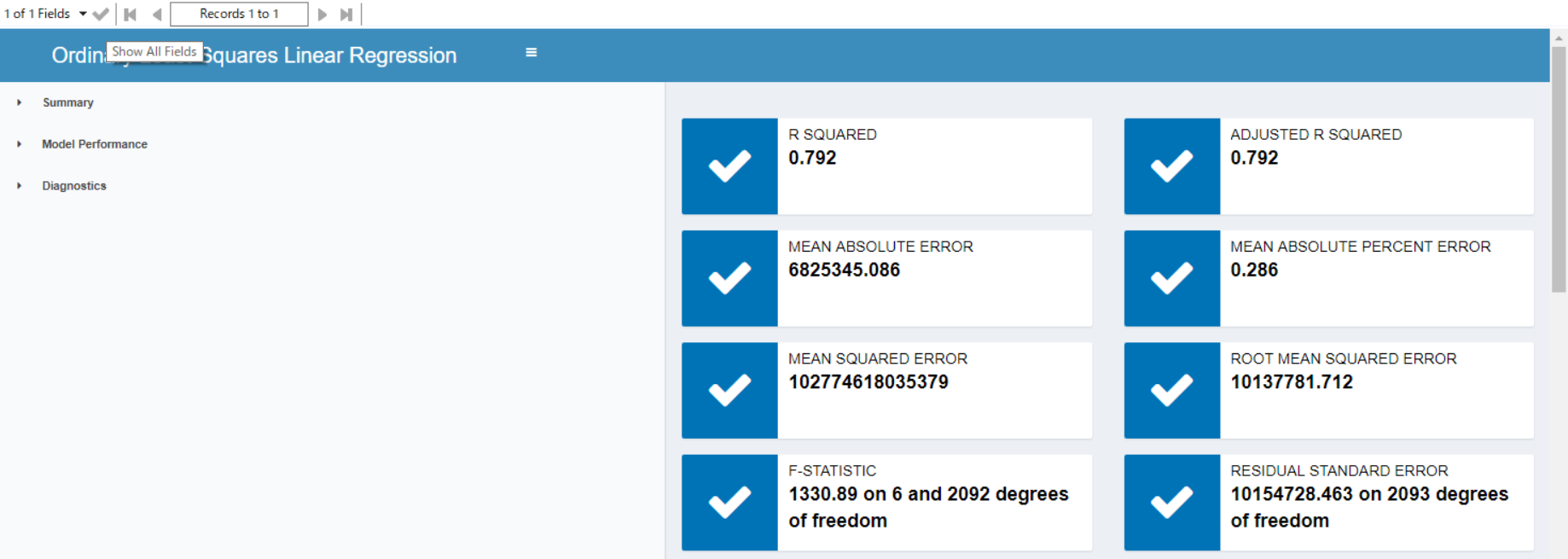
Summaryでは、R SQUARED（R２乗値）が１に近い値を示していることと、その他のERROR（誤差）指標が小さいことを確認します。
特にRMSE（Root Mean Square Error）は誤差の二乗を全て足し合わせ、標本数で割った平均の平方根を取ることで、標本当たりの誤差の大きさを示すモデルの精度の指標となります。この値が小さいということはモデルとして誤差が少ないことを示す一つの指標となります。
学習データに対してはRMSE＝10,137,781 となっているので、誤差の平均が1000万程度あると感覚的に解釈しても分かりやすいかもしれません。
Model Performance では横軸に実測、縦軸に予測値を出しています。予測＝実測 となりピタリと当てるモデルの場合はY=Xの直線の付近にプロットされるはずです。
Diagnosticsには残渣（Residual）と予測値（Fitted Value)の関係や Q-Qプロットが表示されます。こちらのダッシュボードでは、マウスをホバーしたポイントの具体的な数値が表示されます。
重回帰によって予測される値（非説明変数）の誤差の分布は平均０の正規分布に従っているという前提があり、誤差が正規分布に従っているかをNormal Q-Q プロットで確認することで、モデルの妥当性を検討することができます。非常に乱暴に理解するならば、Y=Xの直線に沿って分布しているほど当てあはまりの良いモデルと見れるでしょう。
Q-Qプロットの見方についてはこちらのhanaoriさんのNoteの記事が分かりやすかったためリンクを記載させていただきます。Normal Q-Q プロットを理解する
③ 検証データで予測モデルの精度を評価する
次に、取り分けておいた検証データを使って、訓練された予測モデルを評価してみましょう。
一般的には過学習を起こしていないかを確認するために、学習に利用していない、検証データ使ってモデルの精度を評価します。ここではAlteryxで Model Comparison というマクロ（※注２）を使うのが便利です。
関連する部分を見やすいように移動して拡大すると以下のようになります。Linear Regression の（O） と Model Comparison の（M）を繋ぎ、検証データ（V）とModel Comparison の（D）を繋ぎます。
それぞれの入力アンカーの意味は以下のようになります。
Reportとして以下のような内容が出力されます。
ここでは、RMSE（Root Mean Square Error) （※注３）に注目します。学習データに対してはRMSE＝10,137,781 となっていたに対し、検証データではRMSE=9,541,477 となったので、学習データに対して著しく誤差が大きくなる（過学習）は発生していないようです。誤差を小さくするためにできることはまだありそうですが、ここでは一度このモデルを実際の予測プロセスに利用することにしましょう。
④ 結果の分からない未知のデータに対して予測値を得る
モデルの評価が終わったら、実際にこのモデルを利用したマンション価格の「予測」を行います。本来は、築年数、駅からの徒歩（分）、㎡数・・・などの条件は分かるけれど、価格は分からない（目的変数が未知）場合に、そのマンションの価格を予測するというのが、本来「予測をする」ということなのですが、今回私たちは価格が未決定の物件情報を（不動産屋ではないので・・・）持ち合わせていません。
ですので、Web上に掲載されている中古マンションの情報からマンション価格をスクレイピングして、説明変数を抽出しモデルを適用して算出された予測値と、実際にWebに掲載されているマンション価格を突き合わせ、マンションの価格が適切なのかどうかを検証してみましょう。
Webからスクレイピングしたデータは以下のようになっています（説明変数として利用できるように前準備を完了しています。）
ここから説明変数を抜き出し、Score（スコアリング） に投入します。
Score の出力結果は以下のようになります。一番右端（predict）はモデルによって算出されたマンション価格の予測値となります。
ここで、この予測結果をスクレイピングしたデータともう一度連結すると、「Web上の掲示価格」と「予測モデルが算出した価格」を並べたデータを作ることができます。
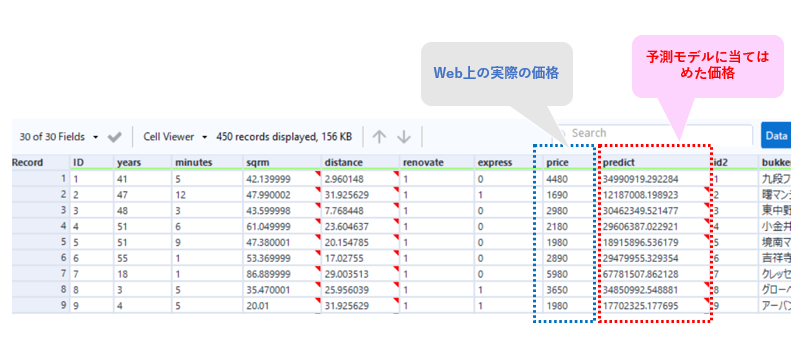
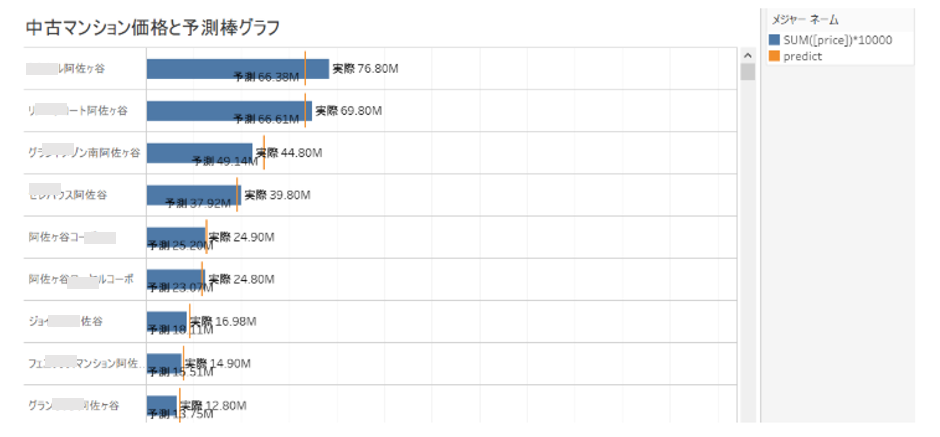
ここで「Web上の掲示価格」と「予測モデルが算出した予測価格」を物件ごとにTableau を使って可視化してみましょう。
これを駅ごとに箱ひげ図を書いて可視化すると以下のようになります。
四谷はレンジが広すぎて当てにならない、吉祥寺はお買い得が低い
、西国分寺はお買い得度が高い・・・といった発見があります。
これによって、東京駅から最寄り駅までの距離（いかに都心に近いか）という説明変数の他にも、「最寄り駅の人気度」などのあらたな要素を考慮しなければ説明が付かないといった示唆も得られるのかもしれません。（実際のお買い得かどうかは個人の価値観によるもので、一概に判断できないという前提で記事を執筆しております！）
また、さらなるデータ活用の発展形として、スクレイピングしたデータから緯度経度をジオコーディングし、お買い得物件を地図上にマッピングします。以下、オレンジ色は物件がお買い得、青色はお買い得ではないとことを意味し、丸の大きさは物件の価格です。地図上の物件のポイントをクリックすると、その物件の画像情報、Google Street Viewと連携して周辺の街の様子を確認することができます。もちろん（ここでは掲載していませんが）掲載Webページとリンクしてダッシュボード内に物件情報を表示することも可能となります。
§ おわりに
今回は機械学習の基本である、線形回帰モデルを使って中古マンションの価格を予測するモデルを作成しましたが、より精度の良いモデルを作成するために、物件の階数、街の人気度、方角等の上を説明変数として追加することも考えられます。また、他の予測モデルアルゴリズムとしてGBDT（Gradient Boost Dicision Tree）を利用し、ハイパーパラメータをチューニングするといった試行も必要になってくるかとおもいますので、こちらについては後続の記事にてご紹介できればと思います。どうぞご期待ください！
【補足】
注１： 最新バージョン2020.1からインストール時の言語選択ではなく、Alteryxを立ち上げたままで言語の変更ができるようになっています。→ 参考リンク
注２： Model Comparison のマクロはこちらからダウンロードできます。
注３： RMSEとは
【参考文献】
記事の執筆にあたり、アルテリックス・ジャパン合同会社 川村 洋平さん、酒井 信吾 さんの多大なる協力をいただきましたこと心より感謝いたします。