LoginSignup
5
2

More than 3 years have passed since last update.

上智大学エレラボAdvent Calendar 2020Day 7
@barisu(barisu)

グラフ生成アルゴリズム

Last updated at Posted at 2020-12-07

これは上智大学エレクトロニクスラボのAdvent Calendar7日目の記事です．

まえがき

交通網やwebページなどの様々なグラフが世の中にはありますが，そのような実データの中には共通する構造を持つものも多いです．例えば人間関係のネットワークは，ある程度小さな直径を持つことが知られています．一般にスモールワールド性と言われ，電力網なども同じ性質を持つそうです．このような世の中に存在するグラフの特性を守りつつ，好きなサイズのグラフを生成する方法をいくつか紹介します．

用語

  • 次数
    • あるノードが持つエッジの数のこと
  • 次数分布
    • 次数$k$を持つノードの割合を表した分布$p(k)$
  • クラスター係数
    • どの程度グラフが三角形を持つか表す指標$C$1 ．
  • スケールフリー・ネットワーク
    • 次数$k$を持つノード数$p(k)$は$p(k) \propto k^{-\gamma}$が成り立つグラフ（ネットワーク）
  • スモールワールド・ネットワーク
    • 直径が小さくクラスター係数が大きいグラフ（ネットワーク）

モデル

ランダムグラフ

アルゴリズム

かなり単純なアルゴリズムによって生成することができます．ただし下のアルゴリズムは参考文献1で紹介されているものです．定義とアルゴリズムは文献によって異なるようで，networkxでも複数のメソッドを提供しています2．

from random import random
import networkx as nx

# 実装した場合
def randomGraph(n,p):
    # 無向グラフを生成する
    graph = Graph()
    graph.add_nodes_from(range(n))
    # 確率pで任意のノード間をつなぐ
    for i in range(n):
        for j in range(i + 1,n):
            if random() < p:
                graph.add_edge(i,j)
    return graph

性質

全てのエッジを一様に選択しているため，次数分布は二項分布となります．実際にノード数を$1000$,$p=0.5$として次数分布をプロットしました．
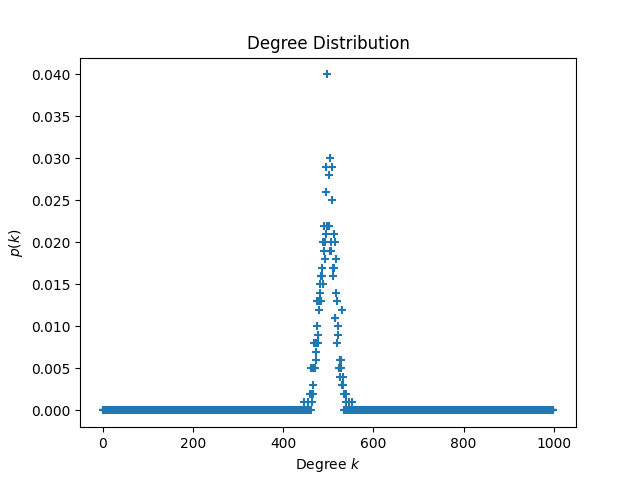
degree.png

紹介したアルゴリズムでは無向グラフとして生成していますが，文献によっては有向グラフとして生成される場合もあります．

WSモデル(Watts-Strogatz)

WatsとStrogatzによって発表されたものです．次数を大きくせずに，大きなクラスター係数と小さな直径からなるグラフを生成することができます．ここでも参考文献1で紹介されているアルゴリズムに従って実装しました．

アルゴリズム

import networkx as nx
from random import randint,random


def ws(n,k,p):
    # n ノード数
    # k 平均次数.ただし偶数に限る
    graph = nx.Graph()
    graph.add_nodes_from(range(n))

    if k%2 == 0:
        raise ValueError('kは偶数に限られます')
    if p < 0 or 1 < p:
        raise ValueError('pは割合です')
    for i in range(n):
        for j in range(k // 2):
            graph.add_edge(i,(i + j)%n)

    # ランダムに選択した辺から，片方の頂点を繋ぎ変える
    # 自己辺や多重辺を避け，u == w あるいは v == wを避ける処理を追加することもある
    for u,v in graph.edges:
        if random() > p:
            continue
        graph.remove_edge(u,v)
        w = randint(0,n - 1)
        if random() < 0.5:
            graph.add_edge(u,w)
        else:
            graph.add_edge(v,w)    
    return graph

今回は簡潔に最小限の要件だけ満たした実装としました．networkxでは同様のWSモデル3や連結なWSモデル4のグラフを生成するためのメソッドを提供しています．

性質

直径とクラスター係数の大きさは $p$ によって決定され，スモールワールド・ネットワークの要件を満たします．ただしスケールフリー・ネットワークの要件は満たしません．また直径とクラスター係数は $p$ が大きくなるにつれて小さくなります．厳密な関係については以下で述べます．

クラスター係数

確率 $p$ で既にあるエッジを張り替える以前の状態（拡張サイクル）のクラスター係数を考えると，$\frac{3(k/2) - 3}{4(k/2) - 2}$ となります．1つの三角形を構成する3つのエッジが張り替えられずに残る確率は $(1-p)^3$ ですから，1つのクラスターに対して，エッジを張り替えた際に残るクラスターの数の期待値は $(1-p)^3$ となります．したがって，単純にクラスター係数 $C = \frac{3k-6}{4k-4}(1-p)^3$ と表すことができます．これはエッジを張り替えたのちにできるクラスターを無視したもので当然厳密ではありませんが，実測値と経験的に一致することが知られているようです．

直径

参考文献１で求め方が紹介されていますが，やや複雑であるためここでは言及を避けます．

BAモデル(Barabási-Albert)

アルゴリズム

優先的選択に基づいて，既にあるグラフに1つずつノードを追加し，既存のノード $m$ 個に対してエッジを繋げることでグラフを生成します．初期値であるグラフは連結であること以外の条件を課されません．ノード $i$ の次数を $k_i$ と表記し，既に存在するノード数を $N'$ とすると，新しいノードを追加した際にノード $i$ にエッジを繋げる確率は $\frac{k_i}{\sum^{N'}_{j = 1} k_j }$ となります．

import networkx as nx
from random import sample

def ba(n,m):
    # 初期値とするグラフは連結であればよい
    # 今回は初期値を頂点数mの完全グラフとする
    graph = nx.complete_graph(m)

    # 確率を管理する用のリスト
    source = [i for i in range(m) for _ in range(m - 1)]

    for i in range( len(graph) , n + len(graph) ):
        # 新たなノードiを追加する
        graph.add_node(i)

        # 前述の確率に従って繋げるノードを選択する
        targets = sample(source,m)
        for target in targets:
            graph.add_edge(i,target)

            # 確率の管理
            source.append(target)
            source.append(i)

    return graph

同一のアルゴリズムがnetworkxのメソッドとして実装されています．5

性質

スケールフリー・ネットワークの要件を満たし，直径の点ではスモールワールド・ネットワークの要件を満たします．また $p(k) \propto k^{-3} $ であることが知られています．
実際に次数分布がべき乗則を満たしているか確認します．その際なだらかにプロットするために，縦軸には次数分布の累積をとることにします．
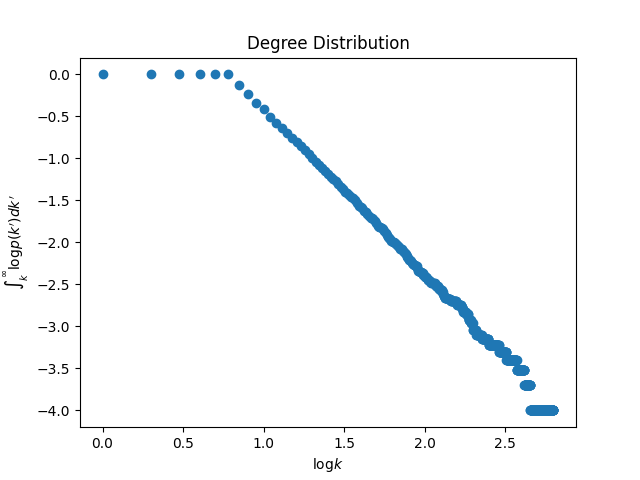
qiitaBA.png

両対数のプロットで直線になっているので，べき乗則に従っていることが分かります．また任意のノードにおいて，少なくとも $m$ 個のエッジを持つように設定しているので次数 $0$ に近い部分では縦軸の値が $0$ に留まっています．

有向スケールフリー・ネットワーク

ここまで主に無向グラフを生成していましたが，最後に有向なスケールフリー・ネットワークを生成する方法を紹介します．これはnetworkxにdirected.scale_free_graphとして実装されているアルゴリズムです．

アルゴリズム

基本的にはBAと同じように既存のグラフにノードを順次追加していく形を取ります．ただし無向グラフではないので，接続するエッジの向きに留意しなければなりません．
以下のいずれかを繰り返すことでノード数が $n$ になった時点で終了です．

  1. 確率 $\alpha$ で実行．新しいノード -> 既存のノード
  2. 確率 $\beta$ で実行．既存のノード -> 既存のノード
  3. 確率 $\gamma$ で実行．既存のノード -> 新しいノード

この時の既存のノードの選び方を説明するために，いくつか記法を整理します．

  • $N_t$
    • ステップ $t$ におけるグラフのノード数
  • $E_t$
    • ステップ $t$ におけるグラフのエッジ数
  • $\delta_{in}$
    • 既に入次数の高いノードの優先度を決定するバイアス
  • $\delta_{out}$
    • 既に出次数の高いノードの優先度を決定するバイアス

ノード $i$ が選ばれる確率は $ \frac{k_i + \delta_{in,out}}{E_t + \delta_{in,out} \cdot N_t} $ となります．

性質

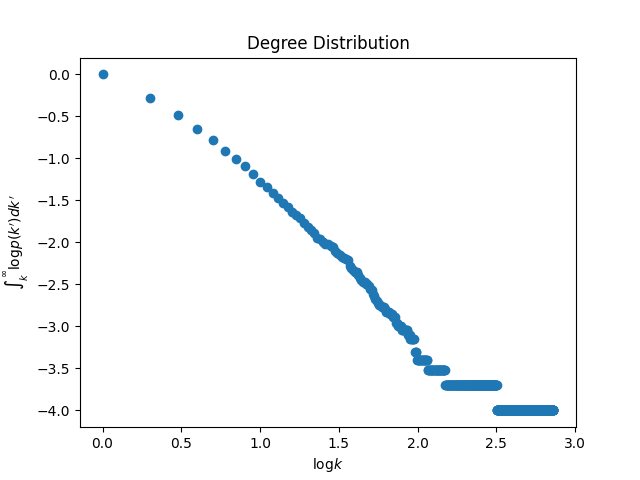
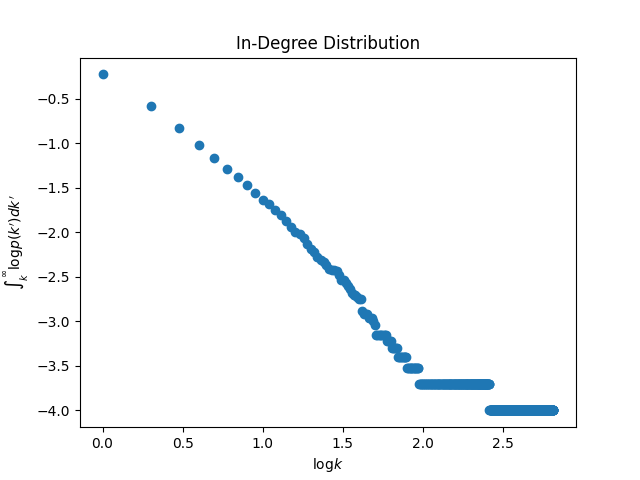
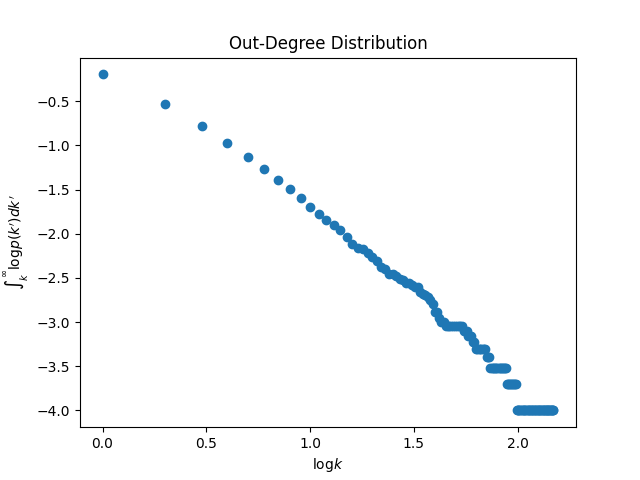
入次数と出次数の両方でべき乗則に従います．また自己辺や多重辺を容認するアルゴリズムになっていますが，$n$ が十分大きければ最終的に削除しても次数分布に大きな影響はありません．$n = 10^4,
\alpha=0.3,\beta=0.4,\gamma=0.3$ として自己辺と多重辺を削除したグラフの次数分布を下にプロットします．
次数分布
degree.png
入次数分布
InLog.png
出次数分布
OutLog.png

参考文献

  1. 増田直紀 and 今野紀雄, 2010. 複雑ネットワーク: 基礎から応用まで. 近代科学社
  2. B. Bollobás, C. Borgs, J. Chayes, and O. Riordan, Directed scale-free graphs, Proceedings of the fourteenth annual ACM-SIAM Symposium on Discrete Algorithms, 132–139, 2003.

  1. こちらの定義を参考にしてください．http://syrinx.q.t.u-tokyo.ac.jp/tori/lecture/complex/network2.pdf ↩

  2. https://networkx.org/documentation/stable/reference/generators.html#module-networkx.generators.random_graphs ↩

  3. https://networkx.org/documentation/stable/reference/generated/networkx.generators.random_graphs.watts_strogatz_graph.html#networkx.generators.random_graphs.watts_strogatz_graph ↩

  4. https://networkx.org/documentation/stable/reference/generated/networkx.generators.random_graphs.connected_watts_strogatz_graph.html#networkx.generators.random_graphs.connected_watts_strogatz_graph ↩

  5. https://networkx.org/documentation/stable/reference/generated/networkx.generators.random_graphs.barabasi_albert_graph.html#networkx.generators.random_graphs.barabasi_albert_graph ↩

5
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
5
2