はじめに
1-5の記事で仮説検定について紹介させていただきました。
ただ仮説検定にはほかにも様々な目的に適したものがあるので、そちらの検定を紹介したいと思います。
目次
- データタイプ
- 量的変数の性質
- 一標本のt検定
- 二標本のt検定
- 正規性の検定
- 等分散性の検定
- ノンパラメトリック検定
- 分散分析
- 多重比較
1. データタイプ
1-5の記事では2群間の比較の検定について説明しました。ただ仮説検定には、解析の目的やデータの性質によってさまざまな検定が存在するので本記事では一部を紹介したいと思います。
前提としてどの検定でも以下の流れは基本的に同じだと思っていてください。
- 帰無仮説、対立仮説を設定
- データから検定統計量を計算
- 帰無仮説が正しい仮定の下で統計量の分布を考え、その中でデータから得られた統計量がどこに位置するかをもとめることでp値を計算
まずデータのタイプによって解析手法が異なるので、まずデータタイプについて確認するようにしましょう
- 量的変数と量的変数間の関係
- カテゴリ変数とカテゴリ変数間の関係
- 量的変数とカテゴリ変数間の関係
1の量的変数間の関係については、散布図を用いてプロットを描くことができます。また回帰分析を用いて分析することもできますが、こちらについては1-7の記事で紹介したいと思います。
2のカテゴリ変数間の関係については、分割表を使うことが多いです。
3の量的変数とカテゴリ変数については、1-5の記事でやった血圧の例などがあります。つまり2群間の比較のt検定は、量的変数とカテゴリ変数という2つの変数間の関係を調べていると判明しました。
2. 量的変数の性質
パラメトリック検定
t検定はデータを発生させている母集団が正規分布であることを仮定した手法でした。このように母集団が数学的に扱える、特定の分布に従っていると仮定を置いた時の仮説検定のこと。ほとんどが母集団の分布が正規分布の場合です。
実際にデータが正規性を満たしているかについては、後ほど説明する正規性の検定を使うとよいでしょう。
ノンパラメトリック検定
母集団分布が特定の分布を仮定できない場合、例えば左右非対称な分布や外れ値がある分布では、平均や標準偏差といったパラメータはあまり役に立ちません。このような仮説検定のこと。
1-5の記事では、あまり気にしませんでしたが二標本のt-検定(2群間の比較のt検定)はパラメトリック検定なので、処理群と対照群の各データが正規性を満たしていないと使うことができない検定となっております。
3. 一標本のt検定
1-5で実施した二標本のt検定の一標本版です。
この検定の目的、仮説は次のようになります。
目的:標本がどのような平均値をもつ母集団から得られたかを調査
帰無仮説:母集団平均は$\mu = 〇〇$である。
対立仮説:母集団平均は$\mu = 〇〇$ではない。
帰無仮説が正しいと仮定して統計量を計算していく。
標本誤差の分布
標本誤差$\bar x - \mu$は、平均$0$・標準偏差$s/\sqrt n$の正規分布に従う。
ここは二標本のt検定と似ているので、例題などは省略する。
4. 二標本のt検定
1-5で説明した2群間の比較のt検定のことです。
こちらは2つの群での平均値を比較しています。
帰無仮説:2つの群の平均値は等しい(平均値の差が0)
対立仮説:2つの群の平均値は等しくない(平均値の差が0ではない)
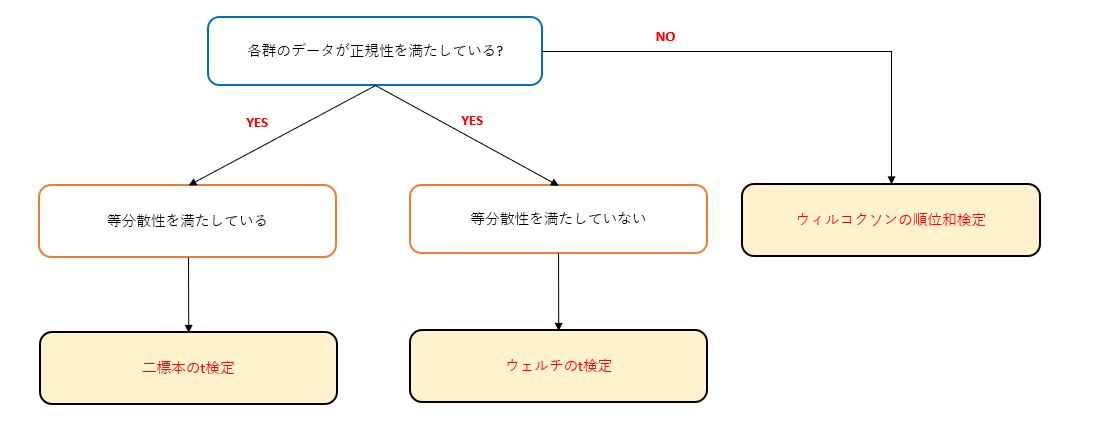
こちらの検定では以下グラフの条件を満たしていないと使用することはできないです。
各群のデータがそれぞれ正規性を満たしていないといけません。どちらか一方でも満たしていなければ、ノンパラメトリックになるのでパラメトリック検定である二標本のt検定は実施できません。また正規性を満たしいても、2群間の母集団分散が等しくなければ二標本のt検定は使用できません。この場合代わりにウェルチのt検定を用います。
1-5の記事で扱ってきた二標本のt検定は、対応のない検定と呼ばれるものでした。「対応のない」とは2つの群の被験者には対応関係がないということ。各群で10人ずつ標本を抽出したら、合計20人ほど被験者が必要になります。
対応ありの検定は、新薬の例でいうと各被験者から薬を飲む前と飲んだ後に血圧を測定して効果を調べます。
つまり2群間の被験者は対応があるといえます。この場合例えば、新薬を飲む前の血圧が150で飲んだ後の血圧が110だとしたらその差を-40として記録できます。この差に注目して検定を実施すれば、一標本のt検定で検定を実施することができます。
5. 正規性の検定
パラメトリック検定では、各群のデータに正規性が必要です。
正規性を調べる手法は、視覚的な判断ではQ-Qプロットを使い、仮説検定ではシャピロ・ウィルク検定やコルモゴロフ・スミノフ検定を使います。
基本的にサンプルサイズが小さいときはシャピロ・ウィルク検定を使い、大きいときはコルモゴロフ・スミノフ検定を使うとよいでしょう。
正規性の検定の仮説は次のように設定します。
帰無仮説:母集団が正規分布である
対立仮説:母集団が正規分布ではない
例えば帰無仮説が棄却できないから、データが正規分布に従うと積極的に言うことはできません。(判断保留になるため)
ニュアンスでいうと正規分布の可能性もあるし、それ以外の分布の可能性もある程度だと思ってください。
では実際に1-5で使用した下記データに対して正規性の検定を実施してみたいと思います。
計算などはRで行うため、途中式などは省略します。
| 新薬(母集団A) | 偽薬(母集団B) |
|---|---|
| 142 | 145 |
| 132 | 130 |
| 127 | 150 |
| 140 | 142 |
| 142 | 145 |
| 130 | 155 |
| 126 | 148 |
母集団A
p値を見ると0.1349なので有意水準5%で考えるならば、$p > \alpha$となり帰無仮説を棄却することはできない。
よって母集団Aは正規性を満たしている可能性がある

母集団B
p値を見ると0.4892なので、$p > \alpha$となり帰無仮説を棄却することはできない。
よって母集団Bは正規性を満たしている可能性がある

6. 等分散性の検定
t検定を行うには正規性のほかに、等分散性も考慮する必要があります。
つまり比較対象が分散が等しい母集団から得られたかどうかを調査します。
等分散性を調べる検定は、バートレット検定やルビーン検定があります。
この場合、次の前提で仮説検定を実行します。
帰無仮説:2つの母集団の分散が等しい
対立仮説:2つの母集団の分散が等しくない
2つの検定の違いは、次のような基準になります。
バートレット検定:母集団が正規分布に従っているとき
ルビーン検定:母集団の正規性が保証できないとき
また2群間以上であれば、いくつもの群間でこの2つの検定は使用できます。
では先ほどの正規性の例題と同様にこちらも検証してみたいと思います。
今回は正規性の検定の結果も踏まえて、バートレット検定を使用したいと思います。
(使用するデータは正規性に用いたデータと同じものを使用します。)
Rで検定をするとp値が0.8006となりました。これは有意水準5%で考えたとき、$p > \alpha$となるので帰無仮説を棄却することはできません。
よって「2つの母集団の分散が等しい」仮説を棄却することはできず、2つの母集団は等分散性を満たしている可能性があると結論付けられる。

ただここで1点注意があり、複数の検定を行うことはあまりお勧めされていません。今回の例でいえば、正規性の検定→等分散性の検定→二標本のt検定と3つの検定を実施しました。今回はあくまで例として紹介しましたが、実際の検定を実施する場合は多重性の観点からも避けたほうが良いといえます。こちらについては後ほどまた説明いたします。
7. ノンパラメトリック版の2標本検定
各群に正規性がない場合は、先ほどのグラフでも説明しましたがノンパラメトリック検定に分類される検定を実施する必要があります。この場合平均値ではなく、分布の位置を示す他の代表値に着目して分析を行います。
最も有名なノンパラメトリック検定の代表的な検定は、ウィルコクソンの順位和検定です。
これは平均値の代わりにデータの各値からランクに基づいた検定を実施します。ここでいうランクとは、大きさ順に並べたときに何番目に位置するかを表す値となっております。
ウィルコクソンの順位和検定の前提は次のようになります。
帰無仮説:2つの母集団の位置が同じである
対立仮説:2つの母集団の位置が異なる
母集団の位置が同じというのは、2つの母集団が一致するということ。つまり平均や分散などの代表値が同じことを示す。
ウィルコクソン順位和検定はノンパラメトリック検定であるが、母集団が正規性を満たしていたとしても使用することができる。ただその場合検出力が小さくなり第2種の過誤を起こす確率が高くなってしまいます。母集団の正規性が未知な場合やあいまいな場合のみ使うとよいでしょう。
ウィルコクソン順位和検定は対応なしの検定となります。対応ありの検定はウィルコクソンの符号順位検定となります。今回対応ありの検定については説明を省かせていただきます。
続いてウィルコクソンの順位和検定の簡単な考え方を説明します。
母集団A,Bから次のようなデータが得られたとする。この時小さい順にランク付けを行う。()の中身が順位。
順位を付けたらそれぞれの母集団で順位和を求める。母集団Aの順位和=$1+4+3=8$、母集団Bの順位和=$5+2+6=13$この順位和を用いて統計量を計算し検定を行う。
| 母集団A | 母集団B |
|---|---|
| 142(4) | 145(5) |
| 132(3) | 130(2) |
| 127(1) | 150(6) |
ノンパラメトリック検定は他にもフリグナー・ポリセロ検定やブルネル・ムンツェル検定などがありますが、ここでの説明は省きます。
8. 分散分析
ここでは3群以上の平均値の比較をする、分散分析(ANOVA)について説明します。分散分析といいながらこちらの手法は平均値の比較を行う検定となっています。また分散分析はパラメトリック検定なので、各群は正規性を満たしていないといけません。1つでも正規性を満たしていない場合はノンパラメトリック検定を使う必要があります。
続いて分散分析の前提条件は次のようになります。
帰無仮説:全ての群の平均が等しい
対立仮説:少なくとも1つのペアに差がある
分散分析を説明するにあたって、以下の例題を参考に説明していきたいと思います。
例:肥料A,B,Cをそれぞれ与えて植物を育てたときの、茎の長さを比較します。
帰無仮説:全ての群の平均値が等しい(肥料の効果に差はない)
対立仮説:少なくとも1つのペアに差がある(少なくとも1つの肥料間に差がある)
まず各群と全体の平均を求める。
$\bar x_A = 32.5、\bar x_B = 34.2, \bar x_C = 38.9, \bar x = 35.2$
各データ$x_i$と全体平均の差を考える。(今回はAに対して考えるが、B・Cも同じ考え)
$x_i - \bar x = (x_i - \bar x_A) + (\bar x_A - \bar x)$
つまり各データと全体平均の差は、群内のばらつき$x_i - \bar x_A$(群内変動)と群間のばらつき$\bar x_A - \bar x$(群間変動)の2つに分解できる。
続いて分散分析表を作成する。分散分析表を作成できれば、検定統計量の計算が簡単にできるので覚えましょう。
- まず群間変動と群内変動の自由度を求めます。
- 群は全部で3つなので、I=3となります。よって群間変動の自由度は、$I-1=2$となります。
- 群間変動の自由度は$N-I$となります。$N$はサンプルサイズなので、$N-I=18-3=15$となります。
- 平方和を求めます。
- $BSS = \Sigma_{i=1}^I n(\bar x_{i・} - \bar x_{・・})^2\ $で求められます。今回だと、$6(32.5-35.2)^2 + 6(34.2-35.2)^2 + 6(38.9-35.2)^2=131.88\ $
- $WSS = \Sigma_{i=1}^I \Sigma_{j=1}^n (x_{ij} - \bar x_{i・})^2\ $ で求められる。今回だと、$(32.5-32.5)^2+(34.2-32.5)^2+・・・+(39.5-38.9)^2=16.235\ $
- 平均平方を求めます
- 群間変動:$\frac{131.88}{2}=65.94\ $
- 群内変動:$\frac{16.235}{15}=1.082\ $
- F統計量を求める
- $F=\frac{BSS/(I-1)}{WSS/(N-I)}=60.94\ $
F分布表を見ると、$F(2,15)$の5%点の値は、3.68ということがわかる。つまり今回3.59よりもF統計量の値ははるかに大きいので、帰無仮説を棄却し対立仮説を採択する。

今回分散分析の計算過程も知ってほしかったので数学ベースで説明したが、実際にデータ分析をする際はRを使えば一瞬で解析できる。
実際にRで解析した結果が次に当たる。この結果p値=6.468e-08とめちゃくちゃ小さい値をとっている。つまり$p<\alpha$となり帰無仮説を棄却することが一瞬でわかると思います。
分散分析のお話はここで終了ですが、最後に自由度について説明したいと思います。
自由度とは自由に動ける変数の数を表します。
例えば、$x_1+x_2+x_3=10$としたとき、$x_1=4,x_2=5$を与えたとすると$x_3$は自動的に1になることがわかります。つまりこの場合でいうと自由度は2となります。($x_1,x_2$)
9. 多重比較
先ほどの分散分析の結果帰無仮説を棄却しましたので、少なくとも1つのペアに対して肥料の効果があることがわかりました。ただ分散分析ではどのペアにおいて肥料の効果があるかまではわかりません。そのためどのペアで差があったのかを調べるには、多重比較をする必要があります。
例えば先の例でいえば、各ペアの差を調べるには、二標本のt検定を3回実施する必要があると思います。ただ検定を何度も実施すると第一種の過誤の確率が増加してしまうことわかっております。
t検定を3回繰り返すと、少なくとも1つのペアで第一種の過誤を起こす確率は、$1 - (どのペアでも第一種の過誤を起こさない確率)^3 = 1-(0.95)^3 = 0.143$となります。つまり分散分析で全体として設定していた$\alpha=0.05$を上回ってしまします。
これだと群の数が増えるほど第一種の過誤確率は起きやすくなってしまいます。
こちらの対応策については別の記事で紹介しますが、この多重性を回避する1つの方法で多重比較があります。
これは基本的なアイディアで検定を繰り返すごとに有意水準の値を厳しい値に変更するといったものです。全ての検定を通して有意水準5%を保つようにします。
最も単純な多重比較手法として、ボンフェロー二法があります。
これは有意水準$\alpha$と検定回数$k$を用いて、1回1回の検定では$\alpha/k$を基準に仮説検定を実施します。
ただこの検定は検出力が低い傾向があるため、本当は差があるときに差があると主張しにくくなる欠点がります。
通常分散分析を行った後はボンフェローニ法よりも検出力が改善されたテューキーの検定を使うことが多いです。
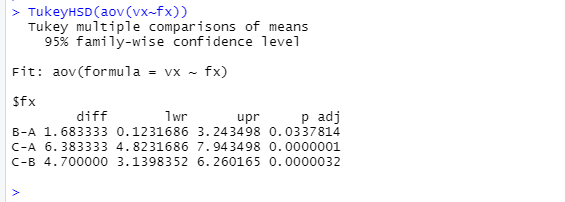
実際に先ほどの肥料の例に対してテューキーの検定を実施してみた。
この結果の見方は次のようになる
- diff:平均値の差。B-Aでいうと、BのほうがAよりも平均値が1.683333大きいことを表している。
- lwr upr:信頼区間の下限値と上限値を示している
- p adj:p値
今回でいうと各群間のp値は有意水準$\alpha$より小さいことがわかるので、各群間で肥料に差があるといえる。
他にも対照群との比較にだけ興味がある場合はダネット検定を用いるとよい。全ての群間を比較するテューキーの検定よりも検出力が向上します。また群間の順位が想定できる場合は。ウィリアムズ検定を使うほうがより検出力が上がります。
今まで紹介した多重比較手法は、単独で使用することも可能なので、必ず分散分析を行った後に実施しないといけないわけではありません。
最後にノンパラメトリック検定版の分散分析や多重比較についてこの記事は終わりにします。
少なくとも1つの群において正規性がない場合は、分散分析の代わりにクラスカル・ウォリス検定を使うことが推奨されています。
またテューキーの検定に相当するのがスチール・ドワス検定で、ダネット検定に相当するのがスチール検定です