はじめに

1-8章で説明した量的変数同士の関係についてより広い枠組みで説明を行います。
例えば説明変数を増やしたり、目的変数の種類を変更、回帰モデルの形を変更などなどです。

1. 重回帰

1-8の記事で紹介した線形単回帰モデルでは説明変数の数は１つでしたが、複数の説明変数を同時に導入することもでき、重回帰と呼びます。一般的に$k$個の説明変数を持つ線形重回帰モデルは次のように書くことができます。

y = a + b_1x_1 + b_2x_2 + ・・・ +b_kx_k +\epsilon

$a,b_1,b_2,・・・,b_k$として$k+1$個のパラメータを持ちます。
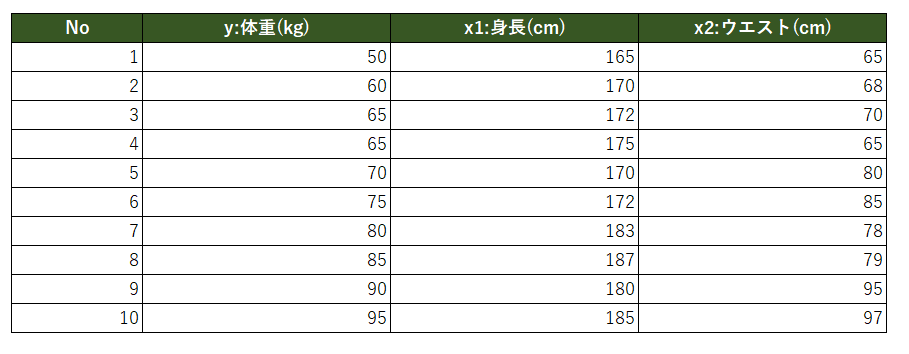
では例題について考えてみましょう。今回は体重・身長・ウエストの3つの変数があり、体重を目的変数、身長とウエストを説明変数としたいと思います。直感的に身長が高いと体重は重そうですし、ウエストが太いと体重は重そうだとわかるので、この２つの説明変数を使用することで体重をよく説明するモデル$y=a+b_1x_1+b_2x_2+\epsilon$を作っていきたいと思います。$a$は切片、$b_1$は$x_2$を固定しながら$x_1$を１増加させたときの$y$の増加量、$b_2$はその逆を表しています。これら傾き$b_1,b_2$を重回帰では偏回帰係数といいます。（それぞれのパラメータの推測は単回帰分析と同じく最小二乗法を用いるのでここでの説明は省きます。）
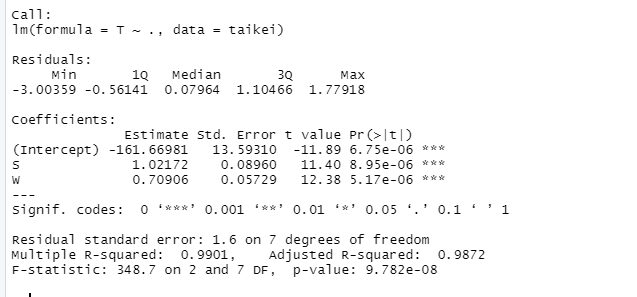
では実際に以下データに対してRで重回帰分析を実施しましたので、その結果を見てみましょう。

上記結果より回帰式は

y=-161.67 + 1.02x_1 + 0.71x_2

と得られました。また各パラメータのp値、全体のp値(一番下の行)も有意水準1%でも帰無仮説を棄却でき、調整済み決定係数の値も0.98なのでこの回帰モデルの説明力が高いと判断できる。(帰無仮説は偏回帰係数が全て０のモデルと考えます）

2. 標準化偏回帰係数

偏回帰係数は説明変数のばらつきの大きさや単位によって大きく変化するため、偏回帰係数同士の比較をすることはできません。上記体重・身長・ウエストの例でいうところの、$1.02$のほうが$0.71$よりも大きい数値なので目的変数に与える影響が身長のほうが大きいみたいな解釈はしてはいけません。もし偏回帰係数同士の比較を行いたい場合は標準化を実施するようにしましょう。標準化した場合の偏回帰係数を標準化偏回帰係数といいます。

標準化偏回帰係数は、回帰分析を実施する前にそれぞれの説明変数を平均0標準偏差1に変換し、そこから回帰分析をして求めた回帰係数のことです。つまり偏回帰係数を標準化するというよりか、データを標準化するイメージのほうが良いかもしれないです。標準化の方法は正規分布らへんの記事で紹介したものと同じで、次のようになります。

X_i = \frac{x_i - x_iの平均}{x_iの標準偏差}\\

ただデータの標準化もRを用いれば簡単にできますので、あまり気にしなくても大丈夫です。
では実際に重回帰の際に使用したデータを標準化して再度回帰分析を実施してみたいと思います。
今回使用したコードは以下になります。(今後なるべく使用したコードも貼り付けていきます。)ちなみに重回帰の章で実施した方法は、以下の標準化を飛ばせば同じような結果が出せます。

#データ用意
weight <- c(50,60,65,65,70,75,80,85,90,95)
height <- c(165,170,172,175,170,172,183,187,180,185)
waist <- c(65,68,70,65,80,85,78,79,95,97)

# データフレーム化
taikei <- data.frame(weight,height,waist)

#データの標準化
stan_taikei <- scale(taikei)
df_stan_taikei <- data.frame(stan_taikei)

#重回帰
taikei.lm <- lm(weight~.,data=df_stan_taikei)
summary(tailei.lm)

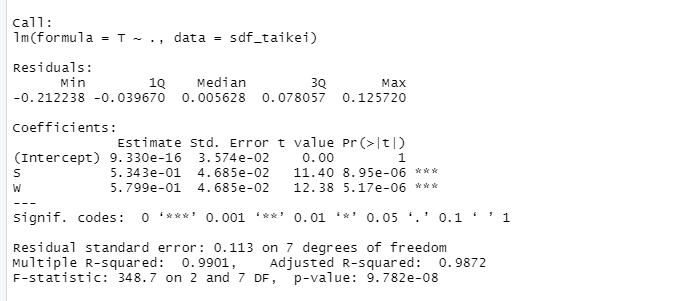
分析結果は次のようになります。
使用しているデータは同じなので決定係数や統計的有意性に変化は特にありませんね。

得られた回帰係数より回帰式は次にようになります。

y = 9.330e^{-16} + 0.5343x_1 + 0.5799x_2\\

標準化偏回帰係数を比較するとほとんど同じ値だが、強いて言えばウェストのほうが体重に与える影響は大きいということがわかりました。以上で標準化偏回帰係数の説明は終わりです。最後に偏回帰係数の相関についてお話しします。

偏回帰係数(標準化偏回帰係数)は、$x_i$以外の説明変数を固定したまま$x_i$が１増えたときの$y$の増加量を表しています。ただ説明変数同士に相関がある場合、$x_i$以外の説明変数を固定したまま$x_i$を独立に動かすことはできず、相関関係のある変数も同時に動いてしまいます。相関係数が１に近いような強く相関する場合においては、多重共線性があることを疑い、対処する必要しなければいけません。こちらについては後ほど説明しますが、一旦ざっくりと抑えといてください。

3. ダミー変数

回帰分析では量的変数だけではなくカテゴリ変数を用いることもできます。カテゴリ変数を回帰分析に用いる場合は、0 or 1のダミー変数として説明変数の導入します。例えば運動が嫌い/好きというカテゴリを説明変数に組み込む場合、運動が嫌い=0・運動が好き=1とします(0,1は逆でも構いません)。

ではカテゴリ数が３つ以上の場合はどのように対応をするべきでしょうか。例えば血液型A,B,O,ABについて考えてみると、２つのカテゴリの場合と異なり、４つのカテゴリを$x=0,1,2,3$と数値対応させることはできません。あくまでダミー変数として使ってよいのは、$0,1$のみです。

３つ以上の場合、0 or 1のダミー変数を(カテゴリの数-1)個用意します。血液型の例ではカテゴリ数が４つなので、３つのダミー変数$x_1,x_2,x_3$を用意します。この３つのダミー変数の組み合わせを各カテゴリに対応させます。例えば、A型：$x_1=0,x_2=0,x_3=0$、B型：$x_1=1,x_2=0,x_3=0$、O型：$x_1=0,x_2=1,x_3=0$、AB型：$x_1=0,x_2=0,x_3=1$
これらのダミー変数を用いた推定の結果得られた回帰係数は、$x_1=0,x_2=0,x_3=0$に対応づけたカテゴリを基準に他のカテゴリがどの程度異なるかを表しています。今回の血液型の例題では、目的変数を病気のリスクとして回帰分析を実施した時に次のような回帰式が得られたとする。

y = a + b_1x_1 + b_2x_2 + b_3x_3 +\epsilon

この場合、$a$がA型の病気リスクを表し、回帰係数$b_1,b_2,b_3$はそれぞれB型・O型・AB型の病気のリスクがA型からどれだけ異なっているかを表します。

4. 共分散分析

以前別の記事で分散分析について説明しましたが、３群以上の平均値の群間比較を実施する場合に分散分析を実施するんでしたよね。ただ２群の平均値群間比較にも分散分析は使用できます。その場合、２群の分散分析=2群間のt検定は同じことを指すことになります。
今回はt検定を用いて２群間の平均値比較を以下の例で実施したいと思います。

例題
会社A,Bの年収に差があるかを調査する。
A,B社のそれぞれの平均年収と標準偏差は次の表の通りであり、正規分布に従っているとする。
(正規分布からの乱数を発生させて、それを標本とすることで正規性の検定を省略できる）
下の表を見る限りそれぞれの会社の年収には違いがありそうですね。

実際にRで分析したコードと結果が次のようになる。

# A,B社それぞれ乱数を発生させる
A <- rnorm(30, 500, 50)
B <- rnorm(30, 550, 50)

# 乱数を標本とみなして、２標本の検定を実施
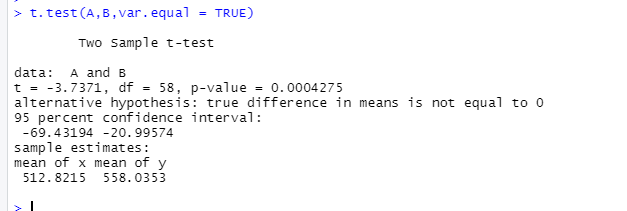
t.test(A,B,var.equal = TRUE)

p値が0.00042となり、有意水準5%のとき$p<\alpha$となるので帰無仮説を棄却して対立仮説を採択する。よってA社とB社の平均年収には差があると結論付けられる。

しかし本当に差があると結論付けてしまってもよいのでしょうか？

皆さんも各会社の平均年収を見るときに、平均年齢もみると思います。なぜなら年齢が高いほど年収も上がっていく傾向があるため。つまり平均年収が高くなる要因として２つの可能性が考えられます。

１．本当にその会社の給与水準が高い
２．その会社の社員平均年齢が高い

つまり先ほどの例でいうと、A社とB社の平均年収の差は本当に給与水準の違いによるものなのか、それとも社員の年齢が高いことによるものなのかを明らかにする必要があると思います。

このように通常の分散分析に使われるデータに対して、量的変数のデータを加えて分析をすることを共分散分析といいます。またその時の量的変数を共変量といいます。
この共分散分析のすごいところが、結果に影響を与える他のデータの影響を調整することができることです。今回の例でいうと、年収に影響を与えていると考えられる、年齢の影響を除いたA社とB社の比較ができるということです。

では実際に先ほどの例に平均年齢を加えたデータを使用して、共分散分析を実施してみたいと思います。
()内の数値が標準偏差を表しています。

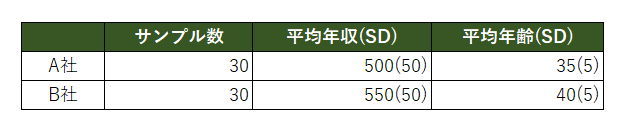
このデータを用いて共分散分析を実施したコードと結果が次のようになります。
(共分散分析はRよりもPythonのほうが簡単にできるので、Pythonで実施しました)

python

# ライブラリのインポート
import pandas as pd
from pingouin import ancova

# データの読み込み
df_workers = pd.read_csv("ancova.csv")

# 共分散分析の実行
result = ancova(data=df_workers, dv="money", covar="age", between="company")
print(result)

分析結果を見るとcompany行のp値を見ると、0.089となり有意水準5%のとき帰無仮説を棄却できない結果となりました。つまり年齢の影響を差し引いた会社のみの効果では、A社とB社の年収に差はないと結論付けられました。

ただし共分散分析を使うには２つの条件があります。
１．群間で回帰の傾きが異ならない、つまり回帰直線が平行になることです。言い換えると交互作用がないことを意味しています。交互作用の検定の結果有意でない場合、この条件をクリアするとします。
２．回帰係数が０ではない。回帰係数が０である場合は、共変量を含めず通常の分散分析を行います。これも傾きの有意性検定で有意である場合に条件クリアとなります。

5. 多重共線性

説明変数が複数個ある重回帰において、説明変数同士が強く相関している場合多重共線性があるといいます。そして多重共線性がある場合、回帰係数の推定誤差が大きくなる問題が起きやすくなります。つまり回帰係数の推定値の信頼性が落ちるということです。

多重共線性の度合いを測定するために、分散拡大係数：VIFを計算するようにしましょう。
VIFは各説明変数に対して値が算出され、１つの説明変数$x_i$を目的変数に設定し、残りの説明変数を用いて回帰しその決定係数を計算します。
説明変数$i$のVIF$_i$は、決定係数$R^2$を用いて次のように計算できます。

VIF_i = \frac{1}{1-R_i^2}

$VIF>10$であるような場合には、２つの間の相関は非常に強いことを表します。$VIF=10$とは相関係数でいうところの$0.95$程度とかなり強い相関を表しています。このような場合、２つの変数を両方入れた回帰モデルは避けるべきです。
強い多重共線性があると判明した場合は、簡潔な対処の１つとして相関しあう２つの変数のうち１つの除いてあげるとよいでしょう。また説明変数が多いとその分用意しないといけないサンプルデータも増えるので、説明変数はむやみやたらに増やさないようにしましょう。

では実際に例題を用いて重回帰分析から多重共線性までを通して行ってみたいと思います。

例題
社会人10名の年収に関して分析を実施してみたいと思います。
サンプルデータは次のようになります。

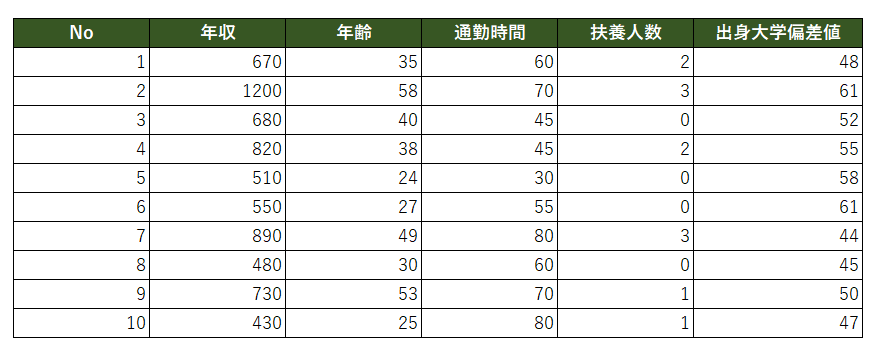
まずPythonで重回帰分析を実施しました。

Python

import pandas as pd
import statsmodels.api as sm

# csv読み込み
df = pd.read_csv("income.csv")

# 目的変数、説明変数の名前設定
y_col = "年収"
x_col = ["年齢", "通勤時間", "扶養人数", "出身大学偏差値"]

# 読み込んだdf内で目的変数、説明変数指定
x = df[x_col]
y = df[y_col]

# 重回帰分析
model = sm.OLS(y, sm.add_constant(x))
result = model.fit()

# 結果表示
print(result.summary())

出力結果

                            OLS Regression Results
==============================================================================
Dep. Variable:                     年収   R-squared:                       0.969
Model:                            OLS   Adj. R-squared:                  0.944
Method:                 Least Squares   F-statistic:                     38.68
Date:                Thu, 18 Aug 2022   Prob (F-statistic):           0.000593
Time:                        15:17:46   Log-Likelihood:                -50.790
No. Observations:                  10   AIC:                             111.6
Df Residuals:                       5   BIC:                             113.1
Df Model:                           4
Covariance Type:            nonrobust
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const       -220.3030    232.438     -0.948      0.387    -817.803     377.197
年齢            11.5330      2.119      5.443      0.003       6.086      16.980
通勤時間          -2.0274      1.598     -1.269      0.260      -6.135       2.080
扶養人数          94.0915     21.796      4.317      0.008      38.063     150.120
出身大学偏差値        9.3459      3.466      2.696      0.043       0.436      18.256
==============================================================================
Omnibus:                        0.672   Durbin-Watson:                   2.266
Prob(Omnibus):                  0.715   Jarque-Bera (JB):                0.343
Skew:                          -0.406   Prob(JB):                        0.842
Kurtosis:                       2.593   Cond. No.                     1.19e+03
==============================================================================

決定係数をみると0.944となっており、非常にこの回帰の精度が高いことを表している。また各偏回帰係数のp値は通勤時間以外は有意水準5%よりも小さい値なので、目的変数の変動にその説明変数の影響があると統計学的に判断できます。通勤時間は影響しているかどうか判断保留状態となります。

上記結果から得られた回帰式は

年収 = 年齢 \times 11.5 - 通勤時間 \times 2.0 + 扶養人数 \times 94.1 + 出身大学偏差値 \times 9.3 - 220.3

となることがわかります。つまり年齢30歳、通勤時間30分、扶養人数0人、出身大学偏差値50の人の年収は約530万円ほどと推測できます。続いてVIF統計量を計算します。今回はVIF統計量を計算するパッケージを用いましたが、計算自体は単純なので自ら関数を作成することもできます。

Python

# VIFを使用するためのパッケージ
from statsmodels.stats.outliers_influence import variance_inflation_factor as vif

# 説明変数だけのdfを作成
df_col = df.loc[:,x_col]

# 定数項を追加
df_col['Intercept'] = 1.0

# VIF計算。定数項は無視
for i in range(len(df_col.columns)-1):
    name = df_col.columns[i] #カラム名取得
    vif_val = vif(df_col.to_numpy(), i) #vif計算
    print(f'{name: <10}{vif_val}') #nameを左寄せで表示、vif_valの値表示

出力結果

年齢        1.9454318672280828
通勤時間      2.005168426589433
扶養人数      2.1388117076092312
出身大学偏差値   1.451144533976667

よって今回はVIF統計量が10を超える変数はなかったので変数間での相関関係はほぼないと判断できます。

6. 二元配置の分散分析

線形回帰モデルは、ある説明変数$x_i$は他の説明変数とは独立に、1増えるごとに$b_i$だけ目的変数が変化することを仮定していました。ただ実際のデータにおいては、$x_i$が１増えたときの$y$の増え方が、他の説明変数に影響される場合も考えられます。このような説明変数同士の相乗効果を交互作用といいます。線形回帰モデルの中に掛け算$cx_ix_j$として導入することができます。例えば説明変数が２つで、交互作用のある線形回帰モデルは$y=a+b_1x_1+b_2x_2+cx_1x_2+\epsilon$となります。

しかし線形回帰モデルの中に交互作用項を入れるかどうかは多くの統計ユーザが迷う箇所でもあります。よって交互作用項を回帰モデルに入れるかどうかの判断は次のような時に限ってのみ導入するようにしましょう。
・データから明らかに交互作用がある場合
・交互作用の有無に興味がある場合
ここでは一旦交互作用という言葉さえ覚えてもらえば十分です。

話は変わりますが、以前別の記事で紹介した、３群間以上の平均値を比較する手法として分散分析がありました。その際は１つの要因について分析していたため、一元配置の分散分析でしたが、複数の要因を同時に考えて多元配置の分散分析を実施することも可能です。説明変数が複数ある場合は、交互作用についても考えることができます。

例えば前回の一元配置分散分析で使用した例題に要因を１つ追加して、茎の長さ(目的変数)に対し１つ目の要因(説明変数$x_1\ $)を肥料のなし/あり、２つ目の要因(説明変数$x_2$)を温度の低い/高いとして、これらの要因が茎の長さに影響を与えているかを考えます。交互作用を考慮しないモデルであれば、肥料の聞き方は温度に依存しませんし、温度変化の影響も肥料の有無に依存しません。しかし現実の現象では、肥料の効き方は温度によって変化する可能性もあります。その場合は交互作用項をいれて分散分析を実施するとよいでしょう。

こちらに関しては例題などは長くなるので省略させていただきます。

1-9 統計学基礎～一般化線形モデル1