1-10 統計学基礎～一般化線形モデル2

はじめに

1-9の記事に引き続き一般化線形モデルについて説明していきます。
主に一般化線形モデルの考え方や統計モデルの評価について説明していけたらと思ってます。

目次

1. 一般化線形モデルとは
2. 尤度と最尤法
3. ロジスティック回帰
4. ポアソン回帰
5. 一般化線形モデルの使い分け
6. Wald検定
7. 尤度比検定
8. AIC/BIC

1. 一般化線形モデルとは

ここまでの記事で最小二乗法を用いてパラメータを推定することを考えてきました。この枠組みを説明変数が量的変数である重回帰から、説明変数がカテゴリ変数である分散分析までを含み一般線形モデルといいます。一般線形モデルの枠組みを広げて、最小二乗法ではなく確率分布に基づいた最尤法という手法を用いて回帰モデルを推定するモデルを一般化線形モデル:GLMといいます。

2. 尤度と最尤法

最小二乗法では回帰モデルとデータ間の差(残差)に二乗を計算し、最小化することでパラメータを求めました。しかし二値変数である目的変数のデータや非負整数である目的変数データでは、ほとんど同じ値をとる領域や値が大きくばらつく領域があったりするため最小二乗法による推定向いていません。そのため距離をもとにモデルとデータの適合度を測定するよりも、データが確率的に生成されたことを考え、確率的な起こりやすさをもとにデータへの当てはまりのよさを評価するとよさそうです。

ここで手元にあるデータ$x(x_1,x_2,・・・,x_n)$、確率分布のパラメータ$\theta$と表記すると、データ$x$があるパラメータ$\theta$の確率分布からどの程度起きやすいかを次のように書けます。

P(x|\theta) = P(x_1|\theta) \times P(x_2|\theta) \times・・・\times P(x_n|\theta)

$P(x|\theta) $をデータ$x$に対してパラメータ$\theta$の関数としてみたものを、尤度といいます。
つまり手元のデータ$x$に対し$\theta$を変えることで、尤度が変化するイメージです。尤度が大きいということは、その$\theta$で手元のデータが起きやすいことを表しています。つまり尤度を最大化する$\theta$を見つけ、推定値とすれば、手元のデータへもっとも当てはまる$\theta$を得ることができます。この手法を最尤法または最尤推定といいます。

一般化線形モデルは、目的変数の誤差の確率分布を指定し、尤度に基づいてパラメータを推定する回帰です。線形回帰で通常仮定される正規分布の誤差を持つモデルに対して、最小二乗法を用いてパラメータ推定を実施した結果と最尤法を用いて推定した結果は同じになります。

ではここで尤度と最尤法についてのイメージをつかむために簡単な例題を考えてみたいと思います。
例題
コインが１枚ある。このコインは偏りがあるらしく表の出る確率が1/2ではありません。ここで表の出る確率を調べるために、コインを10回投げたところ8回表が出ました。このときコインの表が出る確率はいくつになるか考えます。

最尤推定は、手元のデータがどの母集団パラメータに従う確率分布から得られる確率が最も高いかに基づいて考える推定方法です。「10回中8回表が出た」というデータが、表が出る確率がいくつのときに最も得られる確率が高いかを考えます。

１．表の出る確率が1/2のとき、10回中8回表が出る確率
　$_{10}C_8(1/2)^8(1/2)^2 = 0.0439 \ $

２．表が出る確率が2/3のとき、10回中8回表が出る確率
　$_{10}C_8(2/3)^8(1/3)^2 = 0.195 \ $

３．表が出る確率が3/4のとき、10回中8回表が出る確率
　$_{10}C_8(3/4)^8(1/4)^2 = 0.282 \ $

４．表が出る確率が4/5のとき、10回中8回表が出る確率
　$_{10}C_8(4/5)^8(1/5)^2 = 0.302 \ $

５．表が出る確率が5/6のとき、10回中8回表が出る確率
　$_{10}C_8(5/6)^8(1/6)^2 = 0.291 \ $

このように計算をしたとき、10回中8回表が出る確率というデータが得られる確率が最も高くなったのが$4/5$のときである。
よって$4/5$が最尤推定量になります。

3. ロジスティック回帰

一般化線形モデルの１つであるロジスティック回帰について紹介します。ロジスティック回帰は、目的変数が二値のカテゴリ変数である場合に使用される回帰です。例えば、目的変数がアンケートのYes/Noや生存/死亡などです。カテゴリの１つが起こる確率を$p$とすると、ロジスティック回帰は説明変数$x$を変えたときに、$p$がどのように変化するかを調査する回帰です。

予測したい事象(正事象という）が起こる確率を$p$とし、オッズ(正事象の起こりやすさの指標)を$p/(1-p)$と表す。
ロジスティック回帰では、このオッズの対数を説明変数$x_i$の線形和で次のように表現する。

\log\left(\frac{p}{1-p} \right) = a + b_1x_1 + b_2x_2 +・・・+b_nx_n

左辺のオッズの対数を取ったものをロジット関数といいます。また右辺の線形和を線形予測子といいます。今回求めたいのは正事象の確率$p$なので、上記式を$p$について変形すると次の式が得られます。

p = \frac{1}{1 + \exp[-(a + b_1x_1 + b_2x_2 +・・・+b_nx_n)]} \\

この関数をロジスティック関数といい、$a + b_1x_1 + b_2x_2 +・・・+b_nx_n$を0から1の範囲に変換する働きを持っています。
上式における回帰係数を最尤推定法によって最適化することで、正事象を求めることができます。

ロジスティック回帰の結果に対して、オッズ比という値を用いて評価することがあります。先ほども少しお話ししましたが、ある事象が起こる確率$p$に対して、起こらない確率$1-p$との比である$p/(1-p)$をオッズといいます。
オッズは確率$p(0 \leq p \leq 1)$を、$0 \leq オッズ \leq \infty$の範囲に変換した値だと考えるとよいでしょう。競馬などのギャンブルで使われているオッズと同じものです。

また２つの確率$p,q$に対し、２つのオッズの比をオッズ比といいます。

OR = \frac{(p/(1-p))}{(q/(1-q))}

オッズ比が１より大きい場合、確率$p$のほうが確率$q$よりも起きやすいことを表します。逆もしかりです。
例えば、風邪薬を飲む場合３日以内に治る確率$p=0.8$、飲まない場合３日以内に治る確率$p=0.4$とすると、オッズ比は$(0.8/0.2)/(0.4/0.6)=6$となる。つまり１より大きいので、風邪薬を飲む場合に３日以内に治るほうが起きやすいと判断できる。ここで１点注意なのは、オッズ比が6だからといって６倍起こりやすいと解釈してはいけない。

4. ポアソン回帰

負の値を取らない整数値、特にカウント数が目的変数である場合に候補となる一般化線形モデルがポアソン回帰です。例えば目的変数が１つの木に咲く花の数の場合、負の値をとることはありませんし、整数値で表されるためポアソン回帰の候補になります。ポアソン回帰は、目的変数の誤差項がポアソン分布に従う回帰です。ポアソン回帰における説明変数$x_i$と目的変数$y_i$は、パラメータ$\lambda_i$を通して次のような関係があります。

y_i \sim Poisson(\lambda_i) \\
\lambda_i = \exp(a+bx_i)

この場合のリンク関数は両辺の対数をとった、$\log(\lambda)$であることがわかります。

ここでポアソン分布について簡単に説明したいと思います。
単位時間当たり平均$\lambda$回起こる事象がちょうど$k$回起こる確率は

P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}

とかける。これをポアソン分布という。ポアソン分布の平均分散はどちらも$\lambda$となるので、平均と分散は独立ではないという特徴があります。ここで１つ具体例を考えてみたいと思います。

例題
1時間に平均5回再生される動画がとある１時間に10回再生される確率を求めろ。

P(X=10) = \frac{5^{10} e^{-5}}{10!} = 0.018(約1.8\%)

他にもコールセンターや１日の事故数などもポアソン分布で計算することができます。簡単ではありますが、説明は以上にします。ポアソン分布の確率関数がなぜ上記のような形で表されるのか？などについては興味のある方はネットで調べてみてください。(二項分布の極限をとるとポアソン分布になある)

5. 一般化線形モデルの使い分け

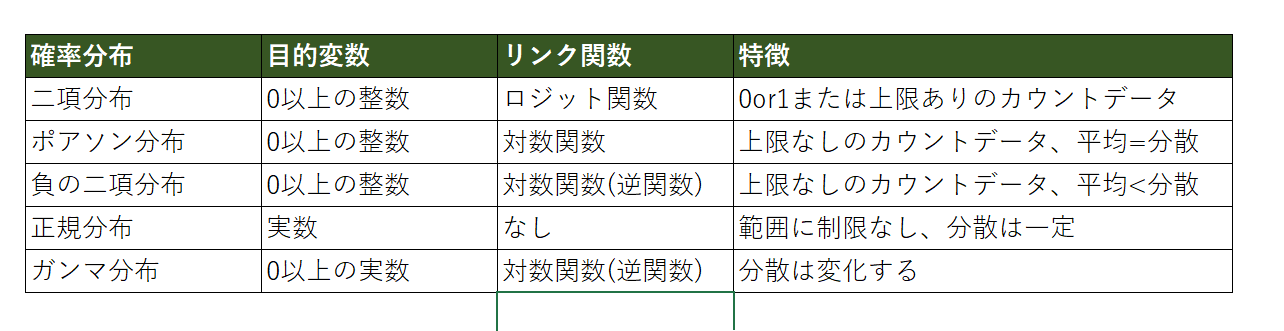
ここまでロジスティック回帰とポアソン回帰について紹介しましたが、他にも負の二項分布を誤差分布とした負の二項回帰やガンマ分布を誤差分布としたガンマ回帰があります。ここでは紹介を省きますが、特徴は以下の表にまとめておきます。
またリンク関数とは線形予測子とイコールになる関数のことです。つまり次のような関係。

f(z) = a + bx

上記表を参考にデータや目的変数の形から次の３つを決めます。
１．確率分布
２．リンク関数
３．線形予測子
３つを設定した後は最尤推定法を用いてパラメータを推測しモデルを作成し、その後作成したモデルの評価を実施します。これがGLMの大まかな流れになっています。
いくつか例題を試しに実施したいのですが、一旦統計モデルの評価方法について説明した後とさせていただきます。

6. Wald検定

線形回帰モデルと同様に、一般化線形モデルにおいても推定した回帰係数に関する仮説検定を次の条件で実行できます
帰無仮説：回帰係数$=0$
対立仮説：回帰係数$\neq 0$
推定値のばらつきを表す標準誤差を用いて、最尤推定で得られた推定値/標準誤差をWald統計量といいます。
最尤推定量が正規分布に従うと仮定すれば、Wald統計量を用いて信頼区間やp値を計算できます。この検定手法をWald検定といいます。ただサンプルサイズが大きくない場合には正規分布に従うという仮定が怪しくなりますので、次に紹介する尤度比検定を使ったほうが良いです。

7. 尤度比検定

最尤推定で得られた統計モデルを比較する方法として、データへの当てはまりがどれだけ改善されたかに基づく尤度比検定があります。
尤度比検定は比較する２つのモデルの内、片方がもう一方をネストしている関係である必要があります。例えば、モデル１：$y=a$とモデル２：$y=a+bx$の場合、モデル２はモデル１を含んでいるので尤度比検定が使えます。

この例では
帰無仮説：$y=a$(つまりb=0)
対立仮説：$y=a+bx$
となります。それぞれのモデルで最尤推定を実行すると、最大尤度$L_1, L_2$が得られます。この比を取った値の対数を取り、-2を掛けた値である次を検定統計量とします。

\Delta D_{1,2} = -2 \times (\log L_1 - \log L_2)

$\Delta D_{1,2}$が大きいほど帰無仮説に比べて対立仮説の尤度が大きく当てはまりが改善していることになります。

8. AIC/BIC

統計モデルを比較するための他の手法として、情報量基準に基づくモデル選択があります。情報量基準にはいくつか種類がありますが、最も有名なのがAIC：Akaike Information Criterion;赤池情報量基準となっています。
AICは新たに得られるデータの予測の良さをもとに、モデルの良さを決める指標です。モデルの最大尤度をL、モデルのパラメータ数をkとして次のように計算されます。

AIC = -2 \log L + 2k

分析者が用意したいくつかの候補モデルの中で、AICを最小化するモデルを良いモデルとして選択するとよいでしょう。AICは手元のデータへの当てはまりの良さだけでなく、モデルのパラメータ数でペナルティをつけてモデルを選ぶことで過剰適合しないモデルを選択する指標です。
過剰適合とは手元のデータに過剰に当てはめてしまい、新たに得られるデータをうまく表さない状態のことです。
最後に１点AICの注意点として、AICは新しく得られるデータの予測精度を高くするモデルを選ぶという目的の指標であるため、AICの最小化によってデータを生成した分布を表す真のモデルが必ずしも選ばれるわけではありません。

他によく使用される情報量基準には、BIC:Bayesian Informaiton Criterion;ベイズ情報量基準があります。BICは最大尤度をL、パラメータ数k,サンプルサイズnとして次のように計算されます。

BIC = -2 \log L + k \log(n) \\

この値を最小化するモデルを良いモデルとします。AICと同じように尤度が大きいほどBICは小さくなります。BICは候補として用意した統計モデルに対し、真のモデルである確率が高いモデルが良いモデルであるという観点で導出されます。