three.jsの公式チュートリアルCreating a sceneではBoxGeometryを使って立方体を描いています。
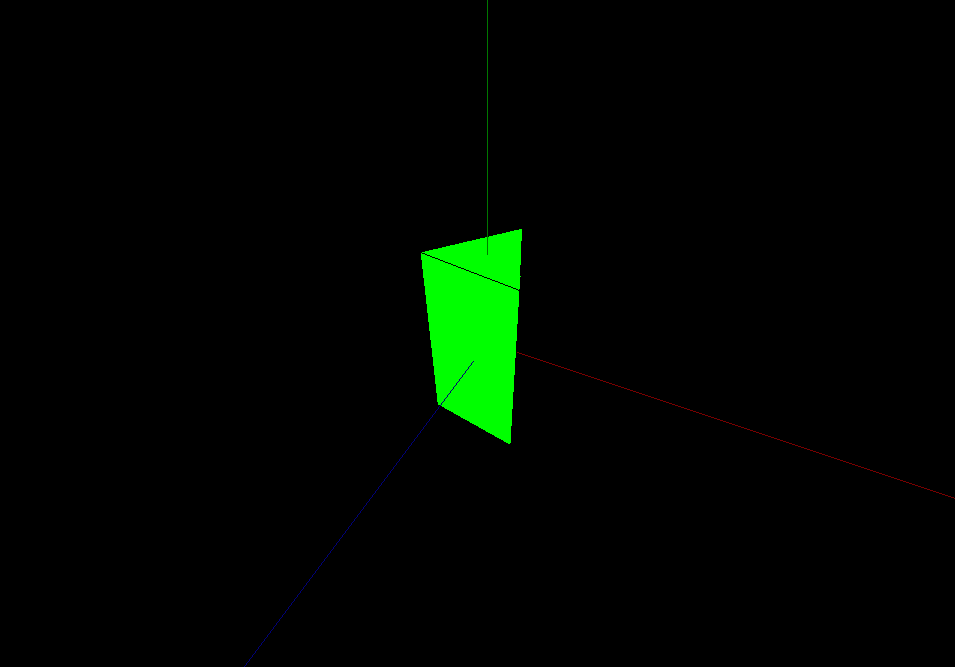
もっと基本的なクラスであるGeometryクラスを使い、正三角柱を作ってみました。
正三角柱の中心(底面の正三角形の重心、かつ側面の高さ半分のところ)に座標原点が来るようにしました。
EdgesGeometryを利用して、ジオメトリのワイヤフレーム(辺)を黒い線で描いています。
また、座標軸を赤緑青で描いています。
<!DOCTYPE html>
<html>
<head>
<meta charset=utf-8>
<title>My first three.js app</title>
<style>
body { margin: 0; }
canvas { width: 100%; height: 100% }
</style>
</head>
<body>
<script src="js/three.js"></script>
<script>
var scene = new THREE.Scene();
var camera = new THREE.PerspectiveCamera(75, window.innerWidth / window.innerHeight, 0.1, 1000);
var renderer = new THREE.WebGLRenderer();
renderer.setSize(window.innerWidth, window.innerHeight);
document.body.appendChild(renderer.domElement);
// 三角柱をつくる。原点は底面正三角形の重心、柱の高さの半分の位置とする。
// length: 底面の正三角形の辺の長さ
// height: 三角柱の高さ
function createTriangle(length, height)
{
var faceColor = 0x00ff00;
var halfHeight = height / 2.0;
var halfLength = length / 2.0;
// 正三角形の重心から辺へ下ろした垂線の長さ
var distanceToLine = halfLength * Math.tan(Math.PI / 6.0);
// 正三角形の頂点から対辺へ垂線を下ろしたときの、垂線と重心の間の距離
var distanceFromVertex = halfLength / Math.tan(Math.PI / 6.0) - distanceToLine;
var vertices = [
new THREE.Vector3(-halfLength, halfHeight, distanceToLine), // 上面の三角形の頂点
new THREE.Vector3(0, halfHeight, -distanceFromVertex),
new THREE.Vector3(halfLength, halfHeight, distanceToLine),
new THREE.Vector3(-halfLength, -halfHeight, distanceToLine), // 下面の三角形の頂点
new THREE.Vector3(0, -halfHeight, -distanceFromVertex),
new THREE.Vector3(halfLength, -halfHeight, distanceToLine),
];
var faces = [
new THREE.Face3(0, 2, 1), // 上面
new THREE.Face3(3, 4, 5), // 下面
new THREE.Face3(0, 3, 2), // 手前側面
new THREE.Face3(2, 3, 5),
new THREE.Face3(0, 1, 3), // 左側面
new THREE.Face3(1, 4, 3),
new THREE.Face3(2, 5, 4), // 右側面
new THREE.Face3(4, 1, 2),
];
var geometry = new THREE.Geometry();
var i = 0;
for (i = 0; i < vertices.length; i++) {
geometry.vertices.push(vertices[i]);
}
for (i = 0; i < faces.length; i++) {
geometry.faces.push(faces[i]);
}
var material = new THREE.MeshBasicMaterial({ color: faceColor });
// 三角柱のワイヤーフレームを描く
var wireframeGeometry = new THREE.EdgesGeometry(geometry);
var wireframeMaterial = new THREE.LineBasicMaterial({ color: 0x000000, linewidth: 2 });
var triangleMesh = new THREE.Mesh(geometry, material);
var wireframe = new THREE.LineSegments(wireframeGeometry, wireframeMaterial);
triangleMesh.add(wireframe);
return triangleMesh;
}
// x, y, z軸を赤、緑、青で描く
// length: 軸の長さ
function createAxes(length)
{
var createOneAxis = function (color, vertex) {
var material = new THREE.LineBasicMaterial({
color: color
});
var vertices = [
new THREE.Vector3(0, 0, 0),
vertex
];
var geometry = new THREE.Geometry();
geometry.vertices = vertices;
var line = new THREE.Line(geometry, material);
return line;
};
return [
createOneAxis(0x770000, new THREE.Vector3(length, 0, 0)),
createOneAxis(0x007700, new THREE.Vector3(0, length, 0)),
createOneAxis(0x000077, new THREE.Vector3(0, 0, length))
];
}
var mesh = createTriangle(10, 20);
scene.add(mesh);
var axes = createAxes(100);
axes.forEach(function (a) { scene.add(a);})
camera.position.z = 30;
camera.position.y = 30;
camera.position.x = 15;
camera.lookAt(0, 0, 0);
function animate() {
requestAnimationFrame(animate);
//mesh.rotation.x += 0.01;
mesh.rotation.y += 0.01;
renderer.render(scene, camera);
}
animate();
</script>
</body>
</html>
上記を適当な名前のhtmlとして保存し、ブラウザで開くとこのように表示されます。
正三角柱はY軸(緑)のまわりを回転します。