こちらの記事は、2019年 8月に公開された『 Data Scientists, The 5 Graph Algorithms that you should know』の和訳になります。
本投稿は転載であり、本記事はこちらになります。
はじめに
私たちデータサイエンティストは、Pandas、SQL、他のどんなリレーショナルデータベースに対しても、かなり満足しています。
私たちは、ユーザーの属性を列で表現し、ユーザを行として並べることに見慣れています。
しかし、現実の世界は本当にそのようになっているでしょうか?
コネクテッドワールドでは、ユーザーを独立したエンティティと見なすことはできません。
ユーザーはお互いが一定の繋がりをもっているため、機械学習モデルを構築するときに、関係性を含めたい場合があります。
リレーショナルデータベースでは、異なる行(ユーザー)の間でこのような関係性を使用することはできませんが、グラフデータベースでは非常に簡単に使用できます。
この記事では、知っておくべき最も重要なグラフアルゴリズムと、Pythonでの実現方法をいくつか説明します。
また、CourseraでUCSANDiegoが提供しているビッグデータのグラフ分析コースでグラフ理論の基礎を学ぶことを強くお勧めします。
1.連結成分(Connected Components)
クラスタリングの仕組みを知っていますか?
連結成分は、ごく一般的な用語で、関連/接続されたデータ内のクラスター/アイランドを見つける一種のハードクラスタリングアルゴリズムと考えることができます。
例えば、世界中の2つの都市を結んでいる任意の道路のデータを持っていて、そこからすべての大陸と、大陸にどの都市が含まれるのか探り当てたいとします。
どうやって実現しますか?考えてみてください。
これを行うために使用する連結成分アルゴリズムは、BFS / DFS の特殊なケースに基づいています。
ここではどのように機能するかについてはあまり説明しませんが、Networkxを使用してコードを起動して実行する方法について説明します。
用途
小売業の観点:多くの顧客がいて、多くのアカウントを使用しているとしましょう。私たちは、Connected Componentsアルゴリズムを使用して、データセット内の異なるグループを見つけることができます。
クレジットカードの使い方、住所または携帯電話番号などが同じだということに基づいて辺(エッジ)を推定することができます。
一度これらのつながりがわかれば、グループIDを割り当てるクラスタを作成するために連結成分アルゴリズムを実行することができます。
そうすると、このグループIDを使用して、各グループのニーズにあった推奨事項を提供できます。
また、グループIDを使用して、グループごとの特徴を作成し、分類アルゴリズムを強化することもできます。
財務の観点:別のユースケースは、これらのグループIDを使用して詐欺を見つけることです。
アカウントが過去に不正を行った場合、繋がりがあるアカウントも不正を行う可能性が高いです。
あなたの想像力次第で、用途の可能性は無限大です。
コード
Networkxグラフの作成と分析にPython のモジュールを使用します。
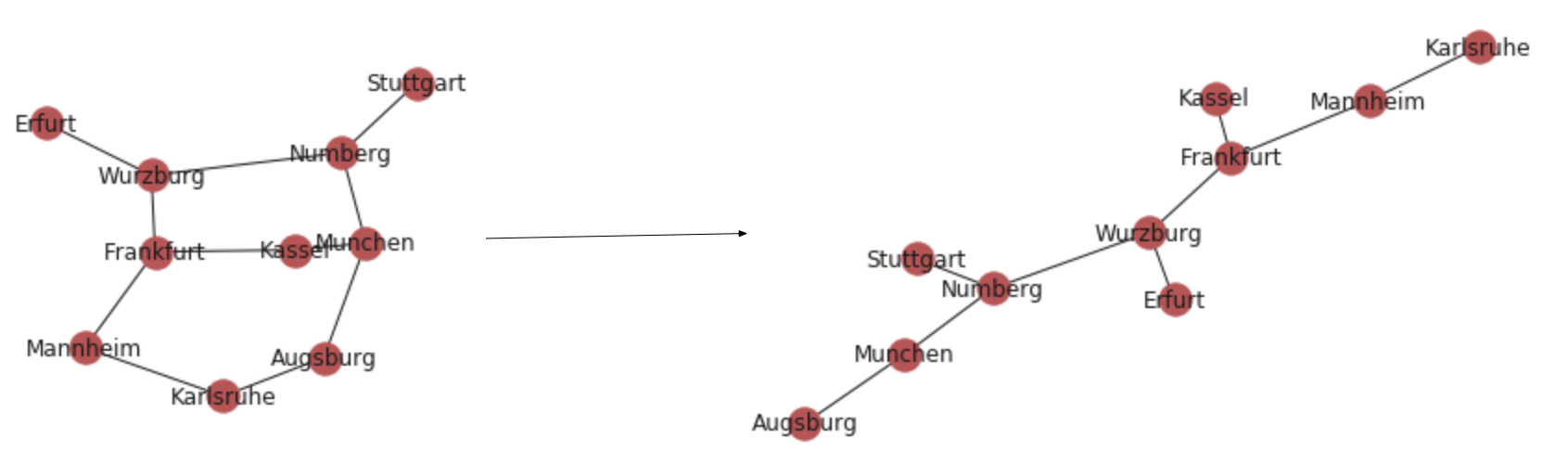
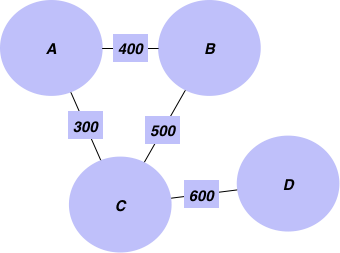
目的を達成するために使うグラフの例から始めましょう。都市とそれらの間の距離情報が含まれています。
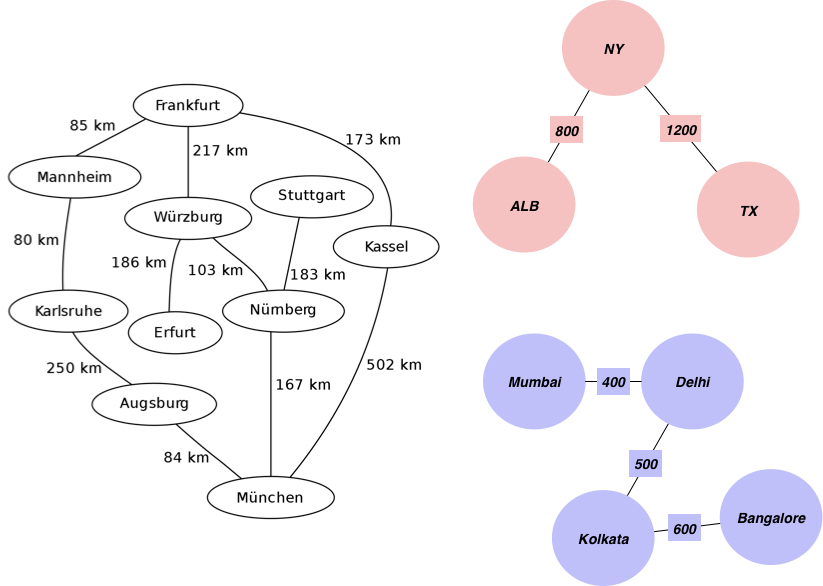
まず、辺の重みとして追加する距離と辺のリストを作成することから始めます。
edgelist = [['Mannheim', 'Frankfurt', 85], ['Mannheim', 'Karlsruhe', 80],
['Erfurt', 'Wurzburg', 186], ['Munchen', 'Numberg', 167],
['Munchen', 'Augsburg', 84], ['Munchen', 'Kassel', 502],
['Numberg', 'Stuttgart', 183], ['Numberg', 'Wurzburg', 103],
['Numberg', 'Munchen', 167], ['Stuttgart', 'Numberg', 183],
['Augsburg', 'Munchen', 84],['Augsburg', 'Karlsruhe', 250],
['Kassel', 'Munchen', 502], ['Kassel', 'Frankfurt', 173],
['Frankfurt', 'Mannheim', 85], ['Frankfurt', 'Wurzburg', 217],
['Frankfurt', 'Kassel', 173], ['Wurzburg', 'Numberg', 103],
['Wurzburg', 'Erfurt', 186], ['Wurzburg', 'Frankfurt', 217],
['Karlsruhe', 'Mannheim', 80], ['Karlsruhe', 'Augsburg', 250],
["Mumbai", "Delhi",400],["Delhi", "Kolkata",500],
["Kolkata", "Bangalore",600],["TX", "NY",1200],
["ALB", "NY",800]]
Networkxを使用してグラフを作成しましょう
g = nx.Graph()
for edge in edgelist:
g.add_edge(edge[0],edge[1], weight = edge[2])
次に、このグラフから異なる大陸とその都市を見つけ出します。
connected componentsアルゴリズムを使用することができます:
for i, x in enumerate(nx.connected_components(g)):
print("cc"+str(i)+":",x)
------------------------------------------------------------
cc0: {'Frankfurt', 'Kassel', 'Munchen', 'Numberg', 'Erfurt',
'Stuttgart', 'Karlsruhe', 'Wurzburg', 'Mannheim', 'Augsburg'}
cc1: {'Kolkata', 'Bangalore', 'Mumbai', 'Delhi'}
cc2: {'ALB', 'NY', 'TX'}
このように、データ内の個別の成分を見つけることができます。エッジと頂点を使用するだけです。異なるデータでこのアルゴリズムを実行して前述したユースケースを満たすことができます。
2.最短経路
上記の例を続けるだけで、ドイツの都市とそれぞれの距離を示すグラフを作ることができます。
最短距離をとって、フランクフルト(出発ノード)からミュンヘンへの行き方を調べたいと思います。
この問題に使用するアルゴリズムは、ダイクストラ法と呼ばれます。ダイクストラ自身の言葉で次のように語られています:
ロッテルダムからフローニンゲンに移動する最短経路:
一般的には特定の都市から特定の都市へ移動するということは、最短パスのアルゴリズムであり、約20分で設計しました。ある朝、私はアムステルダムで若い婚約者と買い物をして疲れていました。私はコーヒーを飲むためにカフェテラスに座って最短経路のアルゴリズムを設計しました。先ほど言ったように、20分の発明でした。3年後の1959年に公開されました。この発表は読みやすく、非常に素晴らしいものです。優れたものになった理由の1つは、鉛筆と紙なしでデザインしたことです。鉛筆と紙なしでデザインしたため、回避可能な複雑さをすべて避けることができることが後になってわかりました。驚いたことに、このアルゴリズムは私の名声の礎石の1つになりました。
— Edsger Dijkstra、ACMコミュニケーションズ、2001年のフィリップL.フラナとのインタビュー
用途
・最短ルートを見つけるために、ダイクストラアルゴリズムの一種がGoogleマップで広く使用されています。
・ウォルマートストアでは、すべての通路の間に異なる距離の通路があるため、通路 Aから通路 Dに移動する最短経路を顧客に提供したいと考えるでしょう。
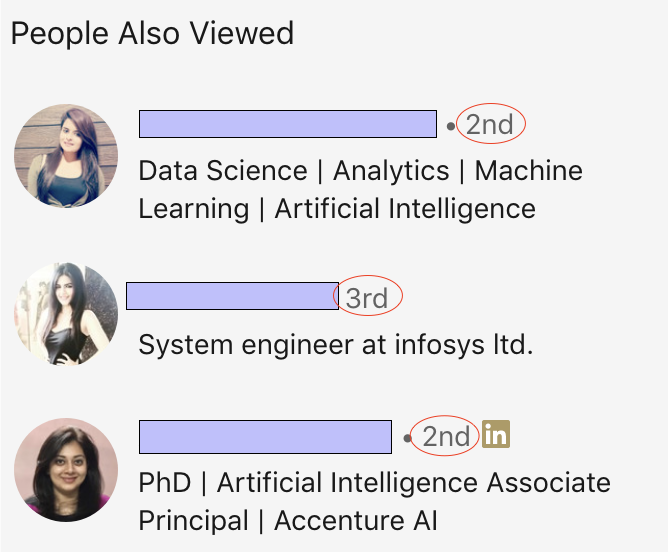
・LinkedInでは一次的なつながりと二次的なつながりなど、つながりの度合いを表示しています。表示するために裏側で何が起こっているのでしょうか?
コード
print(nx.shortest_path(g, 'Stuttgart','Frankfurt',weight='weight'))
print(nx.shortest_path_length(g, 'Stuttgart','Frankfurt',weight='weight'))
次の方法で、すべてのペア間の最短パスを見つけることができます。
for x in nx.all_pairs_dijkstra_path(g,weight='weight'):
print(x)
--------------------------------------------------------
('Mannheim', {'Mannheim': ['Mannheim'],
'Frankfurt': ['Mannheim', 'Frankfurt'], 'Karlsruhe': ['Mannheim', 'Karlsruhe'],
'Augsburg': ['Mannheim', 'Karlsruhe','Augsburg'],
'Kassel': ['Mannheim', 'Frankfurt', 'Kassel'],
'Wurzburg': ['Mannheim', 'Frankfurt', 'Wurzburg'],
'Munchen': ['Mannheim', 'Karlsruhe', 'Augsburg', 'Munchen'],
'Erfurt': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Erfurt'],
'Numberg': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Numberg'],
'Stuttgart': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Numberg', 'Stuttgart']})
('Frankfurt', {'Frankfurt': ['Frankfurt'],
'Mannheim': ['Frankfurt', 'Mannheim'],
'Kassel': ['Frankfurt', 'Kassel'], 'Wurzburg': ['Frankfurt', 'Wurzburg'],
'Karlsruhe': ['Frankfurt', 'Mannheim', 'Karlsruhe'],
'Augsburg': ['Frankfurt', 'Mannheim', 'Karlsruhe', 'Augsburg'],
'Munchen': ['Frankfurt', 'Wurzburg', 'Numberg', 'Munchen'],
'Erfurt': ['Frankfurt', 'Wurzburg', 'Erfurt'],
'Numberg': ['Frankfurt', 'Wurzburg', 'Numberg'],
'Stuttgart': ['Frankfurt', 'Wurzburg', 'Numberg', 'Stuttgart']})
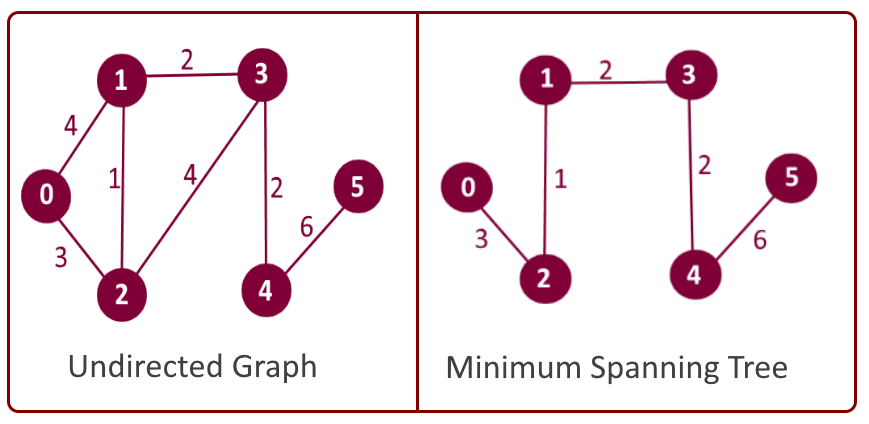
3.最小スパニングツリー(Minimum Spanning Tree: MST)
今度は別の問題です。私たちは水道管敷設会社またはインターネットの設備会社で働いています。 最小限のワイヤ/パイプを使用して、グラフ内のすべての都市を接続する必要があります。どうやって実現するのでしょうか?
用途
最小スパニングツリーは、コンピューターネットワーク、通信ネットワーク、運送ネットワーク、給水ネットワーク、および送電網(最初に発明された)を含むネットワークの設計に直接適用されます。
・MSTは巡回セールスマン問題の近似に使用されます。
・クラスタリング—最初にMSTを構築してから、クラスター間距離とクラスター内距離を使用してMSTの一部のエッジを分割するためのしきい値を決定します。
・画像セグメンテーション—ピクセルをノードとして、類似性の尺度(色、強度など)をピクセル間の距離としてグラフ上にMSTを構築する画像セグメンテーションに使用されました。
コード
# nx.minimum_spanning_tree(g) returns a instance of type graph
nx.draw_networkx(nx.minimum_spanning_tree(g))
4.ページランク
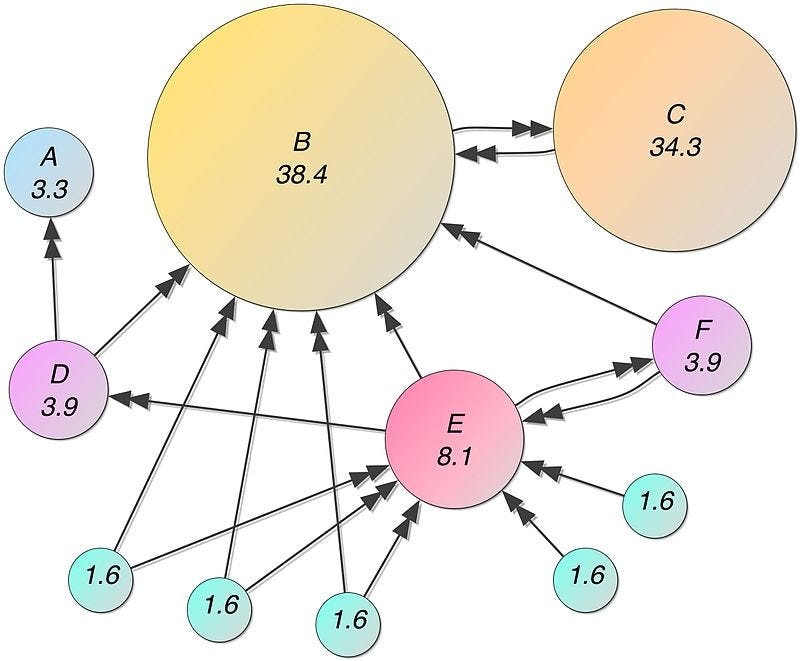
これは、Googleに長い間使用されているページソートアルゴリズムです。入力リンクと出力リンクの数と品質に基づいてページにスコアを割り当てます。
用途
ページランクは、ネットワーク内のノードの重要度を推定する任意の場所で使用できます。
・引用を使って、最も影響力のある論文を見つけるために使用されています。
・Googleがページのランキングに使用しています。
・ツイート-ユーザーおよびツイートをランク付けするために使用できます。ユーザーAがユーザーBをフォローしている場合はユーザー間のリンクを作成し、ユーザーがツイートをツイート/リツイートする場合はユーザーとツイート間のリンクを作成します。
・レコメンドエンジンとして使用されています。
コード
この例では、私たちが持っているFacebookユーザー間のエッジ/リンクのファイルをもとに、Facebookのデータを利用します。まず、以下を使用してFacebookのグラフを作成します。
# reading the dataset
fb = nx.read_edgelist('../input/facebook-combined.txt', create_using = nx.Graph(), nodetype = int)
次のようにして可視化します:
pos = nx.spring_layout(fb)
import warnings
warnings.filterwarnings('ignore')
plt.style.use('fivethirtyeight')
plt.rcParams['figure.figsize'] = (20, 15)
plt.axis('off')
nx.draw_networkx(fb, pos, with_labels = False, node_size = 35)
plt.show()
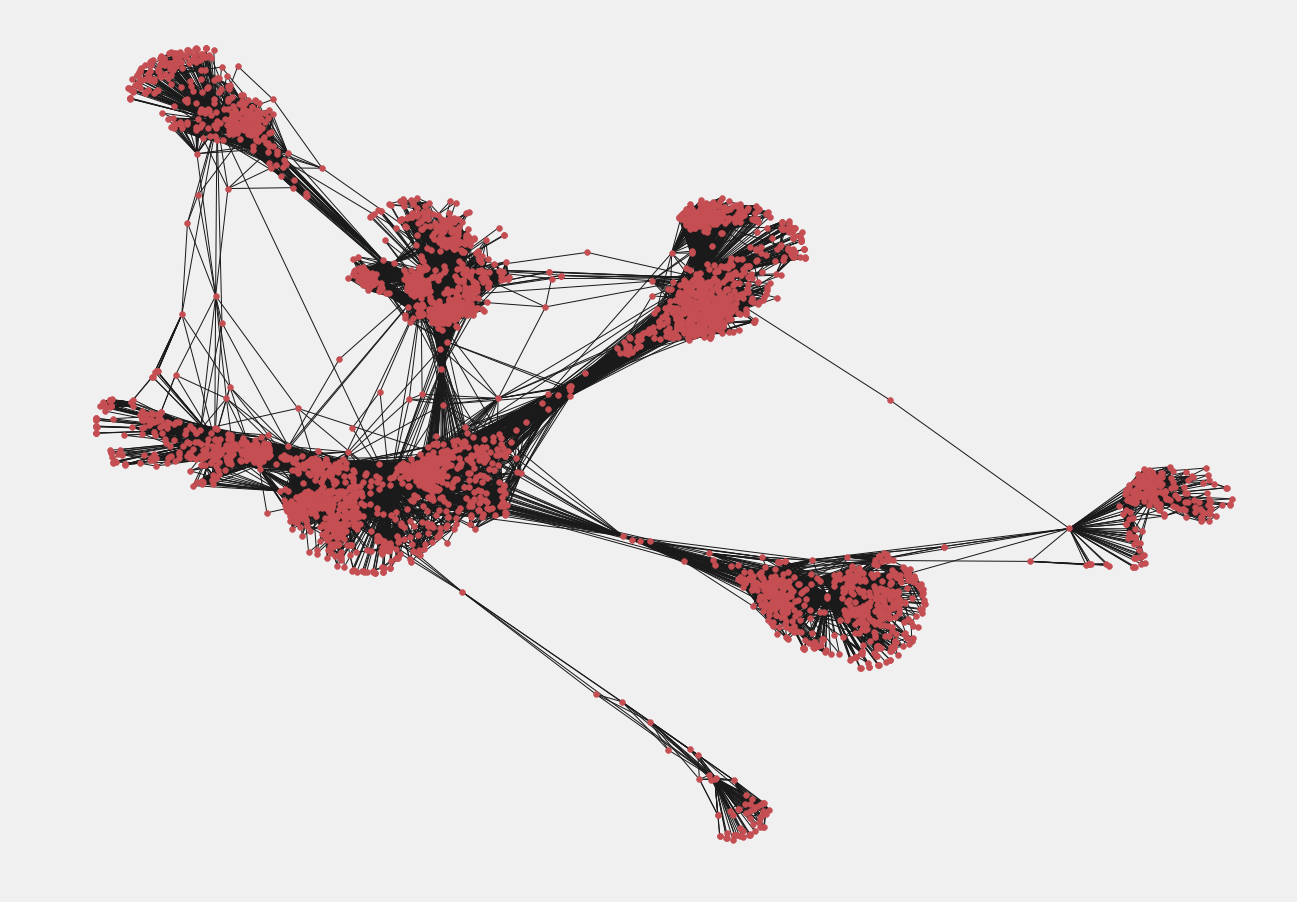
次に、影響力の高いユーザーを探します。
直観的には、ページランクアルゴリズムは「友達が多い友達」が多いユーザーに高いスコアを与えます。
pageranks = nx.pagerank(fb)
print(pageranks)
次の方法で、最も影響力のあるユーザー(ソートされたページランク)を取得できます。
import operator
sorted_pagerank =
sorted(pageranks.items(), key=operator.itemgetter(1),reverse = True)
print(sorted_pagerank)
------------------------------------------------------
[(3437, 0.007614586844749603), (107, 0.006936420955866114),
(1684, 0.0063671621383068295), (0, 0.006289602618466542),
(1912, 0.0038769716008844974), (348, 0.0023480969727805783),
(686, 0.0022193592598000193), (3980, 0.002170323579009993),
(414, 0.0018002990470702262), (698, 0.0013171153138368807),
(483, 0.0012974283300616082), (3830, 0.0011844348977671688),
(376, 0.0009014073664792464), (2047, 0.000841029154597401),
(56, 0.0008039024292749443), (25, 0.000800412660519768),
(828, 0.0007886905420662135), (322, 0.0007867992190291396),......]
上のIDはもっとも影響のあるユーザーです。
私達はもっとも影響のあるユーザーの部分グラフをみることができます。
first_degree_connected_nodes = list(fb.neighbors(3437))
second_degree_connected_nodes = []
for x in first_degree_connected_nodes:
second_degree_connected_nodes+=list(fb.neighbors(x))
second_degree_connected_nodes.remove(3437)
second_degree_connected_nodes = list(set(second_degree_connected_nodes))
subgraph_3437 =
nx.subgraph(fb,first_degree_connected_nodes+second_degree_connected_nodes)
pos = nx.spring_layout(subgraph_3437)
node_color = ['yellow' if v == 3437 else 'red' for v in subgraph_3437]
node_size = [1000 if v == 3437 else 35 for v in subgraph_3437]
plt.style.use('fivethirtyeight')
plt.rcParams['figure.figsize'] = (20, 15)
plt.axis('off')
nx.draw_networkx(subgraph_3437, pos, with_labels = False,
node_color=node_color, node_size=node_size )
plt.show()
5. 中心性尺度
機械学習モデルの機能として使用できる中心性の尺度は多数あります。そのうち2つを説明します。ここで他の尺度を参照できます。
媒介中心性(Betweenness Centrality): 最も多くの友人をもつユーザだけが重要なのではなく、ユーザーがさまざまな地域からコンテンツを表示できるように、ある地域を別の地域に接続するユーザーも重要です。媒介中心性は、特定のノードが他の2つのノード間で選択された最短のパスに入ってくる回数を定量化します。
次数中心性(Degree Centrality):単純にノードの接続数です。
用途
中心性尺度は、あらゆる機械学習モデルの機能として使用できます。
コード
次はサブグラフの媒介中心性を見つけるためのコードです。
pos = nx.spring_layout(subgraph_3437)
betweennessCentrality = nx.betweenness_centrality(subgraph_3437,
normalized=True, endpoints=True)
node_size = [v * 10000 for v in betweennessCentrality.values()]
plt.figure(figsize=(20,20))
nx.draw_networkx(subgraph_3437, pos=pos, with_labels=False,
node_size=node_size )
plt.axis('off')
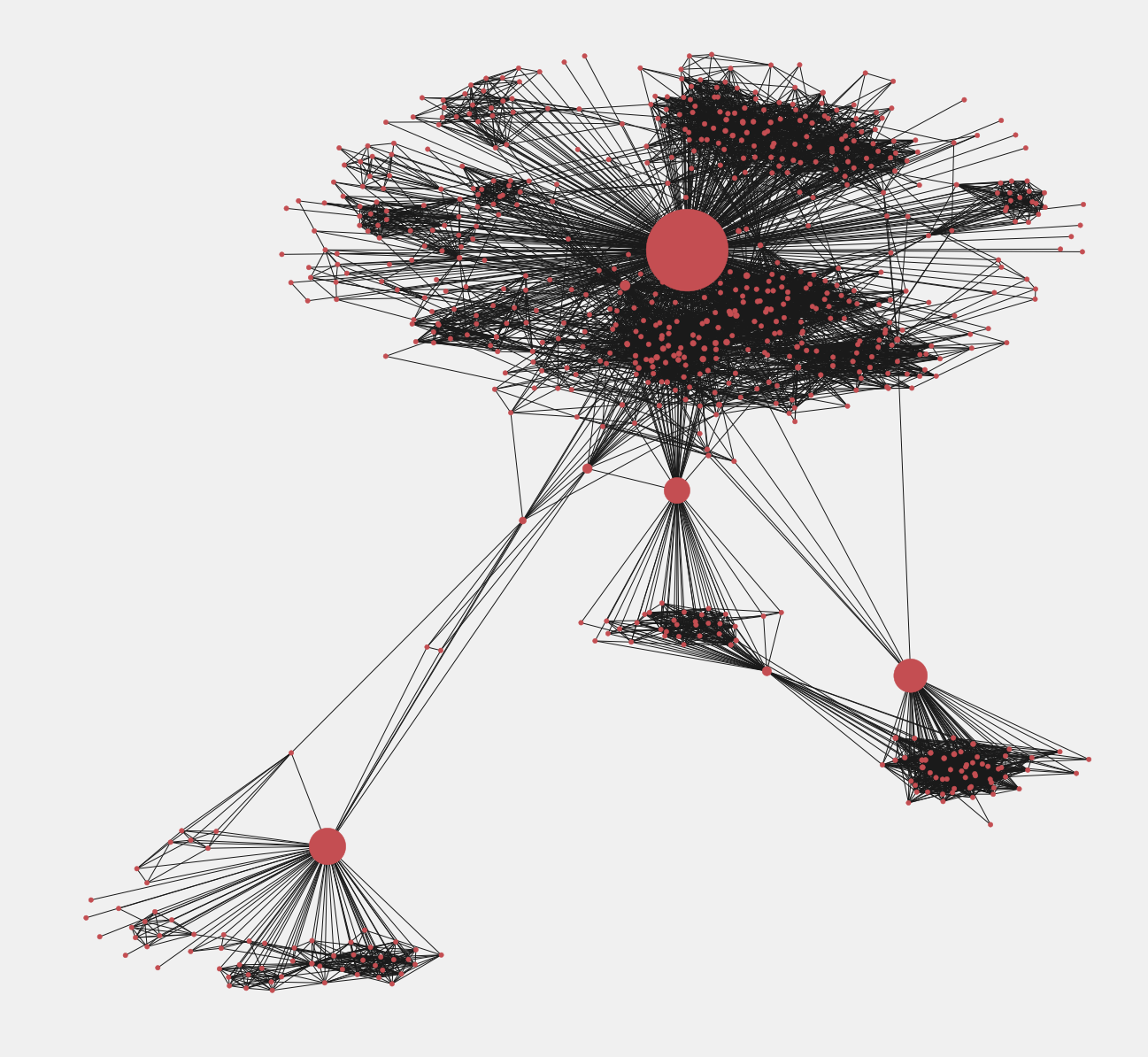
ノード間の中心性の値で大きさが決まったノードを確認できます。それらは情報の伝達者と考えることができます。中心性の値が大きいノードで分割すると、複数のグラフに分割できます。
結論
この記事では、私たちの生活を変えた最も影響力のあるグラフアルゴリズムについて説明しました。
大量のソーシャルデータが出現したことで、ネットワーク分析はモデルの改善と価値の創出に大いに役立つ可能性があります。
そして、もう少し世の中が理解できます。
多くのグラフアルゴリズムがありますが、本記事で紹介したものは私が最も気に入っているアルゴリズムです。必要に応じて、アルゴリズムを詳細に調べてください。この記事は、より知識を広めることを目的としています。
お気に入りのアルゴリズムが他にあれば著者に教えてください。
こちらにKaggleカーネルの全てのコードがあります。
この記事で紹介したグラフアルゴリズムがもっと知りたければ、CourseraでUCSANDiegoが提供しているビッグデータのグラフ分析コースでグラフ理論の基礎を学ぶことを強くお勧めします。
原著者からのメッセージ
読んでくれてありがとうございます。
今後も初心者向けの投稿を書く予定です。
Mediumでフォローアップするか、ブログをサブスクライブして、通知を受けてください。
いつもでも、フィードバックと建設的な批判を歓迎しています。
Twitterの @mlwhizアカウントに連絡してください。
翻訳協力
Author: Rahul Agarwal
Thank you for letting us share your knowledge!
記事選定: yokomichi
翻訳/技術監査: @aoharu / @nyorochan
Markdown化: @ricky