【Unity】18 種類の曲線アルゴリズムを使用できるユーティリティ「UnityCurveUtils」を GitHub に公開しました

備考

この投稿は自分のブログの記事の転載になります
http://baba-s.hatenablog.com/entry/2018/02/22/090000

はじめに

https://github.com/baba-s/unity-curve-utils
「UnityCurveUtils」は 18 種類の曲線アルゴリズムを使用できるユーティリティです

開発環境

• Unity 2017.3.0f3

導入方法

1. 下記のページにアクセスして「UnityCurveUtils.unitypackage」をダウンロードします
   https://github.com/baba-s/unity-curve-utils/blob/master/UnityCurveUtils.unitypackage?raw=true
2. ダウンロードした「UnityCurveUtils.unitypackage」を Unity プロジェクトにインポートします

サンプルシーン

「Example」フォルダ内に、各曲線アルゴリズムの使用例が格納されています

曲線アルゴリズム一覧

B-スプライン曲線

var point = UnityCurveUtils.B_SplineCurve( x1, y1, x2, y2, x3, y3, t );

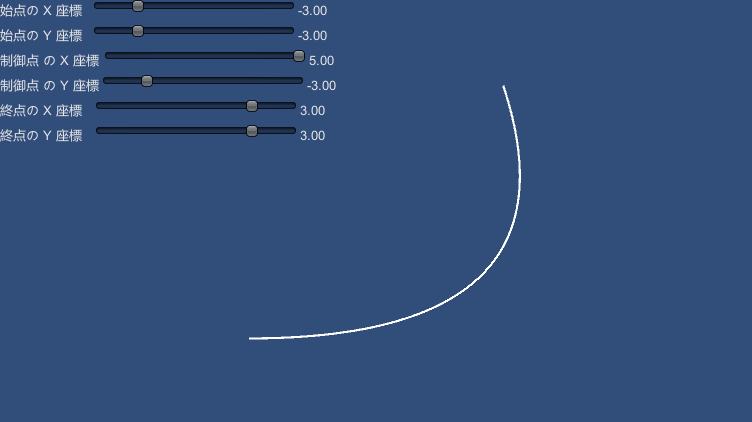
ベジェ曲線

var point = UnityCurveUtils.BezierCurve( x1, y1, x2, y2, x3, y3, x4, y4, t );

双曲螺旋

var point = UnityCurveUtils.HyperbolicSpiral( a, c theta );

アーネシの曲線

var point = UnityCurveUtils.WitchOfAgnesi( a, theta );

デカルトの正葉線

var point = UnityCurveUtils.FoliumOfDescartes( a, theta );

楕円

var point = UnityCurveUtils.Ellipse( a, b, theta );

双曲線

var point = UnityCurveUtils.Hyperbola( a, b, theta );

インボリュート曲線

var point = UnityCurveUtils.InvoluteOfCircle( a, theta );

ストロフォイド

var point = UnityCurveUtils.Strophoid( a, theta );

コンコイド

var point = UnityCurveUtils.Conchoid( a, l, theta );

シッソイド

var point = UnityCurveUtils.Cissoid( a, theta );

リサジュー曲線

var point = UnityCurveUtils.LissajousCurve( A, B, a, b, delta, theta );

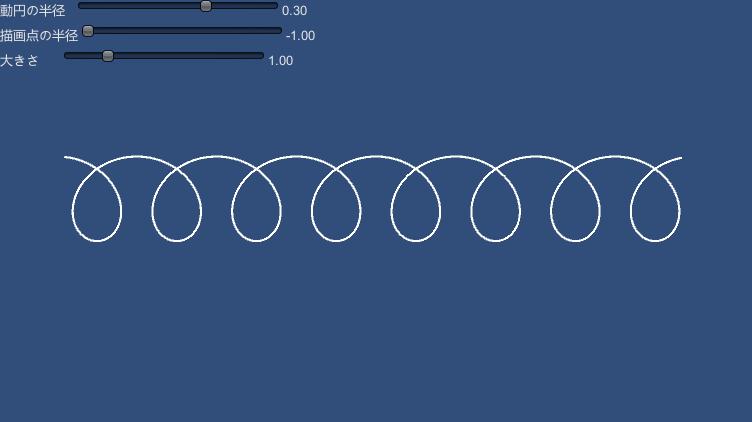
トロコイド

var point = UnityCurveUtils.Trochoid( rm, theta, rd );

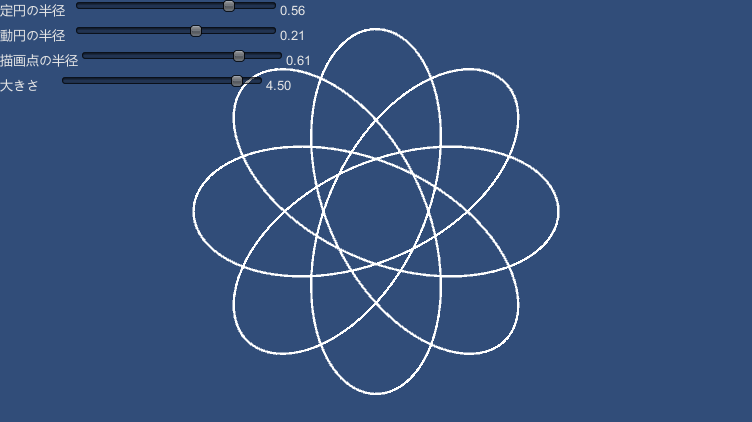
外トロコイド

var point = UnityCurveUtils.Epitrocoid( rc, rm, theta, rd );

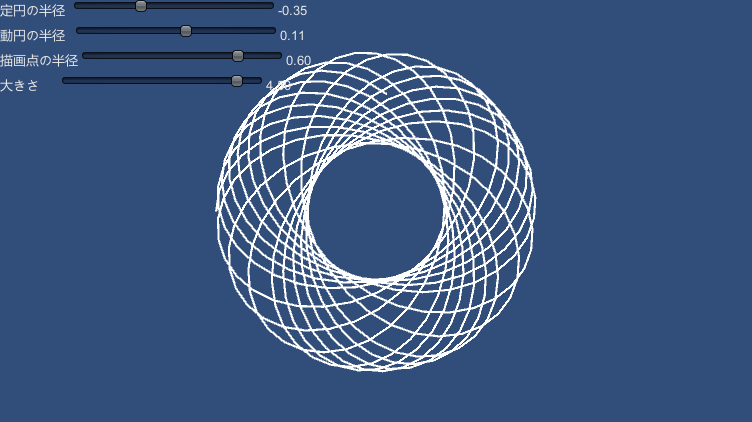
内トロコイド

var point = UnityCurveUtils.Hypetrocoid( rc, rm, theta, rd );

サイクロイド

var point = UnityCurveUtils.Cycloid( rm, theta );

外サイクロイド

var point = UnityCurveUtils.Epicycloid( rm, rd, theta );

内サイクロイド

var point = UnityCurveUtils.Hypocycloid( rm, rd, theta );