はじめに
この記事は MicroAd Advent Calendar 2018 25日目の記事です.
[77, 101, 114, 114, 121, 67, 104, 114, 105, 115, 116, 109, 97, 115]
なおこれはグレイコードではありません.
ゴール
なし
当初は、前回(ScalaのVectorの構造)の続きを書く予定でした.
しかも 12月25日、クリスマス. 木構造の話をするに適した日なのですが🎄🎄🎄🎄🎄🎄
よりみちわきみち. 息抜き. 小ネタ
あと、真摯で真剣なグレイコードの使い道を真摯で真剣に語ることはしません. 今の所できません.
今回使う言語は python です.
グレイコード
英表記は Gray Code で、灰色ではなく、提唱した人の名前からちなんだものだそうです.
意味合いが現れる別の名は Reflected Binary Code です.
wikipedia 引用です.
数値の符号化法のひとつで、
前後に隣接する符号間のハミング距離が必ず1であるというƒ特性を持つ
さらにハミング距離に関しては
ある文字列を別の文字列に変形する際に必要な置換回数を計測したもの
言い換えると、任意の符号(ビット列や文字列)と前後する符号の間に、異なるビットがたったひとつになる並べ方になるでしょうか.
例
2bit の例だと 00 01 11 10 です.
インデックスは左から1と数えて1番目、2番目とすると、
00 と 01 の間異なるビットは1番目のみ
01 と 11 の間異なるビットは1番目のみ
11 と 10 の間異なるビットは2番目のみ
です.
Reflected の異名について
さきほどの 2bit の例で半分切ってみましょう.
00 01 | 11 10
最下位ビットだけとってみると 0 1 | 1 0 と左半分と右半分で対称となっています.
3bit の例でも半分切ってみましょう.
000 001 011 010 | 110 111 101 100
最下位ビットが 0 1 1 0 | 0 1 1 0
そのすぐ上(真ん中)のビットが 0 0 1 1 | 1 1 0 0
と、最上位ビット以外が左半分と右半分で反転コピー(reflected)されます.
最上位ビットに関しては、左半分がすべて0、右半分がすべて1です.
うれしいこと
参照元 👀
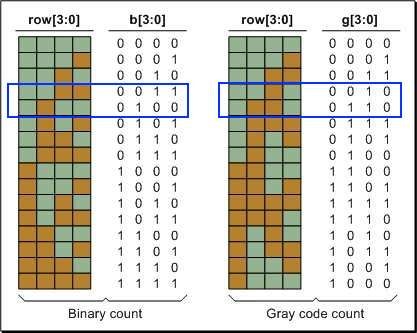
状態の移動をビットで表した図です. ある状態から次の状態へ移行することを考えます.
まず、一般的なバイナリ (0, 1, 2, 3, 4 ... の順をそのまま二進数にした 0000, 0001, 0010, 0011, 100 ..)で並べるケースを考えます.
たとえば 0011 から 0100 に状態を変える際、0011 から三つのビットを同時に変えないと次の 0100 に移行できません.
一方、グレイコードで並べるケースでは、0010 から 0110 への移行が上記の状況に該当しますが、同時に複数のビットを変えず、一つだけ変換することで済みます.
へぇ...そうなんだ.
もくもく
n bit が与えられたときに、n bit グレイコードのリストを生成する会
ビット演算
シンプルな作り方だと、ビット演算することで妥当な次のビットに変換し続ける方法でしょうか.
def gray_code(n):
for k in range(2 ** n):
yield k ^ (k >> 1)
n=3
[0, 1, 3, 2, 6, 7, 5, 4]
- 総ビット数を決める.
'0'と'1'を用いて桁を作るので、
全部で2^n 個生成されます.
- 任意の値を
kとしましょう.kの最下位ビットを捨てる. つまり、右に 1 シフトさせます.
見栄えのためにフォーマット適用
# yield k ^ (k >> 1)
yield f'{k ^ (k >> 1):0{n}b}'
n=3
['000', '001', '011', '010', '110', '111', '101', '100']
再帰
↑ で十分ですが、せっかくなので reflected な性質を利用したものです.
ちょっと素直すぎる方法.
-
n はビットなので、再帰が終わるパターン は 1 bitのとき.
0, 1しか並べようがないです. -
再帰パターンは、一つ前のビットのグレイコードを探すこと.
左半分と、各要素の最上位ビット以外のビットを反転した要素の集まり-右半分-を生成して(最上位ビットに左右それぞれ0と1をくっつけつつ)合体する作業です.
def gray_code(n):
if n == 1:
return [0, 1]
prev = gray_code(n - 1)
return [f'0{k}' for k in prev] + [f'1{k}' for k in reversed(prev)]
だがしかし
フォーマットで(数字を文字列化して)文字をくっつけていくよりは、できれば、数字は数字で扱いたいです.
結局ビット演算
桁(ビット)を扱うときは、シフト演算がシンプルかなと思います.
def gray_code(n):
if n == 1:
return [0, 1]
codes = gray_code(n - 1)
for k in reversed(codes):
codes.append((1 << (n - 1)) + k)
return codes
- 左半分の要素を反転コピー(最上位ビット=
n以外のもの=n-1)して右半分の要素kを生成 - 右半分の最上位ビットは
1なので、1 をn-1ビット左にシフトして最上位ビットを作って、kを足し要素を完成する
の繰り返しで生成していきます.
蛇足で、シフト演算は評価順位が低いのでよしなに括弧で囲んでいます.
数字のまま扱い、特に変換工程も入れてないので、10進数表記で返ってきます.
おわりまして
締めの記事になってしまったので、締めの挨拶をさせていただきます.
冒頭で述べましたが、すてきな [67, 104, 114, 105, 115, 116, 109, 97, 115] をお過ごしください.
そして [72, 97, 112, 112, 121, 78, 101, 119, 89, 101, 97, 114] です.
なおこれらもグレイコードではありません.