初投稿です。
ネット上にMTシステムの情報を充実したいと思い、本記事を執筆しました。この記事をきっかけに、多くの方にMTシステムを活用して頂ければ幸いです。この概要編では、MTシステムを知らない読者を想定して、MTシステムの内容と計算方法について紹介します。
前提知識
基本統計量の知識
線形代数の初歩な知識
判別分析もしくは線形回帰分析の分析経験(※知らなくても構いません)
目次
1.MTシステムの全体像
2.MT法
2-1.MT法の概要
2-2.MT法の考え方
2-3.MT法の計算方法
3.T法
3-1.T法の概要
3-2.T法の考え方
3-3.T法の計算方法
1.MTシステムの全体像
MTシステムを一言で説明すると、
「マハラノビス・タグチ・システムの略であり、品質工学の創始者である田口玄一が考案したパターン認識手法の総称である」
と言えます。
さすがにこれだけでは、聞きなれない用語が多く、分かりにくいと思うので、一つずつ説明していきます。
最初に、田口氏の紹介をします。田口玄一(1924年~2012年)は、統計学者で、戦後の日本企業に実験計画法による品質管理を指導してものづくりに大きく貢献しました。1960年には工業製品の品質管理に貢献した者へ送られるデミング賞を日本人で3人目に受賞し、また1997年に米国自動車殿堂に入っております。田口氏には多くの著書がありますが、丸善から出版されている書籍「実験計画法(上、下の2巻)」は、実験計画法を学ぶ者にとってはバイブル本でもあります。その田口氏が考案した品質工学(Quality Engineering)とは、SN比と呼ばれる尺度を使って、ロバスト設計を目指す技術開発手法のことです。アメリカではタグチメソッド(Taguchi Method)とも呼ばれてます。2022年現在、トヨタ自動車、富士ゼロックス、マツダ、リコーなどの製造業の分野を中心に品質工学は導入されています。その品質工学には、大きく分けて3つの分野があります。
・パラメータ設計
・オンラインの品質工学
・MTシステム
パラメータ設計、オンラインの品質工学ともに興味深い内容ですが、MTシステムを理解するのに、これらの知識は必要ありませんので安心してください。
最後にパターン認識ですが、これは膨大なデータからある規則性に従うデータを識別して取り出す処理を指します。身近なパターン認識として、「顔認証」、「音声認証」、「文字認識」などがあります。
MTシステムは、パターン認識の目的(判別もしくは回帰)に応じて適用する手法が異なります。複数の手法が存在するには、MTシステムの歴史を紐解くと分かりやすいです。1980年代に田口氏は、インドの統計学者であるマハラノビス(1893~1972)博士が命名したマハラノビスの距離をパターン認識に応用して、判別を目的としたMT法(Mahalanobis Taguchi method)を考案しました。その後、東京逓信病院の兼高が、健康診断の結果から健康人と不健康人の判別にMT法を適用しました。MT法は他の事例にも適用され成果を挙げましたが、解決出来ない技術的課題が登場します。それに対して田口氏がMT法の改良手法を考案しました。このようにMTシステムは、
事例検証⇒技術的課題が発生⇒田口氏が新しい手法を考案⇒事例検証⇒技術的課題が発生⇒田口氏が新しい手法を考案するというサイクルにより、進化し続けてきました。この進化の過程で多くの手法が考案されたのです。今日では、それらの総称してMTシステムと呼んでいるのです。
この記事では、MTシステムの原点であるMT法とT法を紹介します。これらは、MTシステムで主流となっている手法です。
T法の正確な表記は、T法(1)ですが、この記事ではT法とします。
用語の説明
この記事で出てくる用語の意味を表1にまとめました。品質工学独自の用語もありますので、ご確認下さい。
表1
| 用語 | 意味 |
|---|---|
| 特徴項目 | データの特徴・特性を定量的に表した数値。特徴量と同義 |
| 真値 | 測定済みで値が判明している目的変数 |
| 学習データ | モデル作成用のデータ |
| 単位空間データ | パターンの基準となるデータ |
| 評価対象サンプル | モデル評価用のサンプル |
2.MT法
2-1 MT法の概要
MT法は、判別問題に対して適用できる分析手法です。例えば、「製品検査で良品と不良品を判別する」、「生産ラインをモニタリングして、故障検知をする」など、異常検知の分野で活用されることが多いです。MT法は判別の対象となるデータ群(これを単位空間と呼びます)を基準点にして、評価対象サンプルとのマハラノビスの距離(Mahalanobis Distance)を計算します。そして設定した閾値から評価対象サンプルが単位空間に属するか属さないかを判定します。

上記の図では、サンプル$A$のマハラノビスの距離$D_{A}$は、閾値$D_{th}$を超えているので、単位空間とは違うサンプルであると判定します。一方、サンプル$B$のマハラノビスの距離$D_{B}$は、閾値$D_{th}$を下回っているので単位空間に属するサンプルであると判定します。多変量解析の判別分析との違いですが、判別分析は予めデータを2群もしくは3群以上に分けて、評価対象サンプルに対して、それぞれの群からのマハラノビスの距離を計算し、距離が近い群にサンプルを分類します。MT法との違いは、定義する群の数となります。
単位空間の作成に必要なデータ構造を示します。ただし、$n$(サンプル数)>$k$(特徴項目数)とします。これは、単位空間の計算過程で逆行列を求めるからです。
x=
\begin{bmatrix}
x_{11} & \cdots & x_{1j} & \cdots & x_{1k}\\
\vdots & \ddots & & & \vdots \\
x_{i1} & & x_{ij} & & x_{ik} \\
\vdots & & & \ddots & \vdots \\
x_{n1} & \cdots & x_{nj} & \cdots & x_{nk}
\end{bmatrix}
MT法は、このデータから単位空間を作成し、評価対象サンプルと単位空間との「離れ具合」を、マハラノビスの距離で測ります。マハラノビスの距離$D$は次の式で計算します。
D=\sqrt{\frac{1}{k}X^{t}R^{-1}X}
$X$は、$x$を基準化した行列で、$R^{-1}$は、$X$の相関行列の逆行列です。この距離$D$は、特徴項目間の相関構造を考慮した距離で、馴染みのあるユーグリッド距離と同じくスカラー値です。
2-2 MT法の考え方
MT法は、単位空間という1つの群からの距離を考え、評価対象サンプルの判別を行います。単位空間に相応しいデータとは、均一なデータ群であるとされています。これは、異常検知という考え方からすると、納得できると思います。MT法が活躍する場面は、製品の検査や工程管理などが多いのですが、これらは「正常(良品)もしくは異常(不良)」の判別を行うものです。具体例で考えてみましょう。製品検査で良品と不良品を判別する際に、良品のサンプルは大量にありますので、群を作りやすいです。つまり良品はサンプル同士が似ているため、均一なデータだと言えます。一方、不良品に関しては、サンプル数が少なかったり、そもそもサンプルがないこともあります。(不良率が大きい場合は、MT法を使う前に工程の対策に取り組むべきです。)また不良の発生モードも様々で群を分けるのは一般的に難しいです。以上のことから判別分析を製品検査に適用すると、データ数が少ない、群を定義しづらいなどの問題があるため解析が難しいです。それに対してMT法は、良品を基準とする単位空間だけを考えて、判別を行います。
単位空間の考え方について、初期のMT法の適用事例でもある兼高による「MT法による健康診断」を参考に深掘りしたいと思います。この事例は、健康診断の検査項目(血液検査や尿検査、性別など)から疾患(論文では肝硬変)の有無をMT法で判別するというものです。疾患あの有無の判断ですが、検査項目間に相関があるため、一つの項目値だけで判断することが出来ません。そこで、相関を考慮出来るマハラノビスの距離を総合指標として、提案しました。単位空間は、病気がない健康な正常人(200人)です。この単位空間は、検査値だけでなく、専門知識を有する判定員が最終的に決定しています。この事例のポイントは、
・単位空間は、均一なデータ群である。
・人が最終的に判定して単位空間データに入れている。
単位空間を定義する上で最も大事なことは、専門家の判断を取り入れることです。
単位空間は必ずしも理想的な状態を指すわけではありません。例えば、先ほどの正常人を健康的な若者だけで作成すると、単位空間は厳しいものになり、正常人と疾患がある人との判別が出来ない恐れがあります。
閾値の決め方には、いくつか方法があるのでご紹介します。
方法1 χ二乗分布を利用する。
MT法は、各特徴項目が多変量正規分布に従うと仮定する場合、MD値は自由度$k$の$\chi$二乗分布に従います。この性質を利用すれば、閾値を統計的に決めることが出来ます。
方法2 評価対象サンプルのMD値から決める。
異常サンプルを複数用意し、マハラノビスの距離を計算します。異常の程度が軽微な(例:社内出荷規格を満たさない)サンプルのMD値を閾値に設定します。筆者としてはこの方法をお勧めします。
2-3. MT法の計算方法
この節では、単位空間の作成方法と評価対象サンプルの計算方法を解説します。
単位空間の作成
手順1-1 単位空間データの平均値と標準偏差を計算する
手順1-2 単位空間データの基準化を行う
手順1-3 相関行列を計算する
手順1-4 逆行列を計算する
手順1-5 単位空間データのMDを計算する
評価対象サンプルの計算
手順2-1 評価対象サンプルの基準化を行う
手順2-2 MDを計算する
それでは、手順に沿って解説します。最初にやることは、学習データから単位空間を作成することです。
手順1-1 単位空間データの平均値と標準偏差を計算する
各特徴項目で平均値と標準偏差を計算します。標準偏差が$0$となった項目は、基準化が出来ないので除外します。なお、単位空間のサンプル数$n$は、目安として特徴項目数の$3\sim4$倍が良いとされています。
\begin{eqnarray}
\bar{x}_{j}&=&\frac{x_{1j}+x_{2j}+\dots+x_{nj}}{n}\\
\sigma_{j}&=&\sqrt{\frac{1}{n}\sum_{i=1}^n(x_{ij}-\bar{x}_{j})^2}\\
\end{eqnarray}
平均値と標準偏差を計算した後の単位空間データを表$2.1$に示します。
表$2.1$
| No | $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{k}$ |
|---|---|---|---|---|
| $1$ | $x_{11}$ | $x_{12}$ | $\cdots$ | $x_{1k}$ |
| $2$ | $x_{21}$ | $x_{22}$ | $\cdots$ | $x_{2k}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| $n$ | $x_{n1}$ | $x_{n2}$ | $\cdots$ | $x_{nk}$ |
| $\bar{x}$ | $\bar{x}_{1}$ | $\bar{x}_{2}$ | $\cdots$ | $\bar{x}_{k}$ |
| $\sigma$ | $\sigma_{1}$ | $\sigma_{2}$ | $\cdots$ | $\sigma_{k}$ |
手順1-2 単位空間データの基準化を行う
手順1-1で求めた平均値と標準偏差を使って、基準化を行います。
\begin{eqnarray}
X_{ij}&=&\frac{x_{ij}-\bar{x}_{j}}{\sigma_{j}}\hspace{2mm}(i=1,2,\cdots,n \hspace{2mm}j=1,2,\cdots,k)\\
\end{eqnarray}
基準化後の単位空間データの表$2.2$を示します。基準化後の平均値は$0$、標準偏差は$1$になります。
表$2.2$
| No | $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{k}$ |
|---|---|---|---|---|
| 1 | $X_{11}$ | $X_{12}$ | $\cdots$ | $X_{1k}$ |
| 2 | $X_{21}$ | $X_{22}$ | $\cdots$ | $X_{2k}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| $n$ | $X_{n1}$ | $X_{n2}$ | $\cdots$ | $X_{nk}$ |
| $\bar{x}$ | $0$ | $0$ | $\cdots$ | $0$ |
| $\sigma$ | $1$ | $1$ | $\cdots$ | $1$ |
手順1-3 相関行列を計算する
基準化後の単位空間データを用いて、特徴項目間の相関係数を計算します。
r_{pq}=r_{qp}=\frac{\sum_{i=1}^n(X_{ip}X_{iq})}{\sum_{i=1}^nX_{ip}^2\sum_{i=1}^nX_{iq}^2}\\
計算した相関係数から相関行列を作ります。相関係数が$1$もしくは$-1$、またはそれらに非常に近い値(例えば$0.999$や$-0.999$など)を取る項目の組み合わせは、多重共線性が発生していますので、どちらかの項目を削除します。なお行列の対角成分は、同一の特徴項目なので、相関係数は必ず1になります。
R=
\begin{pmatrix}
1 & \cdots & r_{1i} & \cdots & r_{1k}\\
\vdots & \ddots & & & \vdots \\
r_{i1} & & 1 & & r_{ik} \\
\vdots & & & \ddots & \vdots \\
r_{k1} & \cdots & r_{ki} & \cdots & 1
\end{pmatrix}
手順1-4 逆行列を計算する
相関行列の逆行列を計算します。逆行列は、RやPython等のソフトウェアを用いれば簡単に求まります。これらのプログラミング経験がない方は、Excelの関数を使えば、計算が出来ます。
R^{-1}=
\begin{pmatrix}
a_{11} & \cdots & a_{1i} & \cdots & a_{1k}\\
\vdots & \ddots & & & \vdots \\
a_{i1} & & a_{ii} & & a_{ik} \\
\vdots & & & \ddots & \vdots \\
a_{k1} & \cdots & a_{ki} & \cdots & a_{kk}
\end{pmatrix}
手順1-5 単位空間データのMDを計算する
基準化後の単位空間データと相関行列の逆行列を用いて、$MD$を計算します。
D_{i}=\sqrt{\frac{1}{k}(X_{i1},X_{i2},\cdots,X_{ik})
\begin{pmatrix}
a_{11} & \cdots & a_{1i} & \cdots & a_{1k}\\
\vdots & \ddots & & & \vdots \\
a_{i1} & & a_{ii} & & a_{ik} \\
\vdots & & & \ddots & \vdots \\
a_{k1} & \cdots & a_{ki} & \cdots & a_{kk}
\end{pmatrix}
\begin{pmatrix}
X_{i1}\\
X_{i2}\\
\vdots\\
X_{ik}\\
\end{pmatrix}}\\
=\sqrt{\frac{1}{k}\textbf{X}^t_{i}R^{-1}\textbf{X}_{i}}
単位空間データの距離$D$の二乗の平均値は、$1$になります。
\frac{1}{n}{\sum_{j=1}^nD^2_{j}}=1
$1$にならない場合は、特徴項目間に多重共線性が発生しているので、特徴項目の見直しが必要です。
次に評価対象サンプルのマハラノビスの距離($D$)を計算します。
手順2-1 評価対象サンプルの基準化を行う
単位空間データの平均値と標準偏差を用いて、評価対象サンプルの基準化を行います。
\begin{eqnarray}
X^{\prime}_{j}&=&\frac{x^{\prime}_{j}-\bar{x}_{j}}{\sigma_{j}}\hspace{2mm}(\hspace{2mm}j=1,2,\cdots,k)\\
\end{eqnarray}
基準化後の評価対象サンプルは、
| $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{k}$ | |
|---|---|---|---|---|
| $test$ | $X^{\prime}_{1}$ | $X^{\prime}_{2}$ | $\cdots$ | $X^{\prime}_{k}$ |
となります。
手順2-2 MDを計算する
相関行列$R^{-1}$を用いて、マハラノビスの距離を計算します。
D=\sqrt{\frac{1}{k}(X^{\prime}_{1},X^{\prime}_{2},\cdots,X^{\prime}_{k})
\begin{pmatrix}
a_{11} & \cdots & a_{1i} & \cdots & a_{1k}\\
\vdots & \ddots & & & \vdots \\
a_{i1} & & a_{ii} & & a_{ik} \\
\vdots & & & \ddots & \vdots \\
a_{k1} & \cdots & a_{ki} & \cdots & a_{kk}
\end{pmatrix}
\begin{pmatrix}
X^{\prime}_{1}\\
X^{\prime}_{2}\\
\vdots\\
X^{\prime}_{k}\\
\end{pmatrix}}\\
=\sqrt{\frac{1}{k}\textbf{X}^{\prime{t}}R^{-1}\textbf{X}^{\prime}}
マハラノビスの距離$D$が閾値$D_{th}$を超えたら、異常と判定します。
3.T法
3-1. T法の概要
T法(Taguchi-method)とは、回帰問題に対して適用出来る手法です。例えば、気象データから売上を予測する、年収や家族構成などから住宅価格を推定するなどです。対象となるデータの構造は、重回帰分析と同じで、推定対象の目的変数$M$とそれを関係のある特徴項目$x$です。ちなみにサンプル数$n$は、最低3個以上あれば解析が出来ます。また特徴項目$k$の数に制約はありません。
x=
\begin{bmatrix}
x_{11} & \cdots & x_{1j} & \cdots & x_{1k}\\
\vdots & \ddots & & & \vdots \\
x_{i1} & & x_{ij} & & x_{ik} \\
\vdots & & & \ddots & \vdots \\
x_{n1} & \cdots & x_{nj} & \cdots & x_{nk}
\end{bmatrix}
M=
\begin{bmatrix}
M_{1}\\
M_{2}\\
\vdots\\
M_{n}\\
\end{bmatrix}\\
目的変数$M$は連続値とします。学習データから二つのパラメータ($\eta$と$\beta$)を算出し、総合推定式と呼ばれる回帰式を作成して、目的変数$M$の推定が出来ます。その総合推定式は、次の式で表します。
M^\ast_{i}=\frac{\eta_1\frac{X_{i1}}{\beta_1}+\eta_2\frac{X_{i2}}{\beta_2}+\cdots+\eta_k\frac{X_{ik}}{\beta_k}}{\eta_1+\eta_2+\cdots+\eta_k}\quad(i=1,2,\cdots,n)
T法では、総合推定式で求めた推定値$M^\ast$を総合推定値と言います。$X$は、$x$を各列の平均値で引いた行列(中心化行列)です。パラメータの意味は、後ほど説明します。さて、総合推定式は複雑な構造の式に見えますが、次のように式変形を行うと
\begin{align}
\frac{\eta_1\frac{X_{i1}}{\beta_1}+\eta_2\frac{X_{i2}}{\beta_2}+\cdots+\eta_k\frac{X_{ik}}{\beta_k}}{\eta_1+\eta_2+\cdots+\eta_k}&=\frac{1}{\sum_{j=1}^k\eta_{j}}\{\frac{\eta_1}{\beta_1}X_{i1}+\frac{\eta_2}{\beta_2}X_{i2}+\cdots+\frac{\eta_k}{\beta_k}X_{ik}\}\\&\frac{1}{\sum_{j=1}^k\eta_{j}}\frac{\eta_{i}}{\beta_{i}}=a_{i}と置く\\
&=a_{1}X_{i1}+a_{2}X_{i2}+\cdots+a_{k}X_{ik}
\end{align}
となり、回帰係数$a$と特徴項目$X$の組み合わせで表現することが出来ます。これは、見慣れた重回帰式と同じ形になっていますので、T法が重回帰分析と同様に、複数の特徴項目から目的変数を推定する手法だと分かります。
3-2. T法の考え方
この節では、T法の考え方について解説します。T法は、各特徴項目$X_{j}$で目的変数$M$との単回帰を行い、二つのパラメータ($\eta$と$\beta$)を算出して、総合推定式を作成し、総合推定値$M^\prime_{i}$を求めます。$\beta$は比例定数と呼ばれ、特徴項目と目的変数間の回帰式の傾きを表しています。$\eta$は、SN比と呼ばれ、回帰直線からの各サンプルのバラつきの逆数を表しています。$\eta$の値は、その特徴項目と目的変数間の線形性の強さを意味しています。
T法は、数理的には単回帰の重ね合わせを計算しているですが、線形回帰の単回帰分析と違いがあります。通常の単回帰分析は、特徴項目と目的変数の間に$M=\beta_{1} x+\beta_{0}$という線形関係を仮定して、最小二乗法により回帰係数$\beta_{1},\beta_{0}$を求めます。T法も同様に特徴項目と目的変数の間に線形関係を仮定するのですが、その式は、$x=\beta_{1} M$という式で表します(定数項がないことに注意します)。この違いを図で表現すると、
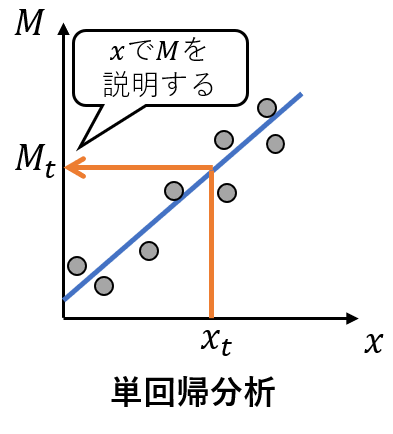
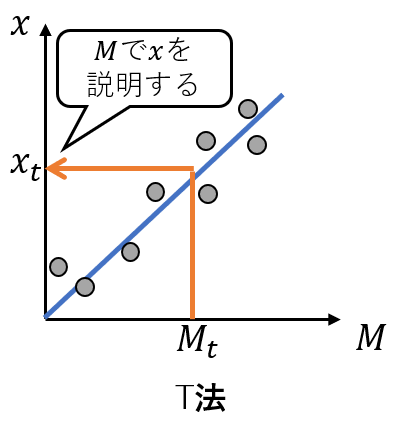
となります。T法は、目的変数から各特徴項目との傾き$\beta$を求め$X_{j}/\beta_{j}$で$M_{i}$の推定つまり逆回帰を行っているのです。
これは、総合推定式を式変形することで分かります。
\begin{align}
\frac{1}{\sum_{j=1}^k\eta_{j}}\{\frac{\eta_1}{\beta_1}X_{i1}+\frac{\eta_2}{\beta_2}X_{i2}+\cdots+\frac{\eta_k}{\beta_k}X_{ik}\}\\\frac{\eta_{i}}{\sum_{j=1}^k\eta_{j}}=b_{i},\frac{X_{i1}}{\beta_{i}}=M_{i1}と置くと\\
=b_{1}M_{i1}+b_{2}M_{i2}+\cdots+b_{k}M_{ik}
\end{align}
となり、総合推定式が、各特徴項目を傾き$\beta$で割り求めた推定値$M$に、$b$で重み付けした式であることが分かります。この式変形からT法が$\beta$で$M$を逆推定し、「総合して」推定値を求めていることが分かると思います。
T法の数学的な特徴について、重回帰分析と比較しながら述べます。
1.n(サンプル数)<k(特徴項目数)でも推定式の作成ができる。
重回帰分析は、特徴項目間の相関構造を利用して、回帰式を作成します。一方、T法は、特徴項目間の相関構造を利用しません。これは、次の図に示すように、両手法の背後に想定するモデルが異なるからです。
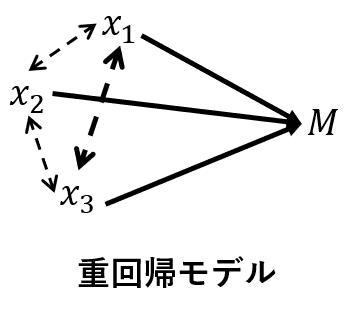
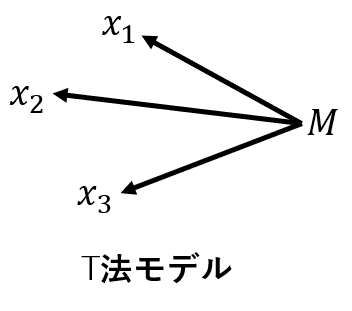
重回帰分析は、$n$(サンプル数)<$k$(特徴項目数)だと、逆行列を求めることが出来ないので、解析が出来ません。
2.多重共線性の有無に関わらず推定式の作成ができる。
重回帰分析は、多重共線性が生じると、行列式の値が不安定になり、信頼性のある結果を得ることが出来ません。
3.四則演算のみで計算ができる。
特徴項目の個数が多くなると、有償のソフトウェアか、PythonやR等のプログラミングが必要になります。(Excelでもデフォルトの分析ツールで解析出来ますが、説明変数の個数に上限があります。)
ここで、注意事項があります。それは、「推定式の作成が可能=予測精度が高い」ということではありません。T法はあくまで、他手法より数学的な制約が少ないだけで、予測精度が優れているわけではないのです。しかし、この制約の少なさが実務の場面では、非常に有利になります。
3-3. T法の計算方法
この節では、総合推定式の作成方法と評価対象サンプルの推定値の計算方法を解説します。
総合推定式の作成方法
手順3-1 学習データの各特徴項目及び真値の平均値を計算する
手順3-2 学習データの校正を行う
手順3-3 比例定数とSN比を各特徴項目で求める
手順3-4 総合推定式を作成して、総合推定値を求める
評価対象サンプルの推定値の求め方
手順4-1 評価対象サンプルの校正を行う
手順4-2 校正後の評価対象サンプルを総合推定式に代入する
それでは、手順に沿って解説します。最初にやることは、学習データから総合推定式を作成します。
手順3-1 学習データの各特徴項目及び真値の平均値を計算する
表$3.1$に示すような学習データを用意します。
表$3.1$
| No | $M$ | $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{k}$ |
|---|---|---|---|---|---|
| $1$ | $M_{1}$ | $x_{11}$ | $x_{12}$ | $\cdots$ | $x_{1k}$ |
| $2$ | $M_{2}$ | $x_{21}$ | $x_{22}$ | $\cdots$ | $x_{2k}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| $n$ | $M_{n}$ | $x_{n1}$ | $x_{n2}$ | $\cdots$ | $x_{nk}$ |
| 次の式に従い、平均値を計算します。 |
\begin{eqnarray}
\bar{x}_{j}&=&\frac{x_{1j}+x_{2j}+\dots+x_{nj}}{n}\quad(j=1,2,\cdots,k)\\
\bar{M}&=&\frac{M_{1}+M_{2}+\dots+M_{n}}{n}\\
\end{eqnarray}
計算後の学習データは表$3.2$になります。
表$3.2$
| $M$ | $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{k}$ | |
|---|---|---|---|---|---|
| $1$ | $M_{1}$ | $x_{11}$ | $x_{12}$ | $\cdots$ | $x_{1k}$ |
| $2$ | $M_{2}$ | $x_{21}$ | $x_{22}$ | $\cdots$ | $x_{2k}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| $n$ | $M_{n}$ | $x_{n1}$ | $x_{n2}$ | $\cdots$ | $x_{nk}$ |
| $Ave$ | $\bar{M}$ | $\bar{x}_{1}$ | $\bar{x}_{2}$ | $\cdots$ | $\bar{x}_{k}$ |
MTシステムをよくご存じの方へ
T法には、学習データから単位空間データを選び、その平均値を求める計算方法があります。参考文献の書籍でもそのやり方を紹介しております。一方、学習データの平均値を求める方法は、早稲田大学の永田らが提案したTa法と呼ばれます。この記事では、後者のTa法を紹介しました。理由は、Ta法は、解析者の恣意性が入ることなく平均値を求められるからです。
手順3-2 学習データの校正を行う
学習データから手順3-1で求めた平均値を引きます。この操作を「校正」と言います。校正を行うことで、切片項なしの単回帰を想定します。
\begin{eqnarray}
X_{ij}&=&x_{ij}-\bar{x}_{j}\quad(i=1,2,\cdots,n\quad j=1,2,\cdots,k)\\
M^{\ast}_{i}&=&M_{i}-\bar{M}\quad(i=1,2,\cdots,n)\\
\end{eqnarray}
校正後の学習データは、表$3.3$のようになります。
表$3.3$
| No | $M$ | $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{k}$ |
|---|---|---|---|---|---|
| $1$ | $M^{\ast}_{1}$ | $X_{11}$ | $X_{12}$ | $\cdots$ | $X_{1k}$ |
| $2$ | $M^{\ast}_{2}$ | $X_{21}$ | $X_{22}$ | $\cdots$ | $X_{2k}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| $n$ | $M^{\ast}_{n}$ | $X_{n1}$ | $X_{n2}$ | $\cdots$ | $X_{nk}$ |
手順3-3 比例定数とSN比を各特徴項目で求める
校正後の学習データから、各特徴項目で比例定数$\beta$とSN比$\eta$を計算します。少し長い計算ですが、Excel等の表計算ソフトウェアを活用すれば、簡単に求まります。
\begin{eqnarray}
r&=&{M_{1}^{\ast}}^2+{M_{2}^{\ast}}^2+\cdots+{M_{i}^{\ast}}^2\\
&=&{\sum_{i=1}^n{M^{\ast}_{i}}^2}\\
\beta_{j}&=&\frac{\sum_{i=1}^nX_{ij}M^{\ast}_{i}}{r}\\
S_{T_{j}}&=&X_{1j}^2+X_{2j}^2+\cdots+X_{ij}^2\\
&=&{\sum_{i=1}^nX_{ij}^2}\\
S_{\beta_{j}}&=&\frac{(\sum_{i=1}^nX_{ij}M^{\ast}_{i})^2}{r}\\
S_{e_{j}}&=&S_{T_{j}}-S_{\beta_{j}}\\
V_{e_{j}}&=&\frac{S_{e_{j}}}{n-1}\\
\eta_{j}&=&\begin{cases}\frac{\frac{1}{r}(S_{\beta_{j}}-V_{e_{j}})}{V_{e_{j}}}\quad(S_{\beta_{j}}>V_{e{j}})\\\hspace{8mm}{0}\hspace{14mm}(S_{\beta_{j}}\leq V_{e{j}})\end{cases}
\end{eqnarray}
この計算を$x_{1}からx_{k}$まで行い、$k$通りの比例定数$\beta$とSN比$\eta$が得られます。
表$3.4$
| $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{k}$ | |
|---|---|---|---|---|
| $\beta$ | $\beta_{1}$ | $\beta_{2}$ | $\cdots$ | $\beta_{k}$ |
| $\eta$ | $\eta_{1}$ | $\eta_{2}$ | $\cdots$ | $\eta_{k}$ |
SN比$\eta$は、値の符号により場合分けをします。SN比が負の値をとる場合、それは誤差分散$V_{e}$が回帰変動$S_{\beta}$より大きいことを意味しますので、その特徴項目のSN比は0と置き換えます。この操作を特徴項目の絞り込みといいます。特徴項目の絞り込みにより、推定に寄与しない特徴項目は自動的に落とされ、総合推定式に含まれません。
手順3-4 総合推定式を作成して、総合推定値を求める
校正後の学習データを比例定数$\beta$で割り、SN比$\eta$で加重平均を取ることで、総合推定値を求めます。総合推定値に手順3-1で求めた$\bar{M}$を足せば、校正前の総合推定値となります。
M^\prime_{i}=\frac{\eta_1\frac{X_{i1}}{\beta_1}+\eta_2\frac{X_{i2}}{\beta_2}+\cdots+\eta_k\frac{X_{ik}}{\beta_k}}{\eta_1+\eta_2+\cdots+\eta_k}+\bar{M}\quad(i=1,2,\cdots,n)
これで学習データの総合推定値を求めることが出来ました。作成した総合推定式の推定精度は、決定係数$R^{2}$やRSSなどの指標を使って評価します。
次に、作成した総合推定式を使って、評価対象サンプルの推定を行います。
手順4-1 評価対象サンプルの校正を行う
手順3-1の平均値を使って評価対象サンプル$x^{\prime}$の校正を行います。
表$3.5$
| $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{k}$ | |
|---|---|---|---|---|
| $test$ | $x^{\prime}_{1}$ | $x^{\prime}_{2}$ | $\cdots$ | $x^{\prime}_{k}$ |
次の式に従い、計算します。
\begin{eqnarray}
X^{\prime}_{j}&=&x^{\prime}_{j}-\bar{x}_{j}\quad(j=1,2,\cdots,k)\\
\end{eqnarray}
校正後の評価対象サンプルは、次の表$3.6$のようになります。
表$3.6$
| $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{k}$ | |
|---|---|---|---|---|
| $test$ | $X^{\prime}_{1}$ | $X^{\prime}_{2}$ | $\cdots$ | $X^{\prime}_{k}$ |
手順4-2 校正後の評価対象サンプルを総合推定式に代入する
校正後の評価対象サンプルを比例定数$\beta$で割り、SN比$\eta$で加重平均を取ることで、総合推定値を求めます。総合推定値に順3-1で求めた$\bar{M}$を足せば、校正前の総合推定値となります。
M^\prime=\frac{\eta_1\frac{X^\prime_{1}}{\beta_1}+\eta_2\frac{X^\prime_{2}}{\beta_2}+\cdots+\eta_k\frac{X^\prime_{k}}{\beta_k}}{\eta_1+\eta_2+\cdots+\eta_k}+\bar{M}
評価対象サンプルの予測精度は、$PE$などを使って評価します。
参考文献
ネット上の記事
SN比$\eta$の導出部分などを参考にさせて頂きました。スタビジさんは、良質な記事がたくさんありますので、ぜひ訪れてみて下さい。
一般書籍
田村希志臣著:「よくわかるMTシステム 品質工学によるパターン認識の新技術」,日本規格協会
MTシステムの入門書です。MTシステムの歴史や計算方法などを分かりやすく説明しています。この記事では取り上げなかった手法の説明もあります。
立林和夫著:「入門タグチメソッド」,日科技連出版社
代表的な品質工学の入門書です。パラメータ設計、オンラインの品質工学、MTシステムが書かれているため、品質工学全体を知りたい人にはお勧めです。
宮川雅巳著:「品質を獲得する技術-タグチメソッドがもたらしたもの-」,日科技連出版社
研究者向けの本です。内容はやや高度ですが、数理的な立場から品質工学の理解が出来ます。
論文
兼高達貳(1997):「マハラノビスの距離を応用した健康診断の判定」,品質工学会誌誌5-2
記事中に取り上げたMT法の初期の適用事例です。
稲生淳紀, 永田靖, 堀田慶介, 森有紗(2012):「タグチのT法およびその改良手法と重回帰分析の性能比較」,日本品質管理学会誌42 265-277
T法と重回帰分析をモンテカルロシミュレーションを使って予測精度の比較を行っています。この記事でも取り上げたT法の改良手法であるTa法が提案されています。