「クラスタリング(Clustering)という言葉を知っている」という程度の方を対象に、クラスタリングとは何か、どこで使えるのかという話から、どんな方法で実現するのかという話までを説明する記事です。
また、本記事は、courseraで提供されているAndrew Ng氏の機械学習講義の内容を参考に、「クラスタリング」に関して説明するものです。
取り上げるアルゴリズムは「K-Means法」のみで、その他のアルゴリズムについて説明は行いませんのでご了承ください。
クラスタリングとは?
概要
「クラスタリング(または、クラスタ分析・クラスタ解析)」とは簡単に言えば、集団を、ある規則・共通項に従って分類・グルーピングする手法です。
データの集合をラベルなどの外的基準なしに分類する手法であり、「教師なし学習」の一種でもあります。
「教師なし学習」とは「教師あり学習」に対して使われる言葉です。
以下の画像は、それぞれの方法で利用するデータのイメージです。

「教師あり学習」とは、あらかじめラベリングされたデータ(=教師データ)を基に学習を行い、ラベリングされていないデータのラベリングを行うことを目的にするもので、学習と分類という二つの段階があります。
対して「教師なし学習」は、ラベリングされていないデータに対して何らかの特徴を見出し、識別するというもので、分類方法の判断自体から行わせるもので、基本的にはアルゴリズムにデータを投げるだけで何かしらの結果を得ることができます。
今回取り上げる**「クラスタリング」は、「教師なし学習」**の一例となります。
利用シーン
「クラスタリング」はその名の通り、集団をクラスタ(=同種の特徴を持つ集団)に分割する、あるいはそういった集団を取り出すことを目的に使用されます。
それは、例えば以下のような場合に適用することができます。
- 顧客情報の分析
- ソーシャルネットワーク上の繋がりのグルーピング
- 服のサイズの決定
顧客の分析やソーシャル上の繋がりに対するクラスタリングは、得られたクラスタの傾向を基に、商品やユーザーをレコメンドするといったことが実現できます。
身近な例としては、某密林で「この商品を買った人はこんな商品も買っています」という言葉を見たことがあるのではないでしょうか。
これもクラスタリングのちょっとした応用で、「ある商品を買った人」というクラスタに属する人に、同じクラスタに属する人が買った商品をレコメンドしているというものです。
※実際にはもっと複雑なことをしていると思いますが…。
種類
クラスタリングアルゴリズムは、大まかに「階層的手法」と「非階層的手法」の二つに分類されます。
両者の特徴を以下にまとめます。
- 階層的手法(下記イメージ)
- N個のデータそれぞれに対して、N個のクラスタを設定し、最も距離の近いクラスタ同士を併合する
- 一つのクラスタになるまで、階層的に併合を繰り返す
- 非階層的手法(後述)
- 直接的に、何らかの手段でK個のクラスタに分割する
- 段階は踏むが、クラスタの数は不変である
階層的手法のアルゴリズムは、主に距離計算手法に違いが見られます。
また、階層的手法は、結果として樹形図を得ることができ、それをもとに分割するクラスタ数を後から決めることができます。
代表的なものとして以下のアルゴリズムがあります(それ以外にもあります)。
- ウォード法
- 最短距離法
- 最長距離法
階層的手法に対して、非階層的手法はあらかじめクラスタ数を決めたうえでクラスタリングを行う手法です。
非階層的手法の代表的なものはK-Means法で、本記事以下で説明します。
K-Means法
基本的な考え方
適当な場所に、分割したいクラスタの数だけ重心を置き、以下の手順を適当な回数繰り返すというのが基本的な流れです。
- 各データを、最も近い重心に関連付ける
- 重心を、その重心に関連付けられたデータの平均地点に移動する
ここで、クラスタの数は、概ねKという文字で示されます。
つまり、このアルゴリズムはK個のクラスタに属する要素それぞれの平均をとるという作業を繰り返すもので、ゆえにK-Means法と呼ばれます。
以下の画像は、この手順を図示したものです。
この作業の繰り返しは、アルゴリズムとして、以下のようにあらわすことができます。
ここで、各文字は以下を表します。
- K : クラスタの数
- μ : 各重心座標
- c : 各xが割り当てられる重心の番号
- x : 各データセットの値
Jは最適化するべき目的関数です。
Jは、重心と各データセットの距離の二乗和の平均をとるもので、単純にこの値が小さいほど、各データセットが適切な重心に割り当てられていることがわかります。
クラスタリングのアルゴリズムにおいて、データを重心に割り振る際には、このJが最少となるように割り当て、また、重心を移動する際にもJが最少となるような位置へ移動させます。
また、このJの変化をトラッキングしておくと、その値が適切に減少していっているかを見ることで、クラスタリングアルゴリズムが正常に実行されているかどうか判断することもできます。
K-Means法のアルゴリズムの説明はここまでです。
後は上記アルゴリズムを、各プログラミング言語に合わせて実装するだけで、分類問題に適用することが可能です。
分割されていない集団への適用
上記例は、ある程度分割されているようにみられる集団に対しての適用例でした。
しかし、クラスタリングを適用できる例は、分割された集団に限りません。
以下の例は明確に分かれていない集団に対して適用してみたものです。

上記の例で、身長と体重という情報を軸に当てはめると、人の体格をプロットしたものと見ることができるでしょう。
その場合、クラスタリング結果は、単純に服のサイズの設定に使用することもできるでしょうし、クラスタの大きさから服の生産数を決める指標として利用することも可能でしょう。
このような例への適用は、珍しいものではありません。
むしろ、人の手で判断しにくいからこそ、こういったアルゴリズムが活用されるのです。
故に、こういった分けにくいデータの分割こそ、クラスタリングが本当に活きる場面といえます。
重心の取り方-ランダム初期化
ここまで、K-Means法の基本的な考え方や適用方法を示しました。しかし、例として挙げた画像はあくまで理想的に遷移した場合の例になります。
しかし、実際には以下のような現実に直面することがままあります。
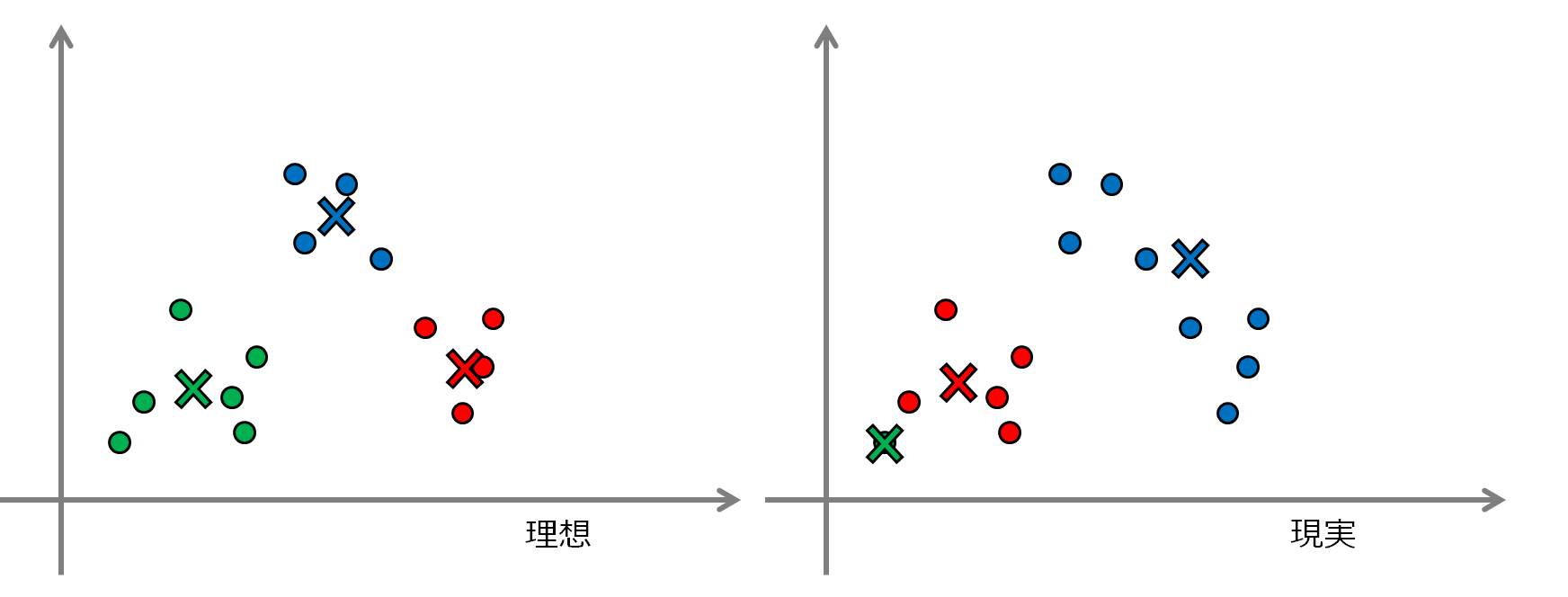
上図左がある種理想的な、こうなってほしいという分割結果で、右が何にも使えそうにない、ある種最悪の分割結果です。
そこで、その現実をできる限り見なくて済むようにと考えられた手法が、重心の初期位置をランダムに初期化するというものです。
実際には、「完全にランダム」というわけではありません。
その手順は、
- データセットの点を、分割したいクラスタの数だけランダムに選択する
- 重心の初期位置を、選択した各点に割り当てる
というだけです。
無論、これだけでは解決できていないことはお判りでしょう。
先の例の、重心位置の偏りを完全に解決することなどできていません。
故に、あと一つ、行うことのできる対策があります。
それが、「繰り返し」です。
言っていることは、簡単に言えば、
「ランダムに初期化していれば、そのすべてで局所最適(上図右)に収束するということは考えにくい」
ので、
「数をこなしてそれっぽいのを選ぼう」
ということです。
あとは、コスト関数Jの値などを見て、採用するクラスタを決めましょう。
クラスタ数の決め方
さて、クラスタリングの手順についての説明はひと段落しましたが、最後に根本を説明しなければなりません。
クラスタリングにおいて、恐らく最も重要な要素は「クラスタの数」、つまりどれだけのクラスタに分割するか決めるというものです。
以下で軽く、その手法について説明しますが、根本的には、「目的に合わせてクラスタ数を選択する」というのが最も正解に近い方法でしょう。
エルボー法
アルゴリズムとして利用可能な例として、エルボー法というクラスタ数決定手法を紹介します。
以下の画像がその基本的な考え方を示したものです。

クラスタ数Kの増加はコスト関数Jの低下に寄与することが想定されます。
クラスタ数の増加は、概ね、あるデータのごく近くに重心が現れる確率を上げます。
故に、その下がり幅の効率が最も良い点、つまり、画像中のグラフにおいて傾きが極端に変化している点(=肘の位置)の数のクラスタに分類するのが、最も効率が良いとする考え方です(この場合は左から三つ目)。
しかし、この方法には欠点があります。以下の画像は、「肘」が存在しない場合の例です。
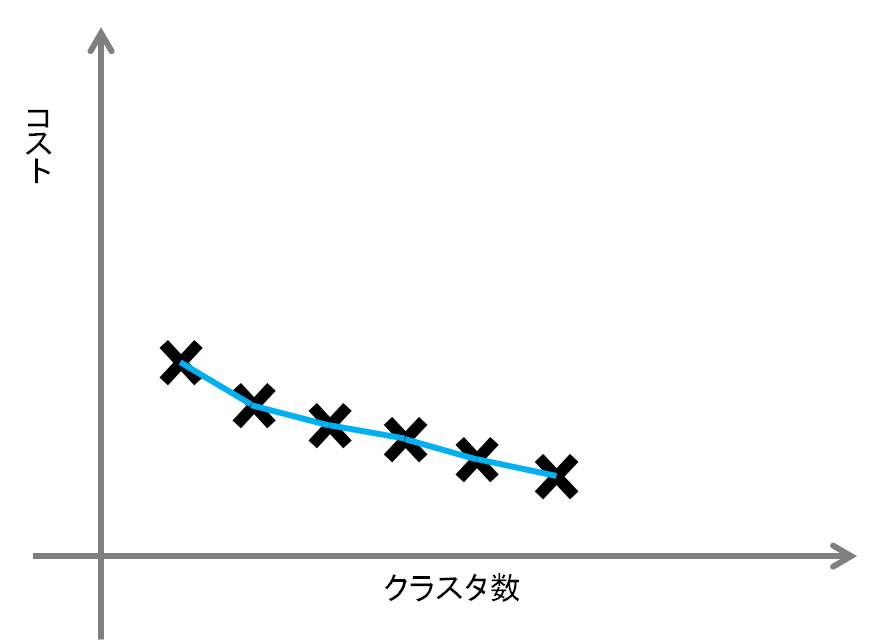
クラスタ数の増加がコストの低下にあまり影響を与えない場合には、このようなグラフになります。
こういった場合には、最も効率の良い点を選択することはできず、エルボー法によって適切なクラスタ数を得るというのは難しい状態であるといえるでしょう。
故に、エルボー法は万能とは言えません。
あくまで、こんな方法がある、程度の認識で結構です。
「目的に合わせる」
もう一つ、ある種こちらが本命ですが、最も効率の良いクラスタ数を得る、最も良い方法は、「目的に合わせる」というものです。
少し身もふたもない方法ですが、服のサイズ分けを例に考えると、分けられるクラスタの数には制約があります。
それは予算であったり、生産設備の問題だったりと、いろいろあるでしょうが、確実に存在します。
しかし、現実としてそういった制約に従っていない、理想だけのクラスタ数を選んでも意味はありません。
例えば、S-M-Lの生産しかできない状況で、XS-S-M-L-XLの5クラスタへの分割などは無意味です。
故に、クラスタリングの目的に応じてクラスタの数を決定するのが近道です。
まとめ
ここまで、「クラスタリング」について説明してきました。
大まかにまとめると、
- クラスタリングは、集団をクラスタに分けるためのもの
- 階層的手法と非階層的手法がある
- クラスタ数は目的に合わせて決める
というあたりを覚えておけば、導入としては十分です。


