LoginSignup
8
7

More than 3 years have passed since last update.

@aya_se

【AtCoder / PAST 2020】とある水色コーダーが最近の精進記録を振り返る【青色になるために】

Last updated at Posted at 2020-08-19

こんにちは。aya_seと申します。2019年3月頃からAtCoderで競技プログラミングをはじめ、現在レートHighest1498です。本格的に過去問での練習(いわゆる「精進」)を開始したのが今年の4月頃のことですが、そこから約4か月でどのような内容を勉強したかについてまとめてみたいと思います。

レート推移・PASTについて

2019年3月～2020年8月現在までの私のAtCoderでのレート推移はこのような感じです。
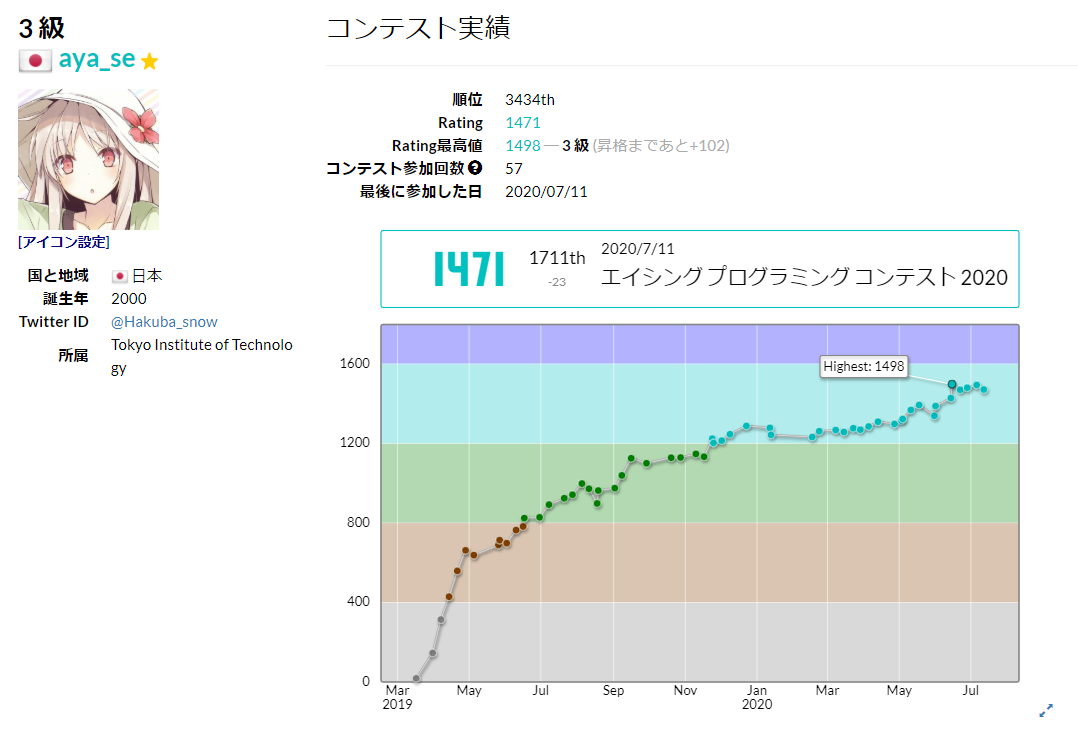
image.png
レーティング1500の壁に苛まれています。助けて下さい(切実)。

また、2020年6月頃に開催されたAtCoder社の提供する資格試験であるPAST(アルゴリズム実技検定)の第3回の無料での通常受験も行いました。結果は上級(88点)でした。PASTはAtCoderの通常のコンテストと比較してひらめきや数学力を必要とする問題が少なく(というよりほぼ無く)、純粋なアルゴリズムの知識や実装力を要する問題が多い印象で、個人的にはPAST型の方が得意なのかもしれません(?)。ただ、エキスパート到達には、あと1問とはいえまだまだ高い壁を感じているところです。

学習したアルゴリズム・テクニックについて

比較的最近学んだアルゴリズムやテクニックをまとめていきます。おそらく大多数は水→青に変色するために必要かもしくは水になる時点で知っておくのが妥当であっただろう水準の知識だと思います。

取り上げる項目一覧

  • bitDP
  • 桁DP
  • 最長部分増加列 (LIS)
  • セグメント木・Binary Indexed Tree
  • 最小全域木 (Kruskal法)
  • 最小共通祖先 (LCA)
  • 座標圧縮 (座圧)
  • 連想配列(std::map)の利用
  • 半分全列挙
  • 最短経路問題 (Dijkstra法・BellmanFord法・WarshallFloyd法)
  • 木の直径
  • 木DP・全方位木DP
  • 最大フロー・最小カット (Ford-Fullkerson法)

bitDP

DP(動的計画法)の1種で、状態を2進数の形で保持するテクニックを指します。巡回セールスマン問題という有名な探索問題でも利用されるアルゴリズムです。DPテーブルは「$dp[i][j]：$$i$番目まで見て状態が$j$であるようなときのある値」となるのが一般的で$j$は2進数の形になります(例：コインが$K$枚ある場合の裏表の状態を$0～2^K-1$で保持する)。

この知識を使う問題例

何か非常に小さい制約の数が与えられた場合にはbitDPの利用を視野に入れるのが良さそうです。bitDPは状態を2進数で管理するため、あまり大きな個数のものの状態の保持には利用できません。特にPASTでは頻出な印象があります。

  • 第一回PAST I - 部品調達
    • 比較的シンプルなbitDPの問題です。
  • 第三回PAST M - 行商計画問題
    • 重実装でいかにもPAST感のある問題です。実行時間制限がややシビア。
    • まずダイクストラ法(後述)でいくらかの最短経路を求めておいた後で、bitDPで最適解を発見するという流れです。

桁DP

DP(動的計画法)の1種で、数字の各桁に注目するような問題に利用されるテクニックです。DPテーブルは$dp[i][smaller][j]$というように設計することが多いです。桁DPの特徴としてはsmallerフラグが挙げられ、例えば「$K$以下の自然数のうち$0$を$C$個含む数の個数を求めよ」といった問題では$i$桁目まで見た時に$K$以下であることが確定しているか、という情報をsmallerフラグで管理するといった具合です。smallerフラグの存在により、$K$以下という制限の中で$i+1$桁目にどの数を使うことが許されるかの範囲を確定できます。

この知識を使う問題例

数の各桁に着目し、かつ$K$「以下」という数の制約があるような問題を見かけたら真っ先に桁DPの利用を検討するべきでしょう。あまり応用範囲が広くはない為、出題頻度はそこまで高くありませんが、直近のABCなどのコンテストでも数回出題実績があります。

  • ABC154 E - Almost Everywhere Zero
    • 桁DPの元祖典型問題と言えるような基本問題です。
  • ABC117 D - XXOR
    • XORなどビット(桁)に着目する題材がテーマの問題では桁DPもセットになりやすい気がします。

最長部分増加列 (LIS)

ある数列の単調増加な部分列(連続していなくてもよい)のうち最長のものを最長部分増加列(LIS)と呼んでおり、DPと二分探索の考え方を組み合わせて$O(NlogN)$で取得できることが知られています。具体的には「$dp[i]：$長さ$i$のLISの末尾としてあり得る最小の数」というようなDPテーブルを考え、さらにこのDPテーブルの値は常に単調増加であることを利用して、値の更新位置を二分探索で決定していきます。知っていないと初見でこの問題を解くのはなかなか難しいと感じます(他にも言えることですが)。

この知識を使う問題例

意外と使うべきタイミングが分かりづらいところはあるのかもしれません(?)

  • ABC006 D - トランプ挿入ソート
    • LISを利用する問題であると気が付くのが難しく、気が付けば一瞬で解けるという昔の過去問にありがちなタイプです。

セグメント木・Binary Indexed Tree

任意の区間和の取得や区間加算の計算、さらに区間における最大値・最小値の取得を$O(logN)$で実行可能なデータ構造です。区間和に関しては累積和でも全く問題ありませんが、区間内最小値・最大値や区間加算が必要な問題に関してはセグ木やBITを知っているかどうかで解けるかどうかが決まると言っても過言ではないように思います。また、想定の本解はセグ木やBIT以外を使うような問題でもセグ木やBITを用いることで無理矢理解くことが出来る、いわゆる「セグ木で殴る」ことによる可能性も広がります。

この知識を使う問題例

セグ木やBITを使う問題は直近のコンテストではかなり頻度が低いように感じます(特にABCでは殆ど出ていない気がします)が、PASTの後半問題(特に上級レベル帯)ではほぼ確実に出題されています。PASTで上級以上を目指す場合には欠かせない知識だと思います。

  • 第二回PAST N - ビルの建設
    • 非常に実装量の多く厳しい問題ですが教育的だと思いました。
    • BITなどを用いた区間加算と座標圧縮(後述)を組み合わせて解きます。
    • 2次元の座標のうち片方は時間軸として捉えて昇順に処理することで実質1次元の問題に帰着します。
  • Donutsプロコンチャレンジ2015 C - 行列のできるドーナツ屋
    • RMQによる最小値の取得とBITによる区間加算を併用して解くことが出来ます。
    • より具体的には$i$番目の人よりも背の高く$i$番目より後ろにいる人のうち最前の人が$i+k$番目である場合、$i$番目の人を観測できる範囲(=出力解を$1$増加させる範囲)は$i+1～i+k$番目に定まるという性質を利用して各地点から見える人数(出力解)をBITで保持、RMQで高さ$h$以上の人でまだ登場していない人のうち最も前にいる人の位置の取得することを考えれば良いです(※解説PDFが存在しないため少し詳しめに書きました)。
  • ABC038 D - プレゼント
    • 一見DPっぽい問題設定ですが、DPは部分点解法です。
    • ビルの建設と同じく、2次元のうち1次元は昇順に見ることで実質1次元の問題に帰着する必要がある点にも注目です。
  • Chokudai SpeedRun 001 J - 転倒数
    • BITを利用する具体的な事例として「転倒数」も挙げられます。転倒数は$A_i>A_j$かつ$i<j$を満たすような数列の数の組み合わせの総数です。BITでは数$i$が既に登場しているかをカウントしておき、$i$番目の数を見た時に、自分より左にある数は最大$i-1$個ですが、このうち$A_i$未満の数の個数を除いたものを転倒数としてカウントしていけばよいです。BITに数$i$が既に登場したかを記録しているため、この値は1回あたり$O(logN)$で取得できるようになっています。

最小全域木 (Kruskal法など)

あるグラフにおいて、一部の辺と全ての頂点を使用し任意の2頂点間が連結であるようなグラフのうち、使用する辺のコストの合計が最小であるものを求めるアルゴリズムです。クラスカル法とプリム法がありますが、実用上はどちらか片方が利用できれば十分だと思います。

この知識を使う問題例

問題を見た時に「これは最小全域木を使う問題だ！」ということには比較的気が付きやすいケースが多く、純粋に知識の有無で差が出る分野だと思います。その性質の為か、PASTでは後半の問題で頻出であるものの、直近のコンテスト(特にABC)ではかなり出題頻度が低い印象です。

座標圧縮 (座圧)

地味ながら非常に重要なテクニックだと考えています。例えば$N$個の点$(1\le N\le10^5)$があり$i$番目の点が座標$A_i$$(-10^9\le A_i\le10^9)$に位置しているという状況下では、各座標についての情報を直接配列で管理することは不可能です(範囲が広すぎる為)。しかしこれらの点の上下関係を維持しつつ座標が小さい順に$1,2,\cdots,N$と番号を割り振って配列で管理すると上手く問題が解けるようになるケースがあります。このように必要な上下関係だけを残して不要な座標情報を削減することを座標圧縮と呼んでおり、連想配列(std::map)などを利用して実装することが出来ます。全体的に実装が重めになることが多いです。

この知識を使う問題例

座標圧縮のみを用いて解くというよりは他のアルゴリズム(特にBITや二分探索)と組み合わせて解くことが多い印象です。全体的に重実装になることが多く、とてもつらいです。

  • ARC075 E - Meaningful Mean
    • BITと座標圧縮を組み合わせて解きます。
    • 個人的にはBITや座標圧縮という発想に至るまでの式変形が数学的で難しいと思いました。比較的古い過去問ですが、直近のABC-Fなどに、どこか近い雰囲気を感じます。
  • 第二回PAST N - ビルの建設
    • 非常に実装量の多く厳しい問題です。
    • BITなどを用いた区間加算と座標圧縮を組み合わせて解きます。

連想配列(std::map)の利用

座標圧縮とも少し重なりますが、連想配列を使えるようになることも現実的には非常に重要だと感じます。要素の取得等に$O(logN)$の時間を要するものの、通常の配列では面倒な処理を非常に簡潔に書けるようになることがあり、直近のAtCoderにおいては連想配列の活用はレーティング向上に直結する要素の1つであると考えています。

この知識を使う問題例

連想配列を使う代表的な事例としては素因数分解が挙げられます。素因数分解のライブラリは手元に持っておくことを強く推奨します。直近のABC-Eなどで連想配列は地味に重要なテーマの1つになっていると思います。

  • ABC152 E - Flatten
    • 素因数が直接テーマになっているわけではないのですが、扱うべき数が大きすぎるために素因数分解の形式で数を管理するという問題です。水difficultyの中ではかなり難しいと思っています。
  • ABC168 E - ∙ (Bullet)
    • 実質的には内積が0になる(=直交する)ベクトルの組み合わせを考える問題であるということに気づく必要があり、難しいです。
    • ベクトルの「傾き」を保管する際に連想配列が有用です。

半分全列挙

制約が少しだけ大きく、完全な全探索は難しいという問題について、問題を半分などに分割して半分だけは全探索を行い、その情報を基に残りの半分についても処理をするというテクニックです。地味でかなり使いづらいテクニックだと思っています。また、「半分を処理する」という性質上、どうしても実装が煩雑になりやすい印象です。

この知識を使う問題例

使うべきタイミングがかなり分かりづらいですが、「半分程度なら全探索しても問題ない」という程度の制約が与えられた場合は注意した方がよさそうです。

  • ABC032 D - ナップサック問題
    • 一見シンプルなナップサックDPをするだけのような印象を受けますが、実はデータセット1だけはナップサックDPでは対応できないという罠があります。$N$の制約が小さいのでここで半分全列挙が活躍します。
    • 半分全列挙した後は残りの半分について二分探索を用いて探索することで全体としては計算量を抑えることが出来ます。

最短経路問題 (Dijkstra法・BellmanFord法・WarshallFloyd法)

グラフの最短経路問題は主に水difficulty以上で頻出の分野です。最短経路を求めるアルゴリズムとしてはダイクストラ法・ベルマンフォード法・ワーシャルフロイド法が挙げられ、それぞれ利用機会が異なります。非常に大雑把に言えば

  • 負の重みの辺や閉路を含まない最短経路問題 → ダイクストラ法
  • 負の重みの辺や閉路を含む最短経路問題 → ベルマンフォード法
  • 全頂点間についての最短経路問題 → ワーシャルフロイド法

というように使い分けることができるでしょう。ワーシャルフロイド法は$O(N^3)$なので$N$の制約はかなり小さいものである必要があります。
また、一般的なグラフの最短経路問題では、ワーシャルフロイド法やダイクストラ法などをシンプルに用いればよいのですが、少し工夫してこれらを利用しないと解けないような問題が出題されることがあります。基本的には、「グラフ上では本来同じ頂点であってもその場の状態に応じて別の頂点と見做す」という考え方です。

この知識を使う問題例

  • ABC164 E - Two Currencies
    • 問題の変数の種類が非常に多く、とてつもなく難しそうに見えます。
    • 初見だと混乱しますが、拡張ダイクストラ法の問題として解くことが出来ます。
  • ABC137 E - Coins Respawn
    • やや設定が煩雑ですが結局はグラフの最短経路問題に帰着できます。
    • ただしこの問題では閉路を含む場合があり、ダイクストラ法は適用できないため、ベルマンフォード法を用いるのが適切です。
  • ARC035 C - アットコーダー王国の交通事情
    • 問題設定からしてワーシャルフロイド法を使うのが良さそうであることはすぐに分かります。
    • 途中で辺が追加されるというのがやや特殊ですが、ワーシャルフロイド法の「経由地点」だけを固定して$O(N^2)$でワーシャルフロイド法をやり直していけば計算量的に十分間に合います。

最小共通祖先 (LCA)

木構造において、ある頂点とある頂点の両方の祖先である(より根に近い)ような頂点のうち、最も2頂点に近いものを最小共通祖先と呼んでいますが、これを任意の2頂点に関して$O(logN)$で取得できるようなアルゴリズムが存在しています。セグ木(RMQ)を用いる手法とダブリングを用いる手法がありますが、自分は後者を使っています(前者は実はまだ勉強していません…)。最小共通祖先自体が重要なテーマである他、これと関連して2頂点間の距離を$O(logN)$で取得することも可能です。

この知識を使う問題例

全体的にそこまで高頻度で問題が出題されるという程ではないが、昔でも最近でも一定の数出題がある印象です。

  • ABC014 D - 閉路
    • 最小共通祖先(LCA)を求める問題であると気づけば一瞬という感じの問題です。
  • 第一回PAST K - 巨大企業
    • 「共通祖先」感は薄い表現ですが、事実上最小共通祖先(LCA)だけでスッキリと判定できます。

木の直径

木構造において全ての2頂点間の中で距離が最長であるものを木の直径と呼びます。求め方は幅優先探索(BFS)を2回行うというもので、1回目は適当な頂点を始点としたBFS、2回目は1回目のBFSで始点から最遠距離であった頂点$A$を始点とするBFSを実行し、その際最遠距離であった頂点$B$を求めます。するとこの頂点$A,B$が木の直径を成す2頂点であり、頂点$A,B$間の距離が木の直径の長さということになります。シンプルではありますが、知っていないと意外と解けない気がするので、地味ながら押さえておきたい知識と言えそうです。

この知識を使う問題例

木DP・全方位木DP

木構造においてDPを行うような際のDPを木DPと呼んでいます。このときDPの更新順序は深さ優先探索(DFS)の帰り掛け順になります(子→親に伝播させていくイメージ)。遷移式は問題によって適宜変えていくしかありません。
また、通常の木DPは始点を1つに固定して行いますが、これを$O(N)$で全始点について求められるようにするのが全方位木DPです。回目は通常の木DPを行い(この際DPの保管方法は$dp[u][i]：$頂点$u$の$i$番目の有向辺の先にある部分木に対応する値というように変更)、その後はBFS順で有向辺の向きを逆転させながらDPを更新していきます。しかし、普通に更新するだけでは計算量が多くなってしまうので、累積和的な考え方を利用して値の取得を高速化する必要があります。正直こちらはまだ自分も理解が十分でないので、今後も学習を続けたいと思います……。

この知識を使う問題例

結構使うタイミングを見極めるのに慣れが必要そうな印象があります。木DPではなく通常のBFSなどによる探索で解けそう！と思ってしまう……。

  • ARC028 C. 高橋王国の分割統治
    • 全方位木DPではない通常の木DPで対処可能
    • 木DPでは2つの情報を保持する必要があります(pair型の配列)。
  • ABC160 F - Distributing Integers
    • 全方位木DPの問題です。難しい。
    • それ以前に木DPをどう遷移させるかの発想が難しいと感じます。場合の数の組み合わせ計算(コンビネーション)に帰着させる考え方が必要……。

最大フロー・最小カット (Ford-Fullkerson法)

始点と終点が与えられたコスト付きの有向グラフにおいて、どのように経路を割り振れば始点→終点に最大の量の「水」を流せるか、すなわち「最大フロー」を求める問題です。これを求める具体的なアルゴリズムにフォードファルカーソン法があり、「始点→終点の経路を1つ発見したら、その際に使用した有向辺の重み分を逆向きに変更する」というループを行える限り行うというものです。また、全ての経路を断つために必要な最小コストである最小カットは実は最大フローと一致することが知られており、この2つは実質同義と言えます(=「最大フロー最小カット定理」)。
また、これと全く同じ考え方で最大二部マッチングの問題も解くことが可能です(マッチさせる対象の他にダミーの始点と頂点を設け、通常の最大フロー問題に帰着させる)。

この知識を使う問題例

直近のAtCoderのコンテストでは出題されているのを殆ど見たことがありませんが、PASTでの出題実績はあるようです。また、現実の問題に応用できることも多いようで、今後AtCoderで増えることが示唆されているマラソン形式のコンテストなどで活躍する機会が多いかも……？？

  • ABC091 C - 2D Plane 2N Points
    • 最大フローの知識は必須ではありませんが、最大二部マッチングの問題としてスマートに解くことも出来ます。
  • ABC010 D - 浮気予防
    • 重みが全て1の場合の最小カット問題です。
    • 与えられるのは無向グラフですが、双方向に有向辺を追加すれば通常通り最大フローの問題として解くことが出来ます。

参考にしている書籍・サイトについて

最後に、学習の際によく利用している書籍やサイトを紹介します。参考になれば幸いです。

おわりに

早く青コーダーになりてぇ～。

8
7
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
7