こんにちは、awakiaです。今回のアドベントカレンダー、結構、機械学習ガチなメンツが揃ったみたいなので、俺も対抗してやる!!とも思ったのですが、研究を離れて2年が経とうとしているので、真っ向勝負とか今更無理なことに気づきました...w
なので、開発者の皆も知っておくと便利なデータサイエンスの話をすることにします。
ABテストと検定の必要性
Webサービスを運営していると、見た目の問題だけでも結構悩みます。ボタンの色や文言などの小さなところから、トップページに盛り込む内容をどうするかまで、いろいろです。
今回、「ABテスト」と呼ぶものは、画面に占める大きさ等にかかわらず、パターンAとパターンBを作って、そのどちらがいいかを判断するための実験と定義することにします。
なお、ABテストの呼び名には結構流派があるので別の名前で聞いたことがあるかもしれません。例えば、Googleのマット・カッツ先生は、Googleが行なっているという少数のユーザーグループに対するテストを「バケットテスト」「クッキーテスト」と呼んでいます。(http://www.suzukikenichi.com/blog/are-google-serps-the-same-on-all-browsers/)
それでは、ABテストを行う際の具体例として、ユーザー登録のボタンの色を赤/青どっちにした方がいいのか迷っているという状況を考えてみます。これを判断するために、半分のユーザーには赤を、もう半分のユーザーには青を見せるという実験をしてみた結果、
赤:120人 vs 青:100人
というデータが得られたとしましょう。
この瞬間、あ、「赤」の方がいいのね。「赤」に決定! データ主義バンザイ!!
となったあなたは幸せです。もう赤いボタンにするといいと思います。
実際、赤いボタンの方がいい可能性は、統計的にどう解釈しても高いです。
でも、もし
- 自分もしくはチームの誰かが統計的に意味のあるデータしか信じない
- 実は自分は青の方が好きで、出来れば赤にしたくない
といった状況に置かれてしまった場合、もう少し粘って考えてみましょう。
ちなみに裏話として、こういったデータ主義は、とてもデザイナー泣かせです。一生懸命、全体のバランスを考えてサイトデザインをし、色も選んでいるのに、「データが他の色がいいことを示している( ー`дー´)キリッ」などと言われて、センスの無いエンジニアに色を変えられたのでは、プライドもズタボロでしょう。
でも、実際、この場合エンジニアの方が正しくない?と言う意見もありですが、例えば、楽天市場のホームページってなんかごちゃごちゃ(ごめんなさい、ごめんなさい、悪気は無いんです)していますが、実は、あれ、すっきりしたデザインに変えてみたら急激にクリック率、購入率が下がったので、ごちゃごちゃしたのに戻したという、まことしやかな都市伝説が流れています。
統計的に検証してみる
さて、話を戻しましょう。
先ほど得られた、赤が120人、青が100人という結果を用いて、赤いボタンの方が良いと結論付けるためには、この結果が「たまたま起こったわけじゃない!」と言い切る必要があります。
これを言い切れるようにしてくれる方法が、統計学の(有意性)検定と呼ばれもので、これが分かれば「結果に有意差がある/はない!」などと言うことが出来るようになります。
じゃぁ、実際に検定をやってみようと思っても、統計検定のWikipediaカテゴリには、網羅率の低いWikipedia日本語版でも28項目(すべてが統計検定の手法なわけではないですが)、Wikipedia英語版では約100項目と、正直どれ使えばいいんだ!!状態になっています。
有名なものをとってみてもT,Z,F,U,G検定という英語一文字のものや、χ2検定などというギリシャ文字を使ったものまであり、もう世の中の人を惑わすために名付けたとしか思えない惨状を目のあたりにするはずです。
でも大丈夫!
ABテストの結果の検証するためには、**符号検定**だけ知っていればOKです。
符号検定は、http://aoki2.si.gunma-u.ac.jp/lecture/Average/sign-test.html に
対応のある 2変数の組について,母代表値に差があるか検定する。
2変数の組で単に,いずれが優れているか劣っているかあるいは同等であるかしかわからないときに適用する
と書かれているように、ABテストにピッタリで、パターンAの方が良かったら+、悪かったら-という符号を付けてカウントし、それぞれの個数の差に意味があるかを検証する検定法なんだなと考えれば、"符号"検定というのも思い出しやすいのではないかと思います。
蛇足:検定の一般論
一般に検定を行うためには、以下の2つを定める必要があります。
- 検証したい仮説がどんな分布に従うか
- 確率何%をあり得ないかとみなすか
1.については、例えば、PCのハードディスクが壊れてしまう現象はポアソン分布に従うと言われています。
今回のABテストに関しては、パターンAとパターンBに違いが無いとみなした場合、コインを投げて表と裏が出る回数を記録していった時の分布と同じとみなせるので、それは(成功確率p=0.5の)二項分布と呼ばれる分布です。
2.は有意水準と呼ばれ、慣習として5%か1%が使われます。あくまで慣習で、科学的根拠はありません。更にABテストでは、間違った結論を出しても大して困らないので、1%を使うことはあまりなく、5%の方が使われることが多い気がしています。
なので、「検定結果に有意差があります」と言われたら、「パターンAとパターンBは同等だとみなしたら、5%以下の確率でしか起きないことが起きてしまってるんだよね。これってもうパターンAとパターンBに明確な違いがあるって言ったほうが自然じゃない?」と言われたと思えばいいことになります。
符号検定をしてみる
さて、
赤:120人 vs 青:100人
という結果で、赤ボタンの方が本当に良いと言えるか検定してみましょう。それにはR言語のpbinomを使って、以下のように計算します。
> pbinom(120-1, 120+100, 0.5)
[1] 0.9
この0.9と言う数字は、青ボタンでも赤ボタンでもユーザー登録率は同じだとした時に、赤ボタンを押される回数が220回中、120未満(0-119回)でありえる確率を表しています。
この時、有意水準を5%としても、1 - 0.05 = 0.95に達していないので、有意に赤ボタンの方が良いとは言えないということになります。残念でした。
ちなみに、220人中何人が赤ボタンをクリックしていたら有意と言えたかというのは、qbinomを使うとわかって
> qbinom(0.95, 120+100, 0.5)
[1] 122
122+1の123人であれば有意であったということになります。
このRの結果は、220回中、赤ボタンが0回押される確率から122回押される確率まで全て足し合わせると全体の95%に到達するということを表します。なので赤ボタンが123回以上押される確率は、5%に満たない(=ありえない)事が言えます。ありえないことが起こったら、赤と青の効果が等しいという前提が間違ってたということなので、123回であれば有意だったんですね。
実際に、足し合わせる関数であるpbinomを用いて確かめると、
> pbinom(121, 120+100, 0.5)
[1] 0.9396072
> pbinom(122, 120+100, 0.5)
[1] 0.9541673
なので、122ではじめて0.95を超えてますね。
有意水準1%だとどうなるかというと、
> qbinom(0.99, 120+100, 0.5)
[1] 127
128人必要です。
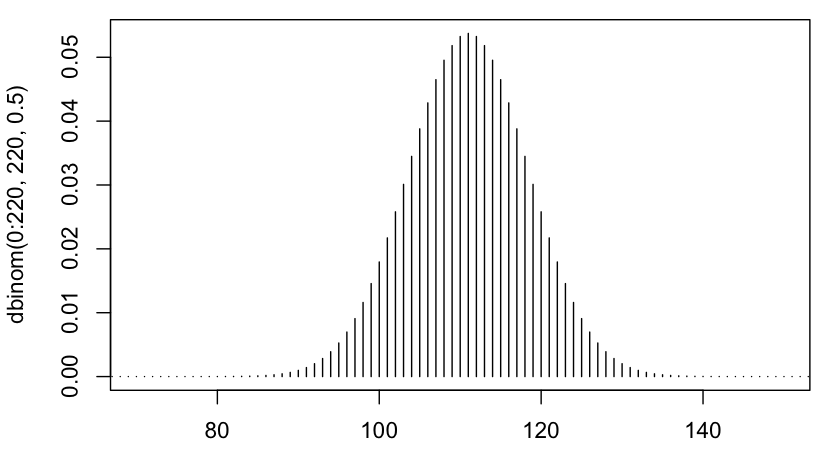
更に、この二項分布がどういう形をしているのか見てみるには、plotとdbinomを使って
> plot(dbinom(0:220, 220, 0.5), type="h", xlim=c(70,150))
と入力すれば、
と表示され、120のあたりがどのくらいありえそうか可視化することができます。
Rに関して話をすれば、検定を直接行なってくれる関数binom.testも存在して、以下のように使うことができます。
> binom.test(120, 220, 0.5, "greater")
Exact binomial test
data: 120 and 220
number of successes = 120, number of trials = 220, p-value = 0.1
alternative hypothesis: true probability of success is greater than 0.5
95 percent confidence interval:
0.4878 1.0000
sample estimates:
probability of success
0.5455
p-value = 0.1と言う部分が、先ほどの0.9と言う値を、全体の1から引いた値に対応していますね。
まとめ
ABテストでの有意性検定には符号検定 (半々で実験しない場合は、より一般に二項検定と呼ぶ)を用いるとよい。
具体的には、以下の(クリック、ユーザー登録等の)アクションがあったとき、
| アクション数(回) | 実験対象の割合 | |
|---|---|---|
| パターンA | a | p (0.5, 0.01等) |
| パターンB | b | 1-p |
二項分布を用い、以下のように検定する。
significance = 1 - pbinom(a-1, a+b, p) >= 0.95
注) a+bが大きすぎる場合、教科書的には、二項分布だとnCkの計算が必要なため計算できなくなる&正規分布に高精度で近似できるので、正規分布を用い検定するとあるが、Rを用いると、別に二項分布でもかなりの大きい数に対して計算が可能なので常に二項分布を使っておけば良い。
> pbinom(110000020, 220000000, 0.5)
[1] 0.5011028
最後に
ABテストはとても実用的で強力なツールです。でも、ABテストに頼りすぎて、データに踊らされることのないように注意して欲しいと思います。
- ユーザー獲得は決してコインの裏表の回数と同一ではありません。仮にあるデザインの方がユーザー数は獲得できるとしても、もう一方のデザインの方が質の良いユーザーを獲得出来る可能性があることを忘れてはいけません。
- 統計的に有意などと言っても、結局は仮定と解釈の産物です。都合のいいデータが出た時に使って、自分の主張を有利にしましょう。