MPPICInterFoamのチュートリアル探索

MPPICInterFoam

MPPIC(Multiphase particle-in-cell method:多相)とは、粒子-流体連成計算法の一つです。

粒子法としてよく知られたものにDEMがあり、CFD-DEMとして個体粒子-流体の連成計算に用いられているようですが、計算負荷がとても高い方法になります。この方法で波打ち際の砂の運動を計算するのは現実的ではありません。
　そこで代替の方法として挙がってくるのがMPPIC法です。この方法は多数の粒子をすべてラグランジュ粒子として計算するのではなく、粒子分布を補完関数で代用して計算負荷を低減する方法です。

このソルバーはVOF法かつMPPIC法を使うことが出来ます。このチュートリアルケースの改造を最終的な目標にして記事を書いていこうと思います。

twoPhasePachuka

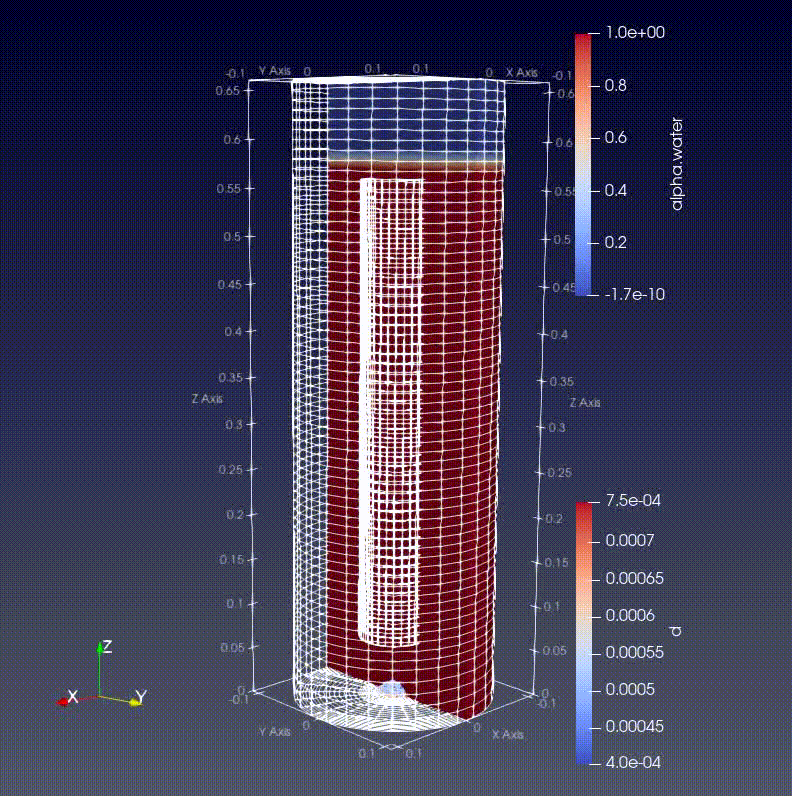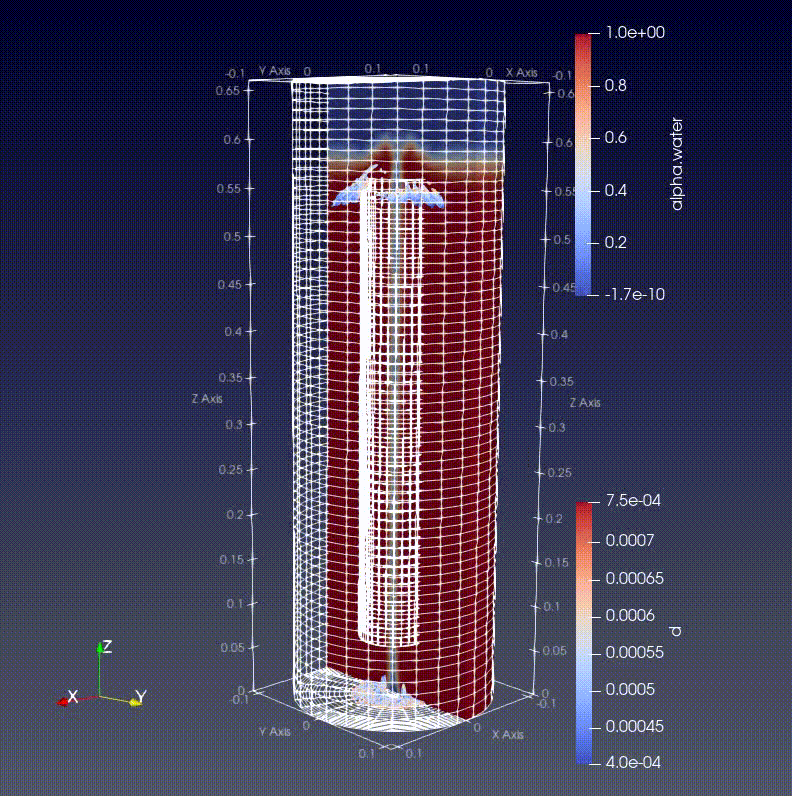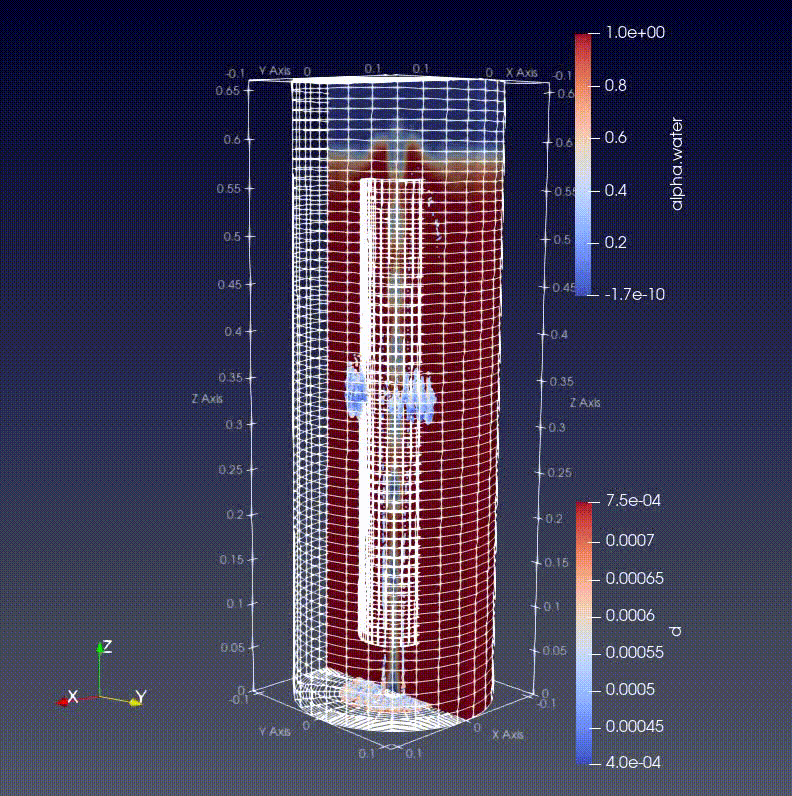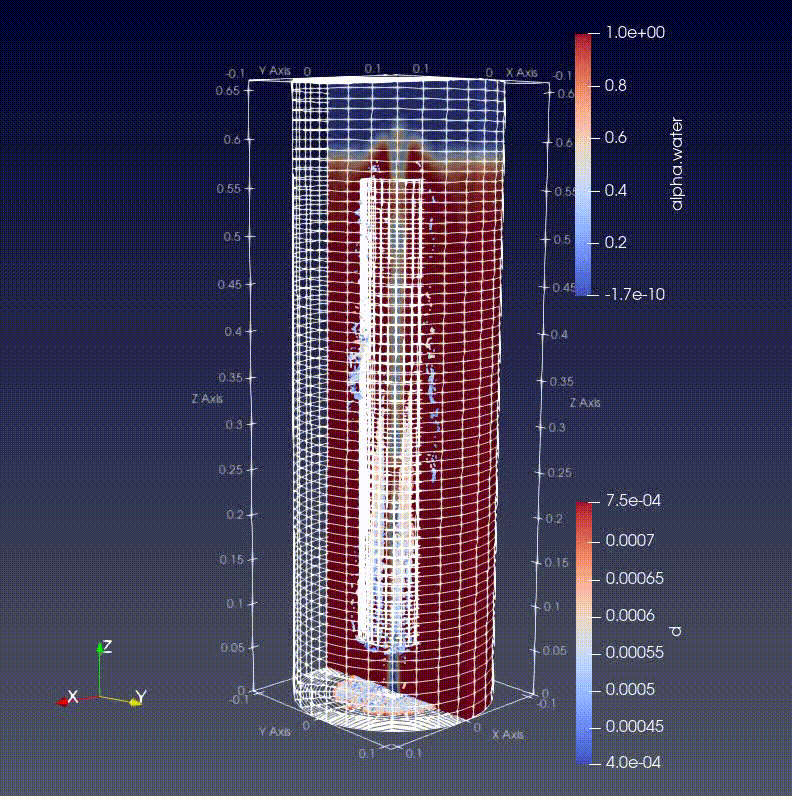
モデルは底面の真ん中あたりに設定したinlet面から空気と粒子を同時に液体内に吹き込んでいます。
液体は初期にある界面をもって存在しています。

暇が出来たら追記していきます

※pachukaをグーグル検索してみると、以下のようなバルブの一種らしい。どう使うのこれ

チュートリアルの中身

0.orig
->alpha.water
->epsilon
->k
->nut
->p_rgh
->U

constant
->g
->kinematicCloudProperties
->transportProperties
->turbulenceProperties

system
->blockMeshDict
->createPatchDict
->fvSchemes
->pachuka.m4
->topoSetDict
->controlDict
->decomposeParDict
->fvSolution
->setFieldsDict

どう改造したいか

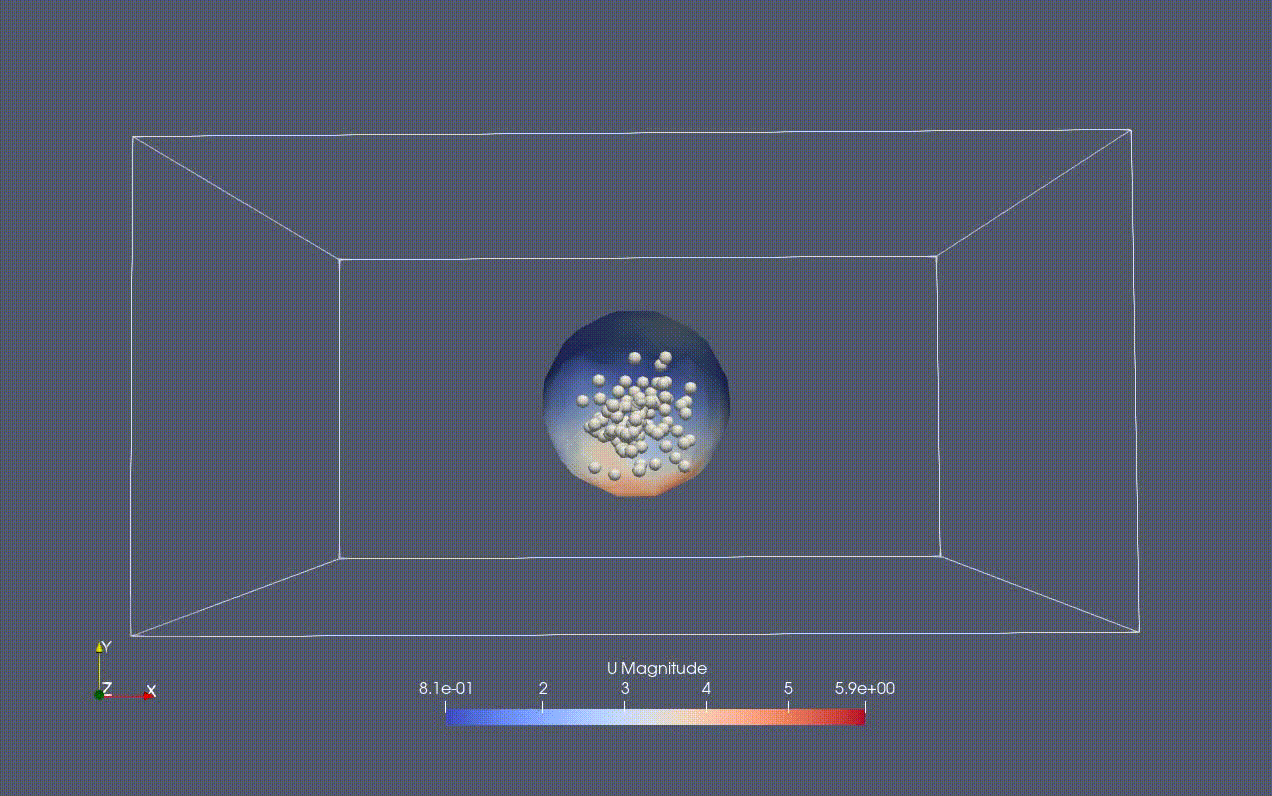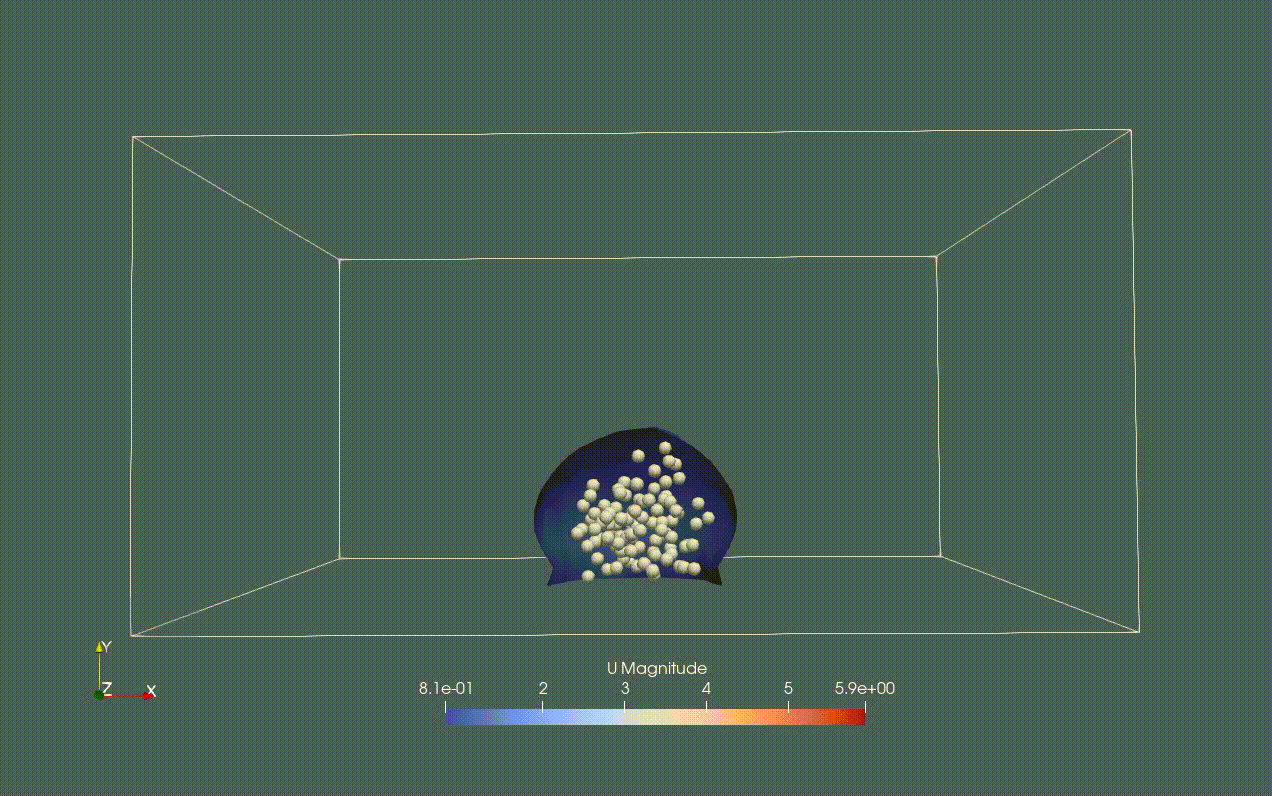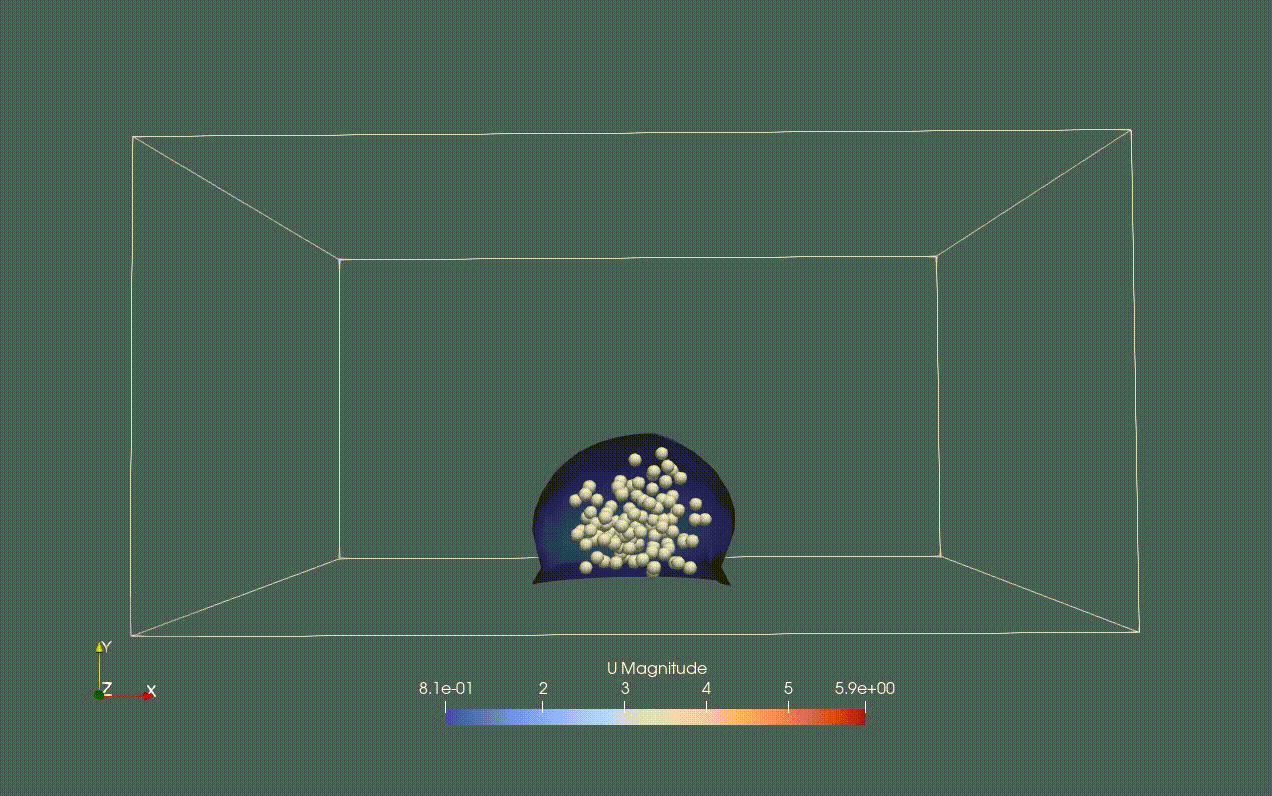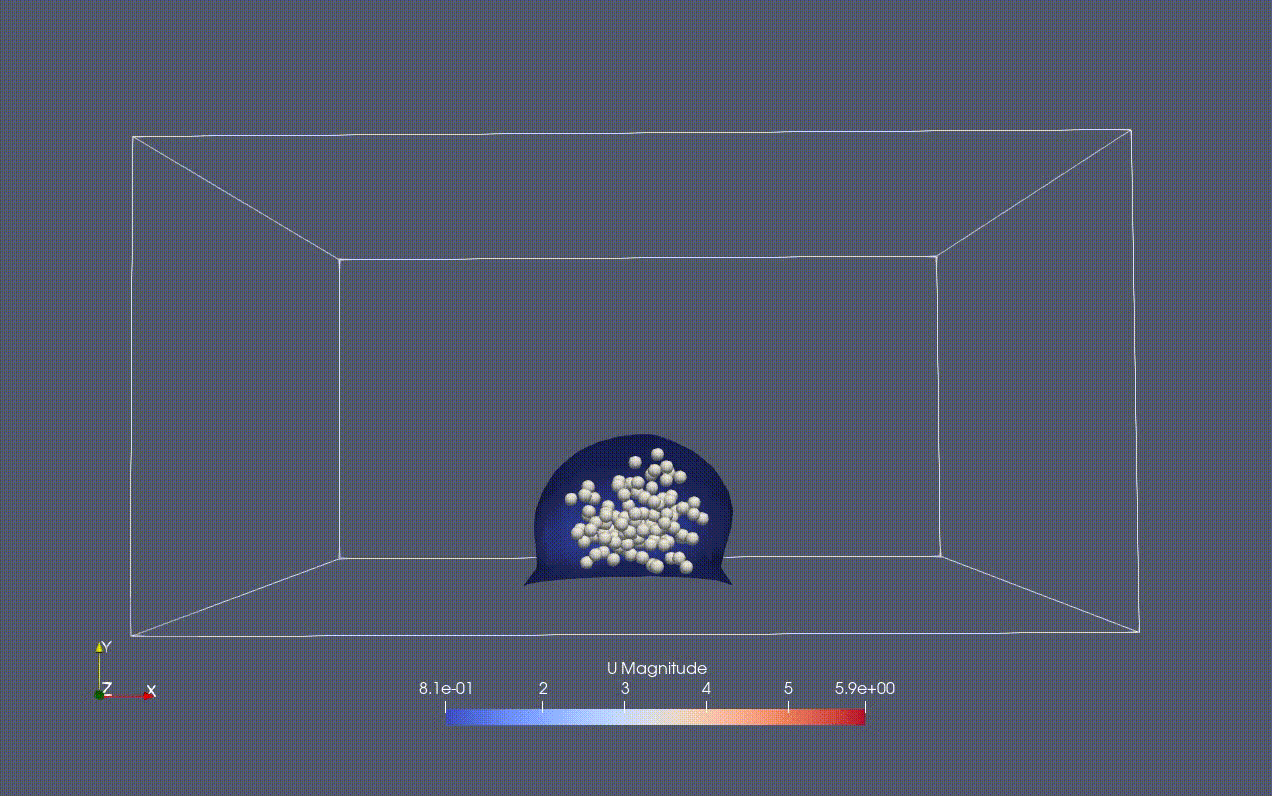
1. 液体領域を液滴とする
   →setFieldDictに書き込む

FoamFile
{
    format      ascii;
    class       dictionary;
    location    "system";
    object      setFieldsDict;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

defaultFieldValues
(
    volScalarFieldValue alpha.water 0

regions
(
    sphereToCell
    {
        centre (-0.01 0.004 -0.01);
        radius 0.003;
        fieldValues
        (
            volScalarFieldValue alpha.water 1
        );
    }
)

1. 初めから液滴内部に粒子が存在するようにする
   →tutorials/laglangian/MPPICFoam/colume/constantに含まれるkinematicCloudPositionsに粒子ごとにxyz座標を書き込む

import random

def generate_points_in_sphere(center, radius, num_points):
    points = []
    x1, y1, z1 = center
    
    for _ in range(num_points):
        # 3次元球内のランダムな座標を生成
        phi = random.uniform(0, 2 * 3.141592653589793)  # Φ (azimuthal angle)
        costheta = random.uniform(-1, 1)  # cos(θ)
        u = random.uniform(0, 1)  # ランダムな値
        
        theta = 1.0 - u
        theta = theta if theta <= 1 else 1.0
        theta = theta if theta >= -1 else -1.0
        theta = math.acos(theta)  # θ (polar angle)
        
        # 球座標系から直交座標系へ変換
        x = x1 + (radius * math.sin(theta) * math.cos(phi))
        y = y1 + (radius * math.sin(theta) * math.sin(phi))
        z = z1 + (radius * math.cos(theta))
        
        points.append((x, y, z))
    
    return points

def save_to_dat_file(points, filename):
    with open(filename, 'w') as file:
        for point in points:
            file.write(f"({point[0]} {point[1]} {point[2]})\n")

if __name__ == "__main__":
    import math
    
    center = (1, 2, 3)  # 中心座標 (x1, y1, z1)
    radius = 5  # 半径 r
    num_points = 100  # 生成する座標の数
    
    # 球内の座標を生成
    points = generate_points_in_sphere(center, radius, num_points)
    
    # datファイルに保存
    save_to_dat_file(points, "output.dat")

2023/12 改造

MPPICInterFoamとInterFoamのチュートリアルを参考にして改造