最急降下法 (バッチ勾配降下法)
簡単なイメージ
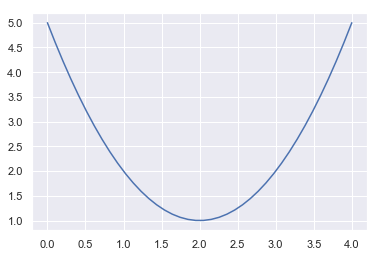
- 今、$x$の2次関数$f(x)=x^2-4x+5$をイメージしてみます
- この関数をグラフにすると以下の様になります
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set()
x = np.linspace(0, 4, 40)
y = x**2 - 4*x + 5
plt.plot(x, y);
この関数の最小値を求める際に、関数の一回微分(導関数)=0となる点を求める方法があります。中学生で習った方法です。こうすれば一発で最適解が求まります。しかし、機械学習では変数やデータの数が非常に多く、一発で最適解を求めることが困難な場合もあります。この時に活躍するのが勾配降下法です。
今、ランダムな点$(x, f(x))$を選びます。その点における接戦の傾きを調べ、傾きがゼロに近づくように$x$の値を更新していきたいと思います。仮に初期値が$(4, 5)$だとした場合、この時の接戦の傾きは$f'(1) = 4$であることが分かるかと思います。
- この時x軸方向に傾きと逆の方向に$x$の値を更新すれば傾きが少なくなることが分かる
- $-4$だけ動くと逆に更新しすぎてしますので、何かしらの定数(一般に学習率と呼ばれる)をかけた値で更新する
$$ x_{i+1} = x_i - \eta\frac{d}{dx}f(-4) \eta … 学習率$$
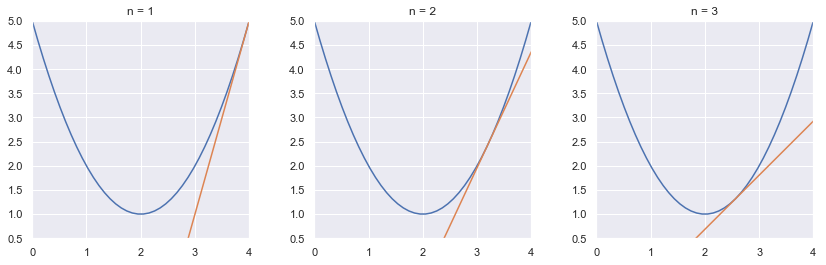
図でイメージしてみたいと思います
# 二次関数を定義
def f(x):
return x**2 - 4 * x + 5
# 1次導関数を定義
def df(xx):
return 2 * xx -4
# 接戦の方程式を定義
def tangent(x, xx):
a = df(xx)
b = f(xx) - a * xx
return a * x + b
# xxの更新(pathへ格納)を定義
def gradient_descent(xx, eta=0.1, n_iter=3):
path = []
for _ in range(n_iter):
grad = df(xx)
path.append(grad)
xx = xx -eta * grad
return path
x = np.linspace(0, 4, 40)
xx = 4 # 初期のx座標
# x座標の更新
path_list = gradient_descent(xx)
# 図示
fig, axes = plt.subplots(1, 3, figsize=(14, 4))
plt.subplots_adjust(wspace=0.3)
for i in range(3):
axes[i].set_title('n = {}'.format(i+1))
axes[i].set_xlim([0, 4])
axes[i].set_ylim([0.5, 5])
axes[i].plot(x, f(x))
axes[i].plot(x, tangent(x, path_list[i]))
最急降下法アルゴリズムの実装
- 二変数関数の最急降下法アルゴリズムを実装します
class GradientDescent:
def __init__(self, f, df, eta=0.05, eps=1e-6):
self.f = f # 最適化する関数
self.df = df # 関数の勾配(1次導関数)
self.eta = eta # 学習率
self.eps = eps # 学習のストップ判定に用いる定数
self.path = None # 学習の経過、初期値は空
def solve(self, x):
path = []
grad = self.df(x) # 勾配
path.append(x)
# 多変数の場合のノルムの大きさとself.epsを比較
# self.epsの二乗より大きい場合、xの更新を続ける
while (grad**2).sum() > self.eps**2:
x = x - self.eta * grad
grad = self.df(x)
path.append(x)
self.path_ = np.array(path) # 学習の経過
self.x_ = x # 最適化された変数の値
self.opt_ = f(x) # 最適化後の f(x)の値
self.grad_ = grad # 最適化後の勾配
実際に計算してみる
- 上記のクラス(最急降下法)を用いて、$x$と$y$の二変数関数を最適化してみます
- $f(x, y) = 6x^2-xy+y^2+x+2y$を使います
- それぞれの偏微分は以下の通りになります
$$\frac{\partial}{\partial x}f(x, y) = 12x -y +1$$
$$\frac{\partial}{\partial y}f(x, y) = -x +2y + 2$$
def f(xy):
x = xy[0]
y = xy[1]
return 6*x**2 - x*y + y**2 + x + 2*y
def df(xy):
x = xy[0]
y = xy[1]
return np.array([12*x - y + 1, - x + 2*y + 2])
gd = GradientDescent(f, df)
initial = np.array([1, 1])
gd.solve(initial)
np.set_printoptions(precision=7, suppress=True) # 有効桁数の設定
print('更新後の変数: {}'.format(gd.x_)) # 更新後の変数: [-0.173913 -1.086956]
print('更新後のf(x,y): {:.3}'.format(gd.opt_)) # 更新後のf(x,y): -0.238
print('更新後の勾配: {}'.format(gd.grad_)) # 更新後の勾配: [0.0000001 0.000001 ]
plt.plot(gd.path_[:, 0], gd.path_[:, 1]); # 更新を図示
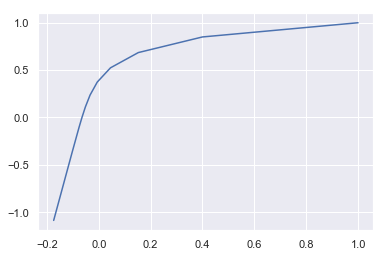
少しずつ収束しているのが分かります
学習率 $\eta$ の値を操作すると収束の経過が変化します
gd_2 = GradientDescent(f, df, eta=0.01)
initial = np.array([1, 1])
gd_2.solve(initial)
print(len(gd.path_)) # 154
print(len(gd_2.path_)) # 796
plt.plot(gd_2.path_[:, 0], gd_2.path_[:, 1]);
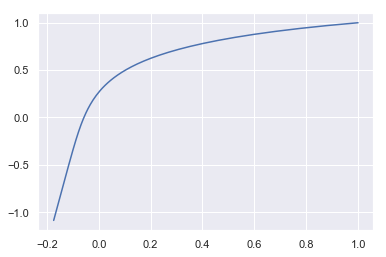
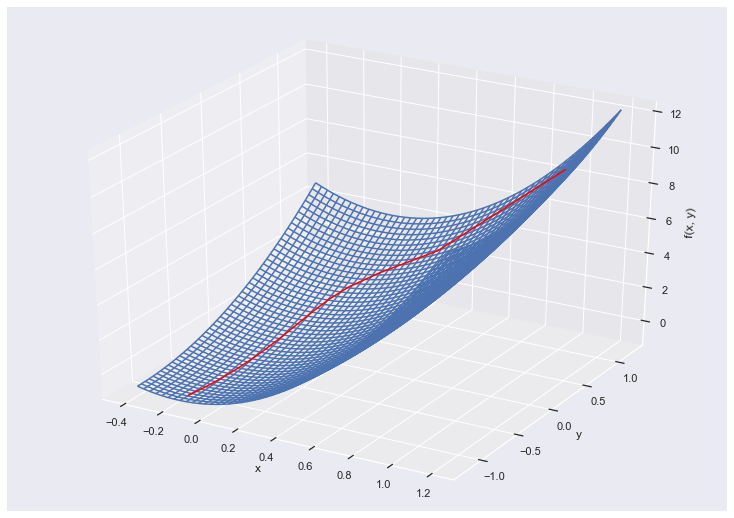
最適化されるまでの更新回数が多く、また曲線の変化も滑らかであることが分かります。上記プロットにz軸を加えた3Dプロットでその軌道を確認してみます
from mpl_toolkits.mplot3d import Axes3D
# pathのプロット
x_path = gd.path_[:, 0]
y_path = gd.path_[:, 1]
z_path = f(np.array((x_path, y_path)))
fig = plt.figure(figsize=(10,7))
ax = Axes3D(fig)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("f(x, y)")
ax.plot3D(x_path, y_path, z_path, color='red')
# f(x, y)曲面のプロット
x_curve = np.linspace(-0.4, 1.2, 50)
y_curve = np.linspace(-1.2, 1.2, 50)
X_curve, Y_curve = np.meshgrid(x_curve, y_curve)
Z_curve = f(np.array((X_curve, Y_curve)))
ax.plot_wireframe(X_curve, Y_curve, Z_curve);
…いまいちイメージつかないので等高線で表現してみます
# 等高線のプロット
x = np.linspace(-1.5, 1.2, 50)
y = np.linspace(-4, 2, 50)
xmesh, ymesh = np.meshgrid(x, y)
z = f(np.array((xmesh, ymesh)))
levels = [-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7]
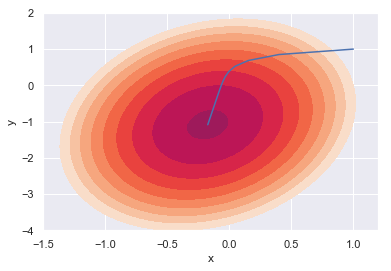
plt.contourf(x, y, z, levels=levels)
# x, y 軌跡のプロット
plt.plot(gd.path_[:, 0], gd.path_[:, 1])
plt.xlabel('x')
plt.ylabel('y');
$f(x, y)$を最小化させる方向に$x$と$y$の値が更新されていることが分かります
次は学習率の値を変えて収束の様子をみてみます
gd_3 = GradientDescent(f, df, eta=0.15)
initial = np.array([1, 1])
gd_3.solve(initial)
print(len(gd.path_)) # 154 eta 0.05
print(len(gd_3.path_)) # 81 eta 0.15
# 等高線のプロット
x = np.linspace(-1.5, 1.2, 50)
y = np.linspace(-4, 2, 50)
xmesh, ymesh = np.meshgrid(x, y)
z = f(np.array((xmesh, ymesh)))
levels = [-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7]
plt.contourf(x, y, z, levels=levels)
# x, y 軌跡のプロット
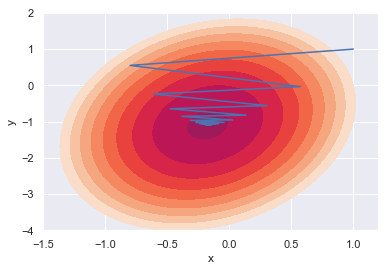
plt.plot(gd_3.path_[:, 0], gd_3.path_[:, 1])
plt.xlabel('x')
plt.ylabel('y');
暴れながらも収束している様子が分かります。学習率が大きいと収束まで早くたどり着けたり、局所的最適解に陥る可能性が少なくなったりといったメリットもある一方、思わぬ方向に発散してしまう可能性もあります。