Kaggle - House Prices挑戦記③：ランダムフォレスト回帰

0. はじめに

Kaggleの有名なコンペティション、House Pricesの挑戦記録です。
この記事のモチベーションについては挑戦記の第一部で触れているので、そちらをご覧ください。

とにかくあらゆる作業とその理由・思考を言語化しようというのがこの記事での目論見で、「Kaggleに勝つ」「ハイスコアを目指す」ことを主眼に置いてはいません。一つひとつの作業や試行を真の意味で理解をするために、このコンペに関する他の記事はいっさい参照していません。

前回は、Ridge回帰でベースラインモデルを作成しました。ベースライン時点でもRMSEが0.14程度とまあまあだったのですが、今回はランダムフォレストモデルを作成していこうと思います。

1. ランダムフォレスト実装

前回のベースラインモデルの実装において、部分的に類似したさまざまな特徴量を、正則化によって多重共線性をある程度回避しつつモデルを構築しました。
今回実装するランダムフォレストについては、以下のようなメリットがあります。

• ノンパラメトリックな手法（対象のデータ分布を仮定しない）
• カテゴリカルデータにも強い
• 多変数が複雑に関連し合っている場合、単純な線形モデルよりも決定木モデルのほうが精度が高い場合がある
• 特に、変数同士の非線形な関係を捉えやすく、交互作用の検出力高

ただし、以下のようなデメリットにも注意が必要です。

• モデルの複雑性が増す
• ハイパーパラメータがブラックボックス化しやすい

線形回帰モデルの一種であるRidgeでは、カテゴリカルなデータをターゲットエンコーディングによって係数化して扱いましたが、決定木系のアルゴリズムではカテゴリカルなデータをそこまで複雑な特徴量操作をせずとも扱うことができるのもいいですね。

1.1 特徴量作成

それでは、決定木系モデルが扱いやすいようにモデルを構築していきます。
この一連の記事の目的は、思考の言語化ともう一つにさまざまな特徴量エンジニアリング手法のショーケースもあります。今回はone-hotエンコーディングといった手法を試していきたいと思います。

データのインポート

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

from constants import * # パスなどの定数をインポート

plt.style.use('ggplot')
sns.set_palette('flare')

# 1から特徴量を作成するため、生のデータを取得
raw_data = pd.read_csv(os.path.join(RAW_PATH, 'train.csv'), index_col=0)
raw_data.head()

それでは、RFR（ランダムフォレスト回帰）用にデータを整形していきます。順序・名義尺度はダミー変数化するため、基本的な数値特徴量のみ、前回までを参考にして作成します。

# 空のデータフレームを作成
all_data = pd.DataFrame()

# 前回までを参考に特徴量を作成
raw_data['log_price'] = np.log(raw_data['SalePrice'])

all_data['MSSubClass'] = raw_data['MSSubClass'].astype(str)

all_data['log_price'] = raw_data['log_price']

all_data['total_sf'] = raw_data['1stFlrSF'] + raw_data['2ndFlrSF'].fillna(0) + raw_data['TotalBsmtSF'].fillna(0)

all_data['log_total_sf'] = np.log(all_data['total_sf'])

all_data['has_2nd'] = (raw_data['2ndFlrSF'] > 0).astype(int)

all_data['has_bsmt'] = (raw_data['TotalBsmtSF'] > 0).astype(int)

all_data['has_garage'] = (raw_data['GarageArea'] > 0).astype(int)

all_data['has_pool'] = (raw_data['PoolArea'] > 0).astype(int)

all_data['has_central_air'] = (raw_data['CentralAir'] == 'Y').astype(int)

all_data['has_fireplace'] = (raw_data['Fireplaces'] > 0).astype(int)

all_data['house_age'] = raw_data['YrSold'] - raw_data['YearBuilt']

all_data['remod_age'] = raw_data['YrSold'] - raw_data['YearRemodAdd']

all_data['total_porch_sf'] = raw_data['OpenPorchSF'] + raw_data['EnclosedPorch'].fillna(0) + raw_data['3SsnPorch'].fillna(0) + raw_data['ScreenPorch'].fillna(0)


from sklearn.preprocessing import StandardScaler

std_scaler = StandardScaler()

neighbor_log_price = raw_data.groupby('Neighborhood')['log_price'].mean().sort_values(ascending=False)

neighbor_log_price_stdsclaled = std_scaler.fit_transform(neighbor_log_price.values.reshape(-1, 1))

neighbor_log_price_dict = dict(zip(neighbor_log_price.index, neighbor_log_price_stdsclaled))

all_data['neighbor_weight'] = raw_data['Neighborhood'].map(neighbor_log_price_dict).astype(float)


year_price = raw_data.groupby('YearBuilt')['SalePrice'].mean()

year_price = year_price.rolling(window=5, center=True).mean()

year_price = year_price.interpolate(method='linear')

year_price = year_price.fillna(raw_data.groupby('YearBuilt')['SalePrice'].mean())

all_data['year_price'] = raw_data['YearBuilt'].map(year_price)

次に、生のデータから直接使うもの、one-hotエンコーディングするものを取得します。
そして、欠損データを基本的にはそれらの設備等の「不在」と解釈し、欠損値をそれぞれ補填します。

cols = [
    'MSZoning', 'OverallQual', 'OverallCond',
    'ExterQual', 'ExterCond', 'BsmtQual', 'BsmtCond',
    'KitchenQual', 'Utilities', 'PoolQC', 'Functional', 
    'GarageCars', 'GarageQual','GarageCond', 'LotFrontage'
    ]

all_data[cols] = raw_data[cols]

# 欠損値を補填
all_data['LotFrontage'].fillna(0.0, inplace=True)
all_data['Utilities'].fillna('None', inplace=True)
all_data['KitchenQual'].fillna('TA', inplace=True)
all_data['Functional'].fillna('None', inplace=True)
all_data['GarageCars'].fillna(0, inplace=True)
all_data.info()

# Index: 1460 entries, 1 to 1460
# Data columns (total 29 columns):

次に、カテゴリカルなデータを全てone-hotエンコーディングしていきます。

data = pd.get_dummies(all_data, drop_first=True, dtype=int)
# drop_fisrt=Trueで、カテゴリの最初の一つを除いて全てをエンコーディング

data.info()
# Index: 1460 entries, 1 to 1460
# Data columns (total 68 columns):

カラムが68まで増えました。

1.2 プレーンなRFRを実装

さて、ここまで特徴量をそろえたところで、ハイパーパラメータをいっさいチューニングしない、プレーンなRFRを実装してみます。
まずは、訓練データとテストデータの分割から。

from sklearn.model_selection import train_test_split

X = data.drop('log_price', axis=1)
y = data['log_price']

X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=87)

それでは、さっそく学習させていきましょう。

from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import root_mean_squared_error, r2_score

test_rfr = RandomForestRegressor(random_state=0, n_jobs=-1)
test_rfr.fit(X_train, y_train)

y_pred = test_rfr.predict(X_val)

rmse = root_mean_squared_error(y_val, y_pred)
r2 = r2_score(y_val, y_pred)

print('Test RFR')
print(f'  RMSE: {rmse:.4f}')
print(f'  R2: {r2:.4f}')

• 結果:
  RMSE - 0.1176
  R2 - 0.8932

かなりいいスコアが出ましたが、ランダムフォレストは過学習しやすいことは念頭に置いておいてもいいかもしれません。
予測値と実測値で回帰直線を見てみましょう。

sns.regplot(x=y_val, y=y_pred, scatter_kws={'s': 20, 'alpha': 0.3}, line_kws={'color': 'green', 'lw': 1, 'alpha': 0.8})
plt.title(f"Test Random Forest Regr. ")
plt.show()

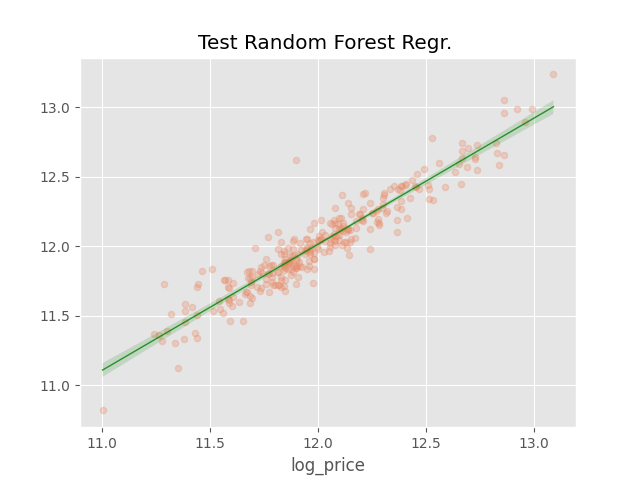
プロットを見ると、かなり的確に予測できていそうですね。
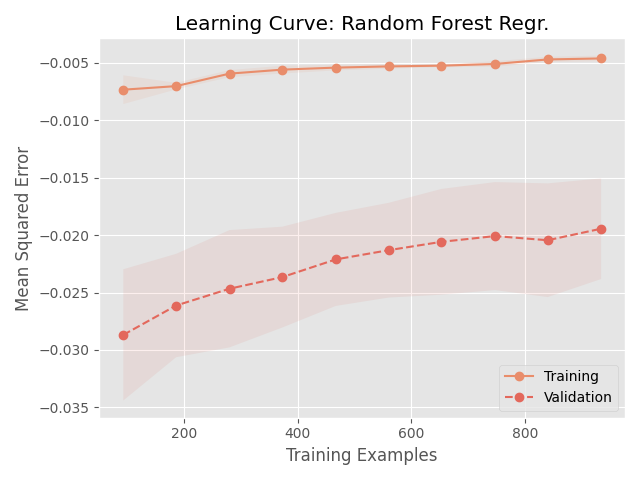
学習曲線を見てみましょう。前回、学習曲線を作成する関数を作成していたので、そちらを呼び出して使います。

from utils import plot_learning_curve

X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)

plot_learning_curve(RandomForestRegressor(n_jobs=-1), X_train, y_train)
plt.savefig(os.path.join(IMAGE_PATH, '0201_learning_curve.png'))
plt.show()

学習曲線からは、訓練データと検証データでMSEの差がかなり大きいことが読み取れます。だいぶ過学習気味です。とはいえ、実際のRMSEスコアは0.11程度なので、それでも悪くはないのですが。
次に、特徴量の重要度を可視化していきます。

plt.figure(figsize=(12, 10))
feature_importances = test_rfr.feature_importances_

importance = pd.DataFrame({
    'feature': X.columns,
    'importance': feature_importances
    }).sort_values('importance', ascending=False)
    
sns.barplot(x='importance', y='feature', data=importance)
        
# 軸ラベルとタイトル
plt.xlabel('Importance')
plt.ylabel('Features')
plt.title('Test RFR: Learning Curve')
plt.tight_layout()
plt.show()

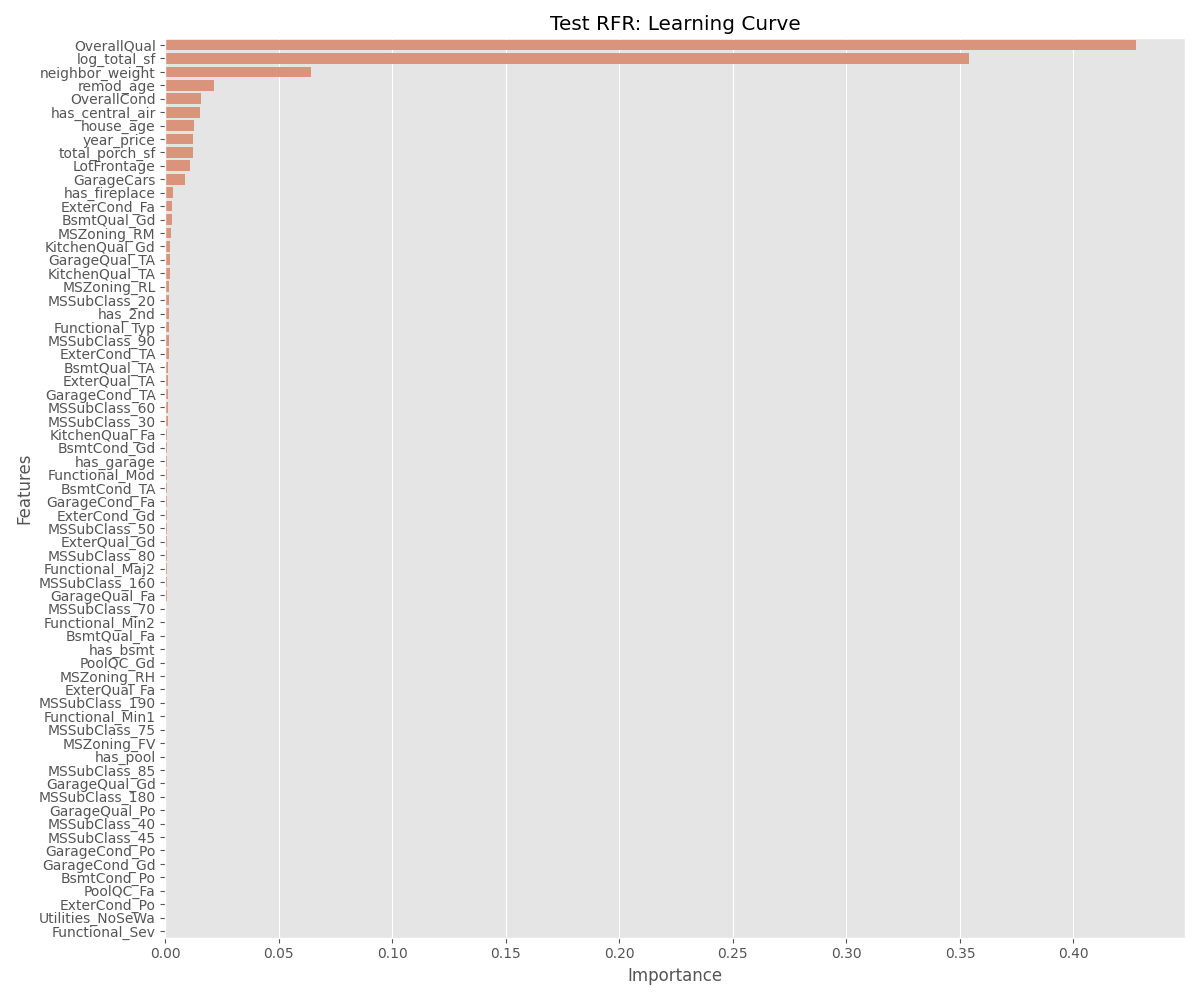
やはり、全体的な品質と広さ、立地、年代というわかりやすい指標がモデルにとり重要であることが確認できます。

2. Optunaハイパーパラメータチューニング

さて、次はOptunaを使用してRFRのハイパーパラメータを調整していきたいと思います。
Optunaはハイパーパラメータの自動最適化フレームワークで、ベイズ最適化を利用することで、パラメータの探索を効率的に行うことができます。

2.1 学習目的の作成

Optunaは、objecvitve()関数を作成し、調整したいパラメータの範囲を指定すると、その範囲内でパラメータの最適な値を探索してくれます。説明するより見た方が早いと思います。

import optuna # インポート

X = data.drop('log_price', axis=1)
y = data['log_price']

# データ分割
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)

# 学習目的を定義
def objective(trial):

    # どのパラメータにおいて最適化を行うか
    params = {
        # 決定技の数を5~150の間で探索、以下同様
        'n_estimators': trial.suggest_int('n_estimators', 5, 150), 
        'max_depth': trial.suggest_int('max_depth', 3, 30),
        'min_samples_split': trial.suggest_int('min_samples_split', 2, 20),
        'min_samples_leaf': trial.suggest_int('min_samples_leaf', 1, 10),
        # 特徴量数、特徴量数の平方根、log2、1/2、1/3で探索
        'max_features': trial.suggest_categorical('max_features', [None, 'log2', 'sqrt', X_train.shape[1]//2, X_train.shape[1]//3]),
        }

    # 探索したパラメータでインスタンス化
    rfr = RandomForestRegressor(
        **params,
        n_jobs=-1,
        )

    # 学習を実行
    rfr.fit(X_train, y_train)

    # 予測を実行し、スコア（今回はRMSE）を算出
    y_pred = rfr.predict(X_val)
    rmse = root_mean_squared_error(y_val, y_pred)

    # スコアを返す
    return rmse

上のように、指定したパラメータの範囲内で最適なパラメータを探索してくれます。同じ範囲でGrid Searchをしようものなら、とんでもない計算量になるのは想像に難くないと思います。

2.2 最適化の実行と可視化

最適化を実行します。

study = optuna.create_study(direction='minimize') # スコア（RMSE）の最小化を目標とする学習を作成

study.optimize(objective, n_trials=300, n_jobs=-1) # 試行300回で最適化を実行

M1モデルのMacBook Proで、大体35秒ほどで探索が終了しました。とんでもない早さですね。
ただし注意点があり、グリッドサーチによる総当たりと異なり、確率論的な最適化であるため、局所最適解に陥る可能性があります。グリッドサーチでおおよその範囲を推定したあとで、Optunaによる細かい最適化を行った方が、探索範囲によっては有効かもしれません。

それでは、最適化されたパラメータととスコアを見てみましょう。

study.best_params, study.best_value

• 出力
  ({'n_estimators': 65,
  'max_depth': 15,
  'min_samples_split': 3,
  'min_samples_leaf': 2,
  'max_features': 22},
  0.12999299058113295)

決定技は65本、最大の深さ15、最大特徴量数は総特徴量数の1/3(22)などが最適と判断したようです。
なお、スコアは0.13と、生のRFRよりは悪化しましたが、最大深度を設定したことで過学習を抑制した結果であり、ベースラインモデルよりはいいスコアが出ているため問題なしとします。

Optunaには、ハイパーパラメータチューニングがブラックボックス化しないための視覚化の手法が多くありますので、それぞれ見てみましょう。

optuna.visualization.plot_param_importances(study)

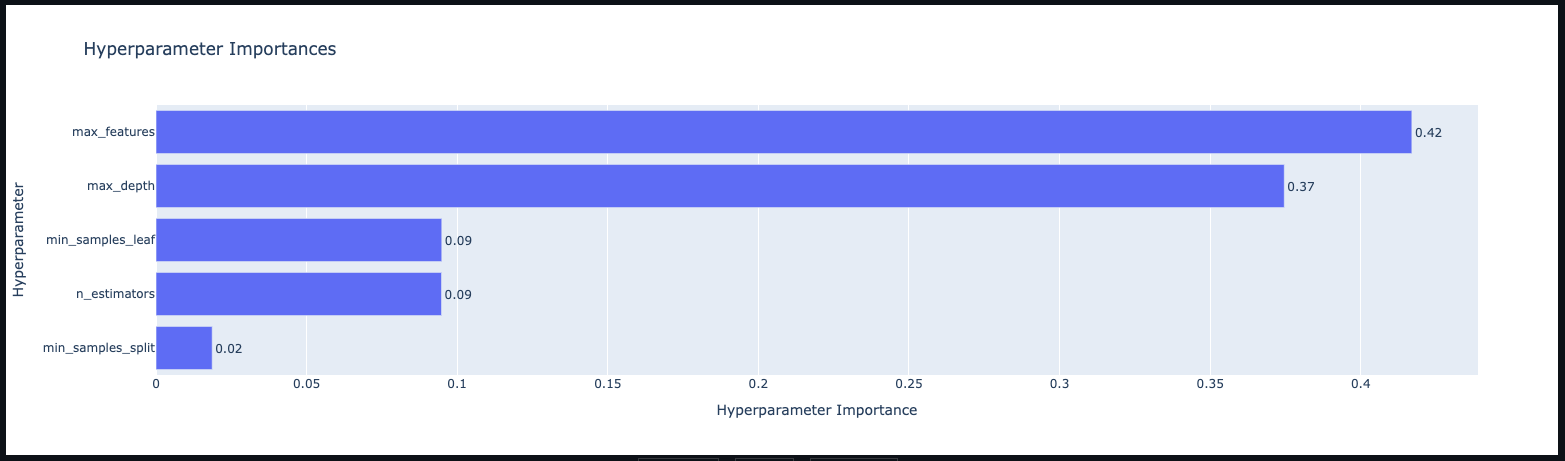
この図は、どのパラメータが重要かをfANOVAというアルゴリズムを用いて算出したもので、各パラメータの分散の大きさを元に算出されるそうです。
最大特徴量数（max_features）と最大深度（max_depth）が、このモデルにとり重要であることがわかります。
次に、最適化の過程を見てみます。

optuna.visualization.plot_optimization_history(study)

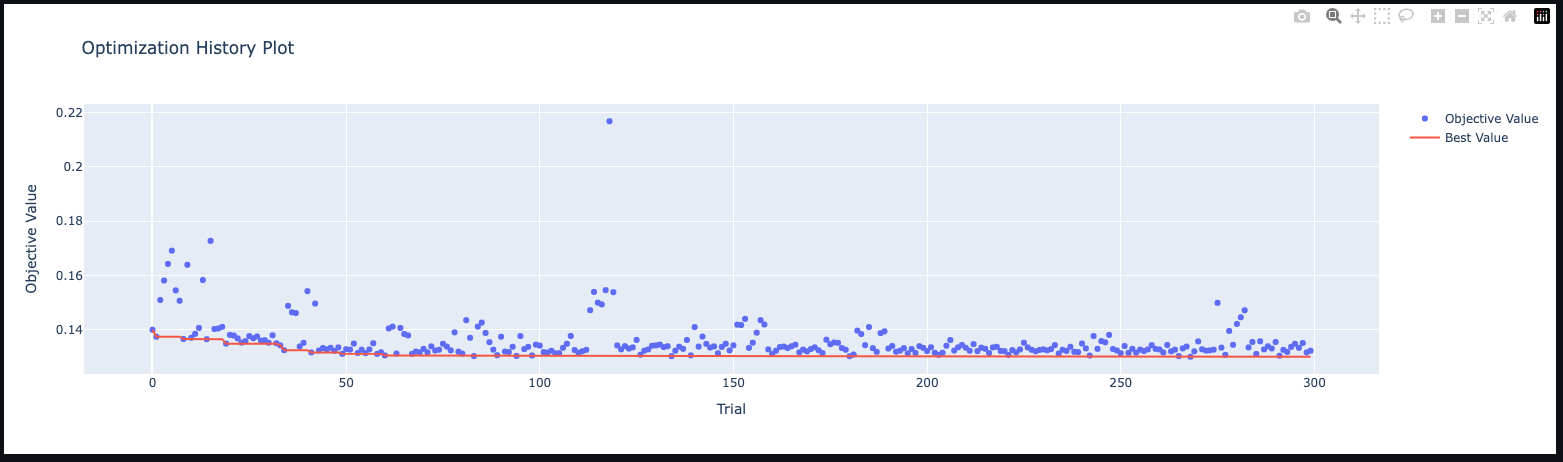
比較的早い段階（試行50）で収束していますが、その後も緩やかにスコアが下がっていっているのがわかります。

3. 最適化パラメータでモデル構築

最適化したパラメータでモデルを作成しましょう。

X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)

# 最適化パラメータを変数化
best_params = study.best_params

# 最適化パラメータでインスタンス化
best_rfr = RandomForestRegressor(**best_params, n_jobs=-1)
best_rfr.fit(X_train, y_train)
y_pred = best_rfr.predict(X_val)

rmse = root_mean_squared_error(y_val, y_pred)
r2 = r2_score(y_val, y_pred)

print('Best RFR')
print(f'  RMSE: {round(rmse, 4)}')
print(f'  R2: {round(r2, 4)}')

• 出力
  RMSE: 0.139
  R2: 0.868

ベースラインに比べてだいぶ改善しました。
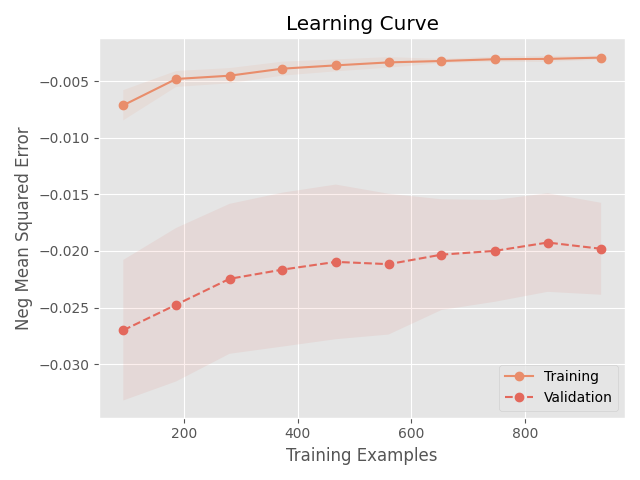
学習曲線を見てみましょう。

from utils import plot_learning_curve

X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=1)

val_rfr = RandomForestRegressor(**study.best_params, n_jobs=-1, random_state=2)

plot_learning_curve(val_rfr, X_train, y_train, title="Learning Curve: Random Forest Regr.")
plt.show()

相変わらず過学習気味ですが、それでもだいぶ検証データでのスコアは上がっています。

最後に、モデル、モデルのパラメータ、スコアを保存します。

import joblib

# モデルの保存
joblib.dump(best_rfr, os.path.join(MODEL_PATH, '0200_rf_regr.joblib'))

# パラメータとスコアの保存
metrics = {
    'model': 'RFR',
    'params': f'{study.best_params}',
    'RMSE': round(rmse, 4),
    'R2': round(r2, 4)
}

metrics = pd.DataFrame(metrics, index=[0])

ridge_metrics = pd.read_csv(os.path.join(METRICS_PATH, '0100_metrics.csv'), index_col=0)

metrics = pd.concat([ridge_metrics, metrics])

metrics.to_csv(os.path.join(METRICS_PATH, '0200_metrics.csv'))

次回は、XGBoostでも同様の作業をしたのち、提出用データを作成しようと思います。