初めに
本記事は時系列解析手法の一つであるSARIMAモデルをpythonのstatsmodelsで実装するまでの流れをまとめたものになります。
学んだことをアウトプットすることを目的として作成しました。
目次
- 1. 定常性とは
- 2. ホワイトノイズ
- 3. SARIMAモデルとは
- 1.ARモデル
- 2.MAモデル
- 3.ARMAモデル
- 4.ARIMAモデル
-
- SARIMAモデル
- 4. SARIMAモデルの実装
1. 定常性とは
時系列解析を語る上で欠かせないものの一つに定常性があります。定常性とは、ある時系列データの値$Y$が、どの時点$t$においても平均、分散、自己共分散が一定であるという性質のことです。これは弱定常性とも言います。
簡単にいうと、各時点での値がある値を中心にばらついているということです。
2.ホワイトノイズ
ホワイトノイズとは、平均が0、全ての時点で自己共分散が0である定常性を持った系列のことをいいます。
時系列分析では、モデルが説明できなかった誤差項がホワイトノイズの性質を持っていると仮定しています。
3. SARIMAモデルとは
SARIMAモデルとは、自己回帰モデル(ARモデル)と移動平均モデル(MAモデル)と和分モデル(I)を組み合わせた自己回帰和分移動平均モデル(ARIMAモデル)に季節的な周期変動を取り入れたモデルです。
SARIMAモデルの理解には上記のモデルの理解が必要不可欠なので、まずはそれらのモデルについて説明します。
1. ARモデル
ARモデルは、自身の過去の値で回帰を行うことで現在の値を予測するというモデルになります。式で表すと次のようになります。
$$
Y_t = c + φ_1Y_{t-1} + ε_t
$$
ここで$Y_t$は時点$t$での値、$c$は定数項、$φ$は係数、 $ε_t$はホワイトノイズに従う誤差項を表しています。
上の式は、一つ前の時点の値から現在の値を予測しています。このようなARモデルをAR(1)過程といいます。
2. MAモデル
MAモデルは、過去の誤差の積み重ねにより現在の値を求めるというモデルになります。式で表すと次のようになります。
$$
Y_t = c + φ_1ε_{t-1} + ε_t
$$
ARモデルと比較すると、係数$φ$が過去の値$Y_{t-1}$ではなく、過去の誤差項$ε_{t-1}$にかかっていることがわかります。この式はMA(1)過程ともいいます。
3. ARMAモデル
ARMAモデルはARモデルとMAモデルを組み合わせたモデルになります。式で表すと次のようになります。
ARMA(1,1)過程ともいいます。
$$
Y_t = c + φ_1Y_{t-1} + ε_t + θ_1ε_{t-1}
$$
4. ARIMAモデル
時系列データによっては、その系列が定常性を満たさず、階差をとった系列が定常性を満たすものもあります。そのような時系列データについてはARIMAモデルを使用することができます。式で表すと次にようになります。
$$
ΔY_t = c + φ_1ΔY_{t-1} + ε_t + θ_1ε_{t-1}
$$
ここでの$ΔY_t$は$Y_t - Y_{t-1}$のことです。このようなARIMAモデルをARIMA(1,1,1)過程といいます。(AR = 1、 I = 1、 MA =1 )
5. SARIMAXモデル
この記事では扱いませんが、SARIMAモデルに説明変数を加えたSARIMAXモデルも存在します。
4. SARIMAモデルの実装
pythonでは、statsmodelsというライブラリを使うことでSARIMAモデルを実装できます。
まず今回使用するライブラリをインポートし、データを読み込みます。この記事で使用するデータは気象庁ホームページからダウンロードした2017年1月~2022年3月15日までの東京都の気温データです。気温データ以外にも降水量や日照時間といったデータも含まれていますが、今回は使用しません。
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import japanize_matplotlib
import statsmodels.api as sm
from statsmodels.tsa.seasonal import seasonal_decompose
df_tokyo = pd.read_csv('tokyo.csv',index_col="年月日", parse_dates=True)
気温についてグラフを作成し可視化します。
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 15, 6
y = df_tokyo["平均気温(℃)"]
y.plot()
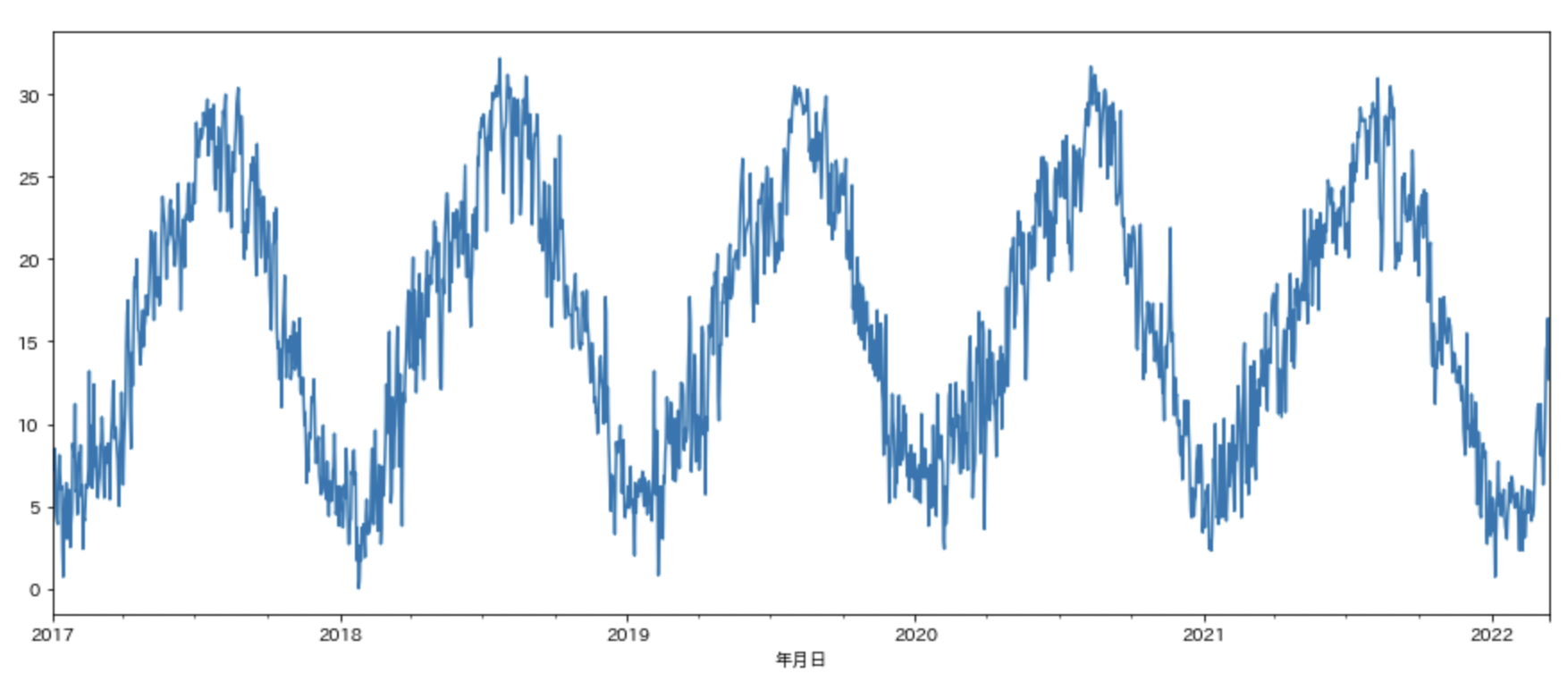
日本には季節があるので、グラフは周期的なものになります。
次に自己相関係数と偏自己相関係数を可視化します。
fig_1 = sm.graphics.tsa.plot_acf(y, lags=400)
fig_2 = sm.graphics.tsa.plot_pacf(y, lags=50)
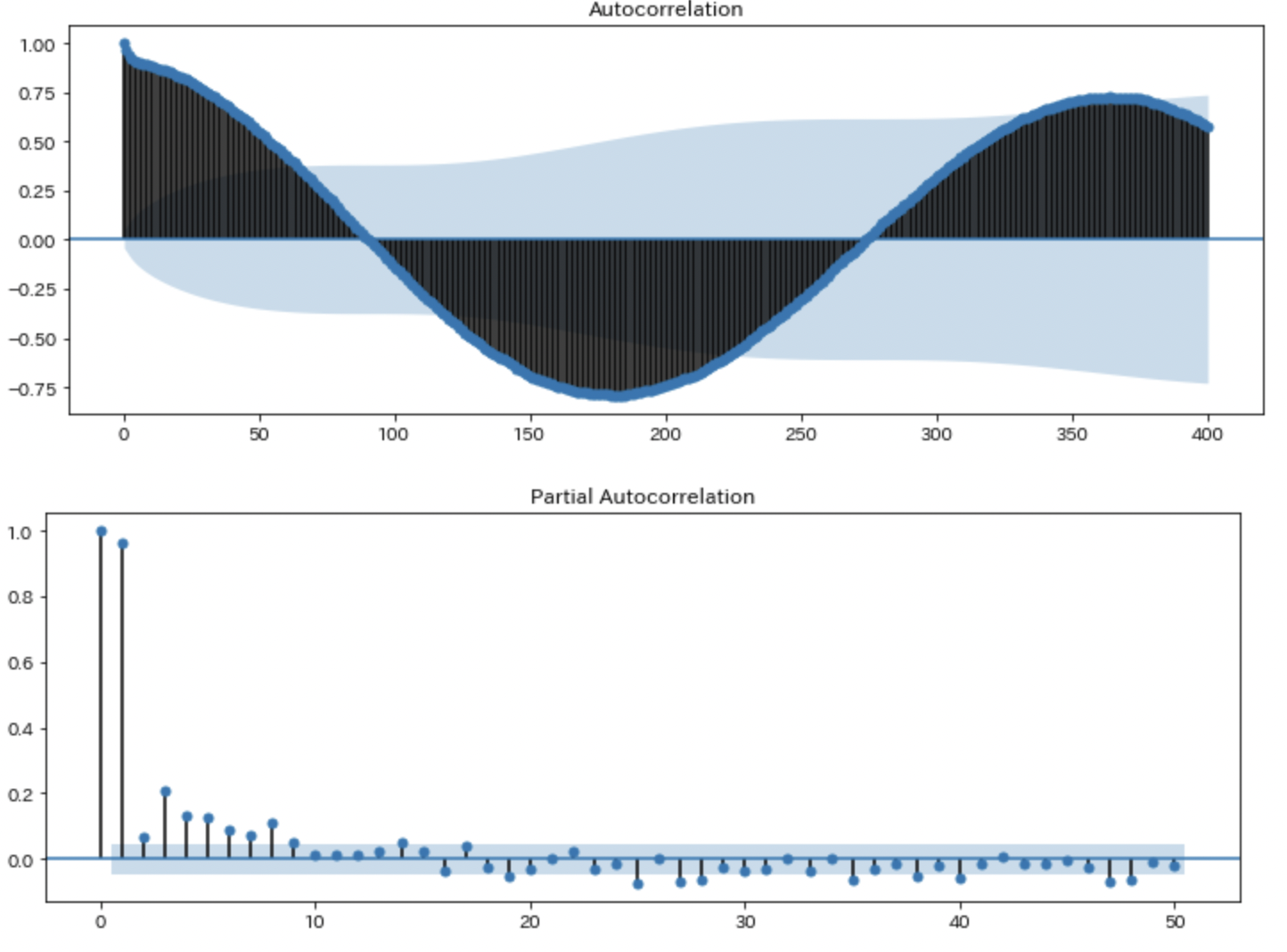
上のグラフは自己相関係数のコレログラムで、下の図は偏自己相関係数のコレログラムです。この図からラグ10で偏自己相関係数が0になることがわかります。
次に波形分解をしてみます。
result = seasonal_decompose(y, period=365, two_sided=True)
result.plot()
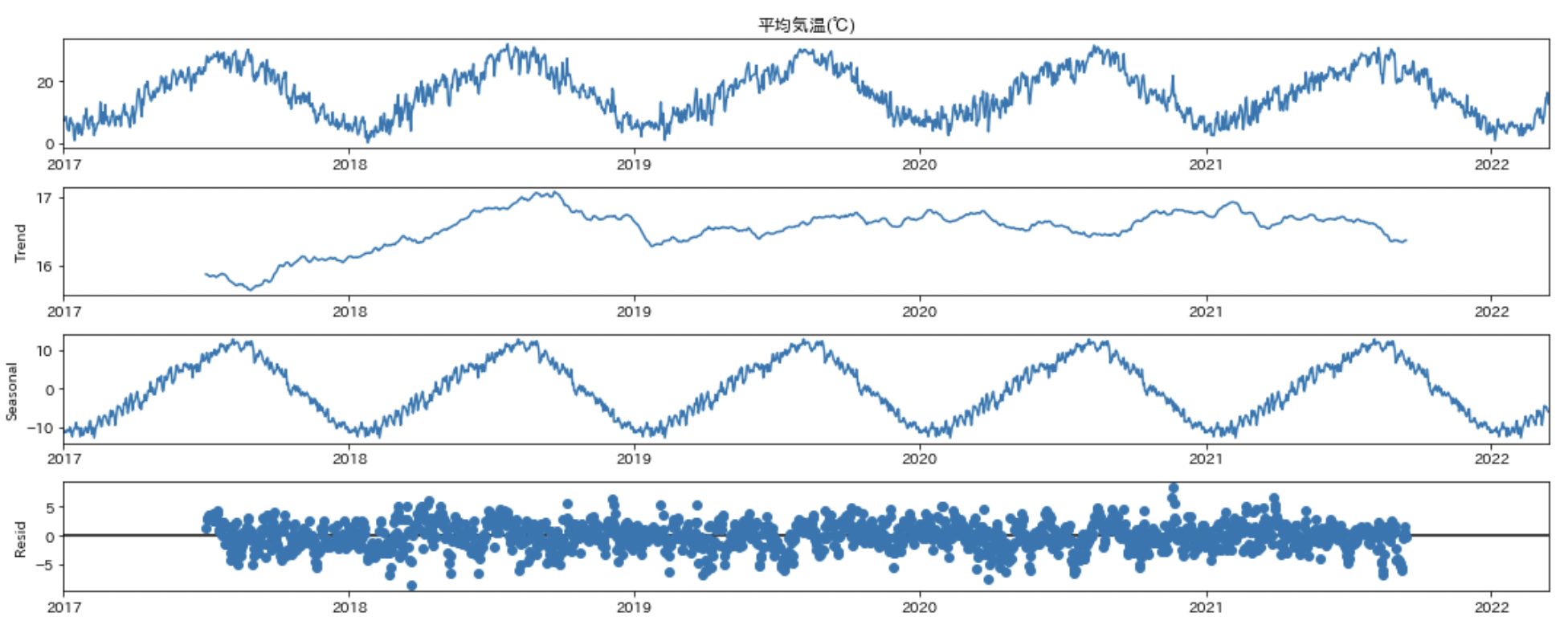
seasonal_decomposeの引数periodは、自分で周期を指定する必要があります。先ほどのコレログラムからも365日周期であることが考えられるので period=365 と指定していいでしょう。
出力結果の一番上のグラフは元データ、二番目のグラフは周期性を除いたデータ、三番目は周期性を表すグラフ(今回は365と指定しているので365周期のグラフになっています)、四番目は残差のグラフになります。
波形分解をするとデータの周期性を除いた傾向がわかります。上の例で言うと、傾向のグラフを見ることで、2017年あたりはそれ以降の年に比べて全体的に気温が低かったことがわかります。
次にSARIMAモデルを実装していきます。
(と、言いたいところだったのですが、365周期で学習を行うと計算に時間がかかり過ぎてしまうので、月ごとにデータを取り直して実装していきたいと思います。)
データの後ろ12ヶ月分のデータをテストデータとし、残りのデータで学習を行なっていきます。
df_tokyo_month = df_tokyo.resample("M").mean()
y = df_tokyo_month["平均気温(℃)"]
train = y[:-12]
test = y[-12:]
sarima_model = sm.tsa.SARIMAX(train, order=(1,1,1),seasonal_order=(1,1,1,12))
result = sarima_model.fit()
result.summary()

sm.tsa.SARIMAXでSARIMAXモデルを実装できますが、説明変数Xを指定しなければSARIMAモデルとして使用できます。
引数orderには左からAR、I、MAのそれぞれの差分の値を指定します。引数seasonal_orderにはAR、I、MAに加え周期性として適応する値を指定します。今回の例では、日ごとのデータを月ごとに取り直したので12を指定しています。これらのパラメータを調整してAICが低くなるようなモデルを作成します。
最後に予測を行います。
bestPred = result.predict('2021-4-30', '2022-03-31')
plt.plot(df_tokyo_month["平均気温(℃)"])
plt.plot(bestPred, "red")
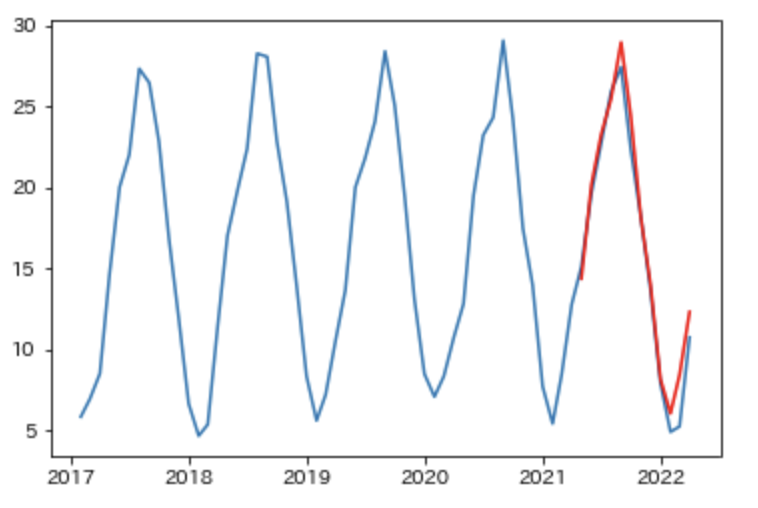
結果を見ると、おおよその予測はできていると考えていいと思います。パラメータをいじればもう少し精度が良くなるかもしれません。