主要ブラウザでCSSの三角関数がサポートされ、JavaScriptを使わずとも三角関数を用いた表現ができるようになりました。
筆者はド文系で、三角関数については学生時代に習ったはずの記憶もほとんど残っていませんでしたが、これを機に学習しました。
理解すると、なるほど便利だな!と感じたので、
CSSでの活用に必要な範囲で、数学に苦手意識のある方でも分かるようにまとめてみました。
よければご覧ください。
この記事を読んで分かること
- 三角関数を使うメリット
- 三角関数の基本的な考え方
- CSSプロパティの活用例
三角関数を使うメリット
先に、三角関数を使うことで得られるメリットを列挙します。
この後の定義の説明と合わせて、メリットの意味が理解いただけるかと思います。
-
比率の計算に利用できる
sinθ、cosθ、tanθは比を表したものですので、aspect-ratioなどの比率を扱うプロパティに活用できます。 -
円周上に要素を配置できる
sinθ、cosθで円周上の座標を取ることができるので、transformなどXY座標を扱うプロパティに活用できます。 -
繰り返しの表現や、波状に要素を配置できる
sinθ、cosθは角度ごとに周期的に値を返すため、波状の要素配置や、繰り返しのアニメーションなどに活用できます。
※CSSの三角関数は波形そのものの描画には向いていません。
あくまで要素を曲線上に要素をポツポツ置くことができる、という感じです(点描みたいなイメージ)
滑らかに描画しようとすると大量の要素が必要でとても効率が悪いので、
波形そのものを描きたい場合は、canvasやSVGを使う方が良いかと思います。
三角関数とは
直角三角形による定義

上図は、直角三角形の各辺を色分けしたものです。
角度θを基準として、
直角とつながる辺を隣辺、
もう一つの角とつながる辺を斜辺、
反対側にある辺を対辺といいます。
そして、角度θにおけるこれらの辺の組み合わせ(比)を
上図にあるとおり整理し、それぞれsinθ、cosθ、tanθと呼ぼう!ということにしたようです。
つまり、三角関数とは
「直角三角形のある角度と辺の関係性」を示したものです。
(厳密な定義ではないですが、ここでは分かりやすさを優先しています。)
単位円による定義

半径1の円に収まる直角三角形を考えます。
中心と円周上の点Pを結び、その線とx軸との角度θを基準に直角三角形を作ります。
前項の定義をふまえてこの直角三角形を見てみると、次のことが分かります。
- 斜辺(r)は円の半径そのものなので1である
- r=1を代入すると、上図の通りP点のx座標はcosθ、y座標はsinθとそれぞれ同じになる
つまり、三角関数を利用して円周上の座標を算出することができます。
単位円の直角三角形にはもう一つ特徴があります。
See the Pen CSS Trigonometric Functions: cos(), sin(), and tan() by web.dev (@web-dot-dev) on CodePen.
これはGoogleが三角関数の解説のために作成したcodepenです。
青いバーを動かしてみると分かりますが、
青い線(sinθ)も赤い線(cosθ)も、一周の間に半径と同じ長さになったり、長さが無くなったりしています。
先ほどの単位円として考えると、以下のとおり-1〜1の値を行き来しています。
cos(0deg)= 1
cos(90deg)= 0
cos(180deg)= -1
cos(270deg)= 0
cos(360deg)= 1
sin(0deg)= 0
sin(90deg)= 1
sin(180deg)= 0
sin(270deg)= -1
sin(360deg)= 0
つまり、一定間隔で値を反復する性質を持っています。
このため、角度の変化に合わせて軌跡を取ると以下図のように波を描きます。
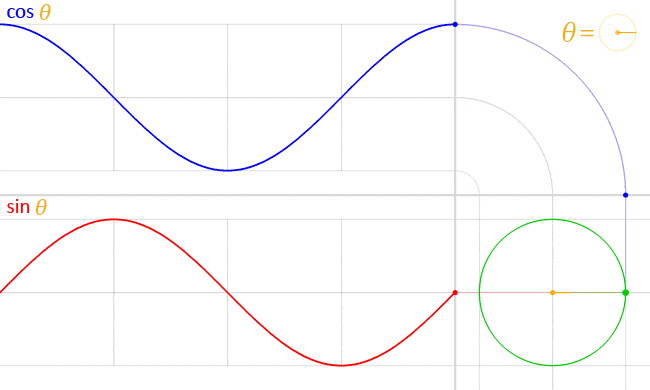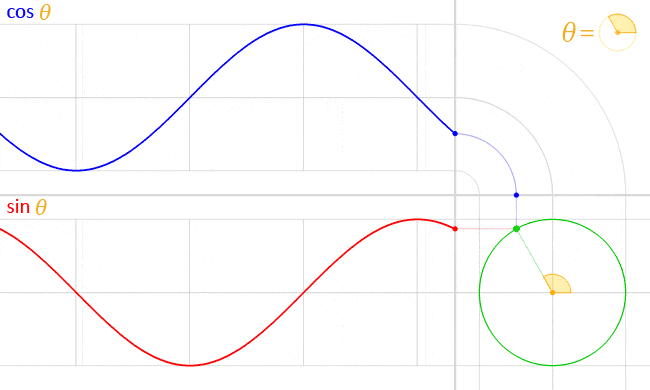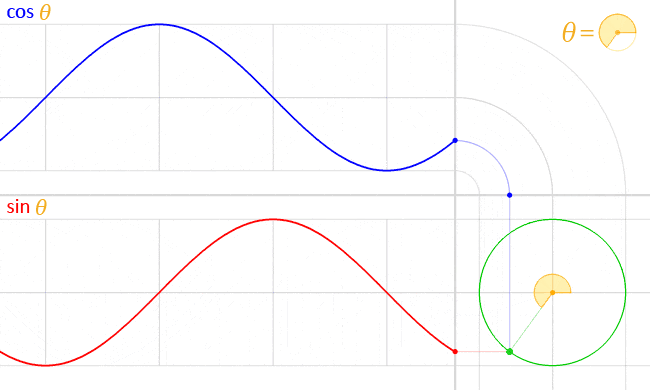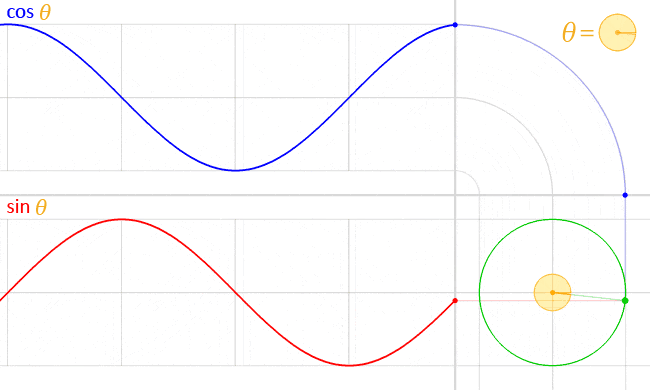
https://ja.wikipedia.org/wiki/三角関数
これらの性質を利用することで、先に述べた制作上のメリットを得ることができます。
CSSプロパティ
以下のプロパティが存在します。
sin()
cos()
tan()
asin()
acos()
atan()
atan2()
sin()、cos()、tan()の引数は角度(deg)またはラジアンです。
単位のない数値を入れるとラジアンとして扱われます。
ラジアン(弧度法)とは、円周の長さを基準とした角度の表現です。
度数法が円の1周を360°と定義するのに対して、ラジアンは2πと表現します。
細かい説明は省略しますが、角度以外の値でも三角関数を活用できるということです。
aがついているものは逆関数で、角度を算出します。(アークサインなどと読みます)
引数に2辺の比率を入れて、角度を求めることができます。
以下のような使い分けになります。
sin(),cos(),tan()→角度と1辺の長さが分かっている場合に、他の1辺の長さを求めたい場合
asin(),acos(),atan(),atan2()→2辺の長さが分かっている場合に、角度を求めたい場合
(アークサインなどについては私も使い所がまだ把握できていないため、この後の活用法では触れていません...)
caniuseは等しく90.4%で、本番環境で十分利用できる状況かと思います。
https://caniuse.com/?search=sin()
https://caniuse.com/?search=cos()
https://caniuse.com/?search=tan()
活用例
斜めの境界線
セクション間を斜めに区切るようなあしらいのデザイン、よくありますよね。
余白の調整が面倒でしたが、skew()とtanθの組み合わせで簡単に求められるようになりました。
codepenのサンプルを用意しました。
See the Pen 斜めの境界線 by atmosphere_lbk (@atmosphere_lbk) on CodePen.

上図では、skew()による要素の変形を示しています。
ちょっと分かりづらいのですが、変形前の領域をグレー、変形後の領域をピンクで示しています。
変形すると、高さX分、要素の中と外に食い込む部分が生じるため、余白を設定する必要があります。
transform-originが中心にあれば、skewで斜めになった辺(緑)は要素の幅aの中点を通ります。
つまり、skewの角度γに対する隣辺は、要素の幅aの1/2であることがわかります。
角度と隣辺がわかったので、tanθを利用して、上図のとおりXを求めることができます。
:root{
--angle:10deg;
--skew-padding: calc(tan(var(--angle)) * 100vw / 2);
}
~
.test-section2 {
position: relative;
width: 100vw;
height: fit-content;
padding: var(--skew-padding) 0;
*{
position: relative;
z-index: 1;
}
&::before{
content: '';
position: absolute;
inset: 0;
width: 100%;
transform: skewY(calc(-1 * var(--angle)));
}
}
参考記事
正三角形
正三角形は以下の考え方で、widthまたはheightの片方の値だけで求めることができます。

- 正三角形はどの内角も60°になる
- 三辺の長さが等しくなる(斜辺=width)
- cos(30deg) = 隣辺(height) / 斜辺(width)
- aspect-ratioはheight / widthなので、1/cos(30deg) で算出
- 向きはclip-path: polygon()で設定
.triangle {
background-color:#333;
width:60px;
aspect-ratio: 1/cos(30deg);
clip-path: polygon(50% 0,100% 100%,0 100%);
}
参考記事
円軌道を等間隔で周回
CSS変数と三角関数を組み合わせて、円軌道で周回する要素を作成できます。
こちらもcodepenのサンプルを用意しました。
See the Pen Untitled by atmosphere_lbk (@atmosphere_lbk) on CodePen.
角度のanimationを用意します。
@ propertyでCSS変数を定義して初期値0°とし、keyframesで360°まで変化させます。
/* カスタムプロパティを定義し、初期値0degにする */
@property --angle {
syntax: '<angle>';
initial-value: 0deg;/* 初期値 */
inherits: true;/* 親要素で値を上書きした場合、子要素にルールを継承する */
}
/* 角度のアニメーション */
@keyframes change-deg {
to {
--angle: 360deg;
}
}
.test-wrapper {
animation: change-deg linear 20s infinite paused;
animation-play-state: running;
--item-width: 20px;/* test-itemのwidth */
margin: 0 auto;
position: relative;
}
子要素(周回する円)ごとに角度設定用のCSS変数を付与します。
<!-- --item-count:test-itemの数 -->
<div class="test-wrapper" style="--item-count:6">
<span class="test-item" style="--item-index:0;"></span>
<span class="test-item" style="--item-index:1;"></span>
<span class="test-item" style="--item-index:2;"></span>
<span class="test-item" style="--item-index:3;"></span>
<span class="test-item" style="--item-index:4;"></span>
<span class="test-item" style="--item-index:5;"></span>
</div>
子要素ごとの角度を算出します。
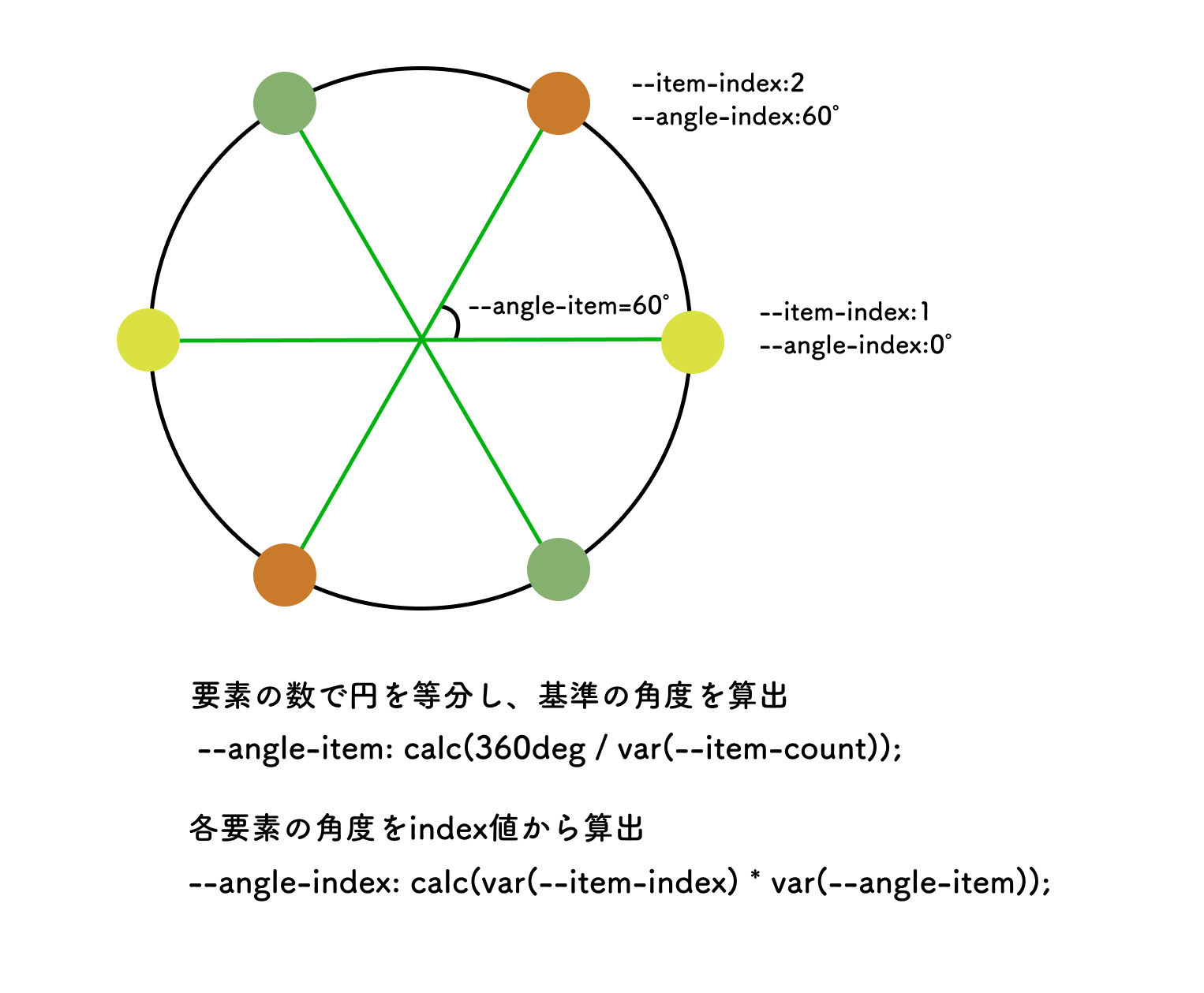
上図は角度の算出イメージです。
円の軌道上に要素を均等に配置するためには、
360°を要素の数で割った角度ごとに置けば良いということになります。
その基準角度を算出し、インデックス値を乗じることで要素ごとの角度を用意しています。
角度が求められたので、これを利用して座標を求めます。
前述のとおり、X座標=cosθ,Y座標=sinθなので、
位置を以下の通り算出します。
- X軸=cos(—angle+itemごとの角度)*半径
- Y軸=sin(—angle+itemごとの角度)*半径 -1
—angleは、前述のとおりanimationによって動的に360°まで変化しており、
これにより要素は等間隔のまま、円周上を移動します。
.test-item {
/* test-itemが周回する円軌道の半径 */
--radius: 100px;
/* 子要素の数で等分した角度 */
--angle-item: calc(360deg / var(--item-count));
/* 子要素ごとの角度 */
--angle-index: calc(var(--item-index) * var(--angle-item));
~
translate:
/* X軸=cos(keyframesで動的に変化する角度+itemごとの角度)*半径 */
calc(cos(var(--angle) + var(--angle-index)) * var(--radius))
/* Y軸=sin(keyframesで動的に変化する角度+itemごとの角度)*半径*-1 */
calc(sin(var(--angle) + var(--angle-index)) * var(--radius) * -1);
}
参考記事
波状の要素配置
他の方の作例ですが、最後に波状の配置を紹介します。
JHEYさんという方のcodepenです。
See the Pen Image Layout with CSS Trigonometric Functions ✨ [Tap to toggle] by Jhey (@jh3y) on CodePen.
こちらも前述の例と同様にCSS変数でindex値を用意していますね。
画像のY座標をsin()で算出していますが、角度を求める必要がないので、
sin()にindex値をそのまま入れ(ラジアンとして入力)、周期的な値を算出しているようです。
ul img {
--y: 0;
}
:checked ~ ul img {
--y: calc(sin(var(--index)) * 50%);
}
以上、CSSの三角関数について書きました。
CSSもどんどん進化していますね...
他の新機能もキャッチアップしていきたいです。
お読みいただきありがとうございました!
おすすめ記事
値の求め方がパターン化されています。
迷ったらこれを見に行くで良さそうです。
安定のICS MEDIAさん。ローディングアニメーションやメニューUIの活用例が載っています。