はじめに
これからの強化学習の2.5の内容をまとめた記事になります。
一言で言うと強化学習を並列計算しようという話。
どうやったらエージェント間でうまく情報をやりとりできるのかがテーマ。
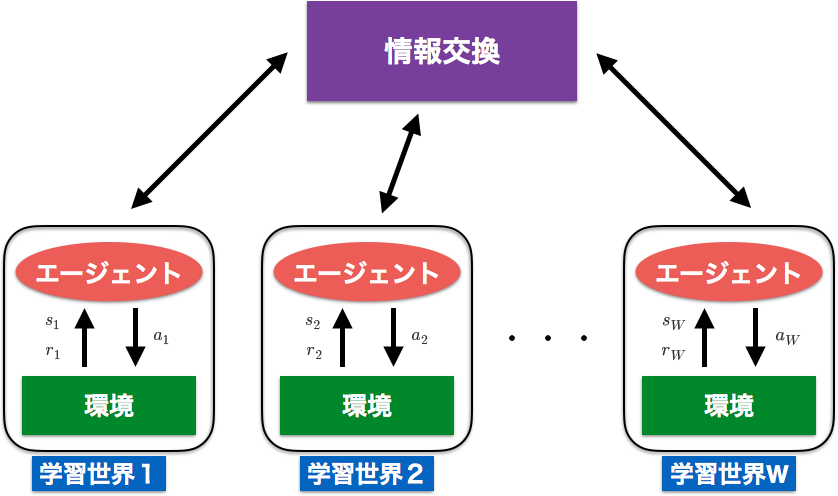
群強化学習の基本的な枠組み
Step0 エージェントと環境の組である学習世界を複数用意し、各学習世界の学習を初期化する
Step1 各学習世界が個別に、通常の強化学習法であらかじめ与えられたエピソード数だけ学習する
Step2 各学習世界の学習を何らかの方法で評価する
Step3 各学習世界の評価に基づいて、学習世界間で情報を交換することにより学習する
Step4 学習終了条件を満たせば終了し、そうでなければStep1へ戻る
- 通常の強化学習とは異なり、学習世界が複数ある。
- Step1ではそれぞれの学習世界で独立に強化学習を行い、決まったタイミングで情報の交換を行う。
- 学習方法はなんでもよいが、以下ではQ-Learningで学習することを考える
学習世界の評価方法
- Step2
- タスクごとに考えても良いが、汎用的なものを考える
- 各エピソードの割引報酬和$E$が汎用的で計算も軽いので、これを使う
E = \sum_{t=1}^{L}d^{L-t}r_t
$t$は時間
$d$は割引率
$L$は1エピソードの全行動回数
$r_t$は報酬
情報交換法
- Step3
- 交換するのは学習世界$i$のQ値のテーブルの値$Q_i(s,a)$
- 全学習世界の中で最も大きい割引報酬和$E$を獲得したQ値を$Q^{best}(s,a)$とする
最良値で更新
- 極めて単純だが、更新すると同じエージェントになるので、メリットも少ない。
Q_i(s,a) \leftarrow Q^{best}(s,a),(\forall s, a)
最良値との平均を取る
- エージェントに多様性をもたせたままにするには最も単純な方法
Q_i(s,a) \leftarrow \frac{Q^{best}(s,a) + Q_i(s,a)}{2},(\forall s, a)
Particle Swarm Optimization(PSO)
- 鳥の群れ行動にヒントを得て考案されたメタヒューリスティクスな方法
- 全世界の最良値と、各世界の最良値をともに考慮する
- 仮想的な速度を計算し、Q値を更新する
V_i(s,a) \leftarrow W_{pso}V_i(s,a) + C_1R_1(P_i(s,a) - Q_i(s,a)) + C_2R_2(G(s,a) - Q_i(s,a)),(\forall s,a)
\\
Q_i(s,a) \leftarrow Q_i(s,a) + V_i(s,a), (\forall s, a)
$P_i(s,a)$は各学習世界での最良値
$G(s,a)$は全世界での最良値
$W_{pso},C_1,C_2$は適当な重みパラメータ
$R_1,R_2$は0から1までの一様乱数
アントコロニー最適化
- アリの採餌行動にヒントを得て考案されたメタヒューリスティクスな方法
- 単純な行動ルールと、以下の示したフェロモンの仕組みで複雑な減少がモデリングできる
- アリの行動によって変化する
- 時間が経つと消える
- このフェロモンの要素をもたせたフェロモンQ値$Q_p(s,a)$を追加で用意し、全世界で共通に利用する
Q_p(s,a) \leftarrow (1 - \rho)Q_p(s,a) + \sum_{i=1}^{W} \frac{E_i}{\sum_{r=1}^WE_r} Q_i(s,a), (\forall s, a)
\\
Q_i(s,a) \leftarrow Q_p(s,a), (\forall s, a)
$\rho$はフェロモンの蒸発率
連続空間の場合
- Q値がルックアップテーブルの形で得られるのではなく、基底関数の線形結合として表現される
- 各学習世界は独立に学習を行うので、基底関数のパラメータが異なる場合がある（ガウシアンだと平均と分散）
- 学習世界間で基底関数が異なるとQ値の更新がやりにくい
- そこで各学習世界での基底関数のパラメータはそのままに、線形和の係数$v_k$のみを変更する
- あとは離散のときと同じ
Q(\bf p, \bf w_c) = \sum_{k = 1}^{N^C}v_kb_k\\
b_k = \frac{a_k}{\sum_{m = 1}^{N^C}a_m}\\
a_k = exp \left( -\frac{1}{2}(\bf p - \bf {\mu_k})^T \sum_k^{-1}(\bf p - \bf {\mu_k}) \right)\\
\Sigma_k = diag(\sigma_{k1}^2,\sigma_{k2}^2,...,\sigma_{k, M+N}^2)
$v_k$はk番目の基底関数の係数
$\mu_k$はk番目の基底関数の中心座標
$\sigma_k$はk番目の基底関数の分散
$N^C$は基底関数の個数
$\bf w_c = (v_k, \mu_k^T, \sigma_kn,N^C)(k = 1,2,...,N^C; n = 1,2,...M+N)$
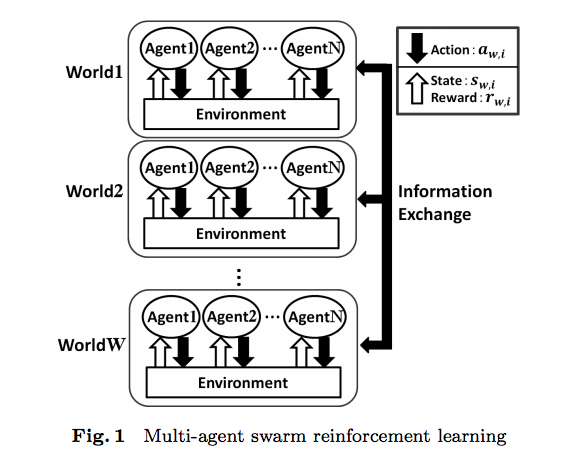
マルチエージェントの場合
- 一つの学習世界に複数のエージェントがいる場合を考える
- 各学習世界の汎用的な評価関数を見つけるのは困難
- 問題の種類ごとに評価関数を設計する
囚人のジレンマ
- 各エージェントの合理性と集団の合理性が対立する問題
- 協調行動は各エージェントにとっては損をすることが多く、学習が難しい
- そこで各学習世界の各エージェントがもつQ値$Q_{w,i}$に加えて、全世界の$i$番目のエージェントが共有する$Q_i^{common}$を導入する
- 協調行動が促進されるように、$Q_{w,i}$を$Q_i^{common}$で更新する
- 囚人のジレンマの問題設定では、裏切り行動をした時のほうが報酬が大きくなりやすく、協調行動ではむしろ報酬が小さくなると考えられる
- 協調行動はQ値が小さくなりがちだが、周りのエージェントが協調行動をしていた場合は下がらない
- まとめると「報酬が小さくなり」かつ「Q値が下がっていない」ときにQ値を更新すれば協調行動の学習が促進される
R_{w,i,t'} = \sum_{t=0}^{t'}\rho^{t'−t}r_{w,i,t}
\\
R_{w,i,t'−1} > R_{w,i,t'}\\
Q^{old}_{w,i}(s, a) < Q^{new}_{w,i}(s, a)
$\rho$は割引率
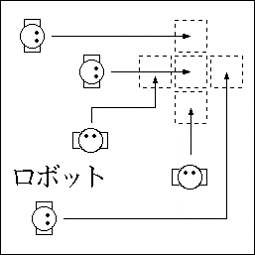
フォーメーション形成問題
- １つの部屋に複数のロボットがいて、各々目標位置に鎮座する問題
- 各ロボットは各学習世界で目標位置に移動するが、単純な割引報酬和では各世界の良さが表現できない
- ある学習世界のロボットたちが速やかに目標位置に鎮座したとき、その世界のロボットの行動回数およびその分散は小さいはずである
- そこで学習世界の良さは「ロボットの行動回数」「行動回数の分散」で表現する
http://vega.is.kit.ac.jp/work6.html