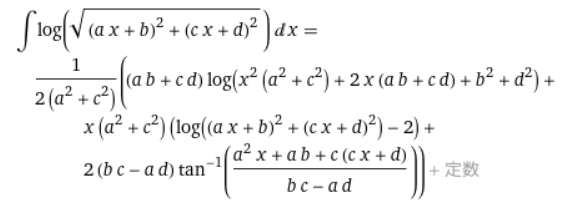0. 境界要素法の基礎
境界要素法(BEM)は有限差分法(FDM)・有限要素法(FEM)に並んでメジャーな解析手法である。
境界要素法の手法に関してはネット上にいくつか転がっているが、今回、自分のためにも定式化の流れをまとめたくなった。
この記事では、昔書いた有限差分法・有限要素法の記事と同様にポアソン方程式を対象とする。
ラプラス方程式でもよかったが、簡単にググったところ意外とポアソン方程式の例がなかったのでせっかくなのでこっちにした。
境界要素法は有限差分法と比較して数学的操作が結構面倒だ。
この記事ではその面倒な定式化の部分を境界要素法のまとめようと思う。
本当はプログラムの実装まで含めて一つの記事にしたかったのだが、Advent Calendar 2022に間に合わなかった…。
1. 数学的準備
あまり見慣れない公式や関数が出てくるので、先にそちらを解説しよう。
前提知識としては、$\nabla$の意味とガウスの発散定理がわかれば問題ないと思う。
1.1 多次元の部分積分法
部分積分については今さら説明するまでもないと思うが、導出からやってみよう。
まず、関数の積の微分は以下のように分解できる
\begin{align*}
(p(x) q(x))' = p'(x)q(x)+p(x)q'(x)
\end{align*}
この両辺を$[a,b]$の範囲で積分すると、
\begin{align}
\left[ p(x) q(x) \right]_a^b = \int_a^b \left( p'(x)q(x)+p(x)q'(x) \right)dx \tag{1}
\end{align}
となり、あとは並び変えると、
\begin{align*}
\int_{a}^{b} p'(x)q(x) dx = [p(x)q(x)]_a^b - \int_a^b p(x)q'(x) dx
\end{align*}
となる。簡単だ。
さて、この部分積分、一次元の関数ではなく高次元の場合に拡張するとどうなるだろうか。
ナブラの公式で、以下のようなものがある。
\begin{align*}
\nabla \cdot (p\boldsymbol{q}) = \nabla p \cdot \boldsymbol{q} + p\nabla\cdot \boldsymbol{q}
\end{align*}
次元は何次元でもいいのだが、理解しやすいように二次元か三次元としておこう。
これを領域$\Omega$で積分する。$\Omega$は任意1の領域だ。二次元なら円や三角形、三次元なら球や四面体などになる。
すると、
\begin{align*}
\int_\Omega \nabla \cdot (p\boldsymbol{q}) \, d\Omega = \int_\Omega \left(\nabla p \cdot \boldsymbol{q} + p\nabla\cdot \boldsymbol{q}\right) d\Omega
\end{align*}
ここで、左辺にガウスの発散定理を適用する。
\begin{align*}
\int_\Gamma (p\boldsymbol{q}) \cdot \boldsymbol{n} \, d\Gamma = \int_\Omega \left(\nabla p \cdot \boldsymbol{q} + p\nabla\cdot \boldsymbol{q}\right) d\Omega
\end{align*}
この時、$\Gamma$は$\Omega$の境界、例えば二次元の円なら円周、三次元の球なら表面を意味する。
$\boldsymbol{n}$はその境界の外側に向かう単位法線ベクトルだ。
これを並び変えると、
\begin{align}
\int_\Omega \nabla p \cdot \boldsymbol{q} d\Omega =
\int_\Gamma (p\boldsymbol{q}) \cdot \boldsymbol{n} \, d\Gamma - \int_\Omega p\nabla\cdot \boldsymbol{q} d\Omega \tag{2}
\end{align}
となる。
また、文字を$p=q$と$\boldsymbol{q}=\boldsymbol{p}$と入れ替えて並び変えると、
\begin{align}
\int_\Omega (\nabla\cdot \boldsymbol{p})q d\Omega =
\int_\Gamma (\boldsymbol{p}q) \cdot \boldsymbol{n} \, d\Gamma - \int_\Omega \boldsymbol{p}\cdot\nabla q d\Omega \tag{3}
\end{align}
という式も得られる。
この二つが高次元の部分積分である。右辺第1項が部分的に積分した項だ。
……え? 積分できてないだろって? いやいや、領域全体の積分を境界のみにしたのだから、積分したといえるだろう。
……納得できないかもしれないが、境界要素法にはこの公式が必須なので、覚えておこう。
1.2 デルタ関数
わかるようでわからない、デルタ関数の解説もしておこう。
デルタ関数$\delta(x)$は以下のように定義される超関数2だ。
\begin{align}
\delta(x) = \left\{ \begin{matrix} \infty & (x=0) \\ 0 & (x\neq 0) \end{matrix}\right. \tag{4}
\end{align}
さらにデルタ関数は次の積分を満たすように定義される。
\begin{align*}
\int_{-\infty}^{\infty}f(x)\delta(x) dx = \int_{a}^{b}f(x)\delta(x) dx= f(0)
\end{align*}
ただし、ここで$a<0<b$である。つまり、積分区間に0が含まれていることが条件だ。
デルタ関数についてはこれがすべてと考えてもらっていい。
この定義から、$\delta(x-\xi)$とすると、
\begin{align*}
\int_{-\infty}^{\infty}f(x)\delta(x-\xi) dx = \int_{a}^{b}f(x)\delta(x-\xi) dx= f(\xi)
\end{align*}
がえられる。このときは、$a<\xi<b$である。つまり積分区間に$\xi$が含まれていることが条件といえる。
これは変数変換を使えば簡単に証明できる。
次に、デルタ関数を多次元に拡張しよう。といっても、これも難しくない。
\begin{align}
\delta(x,y) = \left\{ \begin{matrix} \infty & (x=0 \land y=0) \\ 0 & (x\neq 0 \lor y\neq 0) \end{matrix}\right. \tag{5}
\end{align}
$\land$は"かつ"、$\lor$は"または"を意味する。
つまり、$x=0$かつ$y=0$の時だけ無限大で、そのほかは0となる超関数だ。
そして、積分のほうも同様である。
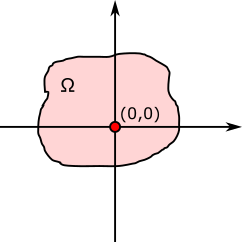
\begin{align*}
\int_\Omega f(x,y)\delta(x,y) d\Omega = f(0,0)
\end{align*}
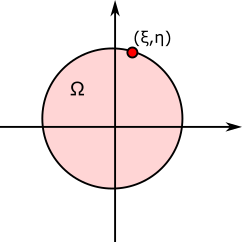
下図のように$\Omega$は$(0,0)$を含む任意の領域だ。もちろん、一次元と同様に無限に大きい領域でもよい。
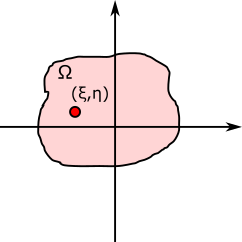
同様に、$f(x-\xi, y-\eta)$のとき、
\begin{align*}
\int_{\Omega}f(x,y)\delta(x-\xi,y-\eta) d\Omega = f(\xi,\eta)
\end{align*}
となる。$\Omega$の条件は$(\xi,\eta)$を含む領域である。
……すこし話がそれるが、$f(x,y)$はベクトル表記を用いて$f(\boldsymbol{x})$と表すことが多い。
$\boldsymbol{x}=(x,y)$,$\boldsymbol{\xi}=(\xi, \eta)$とすると、上式は次のように表せる。
\begin{align}
\int_{\Omega}f(\boldsymbol{x})\delta(\boldsymbol{x}-\boldsymbol{\xi}) d\Omega = f(\boldsymbol{\xi}) \tag{6-A}
\end{align}
今後もこの表現で解説するので慣れておこう。
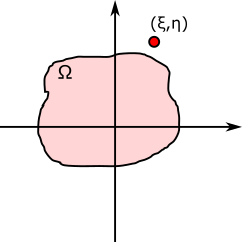
さて、上式において$\boldsymbol{\xi}$が領域$\Omega$の外側のとき、当然、その答えは0となる。
なぜなら、$\delta(\boldsymbol{x})$が0だからだ。
\begin{align}
\int_{\Omega}f(\boldsymbol{x})\delta(\boldsymbol{x}-\boldsymbol{\xi}) d\Omega = 0 \tag{6-B}
\end{align}
それでは、$\boldsymbol{\xi}$が境界上だったらどうなるだろうか。その答えは単純で次のようになる。
\begin{align}
\int_{\Omega}f(\boldsymbol{x})\delta(\boldsymbol{x}-\boldsymbol{\xi}) d\Omega = cf(\boldsymbol{\xi}) \tag{6-C}
\end{align}
この右辺の$c$は滑らかな境界上なら$1/2$になる。
滑らかというのは簡単に言えば曲線や直線のこと、要は角ばってないということだ。領域外なら0, 領域内なら$f(\boldsymbol{\xi})$だから、境界上は$\frac{1}{2}f(\boldsymbol{\xi})$となるというのは直観的な気がする。
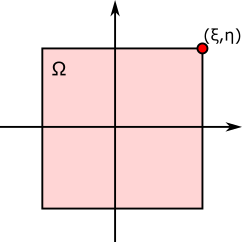
つぎに滑らかではない場所は、角の角度で計算できる。
例えば、$\Omega$を長方形として、その頂点ならば、内角は90°である。
ここから、$c=90/360=1/4$と計算する。これもまた直観的だ。
$\boldsymbol{\xi}$が$\Omega$の外側なら$c=0$、$\boldsymbol{\xi}$が$\Omega$の内側なら$c=1$とすれば、式(6-A)-(6-C)はまとめるて次のように表すことができる。
\begin{align}
\int_{\Omega}f(\boldsymbol{x})\delta(\boldsymbol{x}-\boldsymbol{\xi}) d\Omega = cf(\boldsymbol{\xi}) \tag{6}
\end{align}
境界要素法ではこの式をそのまま使うので、覚えておこう。
2. 境界要素法
定式化する前に、境界要素法の特徴を説明をしていこう。
有限差分法や有限要素法と違って、境界要素法は境界のみを分割する手法だ。
よって、格子数がほかの手法と比較してとても少なくなる。これは計算時間やメモリの観点からいうとメリットに思える。
しかし、境界要素法は有限差分法・有限要素法と違って、連立方程式が密になるので、どちらが高速かといわれると難しい。
また、有限差分法や有限要素法は格子点上の値を求める手法だったが、境界要素法は関数をそのまま求める手法である。これもほかの手法にはない特徴だといえる。
それでは、そんな癖のある手法である境界要素法を定式化していこう。
2.1 問題設定
今回も簡単のため、$u(\boldsymbol{x})=u$が未知の関数、$f(\boldsymbol{x})=f$が既知の関数とした、以下の二次元ポアソン方程式を考える。
\begin{align*}
\nabla \cdot \nabla u = f \ \ (\text{in }\Omega)
\end{align*}
また、$\Omega$は計算領域を表す。
多くの記事では一部をノイマン境界条件、一部をディリクレ境界条件として同時に説明することが多いのだが、わかりやすくするために、以下のようなディリクレ境界条件のみの場合を考えよう。
ノイマン境界条件についての拡張ものちに話すので安心してほしい。
\begin{align}
u = U\ \ (\text{in }\Gamma)
\end{align}
ここで、$\Gamma$は$\Omega$の境界である。
2.2 境界積分方程式の導出
まず、ポアソン方程式の両辺に$u^* (\boldsymbol{x})=u^*$という関数をかける。この$u^*$は後々ちゃんと定義するので、とりあえず今は何らかの関数ということだけ認識しておこう。
\begin{align*}
\nabla \cdot (\nabla u) u^*= fu^* \ \ (\text{in }\Omega)
\end{align*}
さらに、これを領域$\Omega$で積分する。
\begin{align*}
\int_\Omega \nabla \cdot (\nabla u) u^* \,d\Omega = \int_\Omega f u^* \,d\Omega \ \ (\text{on }\Gamma)
\end{align*}
そしてここで、先ほどの多次元の部分積分を使う。
式(3)の$p=\nabla u$, $\boldsymbol{q}=^*$とすると、次のように変形できる。
\begin{align*}
\int_\Gamma (\nabla u)u^* \cdot \boldsymbol{n} d\Gamma - \int_\Omega \nabla u\cdot \nabla u^* \,d\Omega= \int_\Omega fu^*\, d\Omega
\end{align*}
さらに、この第二項をもう一回部分積分する。
式(2)の$p=u$, $\boldsymbol{q}=\nabla u^*$とすると、次のように変形できる。
\begin{align*}
\int_\Gamma (\nabla u)u^* \cdot \boldsymbol{n} d\Gamma - \int_\Gamma u\nabla u^* \cdot \boldsymbol{n} d\Gamma + \int_\Omega u\nabla \cdot \nabla u^*d\Omega= \int_\Omega f u^*\, d\Omega
\end{align*}
2.3 グリーン関数の導入
ここで、一旦放置していた$u^*$を次のように定義しよう。
\begin{align}
\nabla \cdot \nabla u^* = \delta(\boldsymbol{x}-\boldsymbol{\xi}) \tag{7}
\end{align}
すると、先ほどの式は次のように変形できる。
\begin{align*}
\int_\Gamma (\nabla u)u^* \cdot \boldsymbol{n} d\Gamma - \int_\Gamma u\nabla u^* \cdot \boldsymbol{n} d\Gamma + \int_\Omega u\delta(\boldsymbol{x}-\boldsymbol{\xi})d\Omega= \int_\Omega f u^*\, d\Omega
\end{align*}
この左辺第3項はデルタ関数の項で話した式(6)から、
\begin{align*}
\int_\Gamma (\nabla u)u^* \cdot \boldsymbol{n} d\Gamma - \int_\Gamma u\nabla u^* \cdot \boldsymbol{n} d\Gamma + cu(\boldsymbol{\xi})= \int_\Omega f u^*\, d\Omega
\end{align*}
と表せる。
最後にこれを並び変えると、
\begin{align}
cu(\boldsymbol{\xi})= \int_\Gamma u\nabla u^* \cdot \boldsymbol{n} d\Gamma -\int_\Gamma (\nabla u)u^* \cdot \boldsymbol{n} d\Gamma+\int_\Omega f u^*\, d\Omega \tag{8}
\end{align}
という式が得られる。
ここで一旦整理しよう。
左辺が$\boldsymbol{x}$から$\boldsymbol{\xi}$になったのでちょっと混乱したかもしれないが、$\boldsymbol{\xi}$を変数とみなして、右辺を何とかして求めることができれば、$u$という関数がどういう形をしているのかがわかる。
今のところ上の中で既知のものは、第一項の$u$と第三項の$f$のみだ。第一項の$u$は境界上のみで、ディリクレ境界条件で定義されている。
手がかりを増やすためにも、次は$u^*$について考えよう。
$u^*$は式(7)のように定義されており、このような関数はグリーン関数という名前がある。
実はこのグリーン関数がどんな形をしているかは偉大な先人たちが計算してくれている。
ここで導出まで書くと少し冗長になるので省略する。今回はありがたくそのまま使わせていただくことにしよう3。
二次元の場合、$u^*$は以下のような関数になる。
\begin{align}
u^* = \frac{1}{2\pi}\ln |\boldsymbol{x}-\boldsymbol{\xi}| \tag{9}
\end{align}
これで$u^*$の具体的な形がわかったため、$\nabla u^*$も簡単に計算できる。
つまり、式(8)の第一項と第三項が計算できることになる。
あとは$\nabla u$さえわかれば、$u$の形が分かることになるのだ! ゴールが見えてきた!
2.4 境界積分方程式の離散化
前述の通り、境界要素法は計算領域の境界を離散化する手法であり、離散化によりこの境界上の$\nabla u$を求める。
まず、式(8)の右辺を全部左にもってこよう。
\begin{align}
cu(\boldsymbol{\xi}) - \int_\Gamma u\nabla u^* \cdot \boldsymbol{n} d\Gamma + \int_\Gamma (\nabla u)u^* \cdot \boldsymbol{n} d\Gamma - \int_\Omega f u^*\, d\Omega = 0 \tag{10}
\end{align}
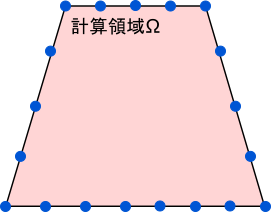
そして図のように$\Gamma$を$\Gamma_1, \cdots, \Gamma_N$と分割する。
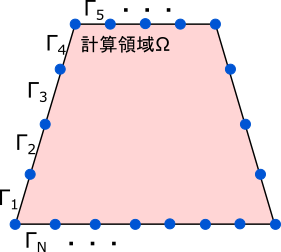
すると、それぞれの積分は次のように分割した境界上の積分の和に分解できる。
\begin{align}
cu(\boldsymbol{\xi}) - \sum_{i=1}^N \int_{\Gamma_i} u\nabla u^* \cdot \boldsymbol{n} d\Gamma + \sum_{i=1}^N \int_{\Gamma_i} (\nabla u)u^* \cdot \boldsymbol{n} d\Gamma - \int_\Omega f u^*\, d\Omega = 0 \tag{11}
\end{align}
この時、各$\Gamma_1,\cdots,\Gamma_N$の中心を代表点として、その座標を$\boldsymbol{x}_1,\cdots\boldsymbol{x}_N$としよう。
ここで、$u\approx p$, $\nabla u\cdot\boldsymbol{n}\approx q$という関数であると近似をする。
$p$と$q$は各$\Gamma_i$に渡って一定であり、その値は$p_i$, $q_i$とする。
すると、上式はさらに次のように変形できる。
\begin{align*}
cu(\boldsymbol{\xi}) - \sum_{i=1}^N \int_{\Gamma_i} p_i\nabla u^* \cdot \boldsymbol{n} d\Gamma + \sum_{i=1}^N \int_{\Gamma_i} q_iu^* d\Gamma - \int_\Omega f u^*\, d\Omega &= 0 \\
\iff cu(\boldsymbol{\xi}) - \sum_{i=1}^N p_i \int_{\Gamma_i} \nabla u^* \cdot \boldsymbol{n} d\Gamma + \sum_{i=1}^N q_i \int_{\Gamma_i} u^* d\Gamma - \int_\Omega f u^*\, d\Omega &= 0
\end{align*}
つぎに、$u^*=p^*$, $\nabla u^*\cdot\boldsymbol{n}=q^*$とする。こちらは近似ではなく単純にわかりやすいように文字を置き換えただけだ。
$p^*$と$q^*$はどちらも$\boldsymbol{x}$と$\boldsymbol{\xi}$の関数である。
そこで、$\boldsymbol{\xi}=\boldsymbol{x}_j$のとき、それぞれ$p_j^*$, $q_j^*$とする。
これを使って、上式をさらに書き換えよう。ついでに、第一項も$u(\xi)=p_j$と置き換えておく。すると、
\begin{align*}
\iff cp_j - \sum_{i=1}^N p_i \int_{\Gamma_i} q_j^* d\Gamma + \sum_{i=1}^N q_i \int_{\Gamma_i} p_j^* d\Gamma - \int_\Omega f u^*\, d\Omega &= 0
\end{align*}
となる。
さらに、見やすくするために、以下のように$P_{i,j}^*$, $Q_{i,j}^*$を定義する。
\begin{align*}
P_{i,j}^* &= \int_{\Gamma_i} p_j^* d\Gamma \\
Q_{i,j}^* &= \int_{\Gamma_i} q_j^* d\Gamma
\end{align*}
すると、次のようになる。
\begin{align}
\iff c_jp_j - \sum_{i=1}^N p_i Q_{i,j}^* + \sum_{i=1}^N q_i P_{i,j}^* - \int_\Omega f u^*\, d\Omega &= 0 \tag{12}
\end{align}
よし、これで、$j=1,\cdots,N$とすれば連立方程式にできる!!
少し混乱してるかもしれないので、整理しよう。
- $p_i=u(\boldsymbol{}\boldsymbol{x_i})$: 既知の値。ディリクレ境界条件で与えられている。
- $q_i=\nabla u \cdot \boldsymbol{n}(\boldsymbol{x_i})$: 未知数。
- $\displaystyle P_{i,j}^*=\int_{\Gamma_i} u^*(\boldsymbol{\xi}=\boldsymbol{x_j}) d\Gamma$: $x$に関する既知の関数の積分値。式(9)から計算できる。
- $\displaystyle Q_{i,j}^*=\int_{\Gamma_i} \nabla u^*\cdot \boldsymbol{n}(\boldsymbol{\xi}=\boldsymbol{x_j}) d\Gamma$: $x$に関する既知の関数の積分値。式(9)から計算できる。
- $\displaystyle \int_\Omega f u^*, d\Omega$: 既知の関数$f$と既知の関数$u^*$の積の積分値
つまり、式(12)は$q_i$に関する連立方程式なのだ。連立方程式っぽく書き換えよう。
\begin{align*}
\begin{cases}
P_{1,1}^* q_1 + P_{2,1}^* q_2 + \cdots +P_{N,1}^* q_N &= -c_1p_1 + \sum_{i=1}^N p_i Q_{i,1}^* + \int_\Omega f u^*\, d\Omega \\
P_{1,2}^* q_1 + P_{2,2}^* q_2 + \cdots +P_{N,2}^* q_N &= -c_2p_2 + \sum_{i=1}^N p_i Q_{i,2}^* + \int_\Omega f u^*\, d\Omega \\
& \vdots\\
P_{1,N}^* q_1 + P_{2,N}^* q_2 + \cdots +P_{N,N}^* q_N &= -c_Np_N + \sum_{i=1}^N p_i Q_{i,N}^* + \int_\Omega f u^*\, d\Omega
\end{cases}
\end{align*}
この連立方程式を解けば、めでたく$q_i=\nabla u(\boldsymbol{x}_i)\cdot \boldsymbol{n}$の値が解けたことになる。
あとは、式(8)に代入すれば全領域の$u$の値を求めることができる。
それでは、先延ばしにしていたノイマン境界条件の場合はどうすればいいだろうか。
これは特に難しいことじゃない。上記はディリクレ境界条件だから$p_i$が既知で$q_i$が未知だった。
ノイマン境界条件は単純に$q_i$が既知で$p_i$が既知になるだけだ。
同様に、境界の一部がディリクレ境界条件、一部がノイマン境界条件の場合は、ディリクレ境界条件が与えられている場所は$p_i$を既知、ノイマン境界条件が与えられている場所は$q_i$を既知として連立方程式を立てればいいだけである。
2.5 積分の計算
上記の$P_{i,j}^*$, $Q_{i,j}^*$, そして$\int_\Omega fu^*d\Omega$はそれぞれ実際に計算する必要がある。
この積分は解析的に求めることができない場合もあり、その場合は数値積分が必須になる。
実際に$P_{i,j}^*$を計算してみよう。
\begin{align*}
P_{i,j}^* = \int_{\Gamma_i}p_j^*\,d\Gamma= \int_{\Gamma_i} \frac{1}{2\pi}\ln |\boldsymbol{x}-\boldsymbol{x}_j| d\Gamma = \frac{1}{2\pi} \int_{\Gamma_i}\ln \sqrt{(x-x_j)^2 + (y-y_j)^2} d\Gamma
\end{align*}
ここで、$\Gamma_i$は$(x_i, y_i)$から$(x_{i+1}, y_{i+1})$までの直線としよう。
もちろん、境界が曲線の場合は曲線で計算するほういいと思うが、計算の都合上、直線として計算することも多い。
分割数を増やしていけば曲線による影響を徐々に無視できるようになるからだ。
ということで、直線で線積分する。線積分の計算法は忘れやすいので実際にやっていこう。
$(x_i, y_i)$から$(x_{i+1}, y_{i+1})$までの経路は次のように表せる。
\begin{align*}
\left(
\begin{matrix}
x \\
y
\end{matrix}
\right) = \left(
\begin{matrix}
x_i + (x_{i+1}-x_i)t \\
y_i + (y_{i+1}-y_i)t
\end{matrix}
\right)
= \left(
\begin{matrix}
x_i + t\Delta x_i \\
y_i + t\Delta y_i
\end{matrix}
\right) \ \ (0\leq t\leq 1)
\end{align*}
ここで、$\Delta x_i=x_{i+1}-x_i$, $\Delta y_i=y_{i+1}-y_i$である。
そして、これを$t$で微分すると、
\begin{align*}
\frac{d}{dt}\left(
\begin{matrix}
x \\
y
\end{matrix}
\right)
= \left(
\begin{matrix}
\Delta x_i \\
\Delta y_i
\end{matrix}
\right)
\end{align*}
となる。
よって、元の線積分は次のように変換できる。
\begin{align*}
\frac{1}{2\pi} \int_{\Gamma_i}\ln \sqrt{(x-x_j)^2 + (y-y_j)^2} d\Gamma &=
\frac{1}{2\pi} \int_0^1 \ln\sqrt{(t\Delta x_i+x_i-x_j)^2+(t\Delta y_i+y_i-y_j)^2} \left|\begin{matrix}
\Delta x_i \\
\Delta y_i
\end{matrix}\right|dt \\
&=\frac{1}{2\pi} \sqrt{(\Delta x_i^2+\Delta y_i^2)} \int_0^1 \ln\sqrt{(t\Delta x_i+x_i-x_j)^2+(t\Delta y_i+y_i-y_j)^2} dt
\end{align*}
あとは積分計算するだけ…だが、あまりにも面倒なので、Wolfram Alphaで計算した。
$\Delta x_i=a$, $x_i-x_j=b$, $\Delta y_i=c$, $y_i-y_j=d$として計算を投げると次のようになった。
同様にして、$Q_{i,j}^*$も頑張れば計算できる。
ただ、複雑な式になることが目に見えているので、今回は省略する。
このように、計算結果はかなり複雑になる。
プログラムにするときはそのまま打ち込めば問題ない……とはいえ、めんどうなら、数値積分した法がいいと思う。
数値積分のモジュールはたくさんあるし、格子分割を細かくしてしまえば、数値積分のほうも精度が高くなっていくからだ。
3. まとめ
この記事では境界要素法の定式化について解説してきた。
二次元ポアソン方程式の場合、最終的な流れは次の通りだ。
まず、以下の連立方程式を解く。
\begin{align*}
\begin{cases}
P_{0,0}^* q_0 + P_{1,0}^* q_1 + \cdots +P_{N,0}^* q_N &= -c_0p_0 + \sum_{i=0}^N p_i Q_{i,0}^* + \int_\Omega f u^*\, d\Omega \\
P_{0,1}^* q_0 + P_{1,1}^* q_1 + \cdots +P_{N,1}^* q_N &= -c_1p_1 + \sum_{i=0}^N p_i Q_{i,1}^* + \int_\Omega f u^*\, d\Omega \\
& \vdots\\
P_{0,N}^* q_0 + P_{1,N}^* q_1 + \cdots +P_{N,N}^* q_N &= -c_1p_N + \sum_{i=0}^N p_i Q_{i,N}^* + \int_\Omega f u^*\, d\Omega
\end{cases}
\end{align*}
ここで、それぞれの文字の定義は次のようになっている。
- $p_i=u(\boldsymbol{}\boldsymbol{x_i})$: ディリクレ境界条件で与えられている場合、既知の値。違う場合未知数
- $q_i=\nabla u \cdot \boldsymbol{n}(\boldsymbol{x_i})$: ノイマン境界条件で与えられている場合、既知の値。違う場合未知数
- $\displaystyle P_{i,j}^*=\int_{\Gamma_i} u^*(\boldsymbol{\xi}=\boldsymbol{x_j}) d\Gamma$: $x$に関する既知の関数の積分値。式(9)から計算できる。
- $\displaystyle Q_{i,j}^*=\int_{\Gamma_i} \nabla u^*\cdot \boldsymbol{n}(\boldsymbol{\xi}=\boldsymbol{x_j}) d\Gamma$: $x$に関する既知の関数の積分値。式(9)から計算できる。
- $\displaystyle \int_\Omega f u^*, d\Omega$: 既知の関数$f$と既知の関数$u^*$の積の積分値
そして、$u^*$は次のような関数である。
\begin{align*}
u^* = \frac{1}{2\pi}\ln |\boldsymbol{x}-\boldsymbol{\xi}|
\end{align*}
これを用いて、すべての$p_i=u(\boldsymbol{}\boldsymbol{x_i})$, $q_i=\nabla u \cdot \boldsymbol{n}(\boldsymbol{x_i})$を求めれば、
\begin{align*}
cu(\boldsymbol{\xi})= \int_\Gamma u\nabla u^* \cdot \boldsymbol{n} d\Gamma -\int_\Gamma (\nabla u)u^* \cdot \boldsymbol{n} d\Gamma+\int_\Omega f u^*\, d\Omega
\end{align*}
に代入して、計算領域全域の$u$を求めることができる。
今回は理論だけになってしまったが、近いうちに実装のほうも書いていきたい。