電場の数値解析：有限差分法(FDM) －実践編－

前書き

前回の『電場の数値解析：有限差分法(FDM)　－基礎編－』の続き。

今回はやっと数式だけでなく、pythonで有限差分法を書いていく。
それにしてもネット上にプログラムを書いていくのは、下手なのがバレそうでちょっと恥ずかしい。
特に、pythonはスクリプトの綺麗さがそのまま高速化・最適化につながっていたりするので、色々と突っ込まれそうだ……。

そういう意味で、C,C++やFortranなどはforループなどを脳筋に回しても高速になってくれて、最近はこっちのほうが好きになってきた。
……話がそれた。それでは数値解析を始めよう。

実際に作ったプログラムはまとめの項にgithubを載せているので、とりあえず一度動かしたい方はそちらをまずダウンロードして動かしてみて欲しい。

問題設定

最初からあらゆる問題を解けるようなプログラムを書くのは難しいので、まずは問題設定をしていこう。

ポアソン方程式
$$
\nabla \cdot \nabla u = f
$$
のソース項$f$は、0にしよう。

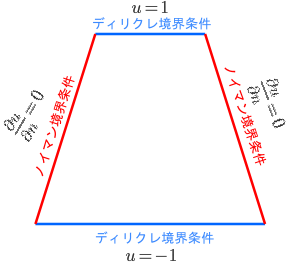
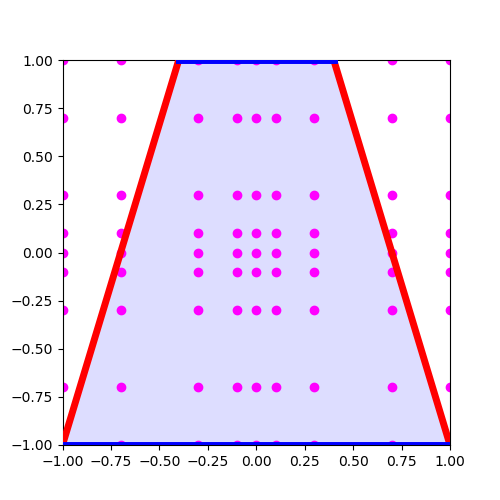
計算領域を次のような等脚台形と定義し、上と下の辺をディリクレ境界条件、左右をノイマン境界条件とし、以下のように設定する。

図1：計算領域

まとめて書こう。

\begin{align}
\nabla \cdot \nabla u &= 0 \ \ \text{(領域内)}\\
u &= 1 \ \ \text{(上辺)} \\
u &= -1 \ \ \text{(下辺)} \\
\frac{\partial u}{\partial n} &= 0 \ \ \text{(左右辺)}
\end{align}

この問題を解くプログラムを書いていこう。
……といっても、これだけを解くプログラムを書くというのもつまらないので、ある程度の一般性は考えながら実装していこう。

なお、今回使うライブラリはnumpyとmatplotlibのみとする。

実装

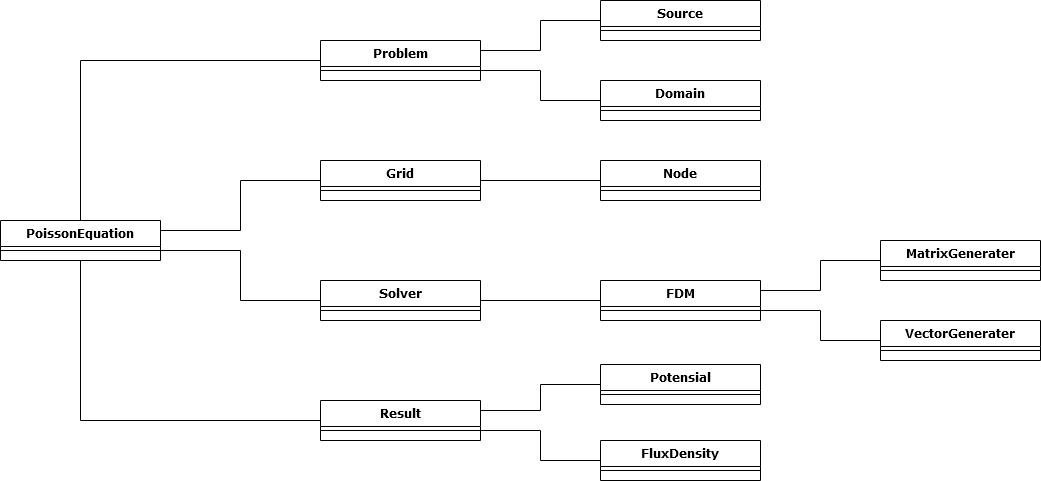
早速、プログラムを……と言う前に、まず、クラス図を簡単に書いてみよう。
クラス図と言っても、みんなで共有するわけではなく、自分の脳の整理のために書くものなので、ガチガチに書くわけではなく、こんなクラスがありそうだな～程度の適当な図で書いていいと思う(予防線)。

まず、FDM流れを確認しよう。

• Step 1: 問題設定 - 領域設定・ソース項設定
• Step 2: 格子分割
• Step 3: FDMで解く - 連立方程式の生成とそれを解く
• Step 4: 結果

愚直にこれら４つを大きなクラスとして分けてみた。

図2：クラス図

簡単に説明しておこう。
PoissonEquationクラスがいわゆるmainのものだ。
そして、Problemが問題設定で、領域Domainクラス・ソース項Sourceクラスの２つに分けた。
境界条件は分けても良いかもしれないが、Domainクラスに含めることにした。

次に、格子分割のクラスで、これはGridクラスに置いた。
Gridは格子点を取り扱うクラス(Node)でできている。
わざわざ、Nodeクラスを作ったのは、次回やろうと考えている、有限要素法という手法で利用する、各格子点を結ぶ線分(Edge)や、区域(Cell)などを取り扱おうと考えていたからだ。

その次の、Solverクラスもその下にFDMを置いているが、これもFEM等他の手法を下に置くためだ。
線では明示されていないが、子クラスとかにすべき？(正直まだ作ってないからわかってない)

最後に、結果(Result)は電位(Potential))と、電場(FluxDensity)に分けた。

よし、方向性は立ったし、プログラムを書いていこう！
ただ、作ってるうちにちょっとずつ変わる可能性が高い。

ところで、筆者はクラスの末端の方から細かく書いていくタイプなのだが、これは一般的なのだろうか……？　いい加減、「プログラムの王道な書き方」のような本を読んだほうが良い気がする。
まあ今回は自分のやり方の通り進めていくことにするので、変なやり方だったらごめん。

Step 1：問題設定

まず、問題を設定をプログラム上でしていこう。
このときに最初に考えるのは、どのようにデータとして保存しておくかということだ。

領域設定(Domainクラス)

例えば、上記の等脚台形の問題だけに対応すると考えたとき、「下辺の長さ」「上辺の長さ」「高さ」さえあれば形状を一意に決められるわけだから、データとしては十分だ。
ただこのようなデータにしてしまうと、等脚台形、長方形(上辺＝下辺)、正方形(上辺＝下辺＝高さ)あたりは実現できるが、その他のあらゆる形状には対応できず、一般性がなく面白みもない。
逆に一般性を求めすぎるにも難があり、すべての頂点、曲線を有限個のデータ数で表現するのはまず不可能だ。関数を渡すなどすればできるかもしれないが、プログラムがかなり複雑化してしまうのは目に見えている。
このように、一般性を求めるとプログラムが複雑になり、逆にプログラムを簡単にしようとすると一般性が損なわれる傾向にある(ただの筆者の経験則であり、異論は認める)。

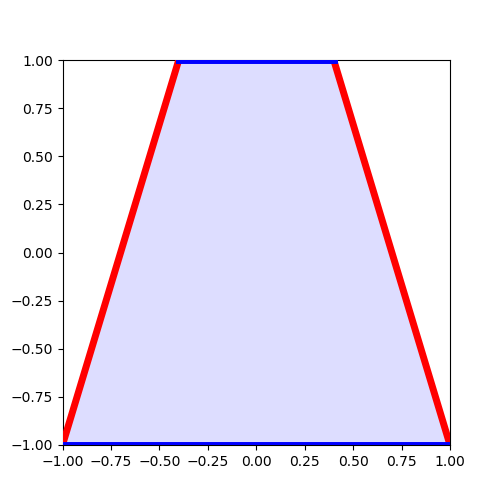
今回は、「多角形の頂点の座標」を配列として保持することとしよう。
こうすれば、あらゆる多角形に対応できてある程度の一般性も保持できるし、データとしても簡単そうだ。
円などには対応できないが……、まあここは正20角形とかにすればある程度近似できるし、必要なときに拡張していけばいいだろう。
ソースは以下のようにした。

domain.py

import numpy as np
import matplotlib.pyplot as plt

class Domain(object):
    def __init__(self, shape, bc):
        self.shape=shape
        self.bc = bc

class Polygon(Domain):
    def __init__(self, vertexes, bc, priority=None):
        super().__init__("Polygon", bc)
        self.nVertexes=len(vertexes)
        self.vertexes = np.array(vertexes)  # 引数のvertexesがリストだった場合、np.arrayに置き直す。

わざわざDomainクラスを作り、子クラスとしてPolygonクラスにしたのは、今後のもしかしたら、円に対応できるよう、Circleクラスを作るなどする可能性があるからだ。
逆に、長方形(Rectangle)クラスを作って高速に処理…なども考えられる。
まあとにかく、拡張性を考慮してこのようにした。
なお、筆者はプロなどではなく、素人なので、これが正しいと言い切っているわけではない(予防線)。自分なりのコードを作るのが良いと思う。

上記のコードを見るとわかるが、持っているデータは親クラスにshape, bc、小クラスにnVertexes, vertexesを持っている。
変数名とコードでなんとなくわかると思うが、一応以下のように定義している。

• shape: 利用する領域の形状の名前。shape = "Polygon"
• bc: 境界条件
• nVertexes: Polygonの頂点の数
• vertexes: 頂点の座標。vertexes[0]から順に結んでいけば、多角形ができる。

ところで、境界条件はどのように表現しようか。
今回は、次のような辞書型で表現することにする。

bc = {"bc":[{"bctype":"Dirichlet"または"Neumann" , "constant":定数}, ...], "priority":[...]}

この、"constant"に境界条件右辺の定数を、"bctype"にディリクレ／ノイマン境界条件を指定する。
"bc"は、"constant"と"bctype"のリストとして作っている。bc["bctype"][0]がvertexes[0]とvertexes[1]を結ぶ境界の境界条件…と言う意味だ。
みればわかると思うが、定数しか対応していない……、これはただ面倒だっだ。関数型を引数に渡すなどすれば定数以外も簡単に実現できると思う。

"priority"はどの境界条件を優先するか？という意味でつけた。というのも、例えば、vertexes[1]の頂点上の境界条件がbc["bctype"][0]、bc["bctype"][1]どっちを使うか？　というのを指定するためのものだ。
"priority"は優先度を順にリストで格納するとルール付けた。このへんも、人によってどういうルールで実装するのが良いかは異なると思うので、あまり詳しい説明はしない。

さらに、多角形を含む直角形を計算するcalcRangeと、デバッグ用にplotする、plotを追加した。わざわざ書くまでもないので省略する。

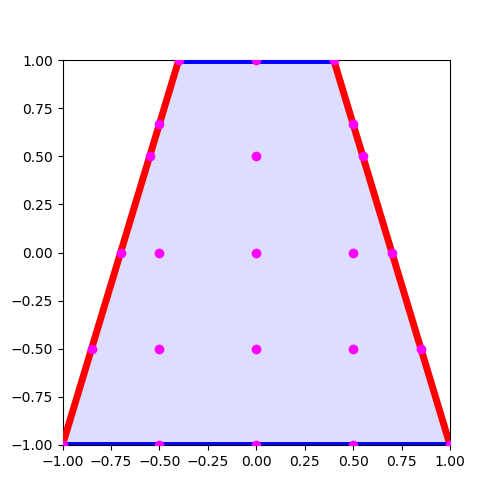
これによって、次の図が得られた。

図3:Domainクラスのplot

よし、これで計算領域は設定完了だ。

ソース項の指定(Problemクラス)

次は、Sourceクラスを作っていこう。
これは単純明快で(二次元配列を引数とする)式を引数にすればいい。
Sourceクラス自体のソースは次のようになる。

Source.py

import numpy as np

class Source(object):
    def __init__(self, source):
        self.source=source

……あれ、一行で収まってしまった。
こんなクラス分けは良くないと思う…。みんなはこうならないように気をつけよう！
ちょっと話はズレるが、pythonはクラスのメンバ変数を外部から直接変更、取得できるので、getter, setterがなくても良いと思っている。
pythonは手軽に使うためのものという印象が自分の中であるため、こういうところは素晴らしいと思う。プロトタイプをpython, 本番をC++などを使うとか、個人的にはアリ。

ところで、このままだと、例えばソース項を$0$にする場合でも無名関数lambdaを用いて、function = lambda x: 0を引数として与えなければならない。
それはちょっと面倒なので、ソース項が定数項の場合は定数を渡しても大丈夫なように編集しよう。
コードは以下のように変更される。

Source.py

import numpy as np

class Source(object):
    def __init__(self, source):
        print("-----Source-----")
        if isinstance(source, (int, float)):
            self.source = lambda x: source
        else:
            self.source = source

これで、引数sourceがint型、float型のときは定数関数として動作しそうだ。

Domain, Sourceの呼び出し(Problemクラス)

まとめも兼ねて、Domain, SourceクラスをまとめるProblemクラスについて簡単に書いていこう。

Problem.py

from . import Domain
from . import Source

class Problem(object):
    def __init__(self, problem):
        self.setDomain(**problem["domain"])
        self.setSource(problem["source"])

    def setDomain(self, **domain):
        if domain["shape"]=="Polygon":
            self.domain=Domain.Polygon(domain["vertexes"], domain["bc"])
            self.domain.calcRange()
    def setSource(self, source):
        self.source=Source.Source(source)

引数についても簡単に説明しておこう。次のページに引数の例を書いている。

setDomain(
    shape = "Polygon" 
    vertexes = np.array([[-1,-1], [1,-1], [0.4,1],[-0.4,1]])
    bc = {"bc": [{"bctype":"Dirichlet", "constant": 1},
                 {"bctype":"Neumann"  , "constant": 0},
                 {"bctype":"Dirichlet", "constant":-1},
                 {"bctype":"Neumann"  , "constant": 0}]
          "priority":[0,2,1,3]}}
)
# sourceを定数関数f=0とする場合
setSource(
    source = 0
)
# sourceをsin(x)*sin(y)のようにする場合
setSource(
    source = lambda x: np.sin(x[0])*np.sin(x[1])
)

これらの関数を、PoissonEquationクラスから呼び出せばOKだ。

Step 2：格子生成

次は領域を格子分割する。正直、これが一番難しかった……。
この項はあまり細かいアルゴリズムなどには触れず、どういう意図でどういう仕様にしたか、ということに主眼を据えて話していこうと思う。
というのも、計算幾何学の方に寄りすぎてしまうため、ちょっと本題からずれるかな？と思ったためである。
もちろん、格子分割の仕方もFDMの奥深いところの一つではあるのだが、あまりに深すぎるので、ちょっと今回は置いておいて、最低限の話にする。気になる人は色々な本や論文から勉強してね。

以下の4つのステップで作った。

1. $x$軸、$y$軸に水平な格子点(ノード)の配置
2. 境界にノードを置く
3. 領域外のノードを消す
4. 隣のノードの定義

格子点の操作(Nodeクラス)

ステップ1. ノードを置こう

当初、NodeクラスとNodeManagementクラスに分けようと考えていたが、よく考えるとpythonには辞書型というものがある。
各格子点(ノード)のパラメータは辞書型で保管して、Nodeクラスはそれらの集合を操作するクラスにしよう。

ノードのパラメータは次のようにした。

node={
    "point":np.array(point), 
    "position":"nd", 
    "nextnode":[
        {"no":None, "position":"nd"}, 
        {"no":None, "position":"nd"}, 
        ... 
        ] 
    }

それぞれの説明を以下にまとめる

• "point": ノードの座標
• "position": ノードの位置関係("nd":定義なし　"in":領域内　"b(数字n)": 境界n上にある　"v(数字n)": 頂点n上にある)
• "nextnode": 隣のノードの情報のリスト
  • "no": 隣のノードのインデックス
  • "position": 隣のノードの位置関係("n":定義なし　"l":左　"r": 右　"d": 下　"u": 上)

Cartesianの__init__(コンストラクタ)の引数には、Domainインスタンスと、分割数(変数名divと名付ける)が必要になる。
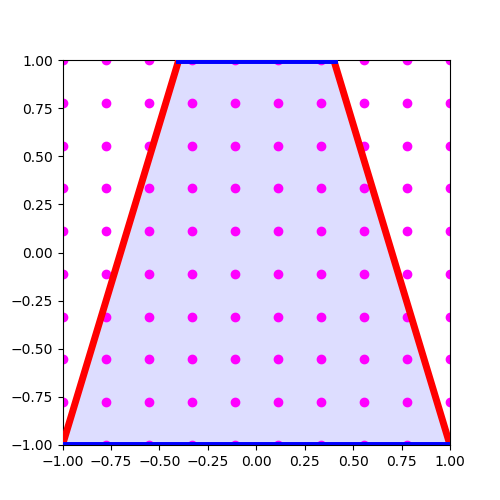
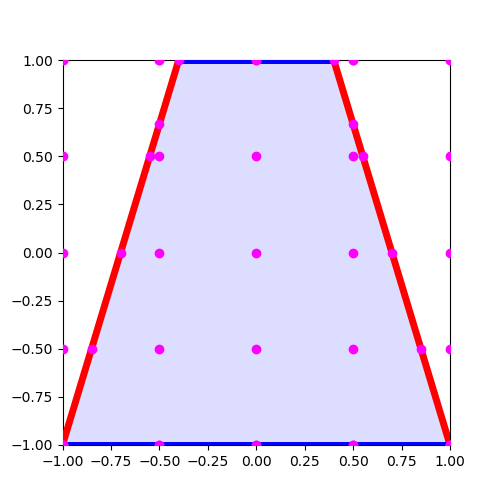
例えば、[10,10]を渡すと、縦横10等分されるように設定しよう。すると、こうなる。

図4：等間隔グリッド

また、ときには等分じゃないのも試してみたいということもあるだろう(え？ない？)。
例えば、[[-10,-7,-3,-1,0,1,3,7,10],[-10,-7,-3,-1,0,1,3,7,10]]のように渡すとうまいこと処理してくれて、

図5：非等間隔グリッド

のような、グリッドを分けてくれるようにしてみた。
実務では使わないかもしれないが、研究のためなら良いだろう。
さて、これは次のようにして実現できる。

class Cartesian(Node):
    def __init__(self, domain, div):
        np.array(div)
        if isinstance(div[0], (int)):
            self.nDivX = div[0]
            self.xs = np.linspace(domain.left, domain.right, self.nDivX)
        else:
            self.nDivX = len(div[0])
            self.xs = np.array(div[0])
            self.xs = np.sort(self.xs)
            d = (domain.right - domain.left) / (self.xs[-1] - self.xs[0])
            self.xs = d * self.xs
        if isinstance(div[1], (int)):
            self.nDivY = div[1]
            self.ys = np.linspace(domain.down, domain.up   , self.nDivY)
        else:
            self.nDivY = len(div[1])
            self.ys = div[1]
            self.ys = np.sort(self.ys)
            d = (domain.up - domain.down) / (self.ys[-1] - self.ys[0])
            self.ys = d * self.ys
        self.nDiv = self.xs * self.ys
        self.nodes = [{"point":np.array([self.xs[i],self.ys[j]]), "position":"nd", "nextnode":{"no":None, "position":"nd"} } 
                    for j,i in itertools.product(range(self.nDivX), range(self.nDivY))]

面倒なので、わざわざ説明しない。読者の皆様ならもう自分のやり方で、自分で作れるだろう。
とりあえず、上図のようなノードを作ってくれるものを作ったと思ってくれればいい。

ステップ2. 境界上にノードを置こう

つぎは、境界上にノードを置いていく。
すでにあるノードと重なっても関係ない。とにかく、現存するノードの$x$,$y$軸の水平線と交差する場所に置いていく。
これは、DomainクラスのほうにgetBorderPointとして作った。というのも、今回はPolygonだが、形状によってアルゴリズムが変わったと思ったからだ。

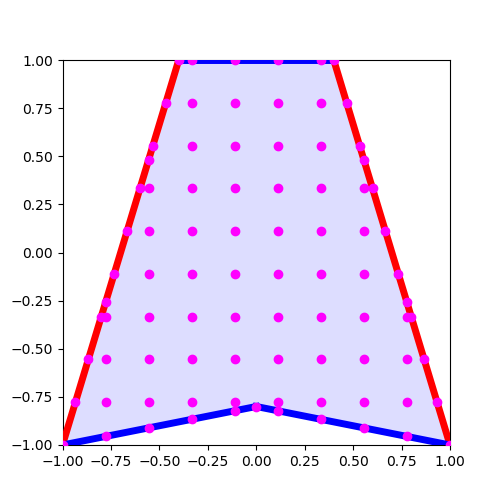
境界上にノードを置いたあと、重なったノードを消すと、次の図のようになる。

図5：境界を配置したもの

…色の設定をミスったなぁ。赤の境界とマゼンタのノードが重なってて見にくいかもしれないが……、我慢してほしい。
左から二番目、上から二番目のノードが境界ととても近いのがわかる。
これは、最後にテストしたときに気づいたのだが、大きな誤差の原因となるため、消すのが妥当である。
どれくらい近いものを消すか？　というものは引数として与えられるようにしとこう。

サラッと書いたが、意外と面倒だった……。ソースを見たい人はgithubで見てほしい。

ステップ3. 外側のノードを消そう

次に、内部判定処理をして、計算領域外部のノードを消していく。
まずはそれぞれの内外の判定をしないといけないのだが…、これは色んなアルゴリズムが既に提案されている。
ちなみに、今回は境界上のノードは上のプロセスで"position":"b"+(数字n)とデータ上に保存されているので、"position":ndのところのみを編集すれば良い。
境界上のノードでの内外判定は処理が結構面倒だったりするので、これはとても助かる。

有名な手法は２つある。
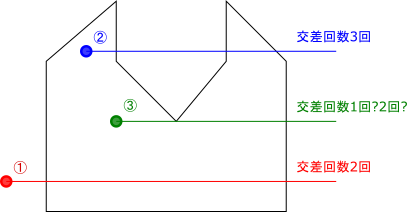
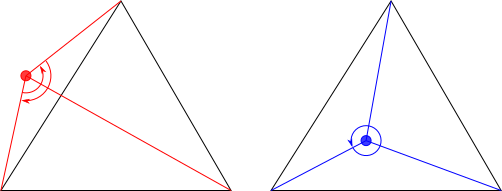
一つは判定する点から任意の方向に半直線を引き、境界と交差する回数を数える方法だ(Crossing Number Algorithm)。
交差する回数が偶数なら外部、奇数なら内部となる。

図6：Crossing Number Algorithm

この手法は四則演算のみなので早いが、気をつけなければいけないこともある。
上図の③の例を見ればわかるだろうが、線分に頂点が接する場合どうするか？ということを考えなければならない。
実際には「ぶつかった境界の線分のベクトルはどっち向きか？」という条件を課せば良いのだが、なんとなく面倒そうだ。

なので、今回はもう一つのWinding Number Algorithmという手法を採用しよう。
これは、判定する点からみて、各頂点間の角度の和が$2π$なら内部、$0$なら外部というものだ。

図7：Winding Number Algorithm

この手法は逆三角関数を利用するため、少々時間がかかるが、上記のような条件を考える必要がない。

さて、プログラムを書くのだが、それぞれのノードでforループを回すのは芸がない。
せっかくnumpyを使ってるのだから、なんとか行数を少なくして計算コストを減らしていこう。

プログラムは下記のようにした。

class Polygon(Domain):
    # 省略
    def deleteOutDomain(self, node, thetaerr=0.1):
        pts = np.array([node[i]["point"] for i in range(len(node))])    #["point"]をnumpyに置き直し
        pos = np.array([node[i]["position"] for i in range(len(node))]) #["position"]をnumpyに置き直し
        thetas = 0
        for i in range(len(self.vertexes)):
            p1 = self.vertexes[i]                           # 線分の端点1 p1
            p2 = self.vertexes[(i + 1) % self.nVertexes]    # 線分の端点2 p2
            v1 = (pts - p1)                                 # 判定したい点からp1へのベクトル
            v2 = (pts - p2)                                 # 判定したい点からp2へのベクトル
            dot = v1[:,0] * v2[:,0] + v1[:,1] * v2[:,1]     # 内積(dot, innerだと狙ったようにならなかった…)
            cross = v1[:,0] * v2[:,1] - v1[:,1] * v2[:,0]   # 外積(上と同じ)
            vn1 = np.linalg.norm(v1, axis=1)                # v1の距離取得
            vn2 = np.linalg.norm(v2, axis=1)                # v2の距離取得
            theta = np.arccos(np.clip(dot / (vn1 * vn2), -1, 1)) # 数値誤差により1より多くなることがあるため、clip
            thetas += np.sign(cross)*np.array(theta)        # 角度をforのたびに足していく(crossはプラス・マイナス判定)
        inx = np.where( ((pos == "nd") & ~(thetas < thetaerr)))[0]  # ["position"]がndでかつ、thetasがほぼ0じゃないもののインデックスを取得
        #省略

上手くやればvertexesのループすらも消すことができるのかもしれないが……、これくらいやれば許してくれると思う……。

結果は次のような結果になった。

図8：外側を消したもの

4. 隣のノードが何かを定義しよう

最後に、node[nextnode]を定義しよう。これを定義することによって次のステップの行列生成が簡単になる。

色々悩んだが、上下左右を座標で判断することにした。
浮動小数点の==(実際にはnp.isclose)が出てくるので、ホントはあまり良くないかもしれないが、これ以外に思い浮かばなかった。
本当は最初に整数でのindexをデータとして持っておくべきだったのかもしれないが……、まあ許してほしい。

と、その前に、nodeリストを座標でソートしておこう。そのほうが簡単だと思う。

わざわざ上げるまでもないのでgithubの方を参照してほしい。
(実はプログラムを作ると上で「forを使うな！」と言っておいて二重になってしまって恥ずかしいというのもある…)

ここまで出来て、nodeリストの結果を出力してみよう。
データ数が多すぎても網羅的に見れないので、div=[4,4]あたりで出してみよう。

node0 {'point': array([-1., -1.]), 'position': 'c0', 'nextnode': [{'no': 1, 'position': 'r'}]}
node1 {'point': array([-0.333, -1.   ]), 'position': 'b0', 'nextnode': [{'no': 5, 'position': 'u'}, {'no': 0, 'position': 'l'}, {'no': 2, 'position': 'r'}]}
node2 {'point': array([ 0.333, -1.   ]), 'position': 'b0', 'nextnode': [{'no': 6, 'position': 'u'}, {'no': 1, 'position': 'l'}, {'no': 3, 'position': 'r'}]}
node3 {'point': array([ 1., -1.]), 'position': 'c1', 'nextnode': [{'no': 2, 'position': 'l'}]}
node4 {'point': array([-0.8  , -0.333]), 'position': 'b3', 'nextnode': [{'no': 5, 'position': 'r'}]}
node5 {'point': array([-0.333, -0.333]), 'position': 'in', 'nextnode': [{'no': 1, 'position': 'd'}, {'no': 9, 'position': 'u'}, {'no': 4, 'position': 'l'}, {'no': 6, 'position': 'r'}]}
node6 {'point': array([ 0.333, -0.333]), 'position': 'in', 'nextnode': [{'no': 2, 'position': 'd'}, {'no': 10, 'position': 'u'}, {'no': 5, 'position': 'l'}, {'no': 7, 'position': 'r'}]}
node7 {'point': array([ 0.8  , -0.333]), 'position': 'b1', 'nextnode': [{'no': 6, 'position': 'l'}]}
node8 {'point': array([-0.6  ,  0.333]), 'position': 'b3', 'nextnode': [{'no': 9, 'position': 'r'}]}
node9 {'point': array([-0.333,  0.333]), 'position': 'in', 'nextnode': [{'no': 5, 'position': 'd'}, {'no': 13, 'position': 'u'}, {'no': 8, 'position': 'l'}, {'no': 10, 'position': 'r'}]}
node10 {'point': array([0.333, 0.333]), 'position': 'in', 'nextnode': [{'no': 6, 'position': 'd'}, {'no': 14, 'position': 'u'}, {'no': 9, 'position': 'l'}, {'no': 11, 'position': 'r'}]}
node11 {'point': array([0.6  , 0.333]), 'position': 'b1', 'nextnode': [{'no': 10, 'position': 'l'}]}
node12 {'point': array([-0.4,  1. ]), 'position': 'c3', 'nextnode': [{'no': 13, 'position': 'r'}]}
node13 {'point': array([-0.333,  1.   ]), 'position': 'b2', 'nextnode': [{'no': 9, 'position': 'd'}, {'no': 12, 'position': 'l'}, {'no': 14, 'position': 'r'}]}
node14 {'point': array([0.333, 1.   ]), 'position': 'b2', 'nextnode': [{'no': 10, 'position': 'd'}, {'no': 13, 'position': 'l'}, {'no': 15, 'position': 'r'}]}

うん、いい感じ……あ！　忘れてた。
境界上のノードの隣はf(forward)とb(back)として表したいと思っていたんだ。境界上は斜めだったりするので、上下左右だけでは表せないのである。
ということでもう一度プログラムを確認した。

node0 {'point': array([-1., -1.]), 'position': 'c0', 'nextnode': [{'no': 1, 'position': 'f'}, {'no': 4, 'position': 'b'}, {'no': 1, 'position': 'r'}]}
node1 {'point': array([-0.333, -1.   ]), 'position': 'b0', 'nextnode': [{'no': 0, 'position': 'b'}, {'no': 2, 'position': 'f'}, {'no': 0, 'position': 'l'}, {'no': 2, 'position': 'r'}]}
node2 {'point': array([ 0.333, -1.   ]), 'position': 'b0', 'nextnode': [{'no': 1, 'position': 'b'}, {'no': 3, 'position': 'f'}, {'no': 1, 'position': 'l'}, {'no': 3, 'position': 'r'}]}
node3 {'point': array([ 1., -1.]), 'position': 'c1', 'nextnode': [{'no': 2, 'position': 'b'}, {'no': 7, 'position': 'f'}, {'no': 2, 'position': 'l'}]}
node4 {'point': array([-0.8  , -0.333]), 'position': 'b3', 'nextnode': [{'no': 0, 'position': 'f'}, {'no': 8, 'position': 'b'}, {'no': 5, 'position': 'r'}]}
node5 {'point': array([-0.333, -0.333]), 'position': 'in', 'nextnode': [{'no': 4, 'position': 'l'}, {'no': 6, 'position': 'r'}]}
node6 {'point': array([ 0.333, -0.333]), 'position': 'in', 'nextnode': [{'no': 5, 'position': 'l'}, {'no': 7, 'position': 'r'}]}
node7 {'point': array([ 0.8  , -0.333]), 'position': 'b1', 'nextnode': [{'no': 3, 'position': 'b'}, {'no': 11, 'position': 'f'}, {'no': 6, 'position': 'l'}]}
node8 {'point': array([-0.6  ,  0.333]), 'position': 'b3', 'nextnode': [{'no': 4, 'position': 'f'}, {'no': 12, 'position': 'b'}, {'no': 9, 'position': 'r'}]}
node9 {'point': array([-0.333,  0.333]), 'position': 'in', 'nextnode': [{'no': 8, 'position': 'l'}, {'no': 10, 'position': 'r'}]}
node10 {'point': array([0.333, 0.333]), 'position': 'in', 'nextnode': [{'no': 9, 'position': 'l'}, {'no': 11, 'position': 'r'}]}
node11 {'point': array([0.6  , 0.333]), 'position': 'b1', 'nextnode': [{'no': 7, 'position': 'b'}, {'no': 15, 'position': 'f'}, {'no': 10, 'position': 'l'}]}
node12 {'point': array([-0.4,  1. ]), 'position': 'c3', 'nextnode': [{'no': 13, 'position': 'b'}, {'no': 8, 'position': 'f'}, {'no': 13, 'position': 'r'}]}
node13 {'point': array([-0.333,  1.   ]), 'position': 'b2', 'nextnode': [{'no': 12, 'position': 'f'}, {'no': 14, 'position': 'b'}, {'no': 12, 'position': 'l'}, {'no': 14, 'position': 'r'}]}
node14 {'point': array([0.333, 1.   ]), 'position': 'b2', 'nextnode': [{'no': 13, 'position': 'f'}, {'no': 15, 'position': 'b'}, {'no': 13, 'position': 'l'}, {'no': 15, 'position': 'r'}]}
node15 {'point': array([0.4, 1. ]), 'position': 'c2', 'nextnode': [{'no': 11, 'position': 'b'}, {'no': 14, 'position': 'f'}, {'no': 14, 'position': 'l'}]}

よし、OKだ。
ちょっと形状を変えて試してみよう。

図9：形状を変えた場合

いい感じ。

Step 3：FDMソルバー

行列を作る(MatrixGenerater)

とうとうここまで来た。
あとは行列を作るだけ…なのだが、ここで２つ問題がある。

計算領域内部の離散式

１つ目は、前回導出した離散式、
$$
\frac{u_{m-1,n} -2u_{m,n} + u_{m+1,n}}{\Delta_x^2} + \frac{u_{m,n-1} -2u_{m,n} + u_{m,n+1}}{\Delta_y^2} = f_{m,n} + \mathcal{O}(\Delta_{x,y}^2)
$$
左右(上下)で同じ間隔という過程で導出したものだ。
しかし、今回の格子は境界の隣で非等間隔となってしまっている。
といってもこれは簡単に解決できて、同じくテイラー展開をうまいこと変形すればいいだけだ。
計算してみよう。

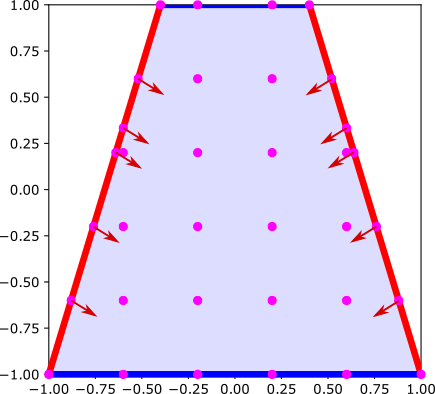
以下の図のように左、右、上、下のノード間隔を$\Delta_l, \Delta_r, \Delta_u. \Delta_d$と置く。
このとき、それぞれの点の$u$の値を$u_l, u_r, u_u. u_d$とし、その中心$u_0$としてそれぞれテイラー展開をすると、次のようになる。

\begin{align}
u_l &= u_0 - \Delta_l \frac{\partial u_0}{\partial x} + \frac{\Delta_l^2}{2} \frac{\partial^2 u_0}{\partial x^2} -\frac{\Delta_l^3}{6} \frac{\partial^3 u_0}{\partial x^3} + \mathcal{O}(\Delta_x^4) \\
u_r &= u_0 + \Delta_r \frac{\partial u_0}{\partial x} + \frac{\Delta_r^2}{2} \frac{\partial^2 u_0}{\partial x^2} +\frac{\Delta_r^3}{6} \frac{\partial^3 u_0}{\partial x^3} + \mathcal{O}(\Delta_x^4) \\
u_d &= u_0 - \Delta_u \frac{\partial u_0}{\partial y} + \frac{\Delta_u^2}{2} \frac{\partial^2 u_0}{\partial y^2} -\frac{\Delta_u^3}{6} \frac{\partial^3 u_0}{\partial y^3} + \mathcal{O}(\Delta_y^4) \\
u_u &= u_0 + \Delta_d \frac{\partial u_0}{\partial y} + \frac{\Delta_d^2}{2} \frac{\partial^2 u_0}{\partial y^2} +\frac{\Delta_d^3}{6} \frac{\partial^3 u_0}{\partial y^3} + \mathcal{O}(\Delta_y^4)
\end{align}

あとはうまいこと足し引きして、一階微分の項を消していくと、次のように求まる。

\begin{align}
\frac{\partial^2 u}{\partial x^2} &= \frac{2}{\Delta_l \Delta_r(\Delta_l + \Delta_r)}\left( \Delta_r(u_l - u_0) + \Delta_l (u_r - u_0) \right) + \mathcal{O}(\Delta_x)\\
\frac{\partial^2 u}{\partial y^2} &= \frac{2}{\Delta_d \Delta_u(\Delta_d + \Delta_u)}\left( \Delta_u(u_d - u_0) + \Delta_d (u_u - u_0) \right) + \mathcal{O}(\Delta_y)
\end{align}

残念ながら精度は一次精度となってしまったが、仕方ない。
あとはポアソン方程式に代入すれば、次式が求まる。

\begin{multline}
\frac{2}{\Delta_l \Delta_r(\Delta_l + \Delta_r)}\left( \Delta_r(u_l - u_0) + \Delta_l (u_r - u_0) \right) \\+ \frac{2}{\Delta_d \Delta_u(\Delta_d + \Delta_u)}\left( \Delta_u(u_d - u_0) + \Delta_d (u_u - u_0) \right) = f + \mathcal{O}(\Delta_{x,y})
\end{multline}

見た目は面倒だが、コンピュータならすぐに計算してくれる。

一つ注意してみてほしいのは、$\mathcal{O}(\Delta)$の項の大きさだ。
直感的にわかると思うが、左右(上下)の間隔の違いが大きいほど、誤差が大きくなる。
実際に計算して見ると、たしかに$\Delta_l$と$\Delta_r$の差が大きいと、その分$\mathcal{O}(\Delta_x)$が大きくなることがわかる。そんなに難しくないし、暇な人は計算してみてほしい(暗算でも分かる人はわかると思う)。

逆に言うと、格子間隔はなるべく同じの方が良いわけだ。
図5のようなものは実は良くない。本当はノードを増やすか、逆に減らすかしたほうが良い。

境界上の離散式

もう一つの問題のほうが厄介だ。
前回導出したノイマン境界条件の近似式

\begin{align}
\frac{u_{m+1,n} - u_{m,n}}{\Delta_x} = g \\
\frac{u_{m,n+1} - u_{m,n}}{\Delta_y} = g
\end{align}

は、あくまで境界が$x, y$軸と垂直の場合(つまり、$x$もしくは$y$の偏微分)の近似式であり、今回のようなちょっと斜めな場合には使えない。

図10：斜めの境界条件

上図の矢印の方向に運良くノードがあればいいが、そんなこともない。
そこで、もう一度基本に立ち返ってテイラー展開から考えてみよう。

と、その前に
$$
\frac{\partial u}{\partial n}
$$
は、$u$の境界の垂直方向の微分で、
$$
\frac{\partial u}{\partial n} = \nabla u \cdot \boldsymbol{n}
$$
と表すこともできるということを確認しておこう。この$\boldsymbol{n}$は境界と垂直方向の長さが1のベクトル(単位法線ベクトル)である。
例えば。上記の図の左側の境界については次のように書き下せる。
$$
\frac{\partial u}{\partial n} = \frac{2}{\sqrt{0.6^2 + 2^2 } }\frac{\partial u}{\partial x} - \frac{0.6}{\sqrt{0.6^2 + 2^2 } }\frac{\partial u}{\partial y}
$$
(上の図では正確にはわからないが、上辺は-0.4から0.4の線分である。そういえば、大学のゼミではわかりにくいからそういう図にするなとよく言われた……。正しい言い分だが、まあ今回は個人の趣味レベルの記事だし……言い訳)

つまり、なんとかして以下の離散化を行えば良いことになる。
$$
\frac{\partial u}{\partial n} = a\frac{\partial u}{\partial x} + b\frac{\partial u}{\partial y} \tag{1}
$$
ここで出てくるのが、二次元のテイラー展開だ。
ちょっと覚えていないかもしれないので、文字をわかりやすいように置き直してここに書いておこう。

\begin{align}
u_{r, s}&=\sum_{p=0}^\infty \frac{1}{p!}\left( r \frac{\partial}{\partial x}  + s \frac{\partial}{\partial y} \right)^p u_0 \\
&=u_{0,0} + r \frac{\partial u_0}{\partial x}  + s \frac{\partial u_0}{\partial y}  + \cdots
\end{align}

この第二項と第三項を上手いこと式(1)と同じにすればいい。
これは、２点でテイラー展開をした２つの式を連立させればいい。敢えて冗長に書くと、

\begin{align}
u_{r_1, s_1}=u_{0,0} + r_1 \frac{\partial u_0}{\partial x}  + s_1 \frac{\partial u_0}{\partial y}  + \cdots \\
u_{r_2, s_2}=u_{0,0} + r_2 \frac{\partial u_0}{\partial x}  + s_2 \frac{\partial u_0}{\partial y}  + \cdots
\end{align}

を足したり引いたりして、３項目と４項目を式(1)にすれば良いのである。
つまり、次の式を$c_1$, $c_2$について解けばいい。

\begin{align}
r_1c_1 + r_2c_2 = a \\
s_1c_1 + s_2c_2 = b
\end{align}

$c_1$, $c_2$について解けば、以下のように近似できる。

$$
a \frac{\partial u_0}{\partial x} + b \frac{\partial u_0}{\partial y} = c_1 u_{r_1, s_1} + c_2 u_{r_2, s_2} - (c_1 + c_2) u_{0,0} + \mathcal{E}
$$

$\mathcal{E}$は誤差を表している。適切な書き方がわからなかったので、適当に書いた。

さて、ここまでできたらもう簡単だ。
$u_{r_1, s_1}$, $u_{r_2, s_2}$は、境界に近い２つを利用しよう。これについての行列を作って、numpy.linalg.solveで解けばOKだ。

ただ、境界付近には3つノードあるし、２つで解くのはちょっともったいない。
２つで解けるなら当然３つならより精度良く解ける。

$$
\frac{\partial u}{\partial n} = g
$$

つまり、

$$
\left( k_1 \frac{\partial}{\partial x} + k_2 \frac{\partial}{\partial y} \right) \left(a\frac{\partial u}{\partial x} + b\frac{\partial u}{\partial y} \right) = \left( k_1 \frac{\partial}{\partial x} + k_2 \frac{\partial}{\partial y} \right) g
$$

が成り立つ。$g$が定数なら右辺は$0$だ。
$g=0$として、

$$
a\frac{\partial u}{\partial x} + b\frac{\partial u}{\partial y} +
k_1 a \frac{\partial^2 u}{\partial x^2} + (k_1 b + k_2 a)\frac{\partial^2 u}{\partial x \partial y} + k_2 b \frac{\partial u}{\partial y} = 0 \tag{2}
$$

である。この式を三点で作れば２次精度に達成できる。
一応、その三式を下に書き下しておこう。

\begin{align}
  u_{r_1, s_1}=u_{0,0} + r_1 \frac{\partial u_0}{\partial x}  + s_1 \frac{\partial u_0}{\partial y} + \frac{r_1^2}{2} \frac{\partial^2 u_0}{\partial x^2} + r_1s_1 \frac{\partial^2 u_0}{\partial x \partial y} + \frac{s_1^2}{2} \frac{\partial^2 u_0}{\partial y^2} + \cdots \\
  u_{r_2, s_2}=u_{0,0} + r_2 \frac{\partial u_0}{\partial x}  + s_2 \frac{\partial u_0}{\partial y} + \frac{r_2^2}{2} \frac{\partial^2 u_0}{\partial x^2} + r_2s_2 \frac{\partial^2 u_0}{\partial x \partial y} + \frac{s_2^2}{2} \frac{\partial^2 u_0}{\partial y^2} + \cdots \\
  u_{r_3, s_3}=u_{0,0} + r_3 \frac{\partial u_0}{\partial x}  + s_3 \frac{\partial u_0}{\partial y} + \frac{r_3^2}{2} \frac{\partial^2 u_0}{\partial x^2} + r_3s_3 \frac{\partial^2 u_0}{\partial x \partial y} + \frac{s_3^2}{2} \frac{\partial^3 u_0}{\partial y^2} + \cdots
\end{align}

式(2)は5項なのに対し、3式で解けるのか、というふうに思うかも知れないが、$k_1$, $k_2$は任意の値なのでなんとかなる。
連立方程式として書き下してみよう。
まず、各項に係数をかけて足した、次の項ができる。

\begin{equation}
    \left\{
\begin{alignedat}{5}
 r_1  &c_1& + r_2   &c_2 &+ r_3   c_3&=& a  \\
 s_1  &c_1& + s_2   &c_2 &+ s_3   c_3&=& b  \\
 r_1^2&c_1& + r_2^2 &c_2 &+ r_3^2 c_3&=& 2 k_1a  \\
 r_1 s_1  &c_1& + r_2 s_2 &c_2 &+ r_3 s_3   c_3&=& k_1 b + k_2 a  \\
 s_1^2&c_1& + s_2^2 &c_2 &+ s_3^2 c_3&=& 2 k_2b 
\end{alignedat}
    \right.
\end{equation}

この、$k_1$, $k_2$も変数として見れば、5変数、5式の方程式となる。行列に書き直すと、次のような式にすることができる

\begin{equation}
\left[ 
    \begin{matrix}
        r_1     & r_2   & r_3   & 0   & 0   \\
        s_1     & s_2   & s_3   & 0   & 0   \\
        r_1^2   & r_2^2 & r_3^2 & -2a & 0   \\
        r_1s_1  & r_2s_2& r_3s_3& -b  & -a  \\
        s_1^2   & s_2^2 & s_3^2 & 0   & -2b   \\
    \end{matrix}
\right]\left[ 
    \begin{matrix}
        c_1 \\
        c_2 \\
        c_3 \\
        k_1 \\
        k_2
    \end{matrix}
\right] =
\left[ 
    \begin{matrix}
        a \\
        b \\
        0 \\
        0 \\
        0
    \end{matrix}
\right]
\end{equation}

これならなんとか解けそうだ。

Step 4：結果の出力

さて、最後に結果を出力する。

人に成果を見せるという意味でも一番重要だし、開発者がわからしてもとても楽しみなところだ。
しかし、ここで悪い結果が出ると絶望感がすごい。いや、一回目で成功するなんてことはまずないのだが……。

電位(Potential)

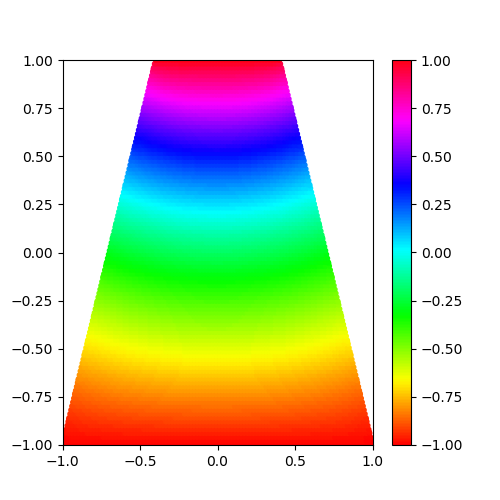
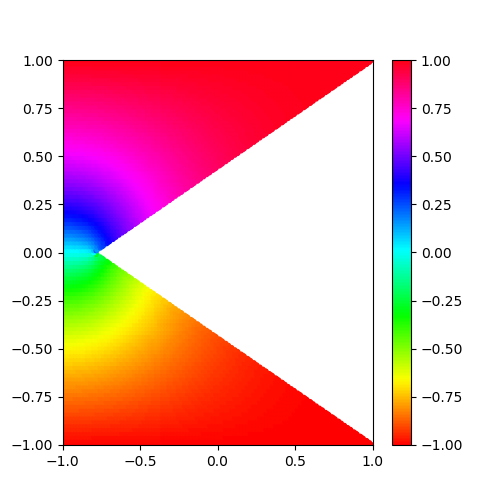
結果を想定する前に、ちょっと答えを想像してみよう。
問題は台形の上辺と下辺がディリクレ境界条件でそれぞれ1、-1だった。
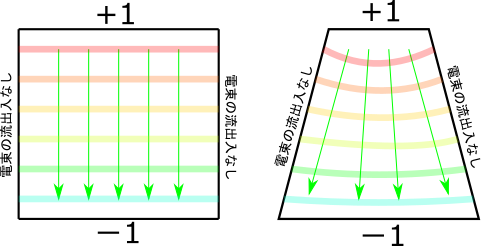
もし正方形だったらどうなるだろう？　これは実は理想状態のコンデンサと全く同じ、すなわち上から下まで電界は一定で、電位は比例関係となる。
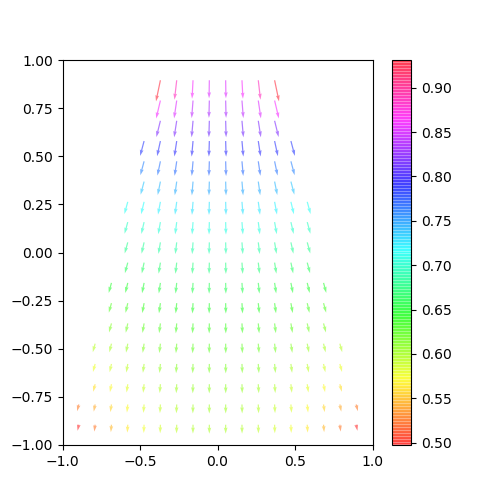
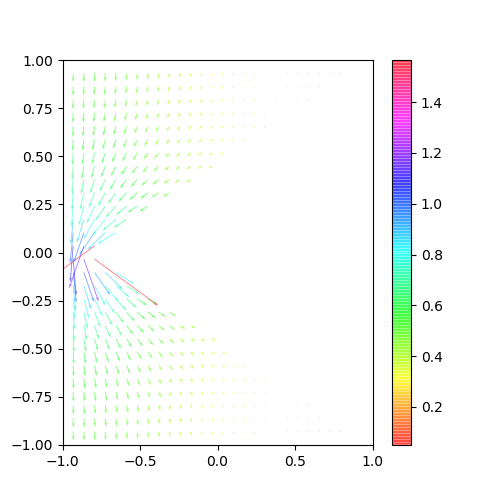
なら、上辺が小さくなったら……ということで、下にイメージ図を書いてみた。

図10：解のイメージ図

緑の矢印が電界で、虹色の薄い線はそれぞれ電位の等高線を表している。
こんな感じになれば正解という当たりをつけることが出来た！
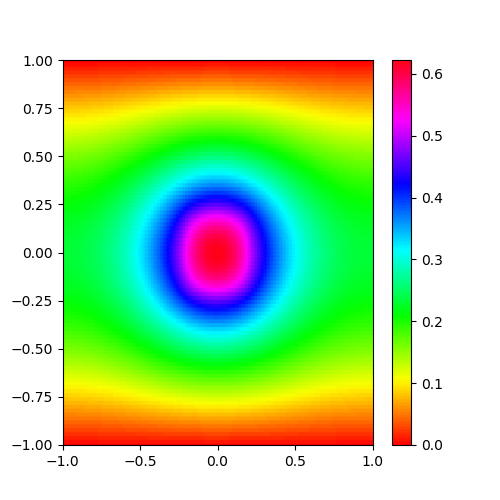
とりあえず、100×100でやってみた。

一回に出来たように書いてるが、何度もバグ潰ししたり、工夫をして修正した賜物だ。

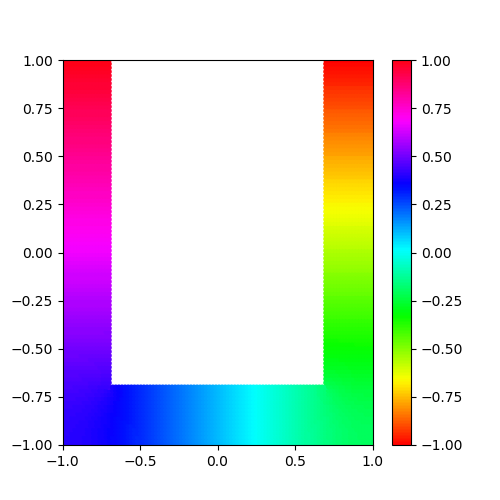
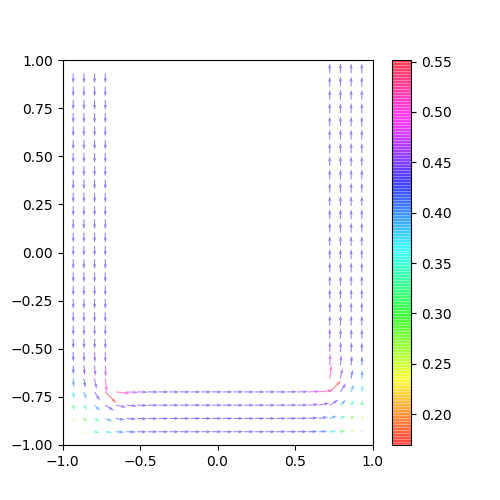
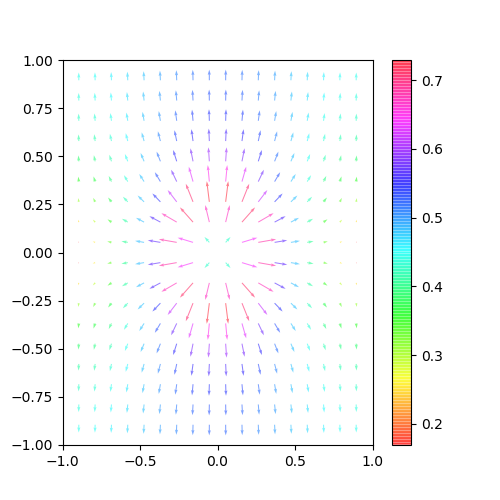
電場(FluxDensity)

電場も出力してみよう。
今回は格子点上の電場を周りの4つの電位から計算することにする。
つまり、

\begin{align}
\left. \frac{\partial u}{\partial x} \right|_{m,n} = \frac{1}{2\Delta_x}(u_{m+1, n} - u_{m-1, n}) \\
\left. \frac{\partial u}{\partial y} \right|_{m,n} = \frac{1}{2\Delta_y}(u_{m, n+1} - u_{m, n-1})
\end{align}

のように計算する。
結果は以下のようになった。

とてもいい感じだ。
理論解との比較などもやりたかったが、今回は長くなってしまったのでやめておく。またいつか気が向いたら……。

ポアソン方程式クラス

上記をすべて総括した、PoissonEquationクラスを作った。

# 省略
if __name__ == "__main__":
    #Step 1: Problem
    domain = {"shape":"Polygon",
              "vertexes":[[-1,-1],[1,-1], [0.4,1],[-0.4,1]],
              "bc":{
                  "bc": [
                      {"bctype":"Dirichlet", "constant":-1}, 
                      {"bctype":"Neumann", "constant":0},
                      {"bctype":"Dirichlet", "constant":1},
                      {"bctype":"Neumann", "constant":0}
                      ], 
                  "priority":[0,2,1,3]
                  }
              }
    source = {"source": 0}
    poisson = PoissonEquation(domain,source)

    # Step 2: generateGrid
    grid = {"type":"Cartesian", "div":[25,25]}
    poisson.generateGrid(grid, "Node")

    # Step 3: Solve
    method = "FDM"
    poisson.solve(method)

    # Step 4: Result
    poisson.result()
    poisson.plot("Potential")
    poisson.plot("DensityFlux")

まとめ

今回は次の4つに分けてポアソン方程式のFDMソルバーを設計・開発した。

• 問題クラス(Problem)
• 格子クラス(Grid)
• ソルバークラス(Solver)
• 結果クラス(Result)

今回作ったプログラムは、以下のURLに乗せてある。

[https://github.com/atily17/PoissonEquation]

numpyとmatplotlibさえあれば動くと思う。
テストなどはほとんどしていないので、しっかりと動作する保証はしない。
多分、問題条件を少し変えたら一気に崩れると思う。バグの修正希望があれば出してください。気が向いたら直します。

TODO

次の記事は有限要素法(FEM)の話にしようと思う。
といっても、FDMはまだ語り足りないところもあるので、ここにキーワードだけ書いておこう。いつか気が向いたときに記事にしようと思う。

• 直交座標系以外の座標系
  • 極座標系
  • 曲線座標系
• 無限遠点の境界条件の解析法
  • Boundary Relaxation Method
• 高次精度FDM
  • 四次精度の定式化
  • Compact Stencil 四次精度
• 非構造格子FDM
  • サブグリッド

ギャラリー

U字型の例

狭い

(ちょっと不安定な感じがある…)

真ん中に電荷