はじめに
サンプリング定理(標本化定理)は誤解されやすいと思ってます。
私も誤った理解をしてましたし、現在も理解したとは言い難い状況です。
それでも私が現在理解した範囲を解説することによってサンプリング定理の誤解が少しでも減らせたらと思ってこの記事を書いてみました。
素人がサンプリング定理を解説しようという無謀な企画です。
今回はオーディオ関連を念頭においています。
対象読者
サンプリング定理になにか納得がいかない人
書いてる人
オーディオマニアです。
エンジニアではありません。
デジタル音声処理を学んだこともありません。
すべてネット上の情報の受け売りです。
お願い
間違った記載や誤解を招く表現があれば指摘してください。
私の能力が足りないので記事が改善できるかわかりませんが。
一番良いのはこれより分かりやすく正しい記事を誰か書いてくれることです。
参考文献
東京電機大学の金田先生の資料
https://www.kanedayyy.jp/asp/ASP/DSPseminar14.pdf
環境
計算・グラフ作成はLinux(Ubuntu)上のGNU Octave, version 8.4.0で行いました。
サンプリング定理とは
標本化(サンプリング)定理
- 元信号に含まれる最大周波数 fmax
- サンプリング周波数(標本化周波数) fs
- fs > 2・fmax または fmax < fs/2
- この条件を満たせば元の情報は失わない。( = 原信号を再現できる )
そのまま再構成されるわけではなく理想ローパスフィルタで高域をカット( = sinc関数で補完)する必要があります。
アップサンプリングしてデジタルフィルタで行うことが一般的です(例外あり)。
サンプリング定理のよくある誤解
具体的にどのサイトの記事が間違ってるという話ではありません。
私もこんな誤解をしていたということで「よくある」というのは個人的感想です。
- サンプリング定理は間違ってる、高い周波数になると明らかにサンプル数が足りない!
- サンプリング定理は正しいが、無限の長さから補完しなければならないから無理、意味がない
- サンプリング定理によって周波数情報は失われないが波形は再現できない
- サンプリング(離散化)すると時間情報が失われ、サンプリング間隔以下の短い時間差が再現できない
- 理想的な処理は無限の長さから補完する必要があるので無理、なら「僕の考えた最強の曲線」で補完してやるぜ!
こんなところでしょうか
なぜ誤解が生じるのか?
サンプリング定理の数学的証明はネット上でも見つけられます。
そしてそれは正しいです。
しかしなんというか、「直感に反している」のです。
特に時間軸で見ていると各サンプル間を直線で結べばカクカクだし、曲線で結ぼうとしても、無限に結ぶ方法がありそうに思えます。
正しいsinc関数で補完しようとしても必要な時間が長過ぎて現実的ではありません。
ある1点の値を求めるのに前後無限大の長さの信号が必要というのも直感的ではありません。
デジタルフィルタも時間軸の波形で見ると直感的な理解が難しいです。単純に打ち切った場合、窓関数の違いなどは周波数軸で見ないと判りにくいのです。
そこで 時間軸で見るのはやめて周波数軸で考える と直感的に分かりやすくなります。
これ以降は主に周波数軸で考えて、その後に時間軸で確認することにします。
サンプリング定理を周波数軸で考える
サンプリングされた離散信号から元波形を再現するには理想ローパスフィルタを通す必要があります。
理想ローパスフィルタ = sinc関数で補完 です。
ここを時間軸で考えて「sinc関数でサンプリング間を補完する」と考えると誤解しやすくなります。
周波数軸で考えましょう。
理想ローパスフィルタを使う意味
- 直線位相
- 帯域内の情報を欠落なくそのまま通す
- 帯域外はすべてノイズなので完全に取り除く
しかし理想ローパスフィルタは実現できません。
とくにアナログでは特性の良いフィルタを作ることは困難です。
そこで大抵のDAコンバータは内部でアップサンプリングして特性の良いデジタルフィルタを使っています。
したがって何も考えずに普通に再生すれば理想ローパスフィルタではではないけど適切な処理が行われてある程度サンプリング定理を満たせることになります。
ここでは理解を助けるためにどんなフィルタにすればよいか考えていきます。
なお位相については色々な意見がありますが、サンプリング定理の理解が目的なので直線位相とします。
なにを妥協するか
特性の良いデジタルフィルタでも理想ローパスフィルタは実現できません。
理想が実現できなければ、なんらかの妥協が必要となります。
どこをどれくらい妥協するのかがポイントです。
阻止帯域の減衰量
これは分かりやすい。
阻止帯域が−∞である必要はありません。
量子化bit数によって必要な減衰量が決まります。
sox(音声処理のスイスアーミーナイフ)の場合
- -125dB 16-bit mastering use with dither
- -175dB 24-bit mastering
とりあえず-175dB以上を目指します
遷移帯域をどうするか?
理想ローパスフィルタではないので当然遷移帯域があります。
これをどこに持ってくるか?
fs/2まで完全に再生するとどうしてもエイリアシングノイズが除去しきれません。
普通はエイリアシングノイズの除去を優先して通過帯域のほうを妥協するようです。
通過帯域の高域をカットする代わりにエイリアシングノイズをほぼ完全に除去するようにカットオフを設定します。
CDの規格(fs44.1kHz、高域は20kHzまで)とすれば通過帯域はfs/2の 90.7% となります。
この9.3%の余裕を遷移帯域に当てます。
帯域内のリプル
これは無いほうが良いでしょう。
簡単にフラットにできるし、ここを妥協する意味はありません。
実際のフィルタの例
フィルタの設計については理想のローパスフィルタと現実のフィルタを参照
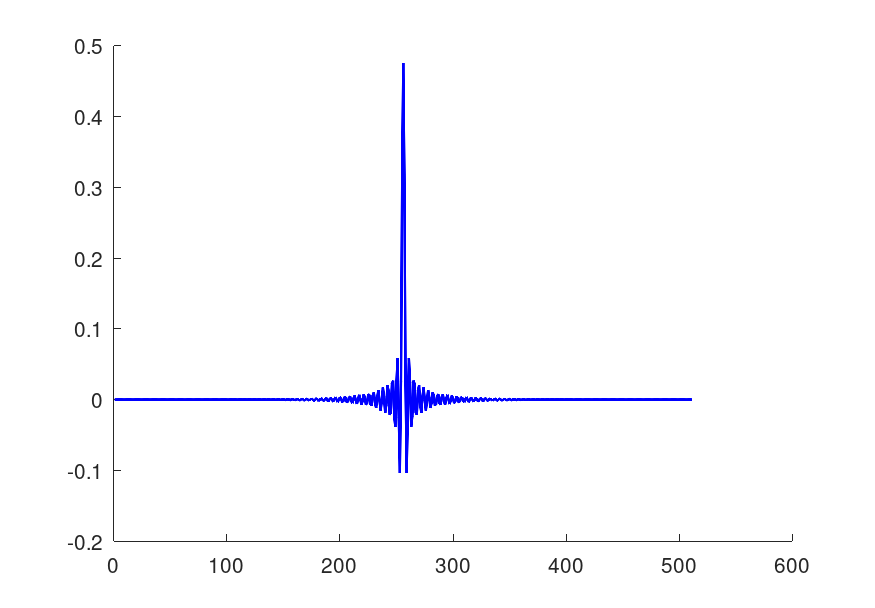
最後に作ったフィルタです。
フィルタの波形と特性
fs: 88200Hz
fc: 20940Hz
長さ511サンプル(時間にすれば0.0058秒)
窓関数: kaiser(β=20)
このようにエイリアシングノイズをほぼ完全に除去し、通過帯域も理論値の95%近く取ることができました。
この波形を畳み込むのを時間軸で考えてみます。
理想的な処理のsinc関数ではサンプリング点以外のサンプリング間隔の位置はゼロなので無限に補完していってもサンプリング点の値は変わりません。
しかしこの現実のフィルタで補完するとカットオフ周波数がfs/2より小さいのでサンプリング点の値も変わってしまいます。
それで良いの?と思うかもしれませんが、良いのです。
サンプリング点の値が変わってしまうのは高域がカットされている(通過帯域がfs/2の95%とか)ためです。
その代わりにエイリアシングノイズがほぼ完全に除去できているわけです。
波形が再現できるか確かめてみる
アナログ波形はコンピュータ上では扱えないのでアップサンプリングしたデータをアナログの代わりとします。
20kHz正弦波
20kHzの正弦波とそれを44100Hzでサンプリングしたものです。
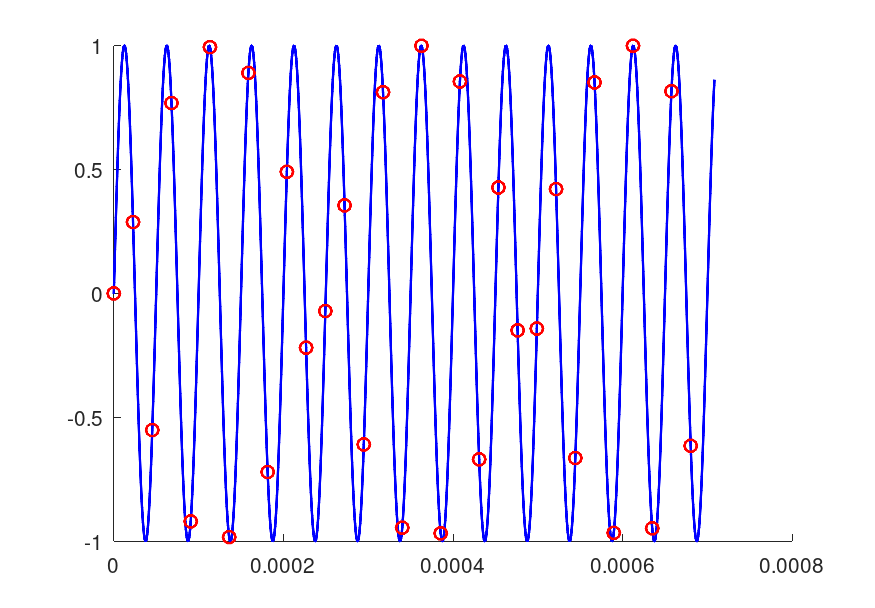
サンプリング点は離散データなのでoctaveのグラフではstemで表示するのが正しいです。
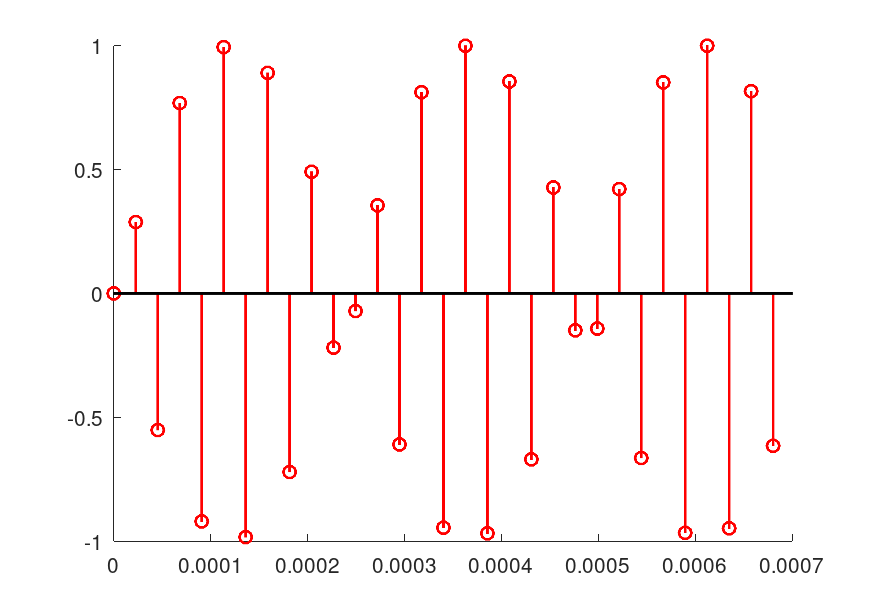
stemで表示したところでこれが20kHzの正弦波には見えません。
なぜ見えないのか?
それはエイリアシングノイズが含まれているからです。
20kHzがfs/2の22050Hzで折り返して24100Hzの成分が加わっているからです。
46100Hzやそれより高い周波数も折返しがありますが、とりあえず一番近いものを考えます。
このように「うなり」が発生します。
20kHzでサンプリング波形が変に見えるのは、サンプリング点が足りないのではなくて「エイリアスが除去できていない」からです。
エイリアスを除去してみます。2倍にアップサンプリングして上記のフィルタを通します。結果を更にアップサンプリングして表示します。

直線位相フィルタの時間遅れはありますが、このように波形が再現できています。
エイリアスがバッチリ見えていますね。
でもこれで良いのです。
ちゃんと原信号の-190dBくらいになってます。
つまり24bitデータでも量子化誤差以下なので無視して良いのです。
20940Hz正弦波
gain が 0.5 なので出力が小さくなって波形が再現できてません。
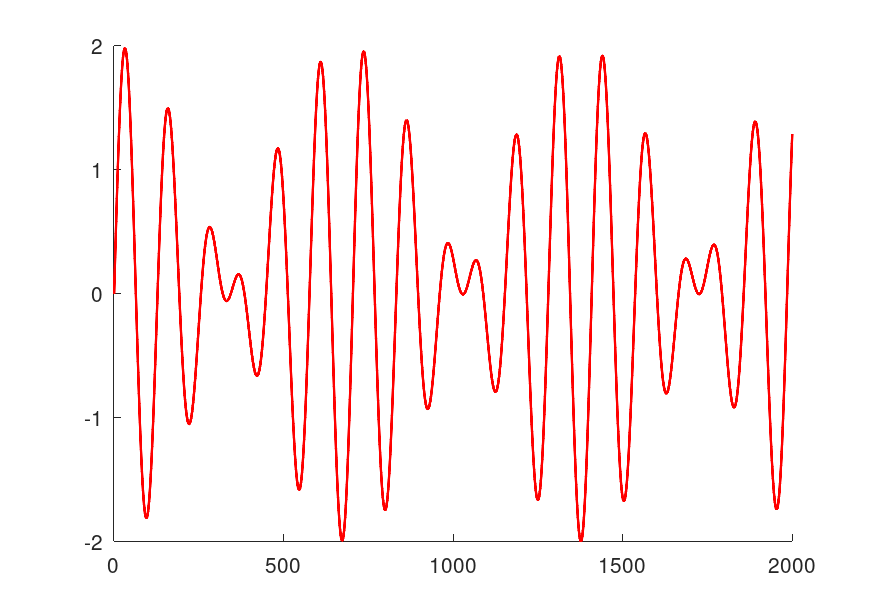
ノイズ波形
正弦波ではなくていろいろな周波数成分を含むノイズ波形を見てみます。
サンプリング定理に従うために21kHzのローパスフィルタに通します。

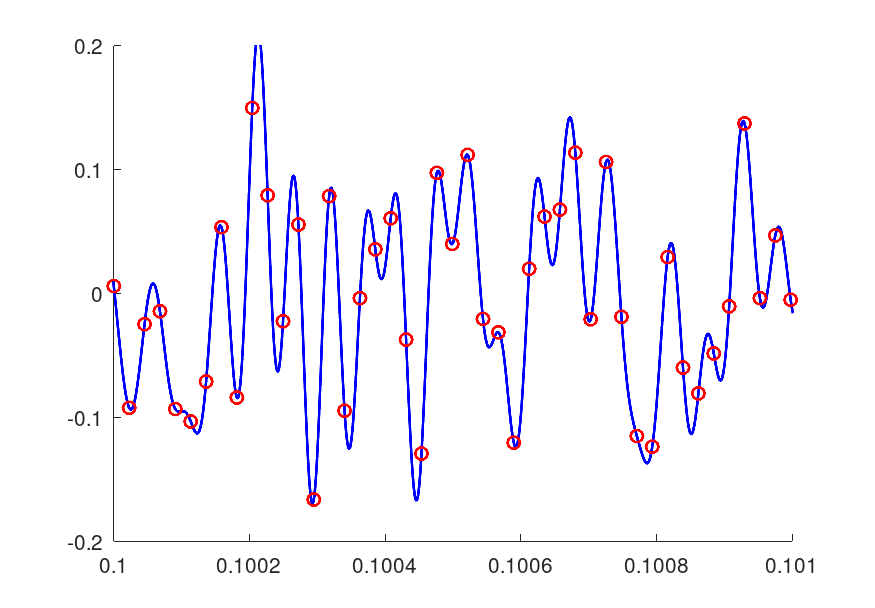
このサンプリング点から波形を再現してみます。
ほぼ波形が再現されています。
微妙に一致しないのは21kHz以上の高域のレベルが落ちているためです。

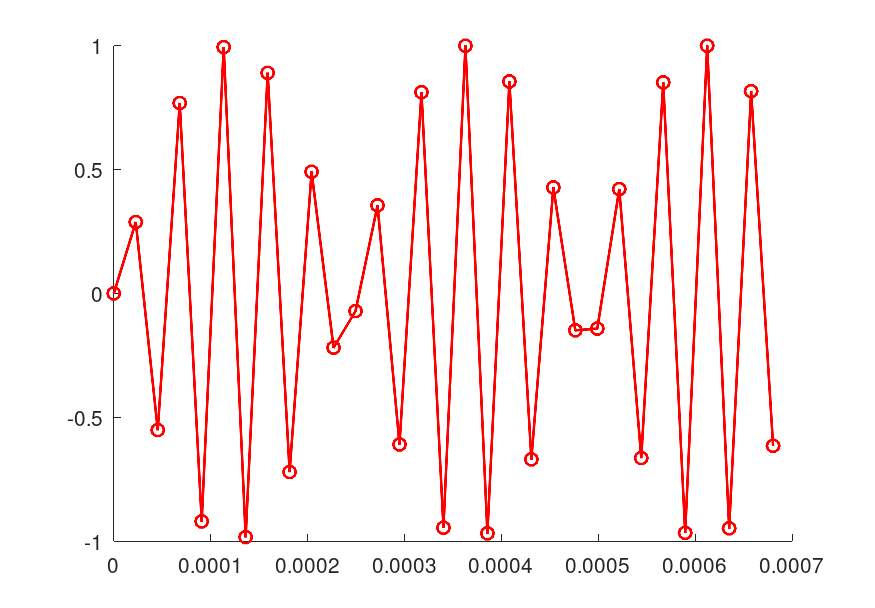
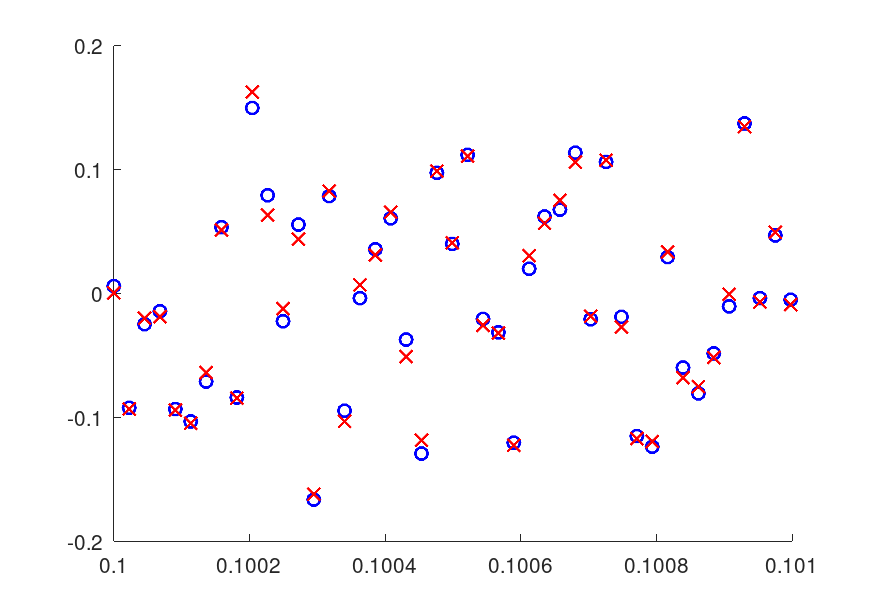
ノイズ波形を1/16サンプルずらしたもの
波形が再現できる、ということはサンプリング間隔よりも小さい時間も再現できるはずです。
サンプリング周波数44100Hzでサンプリング間隔の1/16の時間差を見てみます。
これを見てもなんだかよくわからないのでやはりエイリアスをカットします。
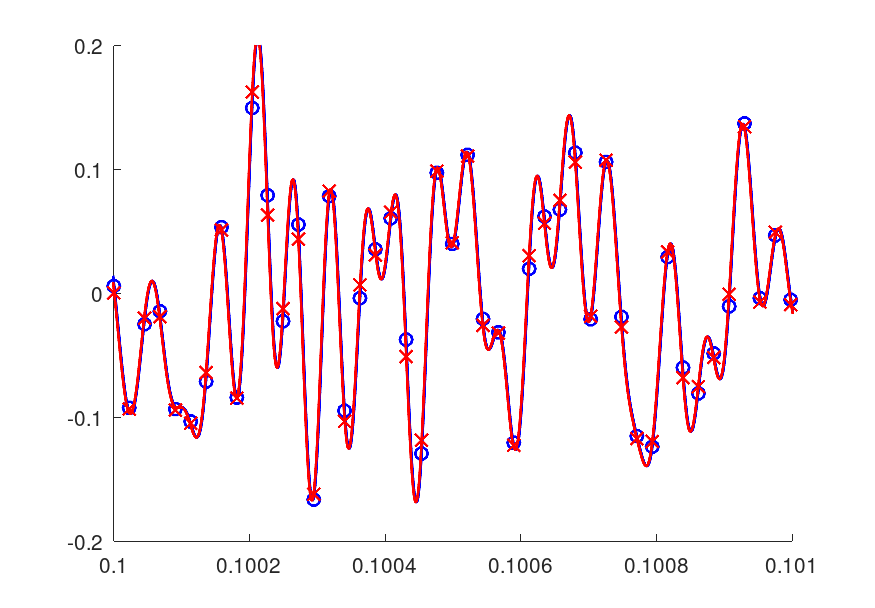
さらに拡大してみる同じ波形が1.42e-06秒ずれて記録されていることがわかります。

このようにサンプリング定理により波形が再現され、サンプリング間隔よりも短い時間差も十分表現できることがわかります。
注:ただしこの時間分解能は使える量子化bit数に依存します。
よくある誤解の間違いを雑に解説する
サンプリング定理は間違ってる、高い周波数になると明らかにサンプル数が足りない!
波形が変なのはサンプル数が足りないのではなく、エイリアスが除去できてないからです。
サンプリング定理は正しいが、無限の長さから補完しなければならないから無理、意味がない
ローパスフィルタに適切な窓関数を使うことにより、現実的な長さのフィルタで十分な特性が得られます。
サンプリング定理によって周波数情報は失われないが波形は再現できない
直線位相の適切なフィルタを使うことにより波形はほぼ完全に再現できます。
サンプリング(離散化)すると時間情報が失われ、サンプリング間隔以下の短い時間差が再現できない
十分な量子化bit数があればサンプリング間隔よりはるかに短い時間差を再現できます。
理想的な処理は無限の長さから補完する必要があるので無理、なら「僕の考えた最強の曲線」で補完してやるぜ!
「僕の考えた最強の曲線」ではまず間違いなくエイリアスを除去しきれません。
それどころか帯域内の特性もフラットになりません。
スプライン曲線も当然ダメです。
帯域内がフラットでエイリアスを除去できるとしたらそれは正しくローパスフィルタです。
おわりに
数式を使わずに(そもそも私が数式を理解してない)サンプリング定理に対する誤解を減らせるように頑張ってみました。
サンプリング定理になるべく忠実な処理を行えば帯域を90%とか95%に妥協することにより十分に波形を再現できることを示しました。
ではなるべくサンプリング定理に忠実な処理をしたほうが良いのか?というと 話は簡単ではありません。
というわけで次回は中編としてサンプリング定理+魑魅魍魎のオーディオ界についてのポエム?となります。