はじめに
こんにちは、麻菜結です。はじめての競技プログラミング解説記事になるのですが、この記事は作問者が思い描いたきれいな解答を咀嚼しながら解説するものではなく、私がコンテスト時間内に半泣き&戸惑いながらACをとってしまった解法を解説する記事となります。
この記事の読者として想定するのは、多かれ少なかれプログラミングを教える立場にある人です。アルゴリズムのコツがつかめないやつってどのあたりでつまずいちゃうんだろうという一例をあげる記事となります。以下見苦しい文章が続きます。よろしくお願いします。
問題文
正の整数A, B, Cが与えられます。A^B^Cの10進法での1の位を求めてください。
AtCoder Regular Contest 113 B A^B^C
思考
じゃあどんなふうに考えようかと言うと、「この解答ってAの1桁目に依存するよな」と考えます。どういうことかというと、例えば5にどんな数をかけようと1桁目は0か5になります、このようにAの1桁目に注目することを思い浮かびます。
さらに、「BとCがどんな数になろうとしょせんはA * A * ...になるからAの1桁目 * Aの1桁目 * ...ででた数字の1桁目にしか解答はありえないよな」となります。さらに踏み込んだ考え方が出来そうですが、愚かにもこのあたりで思考の限界が来てしまい、実装の為の検証に入ります。
検証
検証ですが、0から9までのそれぞれの数字でどのような1桁目になるかを検証するために以下のようなプログラムを組みます。
import sys
A = int(sys.argv[1])
for i in range(1, 10):
for j in range(1, 10):
x = A ** (i ** j)
print(f"LastDigit({A} ** {i} ** {j}) -> {str(x)[-1]}")
もし上のソースコードを実行する方は、コンピュータにそこそこな負荷をかけますのでほどほどな所で[Ctrl]+[C]をしてください。コマンドライン引数から数字を与えた任意の数字AをA^(i^j) [1 <= i,j <= 9]するプログラムです。それぞれを実行すると以下のような傾向が見えてきます。
| 単一の数字しかないもの | 2種類の数字がでるもの | 4種類の数字がでるもの |
|---|---|---|
| 0 → 0 | 4 → 4, 6 | 2 → 2, 4, 6, 8 |
| 1 → 1 | 9 → 1, 9 | 3 → 1, 3, 7, 9 |
| 5 → 5 | 7 → 1, 3, 7, 9 | |
| 6 → 6 | 8 → 2, 4, 6, 8 |
これでとりあえず0, 1, 5, 6なら即断していいのがわかりましたね。 コンピュータの世界は答えさえ合っていれば数学のように証明が無くてもOKなのが楽ですね。
では、数字が2種類でるものを検証しましょう。
$ python exp_test 4
LastDigit(4 ** 1 ** 1) -> 4
LastDigit(4 ** 1 ** 2) -> 4
LastDigit(4 ** 1 ** 3) -> 4
LastDigit(4 ** 1 ** 4) -> 4
LastDigit(4 ** 1 ** 5) -> 4
LastDigit(4 ** 1 ** 6) -> 4
LastDigit(4 ** 1 ** 7) -> 4
LastDigit(4 ** 1 ** 8) -> 4
LastDigit(4 ** 1 ** 9) -> 4
LastDigit(4 ** 2 ** 1) -> 6
LastDigit(4 ** 2 ** 2) -> 6
LastDigit(4 ** 2 ** 3) -> 6
LastDigit(4 ** 2 ** 4) -> 6
LastDigit(4 ** 2 ** 5) -> 6
LastDigit(4 ** 2 ** 6) -> 6
LastDigit(4 ** 2 ** 7) -> 6
LastDigit(4 ** 2 ** 8) -> 6
LastDigit(4 ** 2 ** 9) -> 6
LastDigit(4 ** 3 ** 1) -> 4
LastDigit(4 ** 3 ** 2) -> 4
LastDigit(4 ** 3 ** 3) -> 4
LastDigit(4 ** 3 ** 4) -> 4
LastDigit(4 ** 3 ** 5) -> 4
LastDigit(4 ** 3 ** 6) -> 4
LastDigit(4 ** 3 ** 7) -> 4
LastDigit(4 ** 3 ** 8) -> 4
LastDigit(4 ** 3 ** 9) -> 4
LastDigit(4 ** 4 ** 1) -> 6
LastDigit(4 ** 4 ** 2) -> 6
LastDigit(4 ** 4 ** 3) -> 6
LastDigit(4 ** 4 ** 4) -> 6
LastDigit(4 ** 4 ** 5) -> 6
LastDigit(4 ** 4 ** 6) -> 6
LastDigit(4 ** 4 ** 7) -> 6
LastDigit(4 ** 4 ** 8) -> 6
LastDigit(4 ** 4 ** 9) -> 6
LastDigit(4 ** 5 ** 1) -> 4
LastDigit(4 ** 5 ** 2) -> 4
LastDigit(4 ** 5 ** 3) -> 4
LastDigit(4 ** 5 ** 4) -> 4
LastDigit(4 ** 5 ** 5) -> 4
LastDigit(4 ** 5 ** 6) -> 4
LastDigit(4 ** 5 ** 7) -> 4
LastDigit(4 ** 5 ** 8) -> 4
LastDigit(4 ** 5 ** 9) -> 4
LastDigit(4 ** 6 ** 1) -> 6
LastDigit(4 ** 6 ** 2) -> 6
LastDigit(4 ** 6 ** 3) -> 6
LastDigit(4 ** 6 ** 4) -> 6
LastDigit(4 ** 6 ** 5) -> 6
LastDigit(4 ** 6 ** 6) -> 6
LastDigit(4 ** 6 ** 7) -> 6
^C
長いので折り畳み&途中停止していますが、Bの値が偶数の時は6, 奇数の値の時は4となっており、それが延々と続きそうなのでBが偶数の時と奇数の時で判断できます。書きませんが9の場合は偶数→1, 奇数→9です。
4種類のやつを検証します。
$ python exp_test 2
LastDigit(2 ** 1 ** 1) -> 2
LastDigit(2 ** 1 ** 2) -> 2
LastDigit(2 ** 1 ** 3) -> 2
LastDigit(2 ** 1 ** 4) -> 2
LastDigit(2 ** 1 ** 5) -> 2
LastDigit(2 ** 1 ** 6) -> 2
LastDigit(2 ** 1 ** 7) -> 2
LastDigit(2 ** 1 ** 8) -> 2
LastDigit(2 ** 1 ** 9) -> 2
LastDigit(2 ** 2 ** 1) -> 4
LastDigit(2 ** 2 ** 2) -> 6
LastDigit(2 ** 2 ** 3) -> 6
LastDigit(2 ** 2 ** 4) -> 6
LastDigit(2 ** 2 ** 5) -> 6
LastDigit(2 ** 2 ** 6) -> 6
LastDigit(2 ** 2 ** 7) -> 6
LastDigit(2 ** 2 ** 8) -> 6
LastDigit(2 ** 2 ** 9) -> 6
LastDigit(2 ** 3 ** 1) -> 8
LastDigit(2 ** 3 ** 2) -> 2
LastDigit(2 ** 3 ** 3) -> 8
LastDigit(2 ** 3 ** 4) -> 2
LastDigit(2 ** 3 ** 5) -> 8
LastDigit(2 ** 3 ** 6) -> 2
LastDigit(2 ** 3 ** 7) -> 8
LastDigit(2 ** 3 ** 8) -> 2
LastDigit(2 ** 3 ** 9) -> 8
LastDigit(2 ** 4 ** 1) -> 6
LastDigit(2 ** 4 ** 2) -> 6
LastDigit(2 ** 4 ** 3) -> 6
LastDigit(2 ** 4 ** 4) -> 6
LastDigit(2 ** 4 ** 5) -> 6
LastDigit(2 ** 4 ** 6) -> 6
LastDigit(2 ** 4 ** 7) -> 6
LastDigit(2 ** 4 ** 8) -> 6
LastDigit(2 ** 4 ** 9) -> 6
LastDigit(2 ** 5 ** 1) -> 2
LastDigit(2 ** 5 ** 2) -> 2
LastDigit(2 ** 5 ** 3) -> 2
LastDigit(2 ** 5 ** 4) -> 2
LastDigit(2 ** 5 ** 5) -> 2
LastDigit(2 ** 5 ** 6) -> 2
LastDigit(2 ** 5 ** 7) -> 2
LastDigit(2 ** 5 ** 8) -> 2
LastDigit(2 ** 5 ** 9) -> 2
LastDigit(2 ** 6 ** 1) -> 4
LastDigit(2 ** 6 ** 2) -> 6
LastDigit(2 ** 6 ** 3) -> 6
LastDigit(2 ** 6 ** 4) -> 6
LastDigit(2 ** 6 ** 5) -> 6
LastDigit(2 ** 6 ** 6) -> 6
LastDigit(2 ** 6 ** 7) -> 6
LastDigit(2 ** 6 ** 8) -> 6
LastDigit(2 ** 6 ** 9) -> 6
LastDigit(2 ** 7 ** 1) -> 8
LastDigit(2 ** 7 ** 2) -> 2
LastDigit(2 ** 7 ** 3) -> 8
LastDigit(2 ** 7 ** 4) -> 2
LastDigit(2 ** 7 ** 5) -> 8
LastDigit(2 ** 7 ** 6) -> 2
LastDigit(2 ** 7 ** 7) -> 8
LastDigit(2 ** 7 ** 8) -> 2
^C
難しそうに見えますが、4種類のパターンが続いていくのが推測されます。
| 条件 | パターン |
|---|---|
| B%4 → 1 | X. ある数に定まる(2) |
| B%4 → 2 | Y. 1番目だけ別の数字で後は同じ数字(4, 6) |
| B%4 → 3 | Z. Cが奇数か偶数かによって定まる(2, 8) |
| B%4 → 0 | W. ある数に定まる(6) |
以上は2の場合です。
他の数字は以下のようになります。
| X | Y | Z | W | |
|---|---|---|---|---|
| 3 | 3 | 9,1 | 7,3 | 1 |
| 7 | 7 | 9,1 | 3,7 | 1 |
| 8 | 8 | 4,6 | 2,8 | 6 |
パターンXの場合はA、パターンWの場合はAが偶数の時6、奇数の時1が解答になってますね。さて、そろそろ実装に移っていきますか。
プログラム
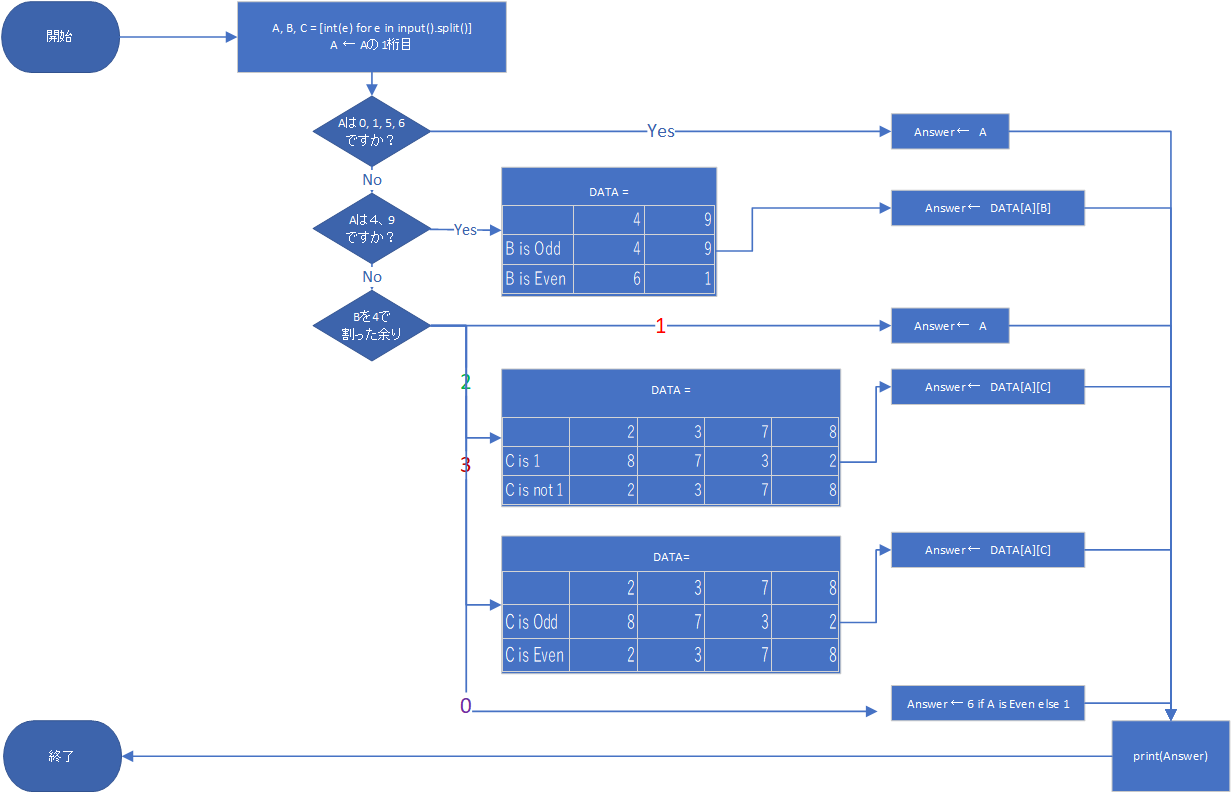
一回整理しましょう。解答はフローチャートっぼくにまとめると以下のようになります。
そして、図とすこし違いますが、解答のプログラムが以下のモノになります。
A, B, C = [int(e) for e in input().split()]
ans = 0
l_A = str(A)[-1]
if(l_A in ["0", "1", "5", "6"]):
ans = {"0":0, "1":1, "5":5, "6":6}[l_A]
elif(l_A in ["4", "9"]):
l_A += "+" if B%2 == 0 else ""
ans = {"4+":6, "9+":1, "4":4, "9":9}[l_A]
elif(B % 4 == 1):
ans = {"2":2, "3":3, "7":7, "8":8}[l_A]
elif(B % 4 == 2):
if(C == 1):
ans = {"2":4, "3":9, "7":9, "8":4}[l_A]
else:
ans = {"2":6, "3":1, "7":1, "8":6}[l_A]
elif(B % 4 == 3):
if(C % 2 == 0):
ans = {"2":2, "3":3, "7":7, "8":8}[l_A]
else:
ans = {"2":8, "3":7, "7":3, "8":2}[l_A]
elif(B % 4 == 0):
ans = {"2":6, "3":1, "7":1, "8":6}[l_A]
print(ans)
おわりに
本当にお疲れさまでした。自分の恥をさらすような記事で、読んでいて「あちゃー」と思っている人もいるかもしれませんが、そうなった人は自分よりもできない人なんかいくらでもいるんだという事実を誇らしく思ってください。
逆に皆さんはどんなふうに競技プログラミングに慣れていきましたか?いつまでも初心者から脱せない感じがモチベをじわじわ削っていく気がします。精進します。最後まで読んでくださってありがとうございました。書きたいネタが出来たらまたかきます。