PyTorch公式チュートリアル Deep Learning with PyTorch #3 Neural Networks

Neural Networks

PyTorchにおけるニューラルネットワークはtorch.nnパッケージを用いて構築することができる。nnはモデルを定義し、微分するためにautogradに依存しており、nn.Moduleが畳み込みニューラルネットワークの畳み込み層、プーリング層、線形結合層などを含んでおり、forward(input)関数が出力を返す。
今回実装したコードのgistはここ

ここでは画像をグレースケール（白黒）画像を分類するフィードフォワードネットワーク¹ を考える。

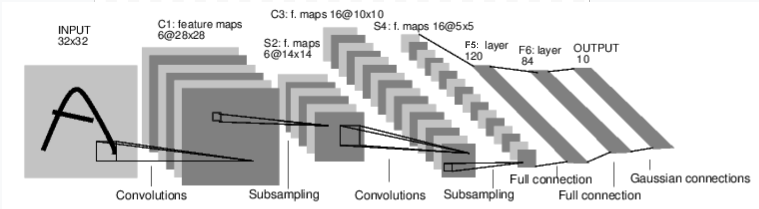
このフィードフォワードニューラルネットワークでは、入力を受け取り、それを複数のレイヤーに次々と伝搬し、最終的に出力を与えるものであり、典型的なニューラルネットワークの手続きは次のようになっている。

• 学習可能なパラメータ($Wx + b$のウェイト$W$など)を持つニューラルネットワークを定義する。
• 入力されたデータセットを繰り返し処理する。
• 入力をネットワークで処理する。
• 実際の正解とネットワークの出力結果の差分であるロスを計算する。
• 勾配をネットワークのパラメータに逆伝搬する。
• ネットワークのウェイトを更新する。この時の更新は以下のような式にそっって行われることが一般的である。

weight = weight - learning_rate * gradient

Define the network

まずネットワークを定義する。今回は二つの畳み込み層を持つConvolutional Neural Networkを実装する。

nn.Conv2dは二次元の畳み込み層であり、in_channels(入力のチャネルサイズ、RGBであれば3、グレースケールであれば1)、out_channels(出力のチャネル数)、kernel_size(スライドさせるウィンドウの大きさ)を渡す。
今回使用した最大プーリング(max pooling)では、ある特定の大きさのストライドを設定し、そのストライド範囲に含まれるノードからの入力のうち最大のものを出力とする²。max_pool2dはnn.functionalで定義されている。

import torch
# autograd, nn など必要なクラス・モジュールを読み込む
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # チャネル数が1、カーネル数が6、ウィンドウサイズが5x5の畳み込み層を定義
        self.conv1 = nn.Conv2d(1, 6, 5)
        # チャネル数が6、カーネル数が16、ウィンドウサイズが5x5の畳み込み層を定義
        self.conv2 = nn.Conv2d(6, 16, 5)
        
        # 入力の次元が16x5x5、出力の次元数が120次元の線形結合層を定義
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        # 入力の次元が120、出力の次元数が84次元の線形結合層を定義
        self.fc2 = nn.Linear(120, 84)
        # 入力の次元が84、出力の次元数が10次元の線形結合層を定義
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # プーリング層を定義。ここではマックスプーリングを用いる
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        # tensorをリサイズする
        x = x.view(-1, self.num_flat_features(x))
        # 線形結合した結果をReLUで活性化する
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        # 最終的な出力結果を計算する
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]
        num_features = 1

        for s in size:
            num_features *= s
        return num_features
net = Net()
print(net)

netを出力すると、定義したようなネットワークが実際に構成されていることが確認できる。
forwardネットワークの定義が完了したため、勾配を計算するbackwardについてはautogradを用いいることにより、自動的に定義ができる。forward関数の全てのTensor操作が利用可能である。学習可能なパラメータはnet.parameters()で定義できる。

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

パラメータを取得する

ネットワークのパラメータについてはnet.parameters()で取得できる。parametersはVariableのサブクラスとなっている。

params = list(net.parameters())
# 出力の大きさが10次元なのでlen(params)=10
print(len(params))
# params[0]はsizeが[6, 1, 5, 5]のtensor
print(params[0].size())

ネットワークにデータを入力する

実際にこのネットワークに何らかの入力を入れた場合の挙動を確認する。ネットワークの入力及び出力はautograd.Variableである。今回は1枚の入力データ、1チャネル

input = Variable(torch.randn(1, 1, 32, 32))
out = net(input)
print(out)
net.zero_grad()
out.backward(torch.rand(1, 10))

backward()関数は勾配を追跡するため、ミニバッチ間で勾配を混ぜてしまうことがないよう、ミニバッチの開始時に勾配をぜろにする必要があり、これをzero_grad()で行うのが一般的である。

Recap

• tourch.Tensor - 多次元配列。Numpyのndarray
• autograd.Variable- Tensorクラスをラップしており、Tensorに適用された演算を記録しており、Tensorクラスの演算に加えてbackward()を可能。
• nn.Module - ニューラルネットワークモジュール。パラメータをカプセル化する。
• nn.Parameter-Variableクラスようなものであり、moduleのあトリビュートとしてアサインされた時にparameterとして登録される。
• autograd.Functionーforward, backwardの定義を行う。全てのVariable演算はFunctionノードを生成する。

Loss Function(損失関数)

loss function（損失関数）はネットワークの出力(output)と正解データ(target)を入力として受け取り、実際の正解から予測結果ががどれほどずれているかを見積もる。
nnパッケージ下には様々な損失関数が定義されている。nn.MSELossはバッチサイズ$N$の際、この$N$個の入力データに対して、ネットワークからの出力$\hat{y_i}$と実際の正解ラベル$y_i$の平均二乗誤差を計算する。
$$MSE~Loss(\hat{y}, y) = ({\hat{y_i} - y_i})^2$$

input = Variable(torch.randn(1, 1, 32, 32))
output = net(input)
target = Variable(torch.arange(1, 11))  # a dummy target, for example
target = Variable.view(1, -1)
criterion = nn.MSELoss()
loss = criterion(output, target)
print(loss) # Variable containing 38.3008 [torch.FloatTensor of size 1]

loss.backward()を呼ぶと、グラフ全体がlossに対して微分され、全てのグラフのVariableは.grad変数を持つ。

Backprop(逆伝播)

loss.backward()を行うだけで誤差を逆伝播できる。すでに存在する勾配を消去する必要があり、これを行わない場合、勾配は蓄積されることになる。
loss.backward()を行うと、convv1のバイアスの勾配が逆伝播の前後で更新される。

Update the weights(重みを更新する)

ウェイトを更新するもっともシンプルな方法の一つにSGDがあり、以下の更新規則にしたがう。

weight = weight - learning_raet * gradient

SGDは以下のように簡単に実装が可能である。

learning_rate = 0.01
for i in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

PyTorchのtorch.optimパッケージは様々なオプティマイザを用意している。

import torch.optim as optim

optimier = optim.SGD(net.parameters(), lr=0.01)
optimer.zero_grad()
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step() # Update

1. フィードフォワードネットワークとは、データの流れが一方こうであり、データが行ったり来たり、あるいはループしたりしないような構造となったニューラルネットワークである。フィードフォワードニューラルネットワークの基本 ↩

2. 深層学習 Deep Learning (監修:人工知能学会) ↩