LoginSignup
70
59

More than 3 years have passed since last update.

@as_kuyain株式会社ディー・エヌ・エー

JavaScriptとWebAudioでサウンド・イコライザーを作る

Last updated at Posted at 2019-08-31

はじめに

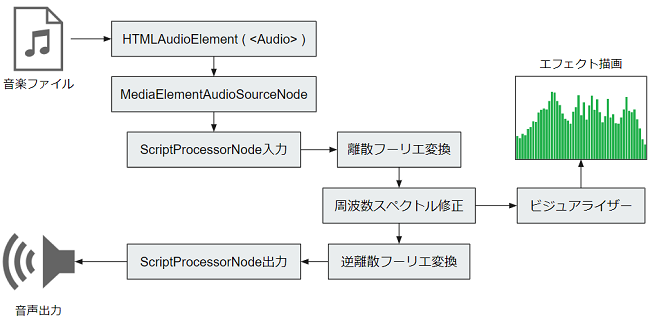
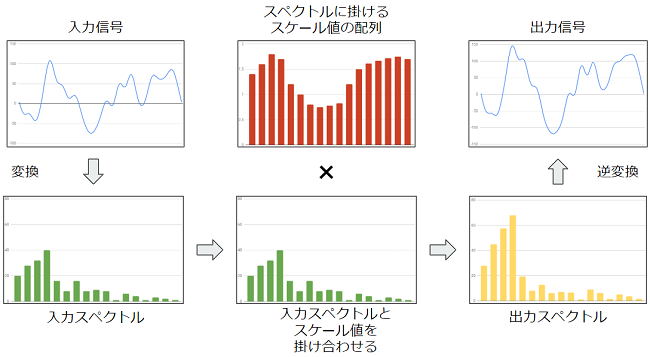
JavaScriptで高速フーリエ変換を実装し、WebAudio上で任意の音声ファイルからデコードした波形データに対し高速フーリエ変換を用いて周波数スペクトルに変換、そして、その周波数スペクトルをリアルタイムに修正し、そのデータを再び波形データに戻し周波数特性を変化させた音をスピーカーから出力出来るパラメトリック・イコライザーを実装してみました。

ついでに高速フーリエ変換から得られる周波数スペクトルのデータを再利用しビジュアライザーも実装しています。

アプリケーションのスクリーンショット

この記事では音声信号に対する高速フーリエ変換の特性と実装方法を主眼に解説を行っていきたいと思います。

設計概要

概要設計図

動作の流れ

  1. 音声ファイルを波形データにデコードする。
  2. 波形データに対して離散フーリエ変換をかけて周波数スペクトルにデータを変換する。
  3. 周波数スペクトルの各周波数に各々のスケール値をかける。
  4. 編集された周波数スペクトルを逆離散フーリエ変換をかけて波形データに戻す。
  5. 波形データをスピーカーに出力する。
  6. 上記の処理で得られた周波数スペクトルのデータを流用してWebGLによりビジュアライザーの描画を行う。

上記の動作をリアルタイムに且つ連続的を行います。

実装部分

  • 操作UI
    • 音声ファイル選択用UIの実装
    • 音声の再生、停止用UIの実装
    • イコライザ用UIの実装
  • 音声処理
    • 音声ファイルの読み込み処理の実装
    • 波形データの取り込み処理の実装
    • 波形データの出力処理の実装
  • 信号処理
    • 高速フーリエ変換の実装
    • 周波数スペクトルのスケーリングの実装
  • ビジュアライザ
    • 3Dビジュアライザーの描画の実装

このアプリケーションのポイント

このアプリケーションでは周波数解析のみならず、解析データを修正し、再び周波数特性の変更された波形データに戻しスピーカーから鳴らすところにあります。周波数解析を行いビジュアライザーだけを実装したいのであればAnalyserNodeを用いれば周波数スペクトルは取得出来、ビジュアライザーを作る事も出来ます。

しかしAnalyserNodeは音圧情報しか取得出来ず、離散フーリエ変換では取得できる各周波数の位相情報が取得出来ず、AnalyserNodeで取得出来るデータに無理やり逆離散フーリエ変換をかけても視聴に耐えうる波形データには戻りません。

このアプリケーションのポイントは音声を解析し、修正し、周波数特性を編集した音声データとしてスピーカーに出力できることに意義があります。

離散フーリエ変換（Discrete Fourier Transform : DFT）

概要

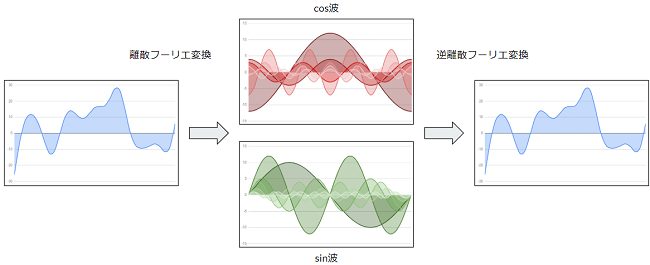
離散フーリエ変換（Discrete Fourier Transform : DFT）とは簡単に言うとN個の離散信号に対しN個の周波数の異なる単純なcos波とsin波の組に分解することの出来る変換です。

波形データを三角関数に分解

N個の離散信号に対し離散フーリエ変換を行うと、その解は 0Hz, 1Hz, 2Hz, 3Hz, ... (N/2 - 1)Hz, N/2Hz と正の周波数の情報が配列され、そして後半は折り返して -(N/2 - 1)Hz, -(N/2 - 2), ..., -3Hz, -2Hz, -1Hz と負の周波数の情報が配列されます。

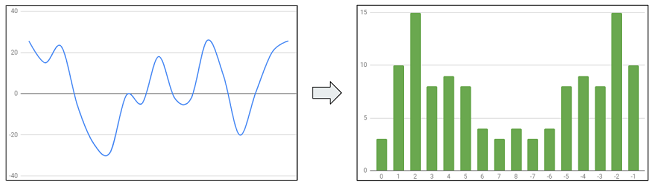
周波数スペクトル

実際に波形データに適用する場合は一定区間、例えば1024サンプル等のプロックで区切り、そのデータに対し離散フーリエ変換を行い波形データの周波数特性の解析を行います。そして、その周波数スペクトルに対しイコライザーなら編集を行い、ビジュアライザーなら描画に利用したりします。

周波数スペクトルのスケーリング

例えば上の図のようにスケール値をかけて低音を強く、中音を弱く、高音を強くする変換をかけることにより言わいるドンシャリ系の音を作る事もできます。

正変換

数式

y_k=\sum_{j=0}^{N-1}x_j e^\frac{-2iπjk}{N}, k=0,1,...,N-1
  • x - 入力される信号の配列
  • j - 入力される信号の配列インデックス
  • y - 出力される周波数スペクトルの配列
  • k - 出力される周波数スペクトルの配列インデックス
  • N - 離散信号の個数
  • i - 単位虚数
実装例
/**
 * 離散フーリエ変換
 * @param n 変換するデータの要素数
 * @param a 入力用のデータ、実数、虚数の順で配置する必要がある
 * @param b 出力用のデータ、実数、虚数の順で配列される
 */
static dft(n, a, b) {
    // b[k] = Σ[N - 1, j = 0] a[j] * e^(-2.0 * π * i * j * k / N)
    for (let k = 0; k < n; ++k) {
        // Σ[N - 1, j = 0] a[j] * e^(-2.0 * π * i * j * k / N)
        let sumRe = 0;
        let sumIm = 0;
        for (let j = 0; j < n; ++j) {
            // e^(-2.0 * π * i * j * k / N)
            let rad = -2.0 * Math.PI * k * j / n;
            let cs = Math.cos(rad), sn = Math.sin(rad);
            let re = a[(j << 1) + 0], im = a[(j << 1) + 1];
            // a[j] * e^(-2.0 * π * i * j * k / N)
            sumRe += re * cs - im * sn;
            sumIm += re * sn + im * cs;
        }
        b[(k << 1) + 0] = sumRe;
        b[(k << 1) + 1] = sumIm;
    }
}

逆変換

x_j=\frac{1}{N}\sum_{k=0}^{N-1}y_k e^\frac{2iπjk}{N}, j=0,1,...,N-1
  • x - 出力される信号の配列
  • j - 出力される信号の配列インデックス
  • y - 入力される周波数スペクトルの配列
  • k - 入力される周波数スペクトルの配列インデックス
  • N - 離散信号の個数
  • i - 単位虚数

実装例

/**
 * 逆離散フーリエ変換
 * @param n 変換するデータの要素数
 * @param a 入力用のデータ、実数、虚数の順で配置する必要がある
 * @param b 出力用のデータ、実数、虚数の順で配列される
 */
static idft(n, a, b) {
    // b[j] = Σ[N - 1, k = 0] (1 / N) * a[k] * e^(2.0 * π * i * j * k / N)
    for (let j = 0; j < n; ++j) {
        // Σ[N - 1, k = 0] (1 / N) * a[k] * e^(2.0 * π * i * j * k / N)
        let sumRe = 0;
        let sumIm = 0;
        for (let k = 0; k < n; ++k) {
            // e^(2.0 * π * i * j * k / N)
            let rad = 2.0 * Math.PI * j * k / n;
            let cs = Math.cos(rad), sn = Math.sin(rad);
            let re = a[(k << 1) + 0], im = a[(k << 1) + 1];
            // a[k] * e^(2.0 * π * i * j * k / N)
            sumRe += re * cs - im * sn;
            sumIm += re * sn + im * cs;
        }
        b[(j << 1) + 0] = sumRe / n;
        b[(j << 1) + 1] = sumIm / n;
    }
}

使用例

let a = [ 10, 2, 4, 3, 1, -1, -4, 2, 3, -9, 20, 12, -30, 15, -13, -20 ];
let b = new Array(16);
let c = new Array(16);

// 正変換
DFT.dft(8, a, b);

// 逆変換
DFT.idft(8, b, c);

計算量について

高速化されていない素直に実装された離散フーリエ変換の計算量は N * N のオーダーで増加します。つまり、計算するサンプル数を2倍にすると計算量は4倍、計算するサンプル数を4倍にすると16倍とサンプル数を増やすと飛躍的に計算量が増します。

音声信号に対する離散フーリエ変換の特性

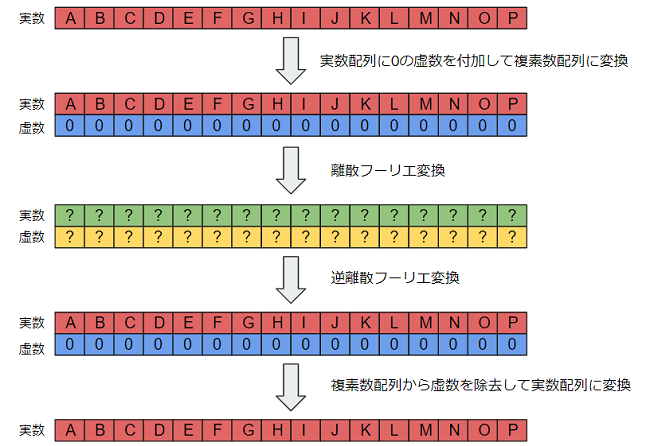
実数配列から複素数（2次元ベクトル）配列への変換

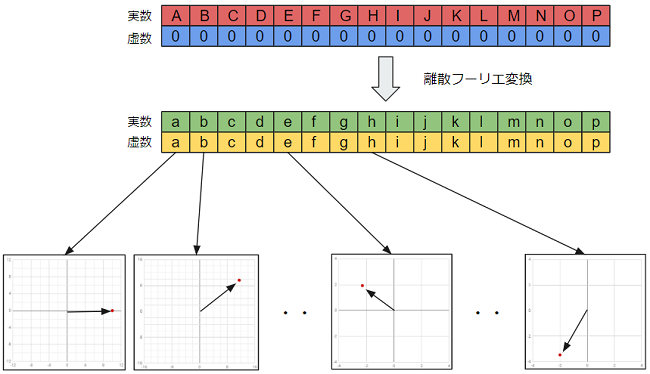
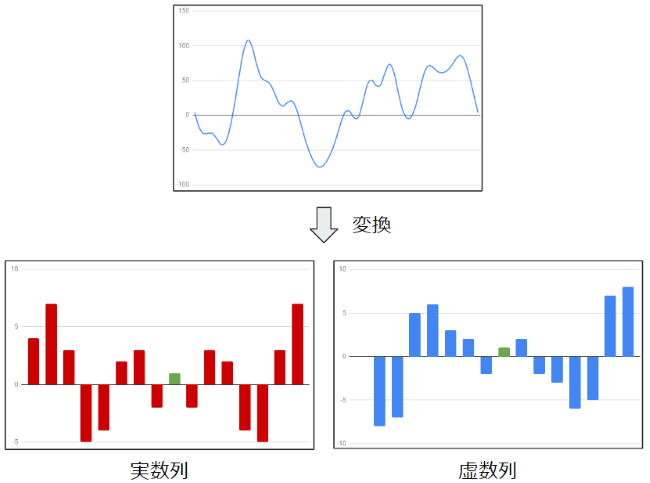
離散フーリエ変換は入力と出力の値が実数と虚数の組、つまり複素数（2次元ベクトル）の配列となり実数（1次元ベクトル）の配列である音声の波形データに対し直接、離散フーリエ変換をかけることが出来ません。

そこで、音声の波形データに対して実数に波形データの値を詰め、虚数には0を詰め、複素数に変換した上で離散フーリエ変換をかける必要があります。そして逆変換時は複素数配列から実数部を取り出し、虚数部を捨て実数配列に変換を行います。

実数配列への離散フーリエ変換を適用

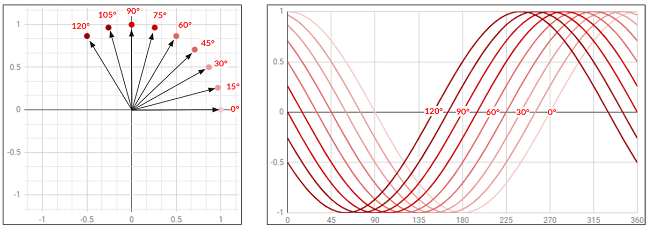
この複素数の2次元ベクトルの実数部にはcos波の振幅の大きさ、虚数部にはsin波の振幅の大きさのが入り、更に直行座標系で表すことが可能で、ベクトルの絶対値（長さ）と偏角に各周波数の特徴が保持されています。

複素数配列の2次元ベクトル

この図ではX軸が実数（cos波の振幅の大きさ）、Y軸を虚数（sin波の振幅の大きさ）として表しています。

絶対値

各周波数の複素数の絶対値（長さ）は実数部の2乗と虚数部の2乗を足し合わせた平方根となります。この絶対値が各周波数の音量となります。

|X|=\sqrt{Re^2 + Im^2}

絶対値の意味合い

つまり、各周波数の絶対値に対して任意のスケール値を掛け、再び逆離散フーリエ変換で波形データに戻す事によりパラメトリック・イコライザーを実装する事が出来ると言うわけです。

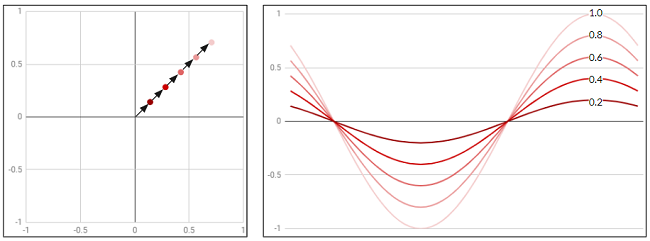
偏角

各周波数の複素数（2次元ベクトル）が複素数平面の実数軸から何度ずれているか。これが偏角となり、この偏角が0°、絶対値が1なら逆変換したときはcos波が得られ、45°ならcos波が1/√2倍されたものとsin波が1/√2倍されたものが足し合わされた波が得られ、90°ならsin波が得られ、180°ならcos波を反転したものが得られ、-90°ならsin波を反転したものが得られます。

この偏角はcos波の位相差を表していると考える事が出来ます。

偏角の意味合い

この偏角に関しては今回の実装で位相は修正しませんが、この値もまた音声の性質を表す重要な情報となります。この性質をうまく利用するとリバーブやインパルス応答や応用した立体音響等を実装することが出来たりします。

それとAnalyserNodeで音声を解析した際には各周波数の絶対値は得られるのですが、この偏角の情報が欠落するのでAnalyserNodeの情報はパラメトリック・イコライザーでは使用できない理由となります。

音声の波形データに対する離散フーリエ変換の解の特性

離散フーリエ変換は本来、複素数配列に適用する変換であり音声のような実数配列に対して適用する変換ではありません。それ故に実数のみに数値の入ったデータに対して離散フーリエ変換を行うと少し変わった解が得られます。

N個の離散データに対して離散フーリエ変換を行うと0からN/2番目までのデータは正の周波数のデータが入るわけですが、それ以降の負の周波数列には正の周波数のデータを鏡写しにコピーしたかのようなデータが入ります。

具体的には整数列は文字通りN/2番目を中心に数値を偶関数のような鏡写しにしたデータが入り虚数列にはN/2を中心に符号を反転させた数値が奇関数のような鏡写しにしたデータが入ります。

音声に対するDFTの特性

実は音声の波形データに対する離散フーリエ変換では意味のあるデータはN/2番目までであり、それ以降のデータはあまり重要なデータではなくN/2以前のデータで復元出来るデータとなります。

高速フーリエ変換（Fast Fourier transform : FFT）

離散フーリエ変換の計算量はN^2のオーダーで増加していきます。例えば128サンプルを処理する場合を基準に考えた場合、256サンプルを処理する場合と比較して計算量は4倍、512サンプルを処理する場合は16倍、1024サンプルを処理する場合は64倍と処理するサンプル数を増やすと飛躍的に計算量が増加します。

そこで離散フーリエ変換の処理負荷を減らすために高速化を考えなければなりません。そして考案された離散フーリエ変換を高速化するアルゴリズム、これらを総称して高速フーリエ変換（Fast Fourier transform : FFT）と呼びます。何種類かあるのですが、どのアルゴリズムでも概ねN log Nの計算オーダーで処理を行うことが出来ます。

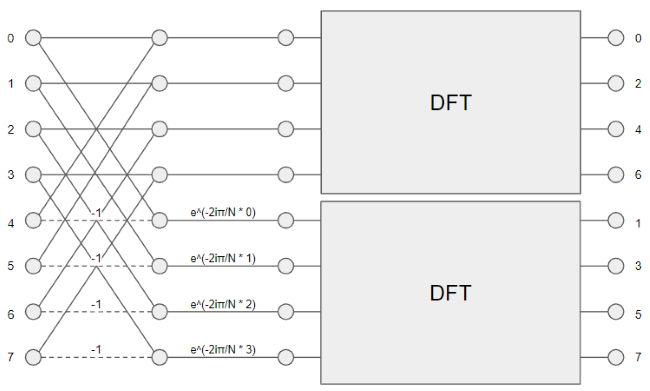
Cooly-Tuky型FFT

高速フーリエ変換の有名なアルゴリズムとしてCooly-Tuky型FFTと呼ばれるものがあります。基本原理としては離散フーリエ変換をより小さな単位に再帰的に問題を分解することにより高速化を行います。結果としてN log Nの計算オーダーで計算できるアルゴリズムとなります。

例えば1024サンプルの波形データを処理する場合を考えた場合、高速化されていない離散フーリエ変換と比べCooly-Tuky型FFTは論理的には1/100程度のオーダーで処理をすることが出来ます。

数式

Cooly-Tuky型FFTには幾つか処理方法が存在しますが最も考え方が簡単であろう方法を紹介します。

y_{2k}=\sum^{\frac{N}{2}-1}_{j=0}(x_j+x_{\frac{N}{2}-j})e^{\frac{-4iπjk}{N}}\\
y_{2k+1}=\sum^{\frac{N}{2}-1}_{j=0}((x_j+x_{\frac{N}{2}-j})e^{\frac{-2iπj}{N}})e^{\frac{-4iπjk}{N}}

考え方としてはデータに前処理を施し偶数列と奇数列に分割し、それぞれの配列でN/2の離散フーリエ変換を行う方法になります。この数式の通り実装を行うと前処理を除き、計算量は2分の1になります。

高速フーリエ変換

そして、この処理は再帰的に行うことが行うことが出来ます。

例えば1024サンプルに対し、このアルゴリズムを再帰的に適用した場合は 1024 -> 512 -> 256 -> 128 -> 64 -> 32 -> 16 -> 8 -> 4 -> 2 と行った感じで、より小さい単位に離散フーリエ変換に分割されます。

実装例

基本型

高速フーリエ変換の基本的な考え方を単純に直線的に実装したものになります。

/**
 * 高速フーリエ変換、単純な再帰呼び出しを使用した実装
 * @param n 変換するデータの要素数、実装の特性上2のべき乗を指定する必要がある
 * @param v 変換するデータ、実数、虚数の順で配置された複素数の配列
 * @param inv 逆変換を行う場合は true を設定する
 * @param off 変換を行う配列vの配列インデックス
 */
static simpleFFT(n, v, inv = false, off = 0) {
    // 前処理
    let rad = (inv ? Math.PI : -Math.PI) / n;
    for (let j = 0; j < n; j += 2) {
        let a = off + j;
        let ar = v[a + 0], ai = v[a + 1];
        let b = off + n + j;
        let br = v[b + 0], bi = v[b + 1];

        // 偶数列 (a + b)
        v[a + 0] = ar + br;
        v[a + 1] = ai + bi;

        // 奇数列 (a - b) * w
        let xr = ar - br, xi = ai - bi;
        let r = rad * j;
        let wr = Math.cos(r), wi = Math.sin(r); // 回転因子 e^(-2 * π * i * j / N)
        v[b + 0] = xr * wr - xi * wi;
        v[b + 1] = xr * wi + xi * wr;
    }

    // 再帰的にDFTをかける
    let nd = n << 1;
    if (n > 2) {
        DFT.simpleFFT(n >>> 1, v, inv, off); // 偶数列
        DFT.simpleFFT(n >>> 1, v, inv, off + n); // 奇数列

        // 並べ替え
        for (let m = nd, mh = n, mq; 1 < (mq = mh >>> 1); m = mh, mh = mq) {
            for (let i = mq; i < nd - mh; i += m) {
                for (let j = i, k = i + mq; j < i + mq; j += 2, k += 2) {
                    DFT.swap(v, off + j, off + k);
                }
            }
        }
    }

    // 逆変換用のスケール
    if (inv) {
        DFT.scaleElements(nd, v, 2, off);
    }
}

Windows10, Intel Core i7-8700K, Google Chromeの環境でざっくりパフォーマンス計測してみたところ1024サンプルの変換の場合、高速化されていない離散フーリエ変換と比べてみたところ300倍程の高速化する事が出来ました。

使用例
let a = [ 10, 2, 4, 3, 1, -1, -4, 2, 3, -9, 20, 12, -30, 15, -13, -20 ];

// 正変換
DFT.simpleFFT(8, a);

// 逆変換
DFT.simpleFFT(8, a, true);

発展型

基本的な高速フーリエ変換の実装に対し再帰呼び出しの排除を行い実装の最適化を図った実装となります。

/**
 * 高速フーリエ変換
 * @param n 変換するデータの要素数、実装の特性上2のべき乗を指定する必要がある
 * @param v 変換するデータ、実数、虚数の順で配置された複素数の配列
 * @param inv 逆変換を行う場合は true を設定する
 */
static fft(n, v, inv = false) {
    let rad = (inv ? 2.0 : -2.0) * Math.PI / n;
    let nd = n << 1;

    for (let m = nd, mh; 2 <= (mh = m >>> 1); m = mh) {
        for (let i = 0; i < mh; i += 2) {
            let rd = rad * (i >> 1);
            let cs = Math.cos(rd), sn = Math.sin(rd); // 回転因子

            for (let j = i; j < nd; j += m) {
                let k = j + mh;
                let ar = v[j + DFT.RE], ai = v[j + DFT.IM];
                let br = v[k + DFT.RE], bi = v[k + DFT.IM];

                // 前半 (a + b)
                v[j + DFT.RE] = ar + br;
                v[j + DFT.IM] = ai + bi;

                // 後半 (a - b) * w
                let xr = ar - br;
                let xi = ai - bi;
                v[k + DFT.RE] = xr * cs - xi * sn;
                v[k + DFT.IM] = xr * sn + xi * cs;
            }
        }
        rad *= 2;
    }

    // 要素の入れ替え
    DFT.swapElements(n, v);

    // 逆変換用のスケール
    if (inv) {
        DFT.scaleElements(nd, v, n);
    }
}

こちらも前項と同じ環境でパフォーマンス計測してみたところ1024サンプルの場合、基本型の実装の4倍程度、高速化なしの実装の1000倍程度の高速化が出来ました。

変則型

少し蛇足にはなるのですが、もう少し高速化を考えてみます。

前項の発展型の高速フーリエ変換のアルゴリズムの回転因子の周期性に着目し、計算精度を少々犠牲にしてMath.cos, Math.sinの呼び出し回数を複素数同士の演算でそれを代替することで、2(N-1)回の三角関数の呼び出し回数を2回までに抑えた実装になります。

/**
 * 高速フーリエ変換、精度を多少犠牲にして速度を向上させたタイプ。
 * @param n 変換するデータの要素数、実装の特性上2のべき乗を指定する必要がある。
 * @param v 変換するデータ、実数、虚数の順で配置された複素数の配列。
 * @param inv 逆変換を行う場合は true を設定する。
 */
static fftHighSpeed(n, v, inv = false) {
    let rad = (inv ? 2.0 : -2.0) * Math.PI / n;
    let cs = Math.cos(rad), sn = Math.sin(rad); // 回転因子の回転用複素数
    let nd = n << 1;

    for (let m = nd, mh; 2 <= (mh = m >>> 1); m = mh) {
        // 回転因子が0°の箇所を処理
        for (let i = 0; i < nd; i += m) {
            let j = i + mh;
            let ar = v[i + DFT.RE], ai = v[i + DFT.IM];
            let br = v[j + DFT.RE], bi = v[j + DFT.IM];

            // 前半 (a + b)
            v[i + DFT.RE] = ar + br;
            v[i + DFT.IM] = ai + bi;

            // 後半 (a - b)
            v[j + DFT.RE] = ar - br;
            v[j + DFT.IM] = ai - bi;
        }

        // 回転因子が0°以外の箇所を処理
        let wcs = cs, wsn = sn; // 回転因子
        for (let i = 2; i < mh; i += 2) {
            for (let j = i; j < nd; j += m) {
                let k = j + mh;
                let ar = v[j + DFT.RE], ai = v[j + DFT.IM];
                let br = v[k + DFT.RE], bi = v[k + DFT.IM];

                // 前半 (a + b)
                v[j + DFT.RE] = ar + br;
                v[j + DFT.IM] = ai + bi;

                // 後半 (a - b) * w
                let xr = ar - br;
                let xi = ai - bi;
                v[k + DFT.RE] = xr * wcs - xi * wsn;
                v[k + DFT.IM] = xr * wsn + xi * wcs;
            }

            // 回転因子を回転
            let tcs = wcs * cs - wsn * sn;
            wsn = wcs * sn + wsn * cs;
            wcs = tcs;
        }

        // 回転因子の回転用の複素数を自乗して回転
        let tcs = cs * cs - sn * sn;
        sn = 2.0 * (cs * sn);
        cs = tcs;
    }

    // 要素の入れ替え
    DFT.swapElements(n, v);

    // 逆変換用のスケール
    if (inv) {
        DFT.scaleElements(nd, v, n);
    }
}

この実装も同じ環境でパフォーマンス計測してみたところ1024サンプルの場合、基本型の実装の10倍程度、発展型の実装の2.5倍、高速化なしの実装と比べ実に4000程度倍ほど高速化出来ました。

音声の波形データに高速フーリエ変換を適用する

音声ファイルから波形データを取り出す

音声ファイルから波形データを取り出し、そのデータに対し高速フーリエ変換でデータを処理するための下地をつくります。

// Audio関連の初期化
function initAudio() {
    // AudioContextを生成
    audioContext = new AudioContext();

    // ScriptProcessorNodeを生成
    scriptProcessor = audioContext.createScriptProcessor(NUM_SAMPLES, 2, 2);
    scriptProcessor.addEventListener("audioprocess", onAudioProcess); // 波形データを処理するメソッドを指定
    scriptProcessor.connect(audioContext.destination); // スピーカーを出力先に設定

    // HTMLAudioElement (<audio>タグ) を生成
    audioElement = new Audio();
    audioElement.loop = true;
    audioElement.autoplay = true;
    audioElement.url = "music.wav"; // 再生したい曲を設定

    // MediaElementAudioSourceNodeを生成
    audioSource = audioContext.createMediaElementSource(audioElement); // HTMLAudioElementからデータ受ける
    audioSource.connect(scriptProcessor); // データの出力先をScriptProcessorNodeに設定
}

// 波形データを処理する為のメソッド
function onAudioProcess(event) {
    let input = event.inputBuffer;
    let output = event.outputBuffer;
    for (let i = 0; i < output.numberOfChannels; ++i) {
        let inputData = input.getChannelData(i); // 入力された波形データを読み込む為の配列

        //
        // ここで入力された波形データに離散フーリエ変換を用いて周波数特性行う
        // 

        let outputData = output.getChannelData(i); // 出力する波形データを書き込む為の配列
    }
}

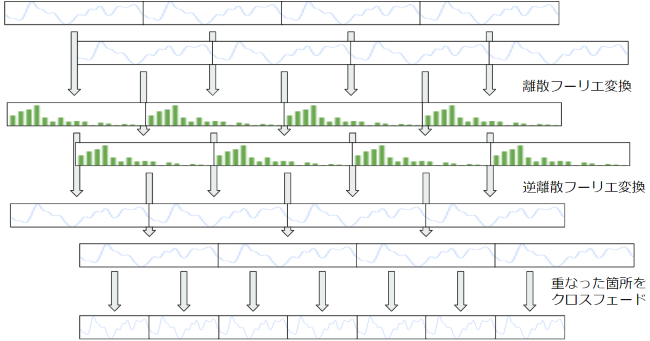
ブロック単位での波形データ処理

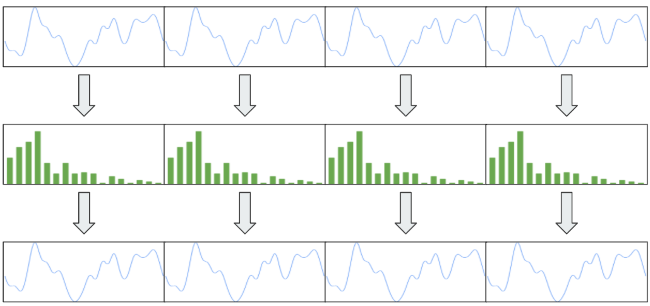
リアルタイムにイコライザーの数値を音声データやビジュアライザに適用するためデータを小分けにして高速フーリエ変換でデータを処理します。レイテンシの事を考えるとおおよそ1024サンプルか2048サンプルを1ブロックとして高速フーリエ変換で周波数解析、加工、再変換、そして出力するのが適当かと思います。

ブロック単位の処理

実装例

// 入力されたデータは実数配列なので複素数配列に変換する
for (let j = 0; j < NUM_SAMPLES; ++j) {
    let index = j * 2;
    audioWorkBuffer[index] = inputData[j];
    audioWorkBuffer[index+ 1] = 0.0; // 虚数部は0で埋める
}

// 離散フーリエ変換を行い周波数スペクトルに変換
DFT.fft(NUM_SAMPLES, audioWorkBuffer);

// 
// 周波数特性を変更する
// 

// 逆フーリエ変換を行い波形データに戻す
DFT.fft(NUM_SAMPLES, audioWorkBuffer, true);

// 処理されたデータは複素数配列なので実数配列に変換する
for (let j = 0; j < NUM_SAMPLES; ++j) {
    outputData[j] = audioWorkBuffer[j * 2]; // 実数部だけ取り出す
}

ブロック同士のクロスフェード

ブロック単位で高速フーリエ変換を行い、そのデータを加工、再変換して音声として出力するとブロックで編集する特性上、ブロックとブロックのつなぎ目で高周波数のノイズが発生します。そのためそれを発生させないようにするためブロック同士を時間的に重ね合わせるように変換を行い、それをクロスフェードさせながら滑らかに接続していきます。

クロスフェード処理

ビジュアライザーを実装する

ついでにはなりますが、パラメトリック・イコライザーのための高速フーリエ変換で計算したデータを流用してビジュアライザーを作成します。

高速フーリエ変換から得られたデータは位相情報を使用せず、絶対値のみを使用する場合はデータの形状は違うもののAnalyserNodeのデータと本質的には同じものになります。

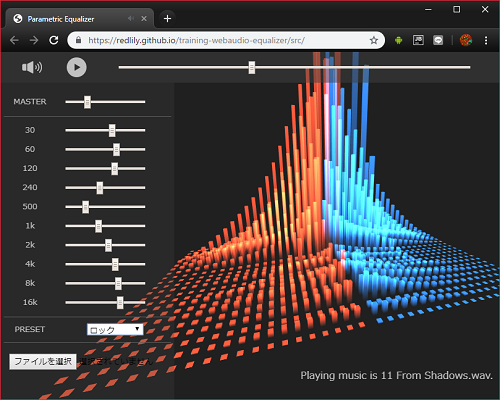
出来上がったもの

Webアプリ

操作方法

  • 三角ボタンで再生、停止
  • 音量のボタンでイコライザの表示非表示
  • イコライザのスライダーで各周波数別の音量変更
  • ファイル選択かドラック・アンド・ドロップで再生する音声ファイルを選択
  • ビジュアライザーはドラッグで回す事が可能

動作環境

  • Chrome (推奨)
  • Firebox
  • Edge
  • Safari
  • Android Chrome（重すぎて不安定）
  • iOS Safari（重すぎて不安定）

JavaScriptで波形データの信号処理と3D描画を同時に行っているのでそれなりに重いです。
もしかしたら古いノートPCのようなスペックが低いマシーンだと音飛びするかもしれません。

参考

70
59
2

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
70
59